正三角形排列剛性耦合三圓柱渦激振動特性及尾渦模式

張曉娜， 及春寧 ,2， 陳威霖， 許 棟,2， 張志猛

(1. 天津大學 水利工程仿真與安全國家重點實驗室，天津 300350；2. 天津大學 中國地震局地震工程綜合模擬與城鄉抗震韌性重點實驗室，天津 300350)

一直以來，圓柱形結構物的渦激振動問題是研究的熱點。圓柱在來流的作用下產生周期性交替瀉渦，在一定條件下，瀉渦誘發的交變流體力會引發圓柱的大振幅響應。對圓柱渦激振動的研究具有非常重要的工程和科學價值[1-4]。其中，對低雷諾數圓柱渦激振動問題的研究，可以提高對以工業熱交換管為代表的小直徑結構物渦激振動的認識，指導優化設計，提高其疲勞壽命。一般來說，工業鍋爐和核反應堆冷卻器的熱交換管直徑較小，且熱媒多為密度較小的水蒸氣，流動的雷諾數較低(～O×102)。此外，熱交換管之間多通過卡具剛性連接，形成陣列。因此，對剛性耦合圓柱陣列的研究具有明顯的應用價值。

對以單圓柱為代表的鈍頭體渦激振動的研究已經持續了幾十年，并取得了大量的成果[5-8]。Williamson等[9-10]通過一系列的實驗研究發現，單圓柱渦激振動的振動響應受質量-阻尼比系數(m*ζ)的顯著影響。當m*ζ較小時，振動響應可分為初始分支，上端分支和下端分支，分別對應 2S(一個振動周期內從圓柱的兩側分別脫落一個旋渦)、2P(一個振動周期從圓柱的兩側分別脫落一對旋渦)和2PO模式三種。需要指出的是，2PO模式的渦對中兩個旋渦的強度不等。當m*ζ較大時，振動響應僅出現初始和下端兩個分支。目前對低雷諾數單圓柱渦激振動的研究表明，不論m*ζ怎么變化，振動響應始終表現為初始和下端兩個分支[11-12]。

在多柱體繞流方面，Bansal 等[13]對間距比L*= 1.35(L*=L/D, 其中L為兩圓柱中心距離，D為圓柱直徑)和雷諾數Re= 2.1×103條件下，入射角度α對等邊三角形布置三圓柱繞流的影響進行了研究，其中α= 0°～60°(α=0°對應一個圓柱位于上游，兩個圓柱在下游并排放置的工況，α=60°對應上游兩個并排圓柱，下游一個圓柱的工況)。發現：所有入射角工況下圓柱間均出現射流，并形成兩個明顯的尾流區—寬尾流和窄尾流，且回流區長度隨α變化。窄尾流中的小尺度旋渦會在圓柱下游融合并形成大尺度旋渦，其脫渦頻率與同等雷諾數下單圓柱繞流相同。Lam等[14-15]通過流場可視化發現，間距比和入射角對靜止三圓柱之間的流動特性有顯著影響。

與多柱體繞流相比，目前對柱群渦激振動的研究則相對較少。對于自由振動(圓柱之間無連接)的情況，Kubo等[16]對不同排列多圓柱風致振動的實驗研究表明，L*= 4.0的等邊三角形布局抑制系統振動最佳。Chen等[17]對L*=1.2～5.0和折合流速Ur= 3～80工況下串列三圓柱的渦激振動數值模擬表明，當L*=1.2時，串列三圓柱振動表現為馳振現象，而當L*= 1.5～5.0時，下游兩圓柱表現為大振幅的渦激振動，上游圓柱的渦激振動隨L*的增加而趨于單圓柱的情況。徐楓等[18]對雷諾數Re= 200工況下的正三角形排列自由振動三圓柱的渦激振動進行了數值模擬，研究發現：振動圓柱受到的流體力要遠大于繞流的情況，多圓柱振動系統之間的相互作用使得其振動響應也遠大于孤立圓柱工況。

對于多圓柱耦合振動情況，Zhao等[19-20]對低雷諾數下串列與并列的剛性耦合雙圓柱渦激振動研究發現，剛性耦合與獨立工況下的圓柱振動響應存在明顯差異。當L*較小時，剛性耦合的并列雙圓柱結構中出現了馳振現象。Han等[21]對L*= 4.0、Re= 103～3×104和不同入射角度(α= 0°～60°)情況下的正三角形排列剛性耦合圓柱渦激振動進行了研究，結果表明，入射角對鎖定區間有較大影響，最寬與最窄的鎖定區間分別出現在入射角α=15°與α=0°處。在α=60°和Ur>12.0時出現了馳振現象。Han等[22]進一步對正三角形排列耦合圓柱在L*= 1.5、Re=3×103～1.6×104、Ur=3～16和入射角α= 0°～60°工況下的渦激振動進行了數值模擬研究，發現最寬與最窄的鎖定范圍分別出現在α=60°與α=0°情況下。

綜上，目前對三角形排列剛性耦合圓柱渦激振動的研究還比較有限，部分研究考慮了來流攻角對振動響應的影響，而忽略了間距比的影響。基于此，本文研究均勻來流下間距比對正三角形排列剛性耦合圓柱渦激振動的影響，詳細分析圓柱振幅、響應頻率、水動力系數、相位差以及尾流模式等隨間距比和折合流速的變化。

1 數值方法

1.1 控制方程

流固耦合的數值模擬采用浸入邊界法[23]，其控制方程如下：

(1)

?·u=0

(2)

式中：u為速度，t為時間，p為壓強，v為運動黏滯系數，?為梯度算子，f為附加體積力矢量，代表流固耦合邊界條件。

采用二階精度的Adams-Bashforth時間格式對以上控制方程進行離散，可得控制方程的守恒形式為

(3)

?·un+1=0

(4)

式中：h=?·(-uu+v(?u+?uT)由對流項與擴散項組成，上標T為矩陣轉置，附加體積力表示為：

(5)

式中：I和D為插值函數，Vn+1為物面邊界的速度，上標n+1，n+1/2，n，n-1為時間步。

針對傳統浸入邊界法施加邊界條件精度不高的情況，Ji等[23]提出了基于嵌入式迭代的浸入邊界法，將浸入邊界法嵌入到壓強泊松方程的迭代求解中，利用壓強的中間解比初始值更接近真實值的特點，迭代修正附加體積力，在不顯著增加計算耗時的前提下，提高了整個算法的求解精度。有關浸入邊界法的細節，請參考文獻[23-24]，此處不再贅述。

對僅做橫流向運動的剛性圓柱，其運動方程可以用下述方程來描述：

(6)

式中：M為圓柱質量，Y表示位移，C為結構阻尼，KY為彈簧剛度系數，FL為圓柱受到的橫流向流體力。方程采用標準的Newmak-β法求解。

1.2 問題描述

如圖1所示，編號為1、2和3的三等直徑圓柱按等邊三角形布置于計算域中心。其中，間距比L*分別為1.0、1.6、2.5和4.0。圓柱間剛性連接，形成單自由度振動系統[25]。圓柱質量比為m*=M/Mf= 2.0，阻尼系數設為C= 0。雷諾數為Re=UD/ν= 100和折合流速為Ur=U/fnD= 3.0 - 30.0。以上參數中，M為三個圓柱的質量，Mf為等體積流體質量，U為來流流速，取為1.0，ν為運動黏性系數，fn為圓柱固有頻率，D為圓柱直徑，取為1.0。采用正交笛卡爾網格對計算域進行劃分，笛卡爾坐標系位于等邊三角形中心。計算域大小取為200D×200D，有效地避免了邊界對流場的影響[26]。三個圓柱連線的中心到入口、出口以及上、下邊界的距離均為100D，如圖1所示。為保證計算精度，對圓柱周圍的網格進行加密，其中加密區域大小為8D×8D，對應的網格尺度為Δx/D=Δy/D= 1/64，該網格精度可以較好模擬多圓柱的渦激振動問題[27]。圖2給出了圓柱體周圍網格的放大圖。為節省計算資源，加密區域外的網格間距以等比形式增加。本文采用768(流向)×768(橫向)的正交網格，總結點數約為59萬。

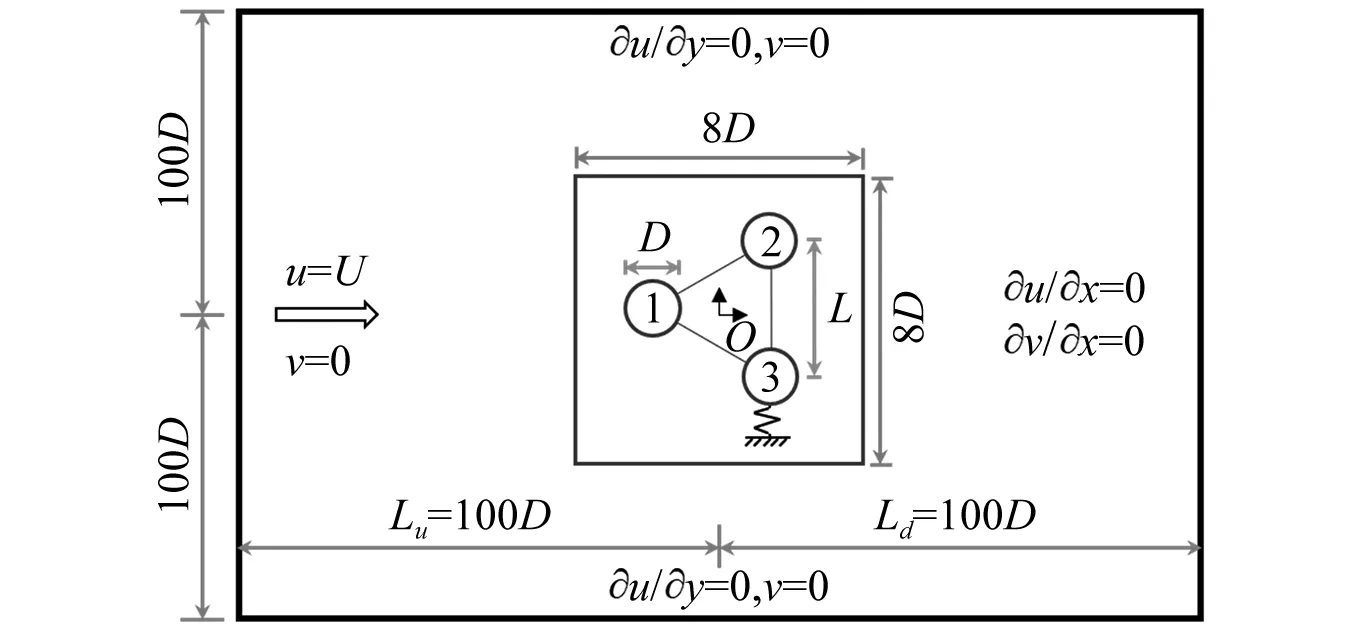
圖1 三角形排列三圓柱渦激振動的計算域和邊界條件

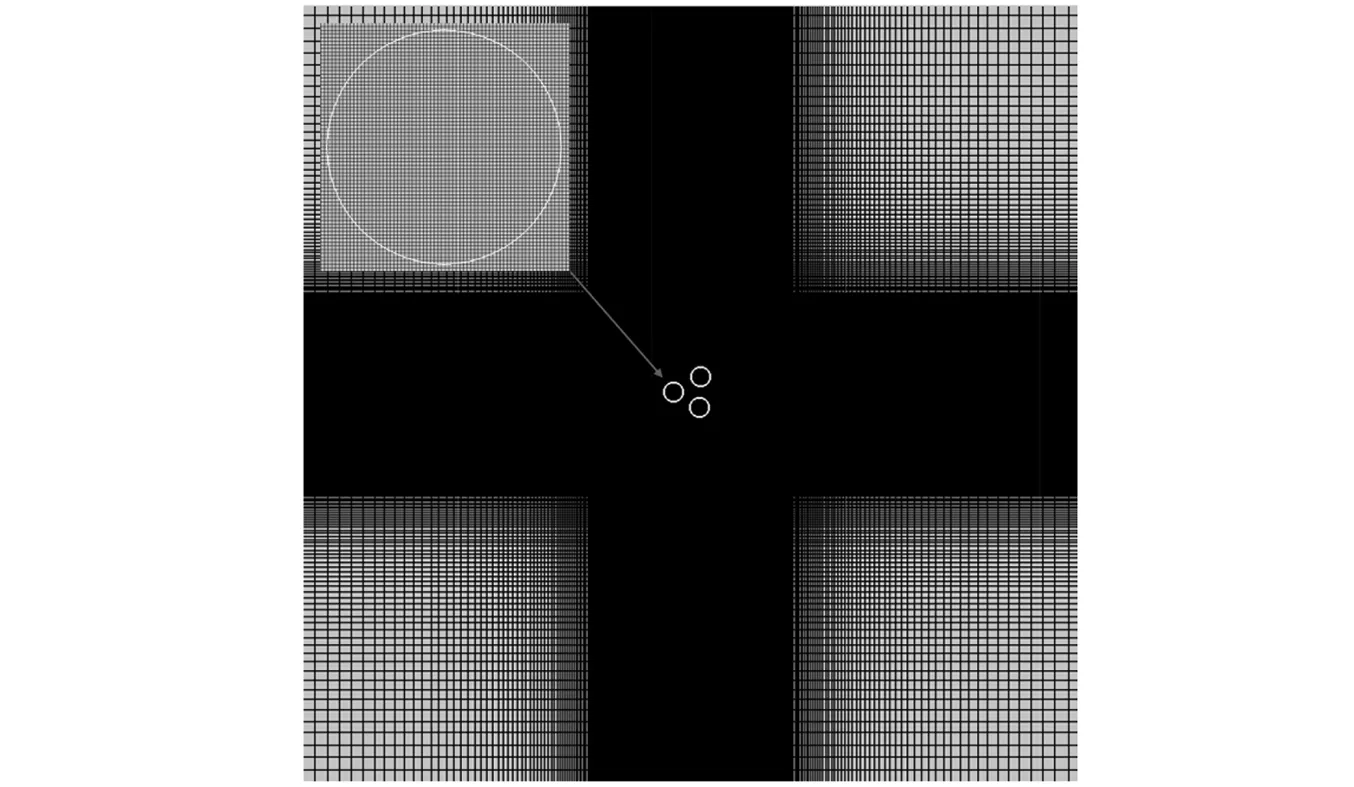
圖2 網格劃分和局部放大圖

邊界條件設置如下：入口為Dirichlet型邊界(u=U,ν=0)，出口為Neumann型邊界(?u/?x=0，?v/?x=0)，上下為可滑移邊界(?u/?y=0，ν=0)。

2 程序驗證

為驗證本文數值方法的精度，針對剛性耦合并列雙圓柱的渦激振動問題進行有效性驗證。采用與Zhao等[19]相同的參數，并將結果與Zhao等[19]進行比較。具體參數為雷諾數為Re= 150，質量比為m*= 2，阻尼比為ζ=0。采用與Zhao等相同的計算域：50D×80D，其中Lu= 20D和Ld= 30D。算例中，兩圓柱的中心間距為4D，振幅的定義與Zhao等相同，為A=(Ymax-Ymin)/2D。由圖3可知，本文的模擬結果與Zhao等吻合良好，從而驗證了本文數值方法和程序的正確性。

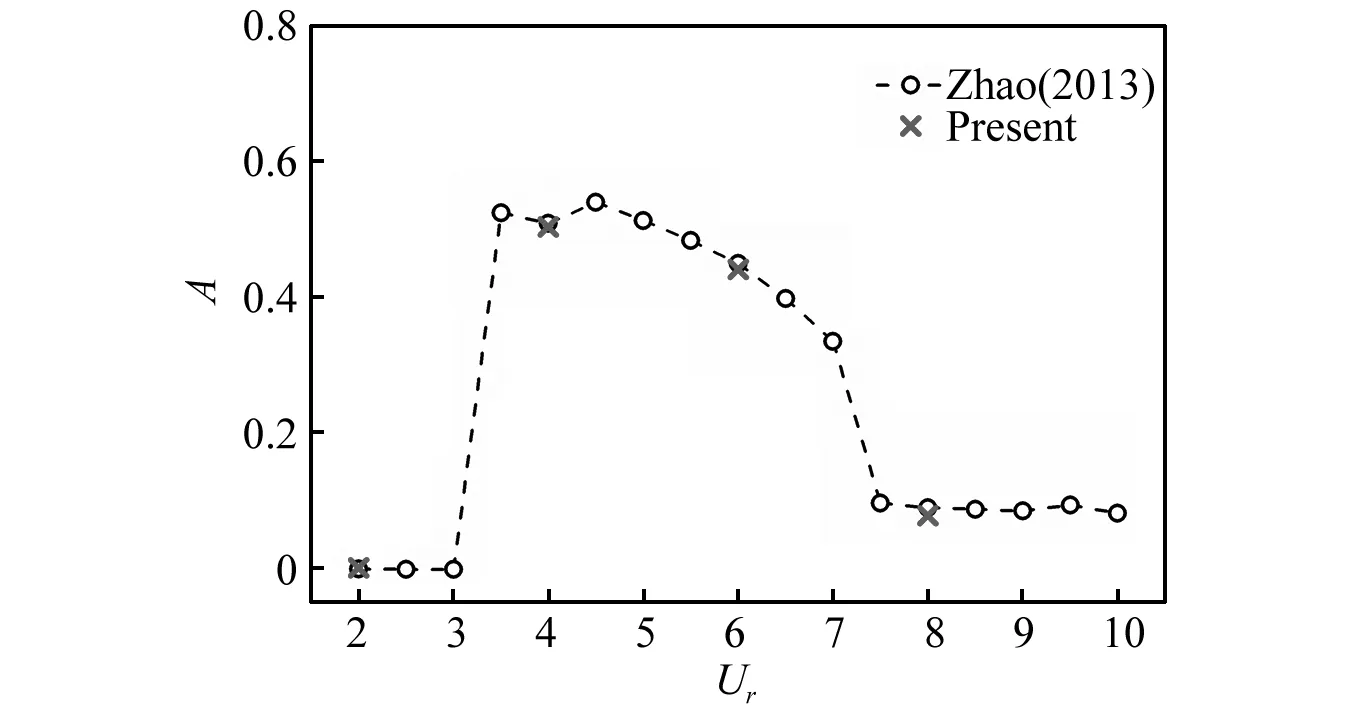
圖3 剛性耦合并列雙圓柱振幅隨折合流速的變化情況

為保證數值收斂，模擬需滿足CFL(courant-friedrichs-lewy)條件，即ΔtU/Δx≤0.5。分別選定無量綱時間步長ΔtU/D為0.002與0.004，考察時間步長對正三角形排列剛性耦合三圓柱渦激振動在L*= 1.0和Ur=9.0條件下的特征參數的影響。如表1所示，兩組結果的最大誤差僅為1.9%。因此，采用ΔtU/D=0.004時，模擬結果是收斂的。此外，本文所采用網格(Δx/D=Δy/D=1/64)的收斂性在已發表文獻[27]中進行了充分驗證，出于簡潔的目的，本文并未給出。

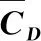
表1 正三角形排列剛性耦合三圓柱渦激振動對比，其中表示阻力均值，為阻力脈動值，為升力脈動值，Ay/D為橫向無量綱振幅， St為圓柱的脫渦頻率，括號內為兩者的誤差百分比

3 結果和討論

3.1 振動響應

圖4 不同間距比下圓柱振幅(A*)、頻率比(fosc/fn)與St數隨折合流速變化情況

L*=1.6與2.5振動響應同樣分為四個分支，且對應的Ur范圍相同，即3.0≤Ur<4.0(DS1)、4.0≤Ur<5.0(IB)、5.0≤Ur<10.0(LB)和10.0≤Ur≤30.0(DS2)。此外，兩者LB的振幅均存在較大的波動。所不同的是，L*=1.6時，最大振幅在LB的末端取得，而L*=2.5時，最大振幅在LB的前端取得。此外，在DS2內，前者的振幅單調緩慢遞減，而后者的振幅存在緩慢增大的趨勢。在振動頻率方面，兩者也存在異同。例如，兩者均存在鎖定區間，且鎖定區間的范圍相同；鎖定區間內，頻率的變化較緩，且接近固有頻率；在DS1和IB之間，振動頻率存在一個小幅跳躍。然而，在DS2內，兩者存在明顯區別。L*=1.6時，振動為單頻振動，振動頻率遵從St隨折合流速線性變化；L*=2.5時，振動存在兩個相當的卓越頻率，分別稱為渦振頻率和馳振頻率，其中渦振振動頻率遵從St變化，而馳振頻率變化不大，且小于固有頻率(馳振的特性)。此方面的詳細分析可見3.3節。

L*=4.0時，圓柱的振動響應可以分為IB、LB和DS2分支，分別對應3.0≤Ur<6.0、6.0≤Ur<11.0和11.0 ≤Ur≤30.0。隨著折合流速的增大，振動振幅先快速增大，后逐漸減小。振動頻率遵從St變化，隨折合流速線性增加，未出現鎖定區域，因此本文稱之為非鎖定渦激振動。圓柱的振幅在共振點處(Ur= 6.0，fosc/fn=1.0)達到最大值。

對比四種不同的間距比，可見L*=1.0的振幅明顯高于其他工況，這與圓柱間不存在間隙流動，三個圓柱構成一個單一鈍體有關。對于另外的三個工況，隨著間距比的增大，圓柱的最大振幅逐漸增大，且DS2的振幅也較大。

3.2 流體力

圖5 不同間距比下流體力隨折合流速變化情況

為了進一步對比每一個圓柱的受力變化，圖6～8分別給出了不同間距比下三個圓柱的阻力均值、升力均方根和升力均值隨折合流速的變化情況。可以看出，當L*=1.0時，上游圓柱的阻力均值隨折合流速的增大先減后增，這與下游圓柱阻力均值的變化趨勢相反。然而，對于另外三個工況，上、下游圓柱阻力均值的變化趨勢相同，均為先增后減。需要注意的是，當L*=1.6時，兩個下游圓柱在DS1和DS2分支上的阻力均值不相等，這與偏斜的間隙流動以及所形成的寬-窄尾流有關(見圖13(e)和(h))。類似的情況也出現在并列雙圓柱渦激振動中[24，29]。

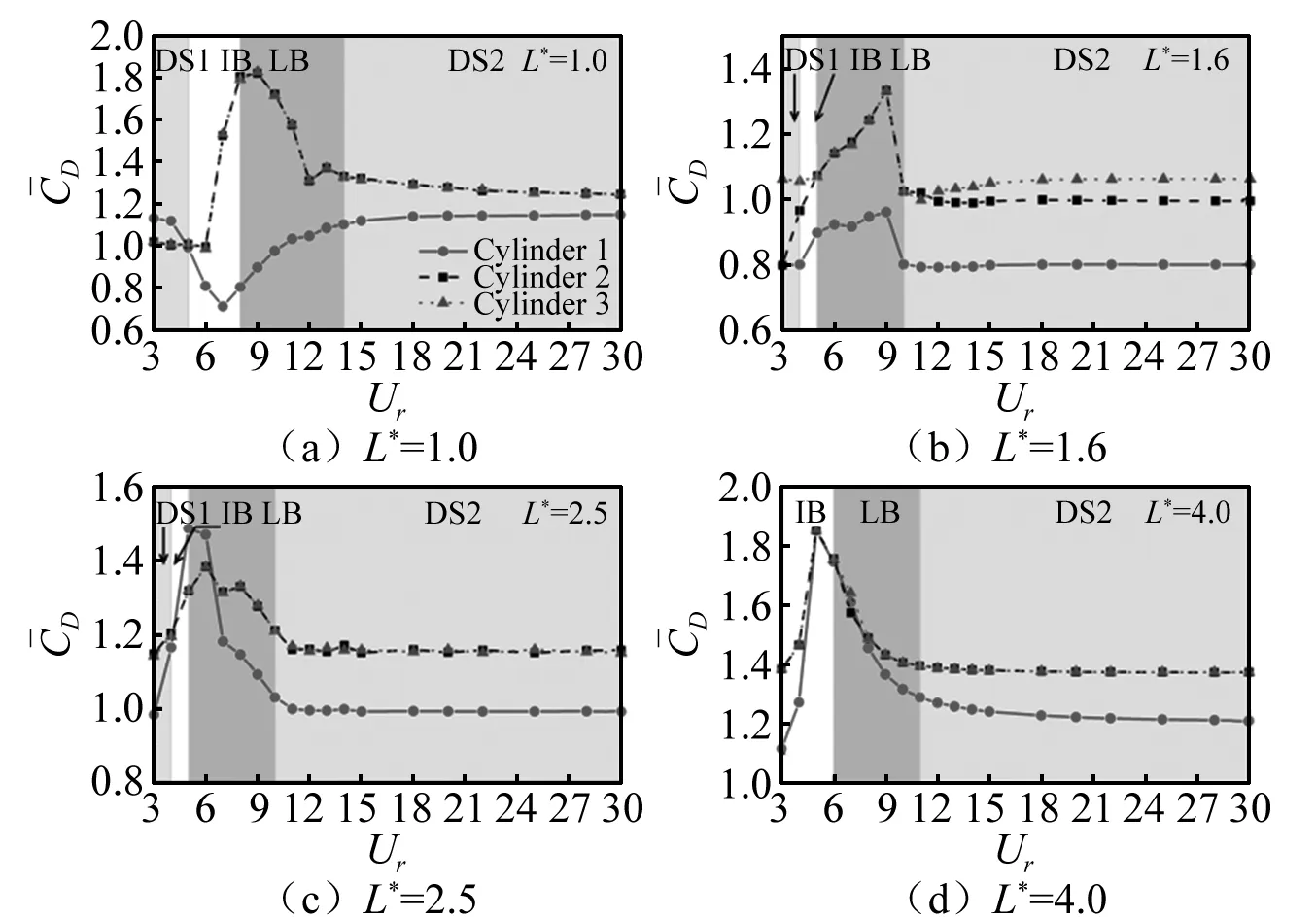
圖6 不同間距比下三圓柱阻力均值隨折合流速變化情況

如圖7所示，上、下游圓柱的升力均方根值均隨著折合流速的增大而先增后減。整體上看，隨著間距比的增大，上游圓柱的升力均方根值逐漸小于下游圓柱的。當L*=1.6時，在DS2分支上，三個圓柱的升力均方根值均接近于零，說明三個圓柱的剪切層在近尾流區均沒有發生旋渦泄放。結合此情況下下游圓柱不等的阻力均值，可知：下游圓柱在近尾流區形成四條相對穩定的剪切層，其中外部的剪切層只發生小幅擺動，沒有旋渦脫落，而內部的剪切層穩定地偏斜向一側，如圖13(h)所示。

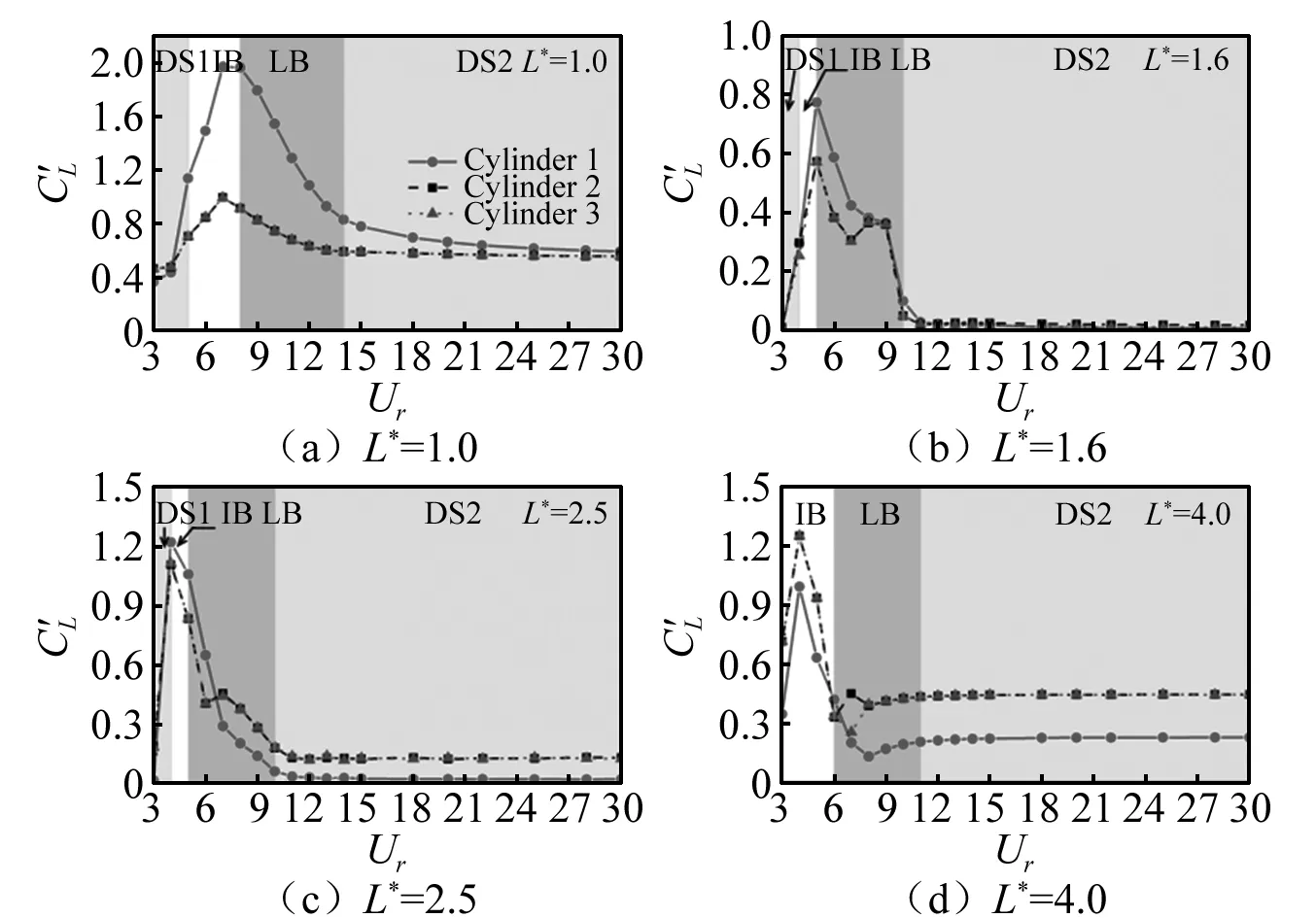
圖7 不同間距比下三圓柱升力均方根隨折合流速變化情況

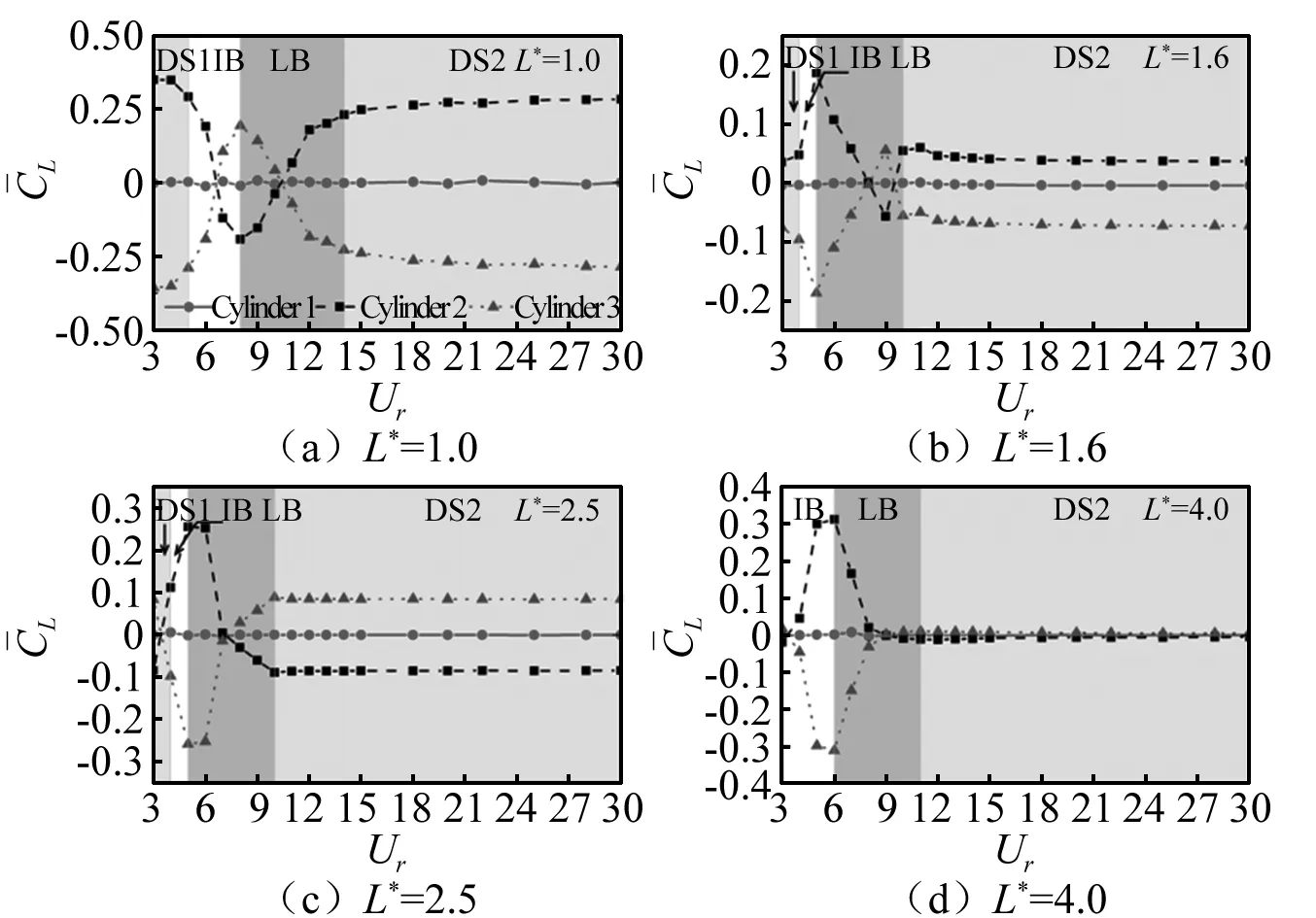
圖8 不同間距比下三圓柱升力均值隨折合流速變化情況

3.3 歷時曲線與頻率響應

圖9為不同間距比下圓柱的總升力系數與位移歷時曲線。如圖9(a)～(c)所示，當L*= 1.0時，除了Ur=5.0時升力和位移歷時曲線出現拍現象以外，其他兩個折合流速下升力和位移均表現為規則的正弦變化。這與升力和位移在Ur=5.0有兩個相當的卓越頻率，而在其他折合流速上僅有一個主頻的情況一致(如圖10(a)所示)。當L*=1.6時，DS1與IB分支的升力和位移均表現為正弦變化(如圖9(d)所示)，而在LB和部分DS2分支上，升力和位移表現為明顯的拍振(如圖9(e)～(f)所示)，此時圓柱振動由多個頻率成分組成(如圖10(b)所示)。當Ur>15.0時，升力和位移又恢復到規律的正弦變化。對于L*=2.5的情況，當Ur=3.0時，升力和位移出現拍振，如圖9(g)所示。在IB和LB分支，升力和位移轉變為穩定的周期變化，如圖9(h)所示。而在DS2分支上，升力和位移呈現不規則波動，這與升力和位移的多頻特性有關(見圖10(c))。

圖9 不同間距比下圓柱總升力系數與位移時程曲線

圖10 不同間距比下圓柱升力系數與位移的頻譜圖

當L*=4.0時，升力和位移在大部分折合流速下均呈現為規律的正弦變化，僅在Ur= 7.0時升力出現了非正弦的周期變化(如圖9(k)所示)，這與升力出現顯著的二階和三階倍頻分量相對應，如圖10(d)所示。倍頻的出現與升力與位移相位差的跳躍有關[30-31]。綜合以上分析可知，圓柱的升力和位移在大多數折合流速下為單頻主導，相應地，歷時曲線表現為規律的正弦變化。不規律的歷時曲線主要出現在L*=1.6和2.5工況下的DS2分支上，對應折合流速范圍分別為Ur=9.0～15.0和Ur=11.0～30.0，這與中等間距比下圓柱之間強烈的相互作用有關。

圖11給出了不同間距比下不同圓柱升力以及總升力頻率的變化情況，其中，fL0，fL1，fL2與fL3分別為總升力頻率和圓柱1、2、3升力頻率。當L*=1.0時，圓柱之間的間隙為零，柱間流動不存在，因此，三個圓柱的升力頻率與總升力頻率相等。當L*=1.6時，圓柱系統振幅在Ur=8.0～9.0時達到最大，下游兩圓柱的內側剪切層脫落旋渦(見圖13(g))，使得下游兩圓柱的升力頻率兩倍于上游圓柱以及總圓柱的升力頻率。在其余折合流速下，振幅相對較小，下游兩圓柱的內側剪切層不脫落旋渦，上下游圓柱的升力頻率與總升力頻率相等。當L*=2.5時，柱間流動和尾渦模式在不同折合流速上呈現顯著變化，導致升力頻率變化復雜。如圖11(c)所示，上游圓柱的升力頻率與總升力的第一主頻幾乎完全相等，而下游兩圓柱的升力頻率則明顯不同，總體上略大于上游圓柱的升力頻率和總升力的第一主頻。當L*=4.0時，較大的間距使得旋渦可以從各圓柱上自由脫落。當振幅較大時，從上游圓柱脫落的旋渦直接“撞擊”在下游圓柱上，使得下游兩圓柱升力頻譜中出現了主導的兩倍頻成分 (圖11(d))。

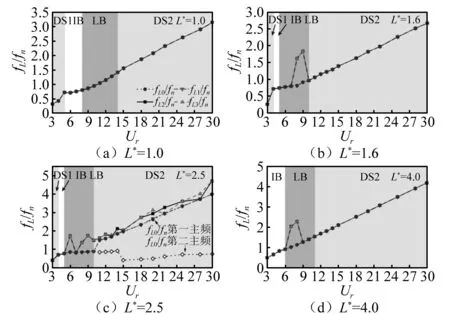
圖11 不同間距比下不同圓柱升力與總升力頻率的變化

圓柱升力和位移相位差反應了旋渦脫落時機的變化。應用希爾伯特變換求得升力和位移的相位差，并使其在[-90, 270]范圍內，相位差均值通過時間平均得到。圖12給出了不同間距比下圓柱升力和位移之間相位差隨折合流速的變化情況，其中，φ0，φ1，φ2與φ3分別表示三圓柱總升力、圓柱1，2，3升力與位移之間的相位差。根據圓柱升力與位移的相位差可判斷圓柱在振動系統中起到的作用。可以發現，總升力與位移相位差均出現了相位跳躍現象。當L*=1.0、1.6和4.0時，相位跳躍的幅值為180°。而L*=2.5時，相位跳躍的幅值約為150°，而后相位差隨著折合流速遞減至125°左右，這與該間距比下DS2分支的多頻特性有關。此外，雖然不同間距比下總升力-位移相位跳躍對應的折合流速并不完全相同，但均出現在LB分支內部或者兩端。對比圖12和圖4可以發現，相位跳躍發生的折合流速恰好對應fosc/fn=1.0。這是由于升力位移相位跳躍是線性振動系統的固有特性，當振動頻率跨過固有頻率時，就會出現相位跳躍。

圖12 不同間距比下升力和位移相位差隨折合流速的變化

進一步還可發現，當L*=1.0時，下游兩圓柱相位差處于0°～150°之間，隨著折合流速的增大而逐漸增大。而上游圓柱的相位差一直位于小于零(Ur≤18.0)或者大于180°(Ur>18.0)的區間內。Ji等[32]指出：升力位移之間的相位差決定了能量在圓柱振動和流動之間的傳遞方向。當相位差在0°～180°之間時，圓柱升力做正功，能量由流動傳遞給圓柱振動；反之，當相位差在180°～360°之間時，圓柱升力做負功，能量由圓柱振動傳遞給流動。由此可見，下游圓柱對整個系統的振動起促進作用，而上游圓柱對整個系統的振動起抑制作用。

如圖12(b)所示，當L*=1.6時，圓柱1升力做負功(Ur=3.0除外)，抑制振動。當Ur≤10.0時，圓柱2和3做正功，促進振動；當Ur≥12.0時，兩圓柱的相位角不等，圓柱3做正功，促進振動，而圓柱2做功幾乎為零(相位角等于0°或者180°時，升力做功為零)。這主要與下游兩圓柱的偏斜間隙流有關(如圖13(h)所示)。高折合流速時，窄尾流圓柱(圓柱3)的升力較大，對振動起促進作用，寬尾流圓柱(圓柱2)的升力較小，對振動幾乎不起作用。

當L*=2.5時，由于多頻存在，升力主頻與位移的相位差呈現明顯雜亂變化。總體上看，上游圓柱在大折合流速做正功，在小折合流速做負功，而下游兩圓柱則幾乎在所有的折合流速上做正功。需要指出的是：由于升力的多頻特性，相位差隨時間波動較大，相位差的均值并不能完全代表圓柱做功情況。當L*=4.0時，上游圓柱在Ur≤7.0時起抑制作用，在Ur>7.0以后起促進作用，而下游兩圓柱的情況則正好相反。

可見，不同圓柱對系統振動的貢獻是有區別的，且隨間距比變化。間距比小時，上游圓柱做負功，抑制振動，下游兩圓柱做正功，促進振動。而當間距比較大時，上游圓柱在折合流速較小時做負功，抑制振動，而在折合流速較大時做正功，促進振動。下游兩圓柱的做功情況與上游圓柱相反。

3.4 尾渦結構

為了更好地理解柱群渦激振動現象，圖13給出了各間距比下不同分支內的尾渦結構。

當L*=1.0時，三圓柱彼此相貼，圓柱間不存在間隙流動，上游圓柱的剪切層完全包裹下游圓柱，并從下游圓柱的兩側交替脫落，形成2S尾流模式，與單鈍體的情況類似。隨著振幅的變化，圓柱后的尾渦結構呈現不同的特性。當振幅較小時(DS1分支)，尾渦表現為交錯渦街，如圖13(a)所示。當振幅較大時，兩渦列之間的橫向距離逐漸增加，在圓柱后形成平行渦街，如圖13(c)～(d)所示。

對于L*=1.6的工況，當Ur=3.0和13.0時(DS分支)，圓柱的振幅幾乎為零，上游圓柱的剪切層“堆積”在圓柱間，一小部分與下游圓柱外側的剪切層融合，如圖13(e)和(h)所示。此外，下游圓柱間的間隙流動偏向于圓柱3，形成了寬-窄尾流。結合圖6(b)、8(b)可知，寬尾流圓柱所受的平均阻力較小，平均升力(斥力)較小；而窄尾流圓柱則與之相反。由于間隙剪切層較長且無明顯擺動，下游圓柱外側的剪切層卷起形成旋渦的位置距離下游圓柱較遠，因此下游圓柱受到的升力很小，如圖5(b)和7(b)所示。當圓柱振幅較大時(LB分支)，如Ur=5.0和9.0，隨著圓柱的上下振動，上游圓柱的剪切層交替包裹其中的一個下游圓柱，在尾流中形成平行渦街和交替渦街，如圖13(f)和13(g)所示。其中平行渦街在下游發生同側旋渦融合，形成更大尺度的二次渦街，二次渦街頻率會顯著低于平行渦街的情況[33-34]。

圖13 不同間距比下尾流隨折合流速的變化情況

當L*=2.5時，由于圓柱間隙的進一步增大，當圓柱振幅較小時(Ur=3.0和14.0)，上游圓柱的剪切層完全進入下游兩圓柱的間隙(圖13(i)和13(l))，但由于受到下游圓柱的擠壓，在下游不遠處即完全耗散。下游圓柱的剪切層發生周期性的旋渦泄放，但內部剪切層脫落的旋渦發生融合，很快消散。當圓柱的振幅較大時，上游圓柱的剪切層交替包裹下游圓柱，剪切層與下游柱體發生強烈的相互作用，尾流變得很不規律。當Ur= 5.0時，三圓柱同相瀉渦，在圓柱下游形成了四列彼此平行的渦街，由于振幅達到最大值，上游圓柱的剪切層在柱間發生泄渦，并“碰撞”下游圓柱表面，如圖13(j)所示。

當L*=4.0時，柱間間隙已經大到上游圓柱的剪切層可以在柱間卷起并脫落旋渦。當振幅較小時，上游圓柱的泄渦從下游圓柱間通過，并與下游圓柱的泄渦發生配對、融合，在下游形成較為規則聯合渦街，如圖13(m)和(p)所示。在IB分支，當Ur= 5.0時，振幅接近最大值，上游圓柱脫落的旋渦直接撞擊到下游圓柱上，并從下游兩圓柱的兩側分離，在下游形成穩定的四列渦街，如圖13(n)所示。Ur=7.0的工況與Ur= 5.0類似，但下游圓柱后方形成寬-窄尾流模式，對應不相等的阻力均值和升力均值和均方根值，如圖6(d)、7(d)和8(d)所示。DS2上，圓柱的振幅顯著降低， 尾流模式又恢復到了初始分支DS1的情況。如圖 13(p)所示，內側旋渦強度低于外側，上游圓柱的旋渦與下游圓柱內側旋渦配對，并在下游形成三列渦街。

4 結 論

對三角形排列的剛性連接三圓柱渦激振動進行了數值模擬研究，其中，雷諾數為Re=100，質量比為m*=2.0，折合流速Ur=3.0～30.0，間距比L*=1.0～4.0。基于振動振幅和頻率的特點，將圓柱的振動響應分為四個分支，詳細分析了振動振幅、流體力系數、振動頻率、歷時曲線、升力與位移相位差以及尾流模式等在各響應分支的變化情況。主要結論如下：

(1)根據振動振幅和頻率隨Ur的變化，將振動響應劃分為初始分支(IB)、下端分支(LB)與非鎖定區域(DS)，其中非鎖定區域又細分為前非鎖定區域(DS1)和后非鎖定區域(DS2)。各間距比下，隨著折合流速的增大，圓柱的振幅均呈現先增后減的趨勢，其中最大振幅(A*=1.11)出現在L*=1.0、Ur=8.0工況。隨著間距比的增大，圓柱振幅整體上表現為先減后增，L*=1.6 時圓柱的振幅明顯小于其他間距比的振幅。

(2)不同于其他間距比情況下出現的明顯的鎖定區間，L*=4.0工況下，圓柱的振動頻率隨折合流速線性變化，未出現明顯的鎖定區間。此外，當L*=2.5時，在DS2分支上，圓柱振動出現了兩個強度相當、頻率不同低頻馳振分量與高頻渦振分量。對圓柱升力主頻的進一步分析表明，在L*=1.0，1.6與4.0工況下，三圓柱升力主頻幾乎相同，下游兩圓柱僅在部分折合流速下呈現二倍頻。L*=2.5處由于復雜的柱間流動使得三圓柱升力頻率存在較大差異。

(3)DS1與IB分支上，總升力與位移同相變化，而DS2分支上，總升力與位移反相變化。總升力與位移之間的相位差在LB分支上出現了180°的跳躍。當L*=2.5時，相位跳躍約為150°，這主要是升力與位移由多頻特性造成的。不同圓柱升力與位移相位差的結果表明，間距比較小時(L*=1.0與1.6)，上游圓柱做負功，抑制振動，下游兩圓柱做正功，促進振動。間距比較大時(L*= 4.0)，上游圓柱在小折合流速時做負功，抑制振動，大折合流速做正功，促進振動；下游兩圓柱的做功情況則正相反。

(4)當間距比較小(L*=1.0與1.6)時，隨著折合流速的增大，下游圓柱經歷排斥-吸引-排斥的過程，而當間距比較大(L*= 2.5與4.0)時，下游圓柱經歷吸引-排斥-吸引的過程。由于間隙流偏斜的作用，L*=1.6時，下游兩圓柱的升阻力均值在DS2分支上不相等。

(5)當L*= 1.0時，上游圓柱的剪切層覆蓋下游圓柱，形成2S尾流模式，與單圓柱渦激振動的相似。隨間距比增加，圓柱間出現了間隙流動。L*= 1.6的DS1和DS2分支的間隙流穩定偏斜，在圓柱后方形成寬-窄尾流，造成了下游圓柱受力的不均衡。當間距比較小時，上游圓柱的剪切層不發生旋渦脫落，而當間距比較大時，上游圓柱的剪切層在柱間脫落旋渦，并與下游圓柱及其尾流發生復雜的相互作用。