普通雙體無人艇艇型綜合優化設計分析

汪保江，楊松林，程占元，施 妍

(江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003)

0 引 言

水面無人艇（USV）是無人系統中可自主完成任務的作業艇[1]，與常規載人船相比，具備體積小、速度快、靈活機動性好等特點。此外，其搭載了自主作業系統，可在無人艇上安裝雷達、水底探測聲吶和機械作業系統等系列設備，能獨立完成較為危險的任務。目前對水面無人艇的研究主要集中在各個功能模塊設計（如能源、控制、避碰、跟蹤等）、航行性能設計和無人艇協同技術[2]研究等。Ashkan Makhsoos等[3]對USV自帶的光伏系統進行了優化設計。Andrzej Stateczny等[4]研究了一種用于多任務的無人艇的通用自動控制和管理系統，對該系統進行了相關實艇的驗證性試驗。其中USV的航行性能設計分析對無人艇的綜合作業能力有著不可忽視的作用。魏成柱等[5]利用航模試驗和CFD手段等研究了一種單體穿浪滑行無人艇艇型的水動力相關特性。劉曼[6]針對一艘單體水面無人翼滑艇的性能（快速性、操縱性及耐波性）綜合優化設計分析。羅富強等[7]研究了一艘典型的高速水面無人艇在不同吃水和航行狀態下的艇體阻力性能和相關的水動力運動特性。

目前對USV的性能綜合優化設計分析主要集中在單體艇型，對于雙體艇型的優化設計分析研究較少。王超等[8]對一艘小水線面雙體無人艇進行了參數化模型設計和快速性能得優化設計。對于普通雙體無人艇的性能優化設計尚未見報道。而雙體無人艇與單體無人艇相比，具有較寬敞的甲板面積有利于布置無人艇的相關設備或者鋪設太陽能板以增強續航能力，同時相對較大的艇寬又保證了較好的穩性。且目前雙體無人艇的主要作業區域為內河湖泊，因此可以忽略波浪的影響不考慮其耐波性。綜合設計一艘性能優良的雙體無人艇是一個較為復雜的問題，其綜合性能與船型的主尺度和螺旋槳的各個參數以及電機的選型都密切相關。為了實現無人艇的綜合性能最優，可以利用多學科優化的理念進行無人艇的綜合性能設計[9]，這樣節省經濟投入并可以縮短無人艇的設計周期且為后續雙體無人艇的設計提供相關的參考。

本文選用1艘典型的不同吃水下的單體試驗艇作為性能優化設計分析的基礎，將艇型參數、螺旋槳參數和電機的轉速和功率等參數作為雙體無人艇的優化設計參數，綜合雙體無人艇的快速性和操縱性，對雙體無人艇進行綜合優化設計分析，并與常規雙體船比較。首先在艇型參數上設置較寬的片體間距以保證較大的甲板面積和更大的艇型寬度，甲板上根據不同作戰任務可布置相應的傳感器和執行器或者鋪展太陽能板以提高綜合的續航能力[10]。其次，雙體無人艇的單個片體與普通的雙體船的片體相比較為瘦長（長寬比約11∶1），可以保證更好的快速性。

1 綜合優化數學模型

1.1 設計變量

本文選擇了1艘典型不同吃水下的單體試驗艇型（長寬比約11∶1）作為優化設計的基礎艇型，其中單體試驗艇型涉及到的船型參數：船長L、 船寬B、方形系數CB、菱形系數CP、設計水線面系數CW、浮心縱向位置Lcp等都是隨著相對吃水T/Twl而變化，其中Twl為標準吃水等于0.105 4 m。

將上述參數用響應面擬合出關于T/Twl的擬合公式作為優化設計的參數，如下式：

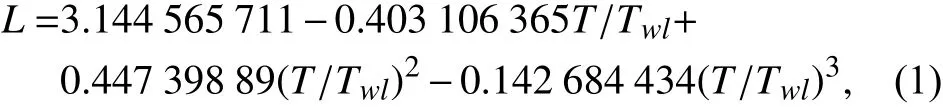
本文的設計變量選擇9個相關的參數，用一個向量X表示：

其中：吃水d，螺旋槳參數（直徑KT、盤面比KQ、螺距比VS、轉速 kn ），設計航速 ω ，重心垂向位置與型深比k/D，吃水與型深比d/D，片體內間距C。相關的變量單位：d，KT，C，m；N為r/min；VS為kn；其余為無量綱單位。

1.2 目標函數

本文高速雙體無人艇將衡量自身的快速性、操縱性作為子目標函數，以2個指數冪乘積的形式構造總目標函數：

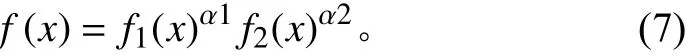
式中：f1(x)為 快速性目標函數；f2(x)為操縱性目標函數；α1為快速性權重；α2為操縱性權重需滿足α1×α2=1α1＞0,α2＞0，f1(x)，f2(x)都大于1。當f1(x)，f2(x)不滿足大于1時對其進行適當調整使其大于1。

1）快速性的子目標函數

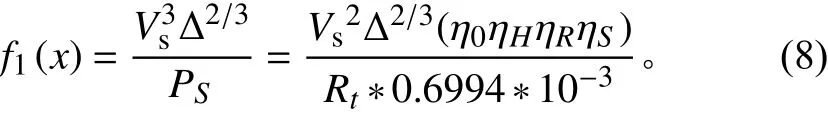
其中Rt分為Rf（摩擦阻力）和Rr（剩余阻力）。當片體中心相對距離和片體寬度之比大于2時，片體間的相互干擾較小。本文雙體無人艇的相對中心距離與片體寬度之比約為2，所以可忽略片體間的互相干擾，將整個艇體受到的總阻力看成2個孤立片體受到的總阻力。

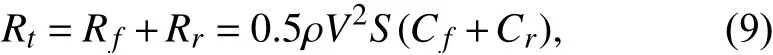
摩擦阻力系數Cf由桑海公式進行估算，當Re在106～109范圍內:

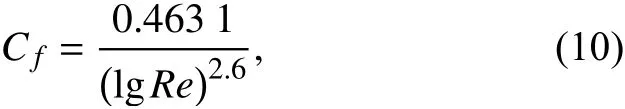
式中，Re為雷諾數：

剩余阻力系數Cr根據Cr圖譜，得到以下擬合公式：

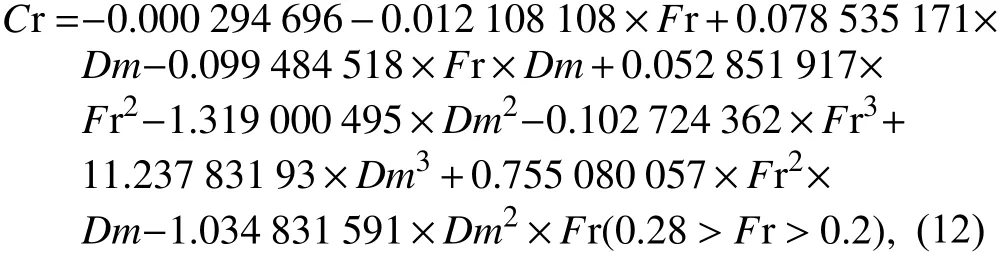
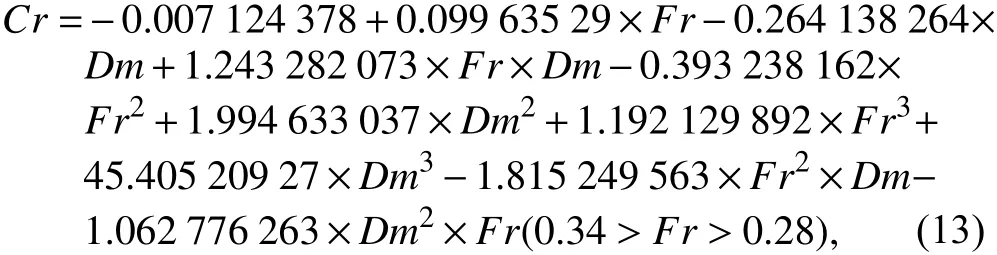
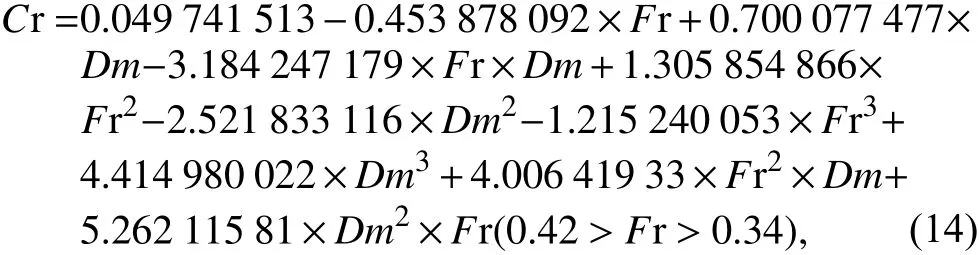
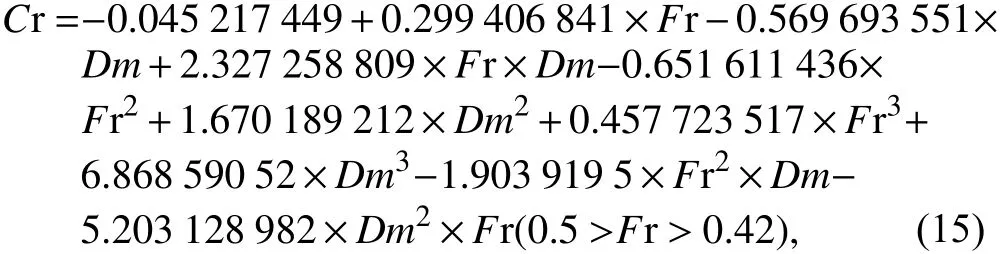
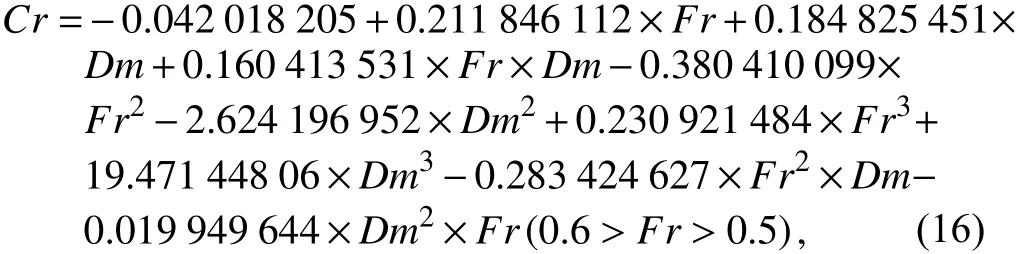
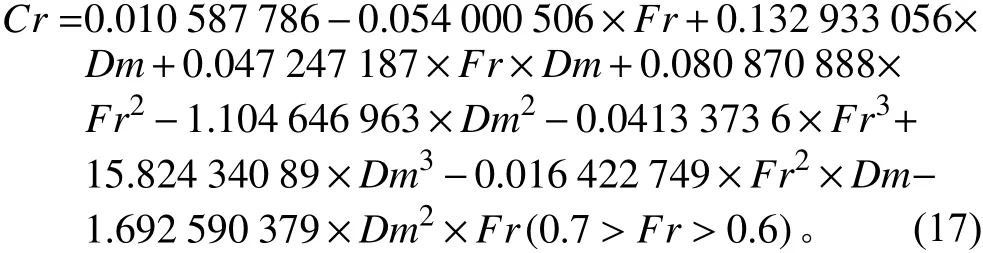
濕表面積S由試驗數據擬合得到：

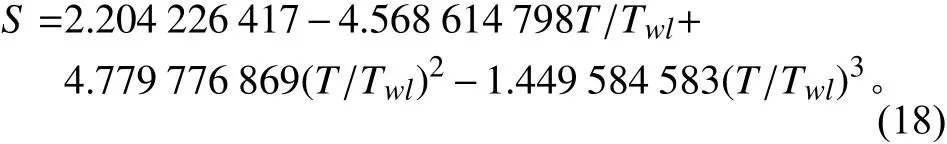
2）操縱性子目標函數

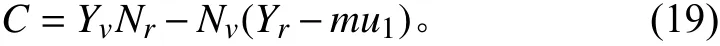
式中：C為穩定性衡準數，若C＞0時，表示船艇具有直線穩定性，C≤0，則不具有直線穩定性。當C＞0，式（19）可整理為無因次化后可得到

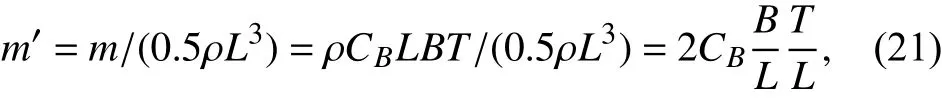
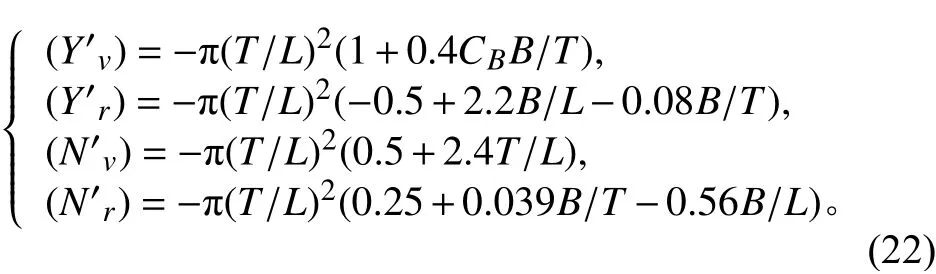
1.3 約束條件

1）等式約束

靜水浮性約束

推力和阻力平衡約束

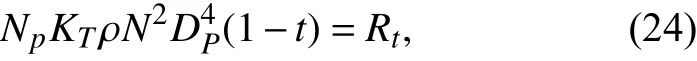
轉矩平衡約束

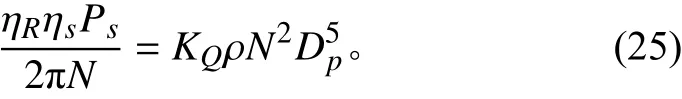
2）不等式約束

需滿足螺旋槳空泡要求，按照Keller給出的公式：

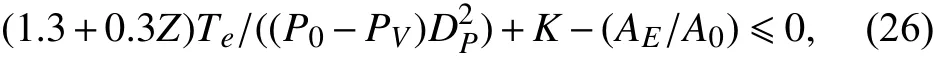
滿足穩性規范要求，即正浮初穩性高需大于0.7 m：

2 優化方法及計算策略

2.1 優化方法

本文雙體高速無人艇的綜合優化數學模型為非線性、高耦合性，在設計變量的限定范圍內可能存在著多個局部最優值。對于這類優化模型，常利用現代優化算法對其進行數值求解。

遺傳算法[12]作為一種現代優化算法，具有高效的概率搜索能力，且適用于許多數學模型較為復雜的實際應用之中。該算法利用適應度（Fitness）作為衡量染色體在進化過程中的能否取得繁衍下一代的機會或者保持自身染色體（精英保留策略[13]）直接進入到下一代之中的可能性。

種群的進化過程中，兩代之間的關系定義為父代和子代的關系，子代由父代選擇（selection）、交叉（Crossover）、變異（Mutation）而產生。標準遺傳算法計算流程如圖1所示。

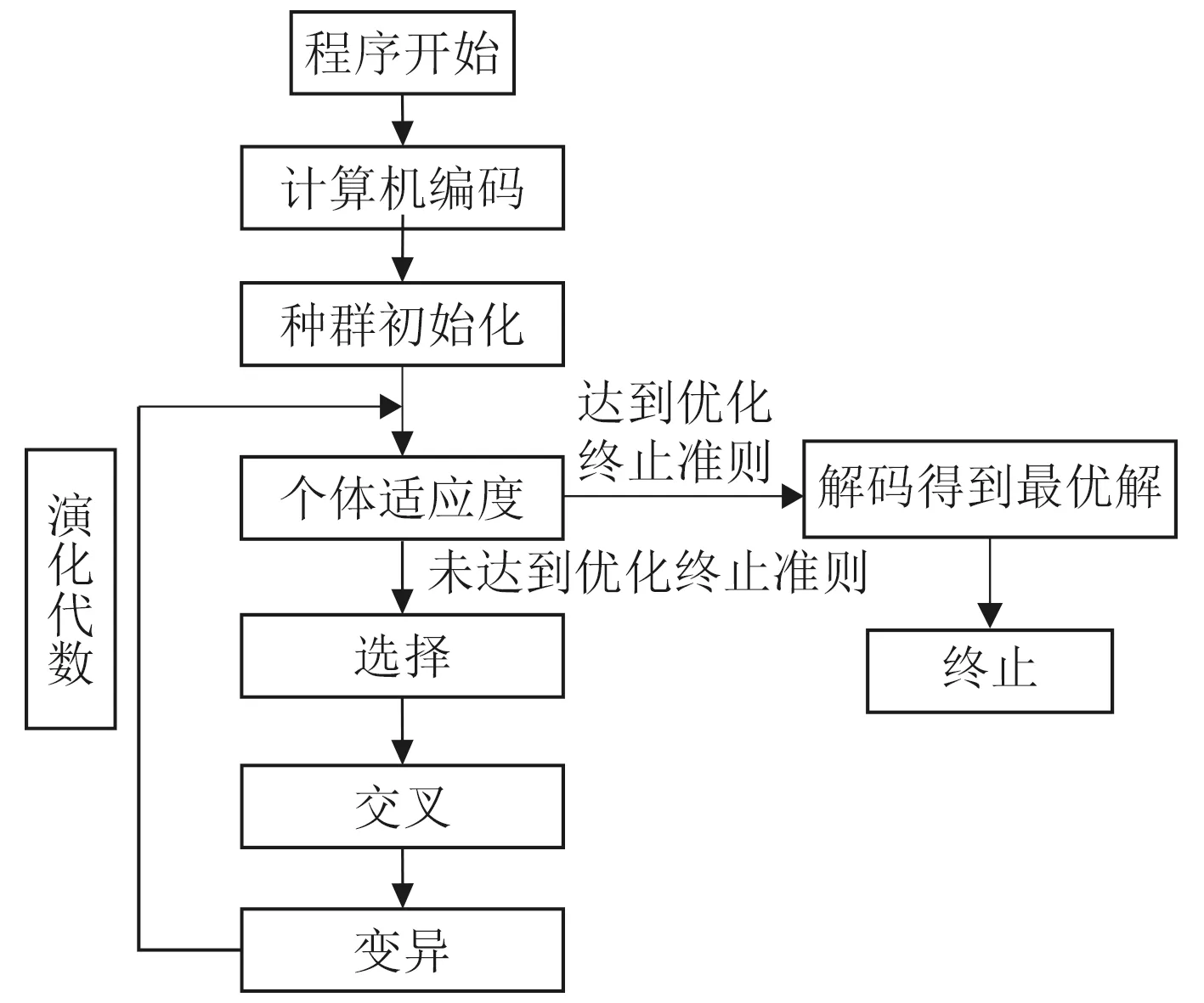
圖1 標準遺傳算法流程Fig. 1 Flow of standard genetic algorithm

標準的遺傳算法通常存在局部優化算法的早熟機制和算法對設定參數的敏感性，而且往往在后期的尋優搜索變得很低。因而有較多關于遺傳算法的改進研究，這些研究主要涉及到個體參數編碼、初始種群規模數、構造的適應度函數，遺傳算子（選擇、交叉和變異）改進、約束條件處理方式等。改進的措施主要針對以上要素進行改進和組合，目的是為了提高算法的收斂速度并且避免計算的最終結果陷入到局部最優解。

利用一種成長機制的改進遺傳算法，其優化效果優于普通的輪盤機制遺傳算法[14]，其“成長”的本質在于：將下一代產生的種群中適應度排名處于尾端的個體淘汰，被淘汰的個體數量由父代的最好的幾個個體的附近的領域隨機產生。實現該改進策略，需要確定3個參數：

sbar交班模式是依據sbar標準化溝通模式作為依據所開展的晨交班工作。其中“s”為situation,即現狀;“b”為background,即背景;“a”為assessment,即評估,“r”為recommendation,即建議[5],sbar交班模式在內分泌科晨交班中應用,就是在現狀、背景、評估、建議四個環節中不斷提供交班質量,縮短交班時間,提高醫護人員的晨交班質量。

1）載波概率，父代的鄰域范圍與整個尋優的區域。

2）進化權重，下一代被淘汰的總數量與種群規模的比值。

3）遺傳因子，選擇父代中的精英（適應度函數較大）數量與種群規模的比值。

這種改進的方式類似于“精英保留策略”和“爆炸算子”[13]。“精英保留策略”能夠防止最優解在進化過程中受到破壞。“爆炸算子”是在最優解的局部進行搜尋，根據距離最優解值的靠近程度產生不同比例的搜尋數量，簡單來說，距離最優解越近的搜尋到的數量越多。

使用成長機制的改進遺傳算法可以使得群體的進化方向朝著最優化的方向更新變化，其本質是在進行了交叉變異之后，在新的種群中再次進行篩選（從父代中找到替代子代中的較差的解）。同時載波概率上可以選擇載波概率隨著進化代數的增加而逐漸減小，如0.001～0.01，這樣的目的是為了解決最優解逐漸收斂。

采用這樣的改進算法可能造成的不足是，最后的結果只局限在最優解的領域范圍內而在一開始就被淘汰的適應度較小的個體中無法獲取足夠多的有用信息，陷入到局部最優值之中。為了解決這一改進帶來的缺點，可以適當調高變異算子的概率而提高跳出局部最優值的概率。通常變異算子的取值范圍在0.001～0.5之間[15]，可以選擇稍大的變異算子（本文選擇0.01）來提高種群規模的多樣性。

2.2 計算策略

懲罰函數的本質[16]是將存在約束的優化問題利用函數的組合方式轉換成無約束條件的優化問題，以降低問題尋優的難度。通過構造懲罰函數可以確保遺傳群體中保留部分的非可行解并可以對其染色體中存在的有利于尋找全局最優解的信息加以利用，使得遺傳的總群體構成更多樣，從而擴大尋優空間的范圍，提高搜索效率。

懲罰函數通過將建立的數學模型所有約束條件加以整合成懲罰函數P(X)，適應度函數通常采用加法和乘法2種形式組合目標函數f(X)和 懲罰函數P(X)。

加法形式的適應度函數的組合形式為F(X) =f(X) +P(X)；乘法形式的適應度函數的組合形式為F(X) =f(X) ·P(X)。

P(x) 由Pe(x) 和Pue(x) 相乘得到，即F(X)=f(X)·Pe(x)·Pue(x)。

3 計算分析

3.1 設計變量的上下限

本文設計的雙體無人艇排水量設為100 t，根據不同的航速區間，優化3種航速（低速、中速、高速）下的目標無人艇；根據單體試驗艇的標準吃水為0.105 4 m，選取試驗艇標準吃水的0.9～1.1作為吃水的設計變量上下限；根據不同吃水下擬合出的排水量確定縮尺比，從而確定最終實際無人艇的設計吃水及其他與縮尺比相關的雙體無人艇艇型參數。

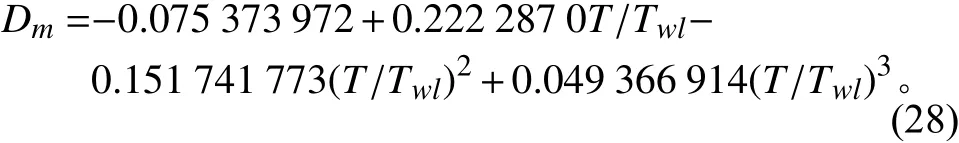
擬合排水量公式如下：其中：Dm為排水量，Twl為標準吃水；T為設計吃水。

3.2 懲罰函數參數設置

等式約束的懲罰函數構造如下：

1）浮性約束的誤差范圍設為0.001，懲罰因子設為2；

2）推力約束的誤差范圍設為0.001，懲罰因子設為10；

3）轉矩約束的誤差范圍設為0.001，懲罰因子設為10。

3.3 改進遺傳算法內部參數設置

常規參數設置（種群規模400、遺傳代數：1 000～5 000、交叉概率0.75、變異概率0.01），改進算法的特定設置（變載波概率為0.000 1～0.01、進化權重0.5、遺傳因子0.1）。

3.4 計算結果

1）設定不同子目標函數權重和不同的遺傳代數，得到的低速雙體無人艇優化結果如表1所示。

2）設定不同子目標函數權重和不同的遺傳代數，得到的中速雙體無人艇優化結果如表2所示。

3）設定不同子目標函數權重和不同的遺傳代數，得到的高速雙體無人艇優化結果如表3所示。

4 結 語

本文選擇一艘典型單體船型（長寬比約11：1），根據船型參數之間的相互關系，擬合船長、船寬等船型系列參數關于相對吃水（T/Twl）的關系式，根據剩余阻力曲線擬合了剩余阻力系數關于Fr（0.2-0.7）的相關關系。將擬合得到的參數和設定的10個獨立的船型參數作為設計變量進行雙體無人艇的優化設計分析。建立了雙體無人艇綜合性能（快速性和操縱性）優化數學模型，利用改進遺傳算法和懲罰策略參與模型計算。

依據表1～表3的優化結果，可得到如下結論：

1）優化得到的九組結果在遺傳代數為4 000～5 000代時結果開始收斂且達到最優解；

2）隨著操縱性權重的增加（0.5～2），優化結果中設計吃水也隨之增加，即不同權重下設計吃水對于優化結果最敏感；

3）快速性子目標函數在設定吃水較淺，趨近于最優解，而操縱性子目標函數則相反。具體表現為：吃水較淺時艇型更瘦長（B/L，T/L，Cb更小），快速性更好。而操縱性不僅與瘦長度相關，而且與艇體尾部的中縱剖面的投影面積大小相關（表現為T，L值越大越好）[11]。本文的優化計算結果表明，在瘦長度變化不大時（B/L，T/L和Cb變化率），即適當提高吃水的深度，有助于提高操縱性。

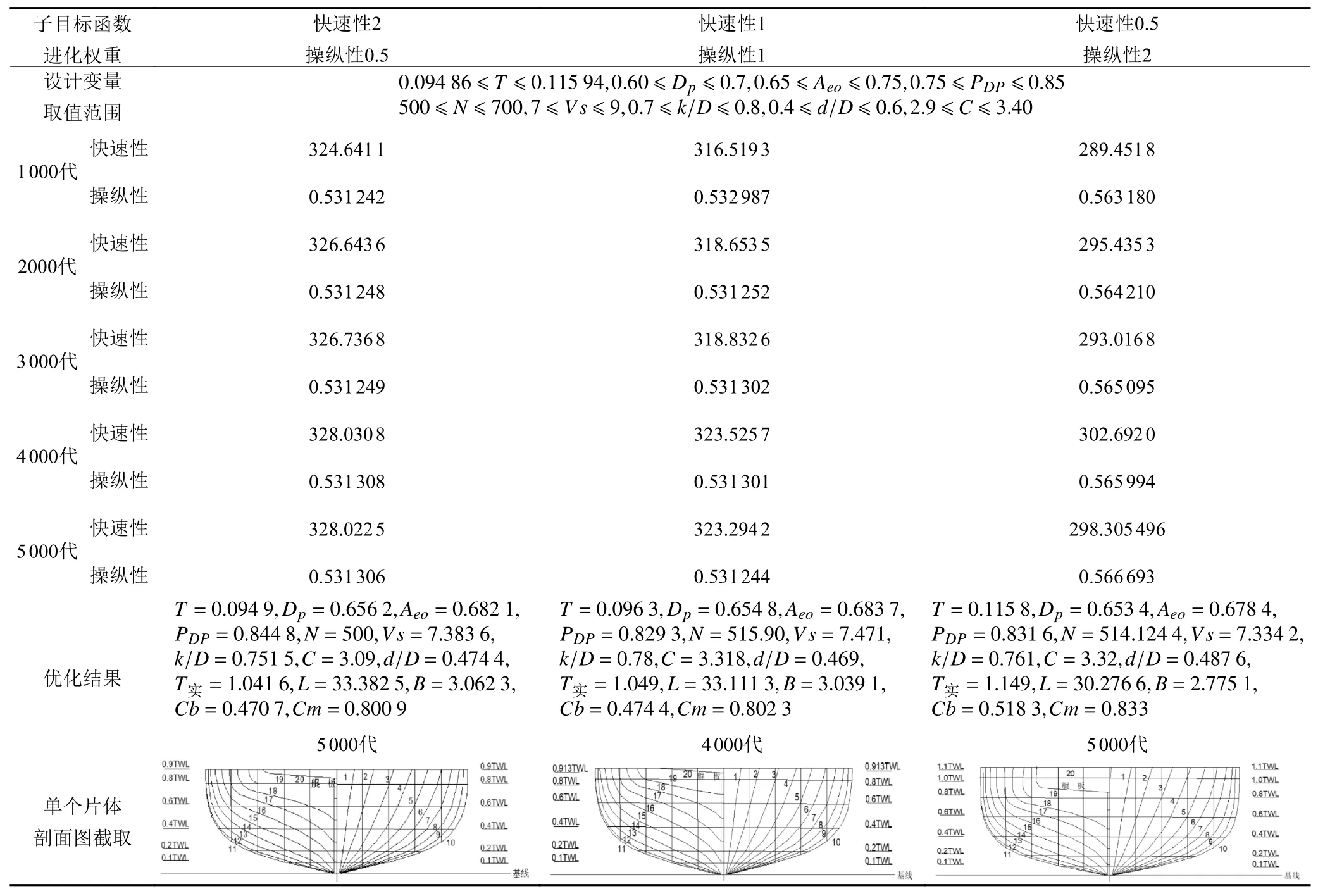
表1 不同子目標權重的優化結果隨遺傳代數的變化Tab. 1 Optimization results of different subobjective weights with genetic algebra

表2 不同子目標權重的優化結果隨遺傳代數的變化Tab. 2 Optimization results of different subobjective weights with genetic algebra

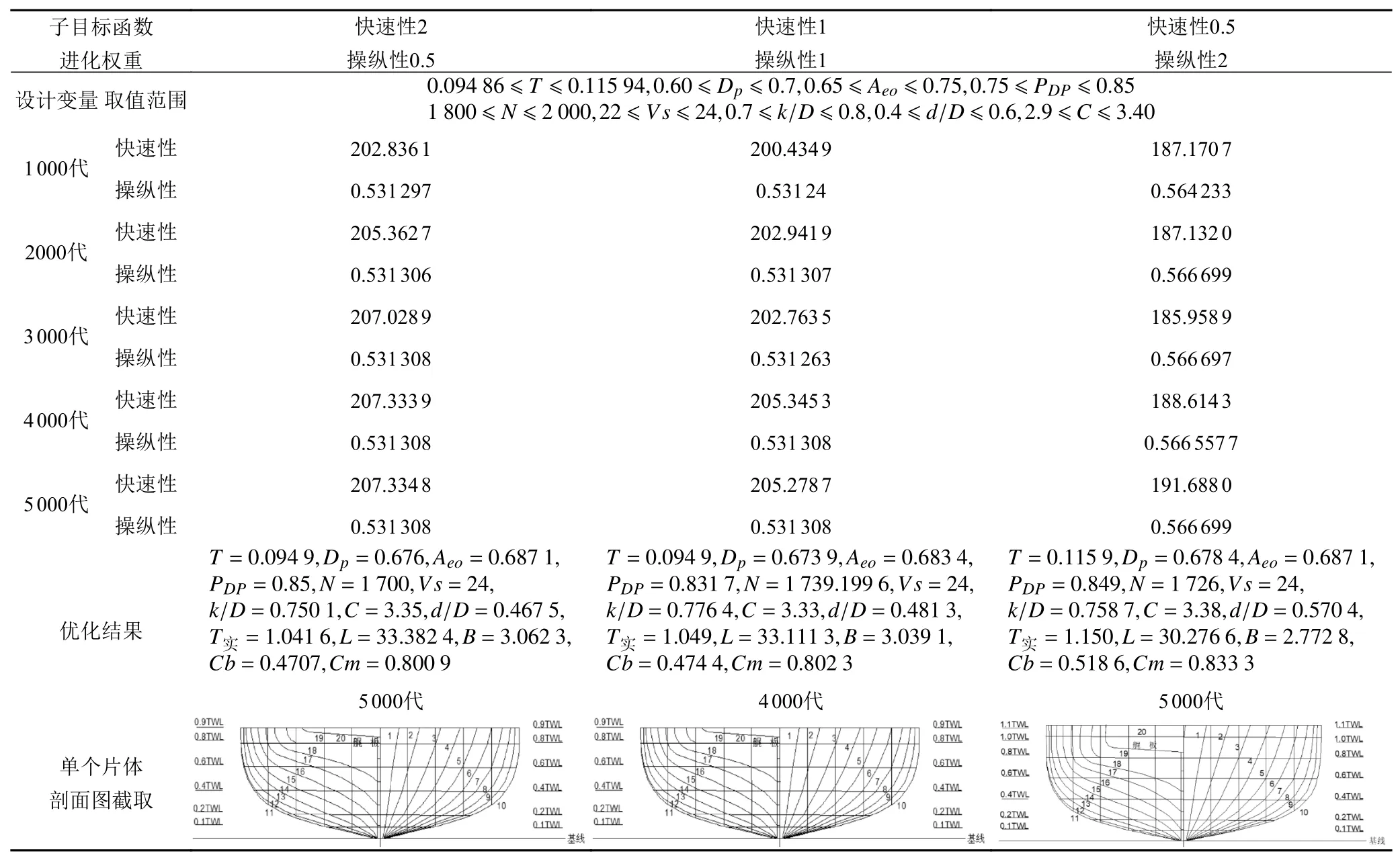
表3 不同子目標權重的優化結果隨遺傳代數的變化Tab. 3 Optimization results of different subobjective weights with genetic algebra

因為雙體無人艇的性能設計較為復雜且沒有相關的設計參考，本文利用一艘單體艇的試驗數據進行了一艘雙體無人艇的性能綜合優化分析。由于只考慮了2個性能，在今后的相關無人艇優化設計中可加入耐波性性能作為子目標函數。