基于聯(lián)合平差的船臺測量場標定方法研究

豐寅帥，彭 飛，王 中，孟慶旭

(海軍工程大學 艦船與海洋學院，湖北 武漢 430033)

0 引 言

隨著船舶制造行業(yè)的不斷發(fā)展，船舶制造所能達到的精度越來越高，對船舶制造過程中所能達到的測量精度提出了更高的要求，而傳統(tǒng)的以捶球和標尺為主的接觸式測量方法已經(jīng)逐漸難以滿足當前船舶制造行業(yè)的精度需求，因此，以全站儀為主的非接觸式高精度測量方法已經(jīng)在造船現(xiàn)場得到了廣泛應用。在目前船舶建造現(xiàn)場的測量作業(yè)中，由于船體分段尺寸較大，測量條件復雜[1]，在某一固定站位下無法完整獲取整個船體分段的尺寸和形狀數(shù)據(jù)[2]，以往常見的方法是利用全站儀進行多級轉(zhuǎn)站的形式，通過不斷的轉(zhuǎn)移測量站位來獲取船體分段多個角度的測量數(shù)據(jù)，但這種方法速度較慢，并且轉(zhuǎn)站過程本身是帶有無法消除的系統(tǒng)誤差，會造成測量精度下降等問題。因此，為了減少轉(zhuǎn)站次數(shù)，實現(xiàn)船體分段測量數(shù)據(jù)的統(tǒng)一管理，就需要在船臺區(qū)域內(nèi)構建能夠覆蓋全域的具有統(tǒng)一基準的船臺測量場[3]。

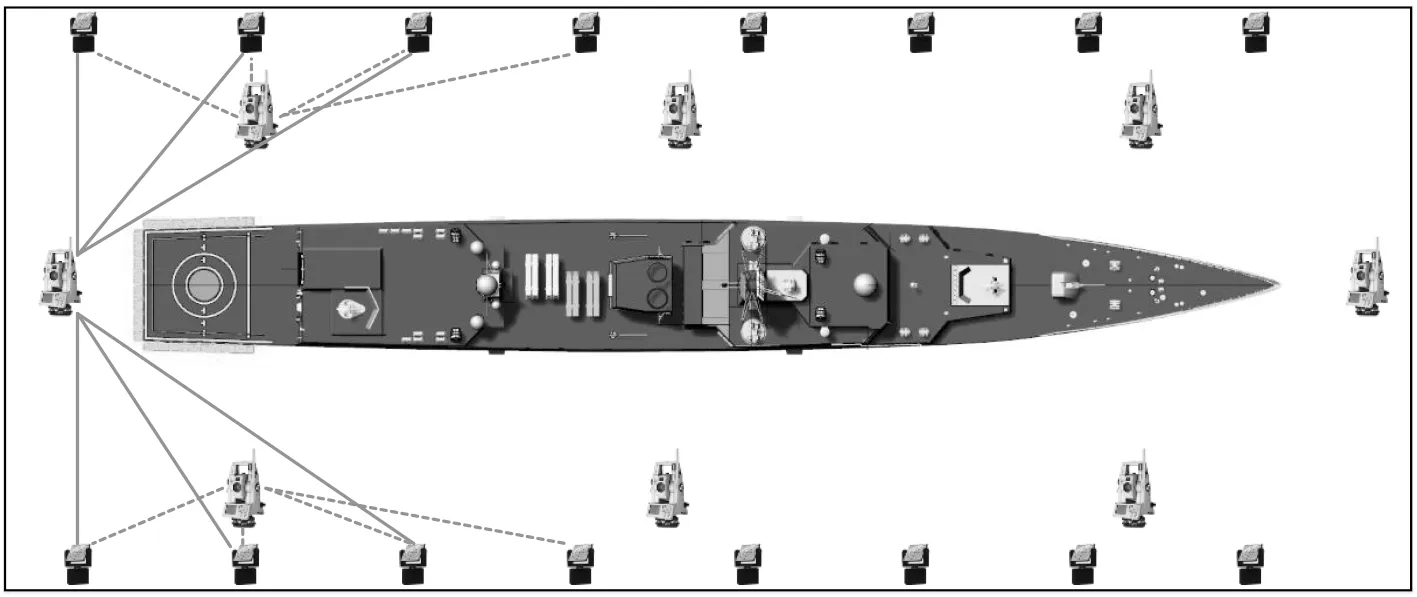
圖1 船臺測量場示意圖Fig. 1 Slipway measurement field

如圖1所示，船臺測量場是以多級轉(zhuǎn)站測量為基礎，在船臺區(qū)域內(nèi)布置相當數(shù)量的公共點，通過多次坐標轉(zhuǎn)換，將不同站位下所測得的公共點坐標統(tǒng)一到一個基準坐標系下。目前，常見的坐標轉(zhuǎn)換算法主要有奇異值分解法[4]、四元數(shù)法[5]和正交矩陣法[6]，由于坐標轉(zhuǎn)換算法本身就帶有一定的誤差，且在不同站位所測得的公共點數(shù)量可能不同，因此，在將公共點坐標轉(zhuǎn)換至基準坐標系時會引入一定的參數(shù)誤差，同時，受限于全站儀等測量設備的加工精度，在某一站位下對公共點進行測量時也會引入一定的測量誤差，進一步加大了船臺測量場的整體誤差。為了解決此類問題，就需要對船臺測量場進行標定，目前常見的方法是基于最小二乘原理[7-9]，對轉(zhuǎn)站測量得到的公共點坐標進行平差計算，從而得到滿足誤差最小時的坐標轉(zhuǎn)換參數(shù)。近年來，國內(nèi)外學者對采用平差計算方法進行了大量的研究，Schaffrin[10-12]利用拉格朗日函數(shù)構建了平差模型，并進一步推到得到了加權整體最小二平差算法；Calikins[13]和Meid[14]則是通過對測量現(xiàn)場的不確定度進行研究，給出了一種基于光束平差法的誤差處理方法；何榮基基于間接平差原理，給出了自由設站測量時含約束條件的平差模型。但上述研究大多是針對單次測量或單級轉(zhuǎn)站所開展的，而對于船臺測量場構建時的多級轉(zhuǎn)站過程，相關的研究還相對較少。

為了對利用多級轉(zhuǎn)站方法構建船臺測量場時公共點的最優(yōu)坐標轉(zhuǎn)換參數(shù)進行求解，本文采用一種基于最小二乘原理和公共點經(jīng)過多級轉(zhuǎn)站后返回原站位坐標不變原則的聯(lián)合平差算法，并通過構建拉格朗日函數(shù)得到平差值的求解方法，實現(xiàn)了船臺測量場公共點位置誤差的最小化處理。通過模擬實驗，對此方法的有效性和精度進行了驗證。

1 誤差方程及其求解方法

1.1 誤差方程

根據(jù)誤差理論和測量平差原理[15-16]，在利用多級轉(zhuǎn)站方法構建船臺測量場時，公共點的殘余誤差方程可以寫為：

在轉(zhuǎn)站測量中，V為轉(zhuǎn)站后公共點坐標的誤差矩陣；A為 誤差方程的系數(shù)矩陣；為轉(zhuǎn)站參數(shù)誤差矩陣；L為公共點的經(jīng)過轉(zhuǎn)站后的坐標和測量坐標的偏差。

當轉(zhuǎn)站測量時公共點誤差最小時，V取最小值，同時，滿足最小值，式中，為公共點坐標的權值矩陣。

1.2 誤差方程的求解方法

由坐標轉(zhuǎn)換模型可知，在公共點由第j站轉(zhuǎn)至第j+1站時，有

式中：j和j+1分別公共點的坐標數(shù)據(jù)在第j站和第j+1站測量得到；kj，Rj和Tj分別代表公共點坐標從第j站轉(zhuǎn)至第j+1站時的尺度參數(shù)、角度參數(shù)和距離參數(shù)。其中，公共點在轉(zhuǎn)站前后相對位置不變，故kj取值為1，坐標轉(zhuǎn)換原理和歐拉角理論，角度參數(shù)可表示為Rj=RXj·RYj·RZj，對應角度分別為 αj，βj， γj，距離參數(shù)可表示為：

在船臺測量場中，對于某一個公共點在j+1站的坐標，其位置誤差可以表示為其真實坐標和測量值的差值，即

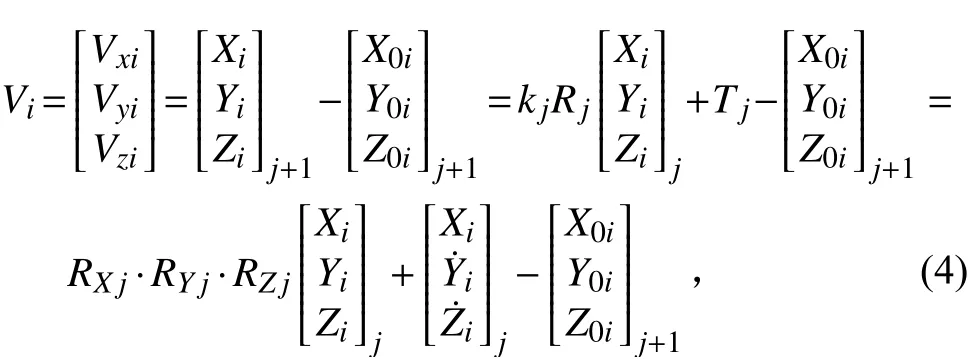
對式（4）作泰勒展開，并與式（1）聯(lián)立，可以得到：

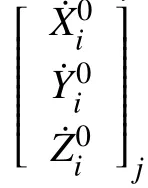
式中，為第i個公共點在第j站的測量坐標初值，分別為第i個公共點從第j站轉(zhuǎn)至第j+1站的平移參數(shù)，分別代表第i個公共點在第j+1站的真實坐標初值。

2 約束條件方程及其求解方法

2.1 約束條件方程

在轉(zhuǎn)站過程中，同時滿足公共點在第1站的坐標在經(jīng)過多次轉(zhuǎn)站后，當其轉(zhuǎn)回第1站時，坐標不變，即

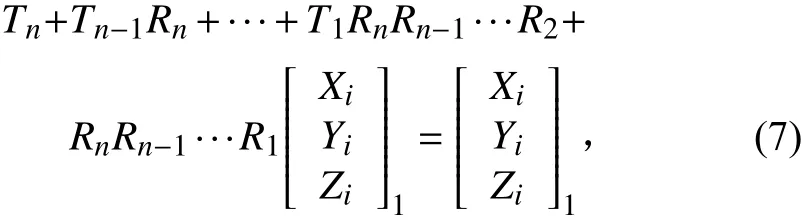
若式（7）成立，則有

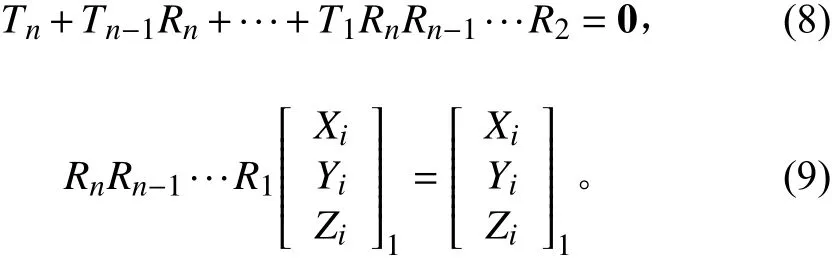
式（8）和式（9）即為約束條件方程。

2.2 約束條件方程的求解方法

在平差計算時，可將約束條件方程寫成如下形式：

對式（10）作泰勒展開，可得：

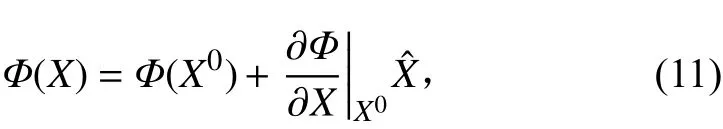
令

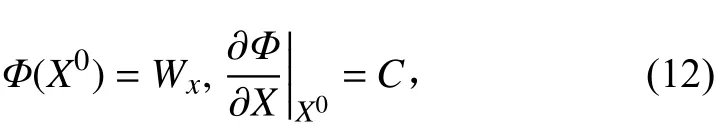
則式（12）可寫成如下形式：

文獻[17]對式（13）的線性化處理方法進行了詳細闡述，并得到了對應參數(shù)的具體表達形式。

3 平差值的求解方法

根據(jù)約束條件方程構建拉格朗日函數(shù)：

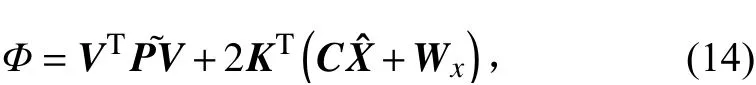
的參數(shù)矩陣。

求偏導，設此時 Φ的偏導數(shù)為零，則 Φ有極小值，即此時誤差最小，則

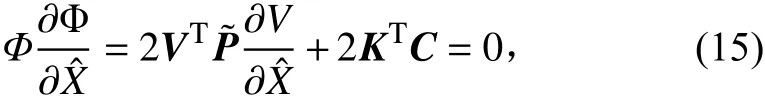
經(jīng)整理，可得：

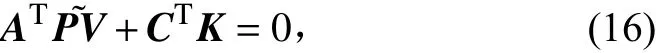
將式（1）代入，可得：

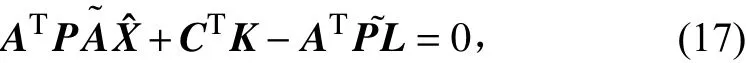
令

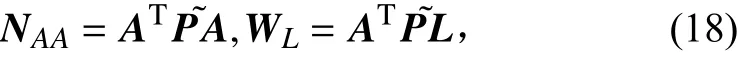
則式（18）可以寫成

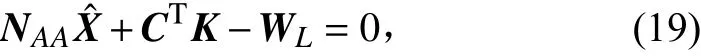
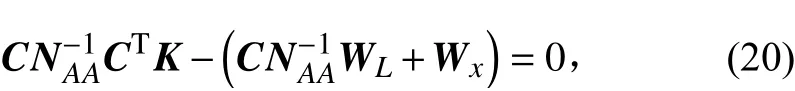
令

則式（20）可寫成

則有

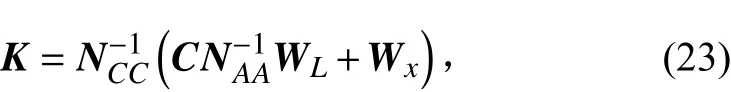
將式（23）代入式（18），可得：

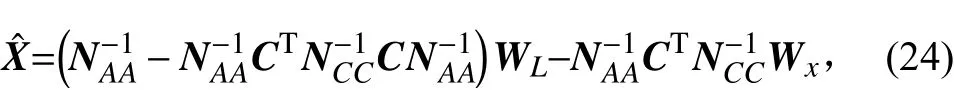
同時，未加約束條件的平差值經(jīng)整理，可以表示為：

4 實驗驗證

本次實驗在船臺測量場的基礎上，對確定公共點在基準坐標系中位置的轉(zhuǎn)站測量過程進行了模擬，對利用聯(lián)合平差算法對所測得的公共點坐標數(shù)據(jù)進行處理，并通過與未進行聯(lián)合平差的結(jié)果進行對比，對基于聯(lián)合平差的船臺測量場標定方法進行驗證。

4.1 實驗過程

1）在實驗場地內(nèi)的不同位置共布設22個公共點，在第1測量站位架設全站儀，為了對船臺測量場的實際情況進行模擬，各站位所測得的公共點數(shù)量均不相同，每個公共點測量10次。

2）將全站儀轉(zhuǎn)移至下一站位，重復過程1，直至測完6站，并對測量數(shù)據(jù)進行記錄。

4.2 實驗結(jié)果

在本次實驗中，采用每一測站下每個公共點10次測量數(shù)據(jù)的平均值作為當前站位的測量坐標，同時，將相鄰的兩站兩兩組合，利用坐標轉(zhuǎn)換算法對角度參數(shù)R和距離參數(shù)T進行計算，共得到6組數(shù)據(jù)。

利用聯(lián)合平差算法對測量數(shù)據(jù)進行處理，其中，平差初值為通過計算得到的6組坐標轉(zhuǎn)換參數(shù)，約束條件方程根據(jù)公共點在第1站的坐標進行一輪坐標轉(zhuǎn)換后返回第1站時與原坐標的差值最小列出，并設置迭代計算時角度閾值為1″，距離閾值為0.1mm。最后，將經(jīng)過聯(lián)合平差處理得到的中誤差和坐標轉(zhuǎn)換參數(shù)與未經(jīng)過聯(lián)合平差處理的數(shù)據(jù)進行對比。

表1為在經(jīng)過聯(lián)合平差計算前后，所用站位所測得的公共點經(jīng)過坐標轉(zhuǎn)換統(tǒng)一至第1站的坐標數(shù)據(jù)。表2和表3分別表示不同轉(zhuǎn)站過程的測量數(shù)據(jù)，在經(jīng)過聯(lián)合平差計算前后坐標轉(zhuǎn)換參數(shù)誤差的對比。從表中數(shù)據(jù)可以看出，公共點的測量數(shù)據(jù)經(jīng)過聯(lián)合平差計算后，其坐標轉(zhuǎn)換參數(shù)誤差整體小于聯(lián)合平差計算前的坐標轉(zhuǎn)換誤差。還可以看出，在進行聯(lián)合平差前后，其坐標轉(zhuǎn)換參數(shù)誤差的差值較小，這是因為在本次實驗中，每一站為所測的公共點數(shù)量較多，并且每個公共點的坐標值均是10次重復測量取平均得到，公

表1 聯(lián)合平差前后的公共點坐標Tab. 1 Coordinates of common points before and after joint adjustment

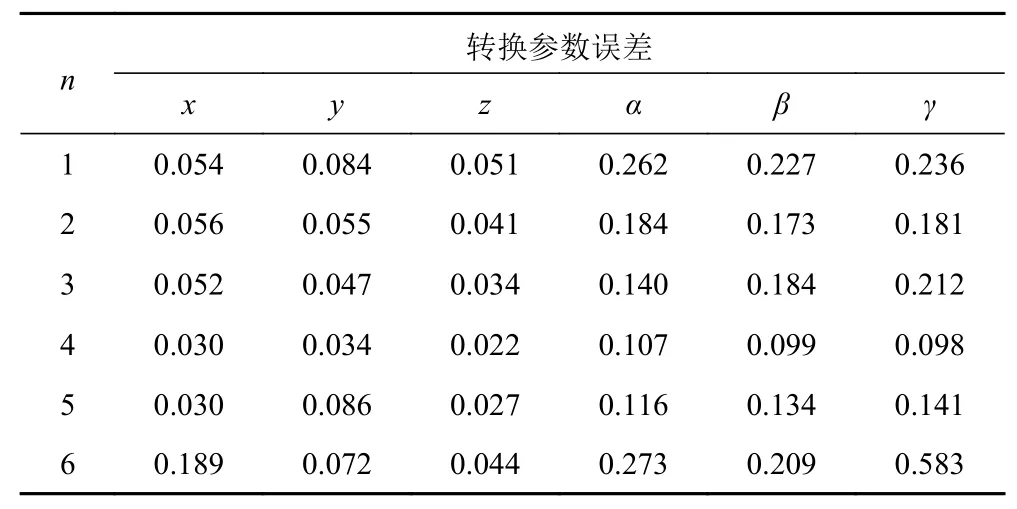
表2 未經(jīng)聯(lián)合平差的轉(zhuǎn)站參數(shù)誤差Tab. 2 Transformation parameter errors without joint adjustment

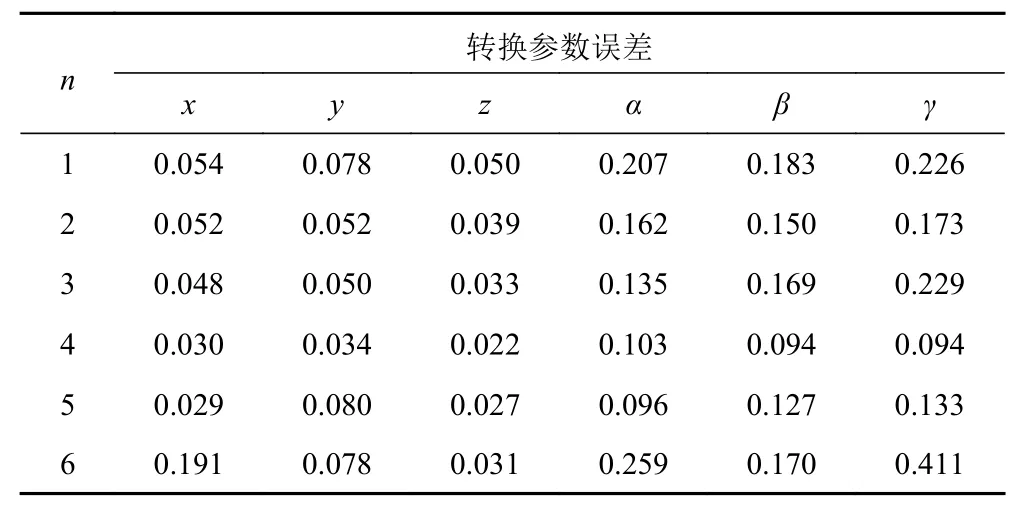
表3 聯(lián)合平差后的轉(zhuǎn)站參數(shù)誤差Tab. 3 Transformation parameter errors after joint adjustment

共點測量坐標本身所帶有的測量誤差較小，因此，坐標轉(zhuǎn)換參數(shù)誤差較小，其差值也較小。表4為在經(jīng)過聯(lián)合平差前后，第6站的公共點坐標在經(jīng)過一輪坐標轉(zhuǎn)換后，返回至第6站時的坐標與原坐標的差值，由表中數(shù)據(jù)可以看出，在經(jīng)過聯(lián)合平差之后，第6站公共的坐標經(jīng)過坐標轉(zhuǎn)換返回至第6站后與原坐標的差值更小，進一步說明了利用聯(lián)合平差算法對公共點坐標進行處理可以有效提升船臺測量的整體精度。

表4 聯(lián)合平差前后第6站的坐標差Tab. 4 Coordinate difference of 6th station before and after joint adjustment

5 結(jié) 語

在利用多級轉(zhuǎn)站的測量方法構建船測量場的過程中，由于公共點測量誤差和坐標轉(zhuǎn)換算法誤差的存在，會導致不同站位所測得的公共點坐標統(tǒng)一至基準坐標系后與其真實空間位置產(chǎn)生一定的偏差，從而影響船臺測量場的精度。本文采用聯(lián)合平差算法實現(xiàn)了多級轉(zhuǎn)站時最優(yōu)坐標轉(zhuǎn)換參數(shù)的求解，該方法基于最小二乘原理和誤差最小原則，給出了船臺測量場公共點經(jīng)過多級轉(zhuǎn)站測量的誤差方程及其求解方法，并根據(jù)公共點經(jīng)過坐標轉(zhuǎn)換返回原站位坐標不變的原則，給出了對應的約束條件方程及其求解方法。最后，根據(jù)拉格朗日函數(shù)，得到了平差值的求解方法。實驗證明，本文所提出的船臺測量場聯(lián)合平差標定算法有效減少了船臺測量場的誤差，提高了利用船臺測量場進行測量作業(yè)的精度。