全雙工多中繼網絡的中斷分析與中繼決策

江虹，辜馨月，楊浩

（西南科技大學 信息工程學院，四川 綿陽 621010）

在無線網絡通信中，由于環境的多徑效應、陰影衰落等影響，部分通信節點間的直連通信鏈路會變得不可靠，空間距離過遠的節點甚至可能無法直接進行通信.此外，隨著無線設備的普及和帶寬應用的不斷增加，移動數據流向呈現爆炸式增長，有限的頻譜資源愈發緊缺，無線網絡對提升通信速率、提高頻譜利用率的要求日益增強[1-2].近年來，為改善無線網絡的通信性能，緩解頻譜資源緊缺的現狀，全雙工無線中繼網絡（Full Duplex Wireless Relaying Networks，FD-WRNs）受到了廣泛關注.FD-WRNs 能在不提高節點發射功率的情況下擴大網絡通信范圍，有效提高頻譜利用率[3-6].然而，在FD-WRNs 網絡中，接收機的天線不僅會接收到其他發射機的干擾，還會接收到自身天線發送出的干擾，即節點自干擾[7-10].同時，在多中繼情況下，如果不能合理選擇中繼節點，有可能會導致網絡服務質量下降.

中斷概率是衡量無線通信系統的重要指標，為獲得更好的通信性能，許多學者在不同的網絡環境下對其展開了分析.Koc 等[11]和Nauryzbayev 等[12]在不考慮直達鏈路的情況下分別基于Nakagami-m 衰落和α-μ 衰落對全雙工中繼系統進行了中斷性能分析.Wang 等[13]在考慮直達鏈路和傳輸延時的情況下給出了放大轉發中繼策略下全雙工系統的中斷概率閉合表達式.Zhong 等[14]針對無線攜能通信系統（Simultaneous Wireless Information and Power Transfer，SWIPT），分析比較了解碼轉發與放大轉發兩種模式下中斷概率的性能表現.但上述文獻中涉及的通信系統模型皆為簡單的三點兩跳網絡（即包含一對通信的用戶節點與一個中繼節點），信號傳輸過程中不存在節點間互干擾和中繼決策的問題，而實際FD-WRNs 中通常需要從多個節點中選擇合適的中繼來完成輔助轉發的工作.

中繼節點的選擇是否合理在極大程度上影響著FD-WRNs 的網絡通信性能.Gu 等[15]提出了一種基于雙向拍賣的中繼選擇策略，以用戶節點能獲得鏈路容量提升和中繼節點轉發時需付出的能量分別作為出價和要價對傳統的拍賣模型進行修正，但分析時采用了正交信道，未考慮鏈路間干擾和距離衰落帶來的影響.Chen 等[16]對含有兩個混合接入點（Hybrid Access Points，HAPs）和多個中繼節點的全雙工多中繼網絡進行研究，文中假設只有被選擇的中繼從休眠模式切換到激活模式，在保證雙向通信鏈路服務質量的前提下進行中繼選擇；但該模型中同一時刻處在通信狀態的節點僅有HAPs 和被選擇的中繼節點，網絡中不含其他干擾.Wang 等[17]和Atapattu等[18]基于全局信道狀態信息（Channel State Information，CSI）給出了一種適用于全雙工中繼系統的最優中繼選擇（Optimal Relay Selection，ORS）方案，在考慮直達鏈路和自干擾的情況下，為了獲得更好的通信性能，利用CSI 選擇使鏈路信干噪比（Signal to Noise Interference plus Noise Ratio，SINR）最大的節點作為信息傳輸時的中繼節點.類似地，劉杰群等[19]利用局部CSI 在Rayleigh 衰落條件下提出了一種最小干擾信號（Minimize Interference Signal，MIS）中繼選擇算法，MIS 算法通過比較部分通信鏈路的信道衰落系數，從中選出衰落最小的路徑以保證信號衰落程度最小，進而降低信號傳輸的中斷概率和誤符號率，提升系統的通信性能.但ORS 算法和MIS 算法未考慮網絡中多用戶節點同時通信時鏈路間的互干擾對網絡性能造成的影響.

綜上所述，現有文獻中，為便于分析，在對FDWRNs 進行研究時大多僅考慮了節點數較少的簡單網絡或忽略網絡中部分干擾，然而實際通信中網絡構成往往更為復雜，且網絡中的干擾會極大程度上影響通信性能，使用簡單網絡模型或忽略部分干擾進行分析得到的結果可靠性較低.因此，本文針對節點自干擾與網絡聚集干擾同時存在的FD-WRNs 在Nakagami-m 衰落條件下分析其通信時的中斷性能，并提出了一種適用于全雙工多中繼環境下的中繼決策算法MCM 以降低網絡的中斷概率，提升通信系統的傳輸性能.與直接通過SINR 或干擾大小進行中繼決策的ORS 算法與MIS 算法不同，MCM 算法將根據每個用戶對中繼節點的需求決定網絡的中繼策略，最大化發揮網絡中每個中繼節點的作用.

1 系統模型

本文考慮含有M+N 個節點的無線網絡，同一時刻下，M 個節點作為通信的源節點或目的節點，稱為用戶節點，N 個節點為不能直接通信或直接通信性能不佳的用戶節點提供中繼服務，稱為中繼節點.用U、R 分別代表用戶節點集合和中繼節點集合，則有U={ui|i=1，…，M}，R={rj|j=1，…，N}.網絡中的節點皆為全雙工節點，具有激活與休眠兩個狀態，且僅在通信時處于激活狀態，其余時刻都處于休眠狀態，激活狀態的節點會對其他節點造成干擾.假設中繼節點工作在放大轉發模式，所有的通信鏈路都經歷獨立且相同分布的Nakagami－m 衰落.hp，q（p，q∈U∪R）為節點p 與q 之間的鏈路信道增益；Ip，q表示節點p與q 通信時，其他處于激活狀態的用戶節點與中繼節點在q 處形成的聚集干擾；分別為節點p 處的自干擾與自干擾消除系數，其中，的值為節點p的發射功率，βp=1 代表未消除自干擾，βp=0 代表自干擾完全消除；dp，q為節點p 與q 之間的距離；ηp，q為節點p 與q 通信過程中的加性高斯白噪聲（Additive White Gaussian Noise，AWGN），ηp，q～CN（0，σ2）.

現考慮網絡中任意兩個用戶節點ux與uz進行通信（x≠z，ux、uz∈U），如圖1 所示.圖中ry（ry∈R）為ux、uz采用中繼轉發方式進行通信時選用的中繼節點，R′=R{ry}，U′=U{ux，uz}分別為其他中繼節點和用戶節點對uz或ry形成的聚集干擾集合.

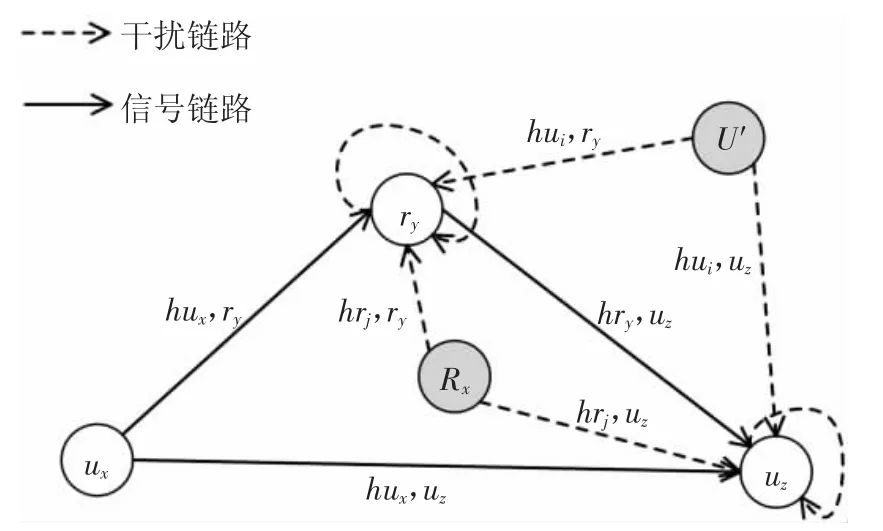
圖1 ux 與uz 通信時的FD－WRNs 模型Fig.1 FD－WRNs model when ux communicate with uz

假設所有的節點都以功率Pt發射信號.當用戶節點ux與uz以直達鏈路進行通信時，uz處的SINR可表示為：

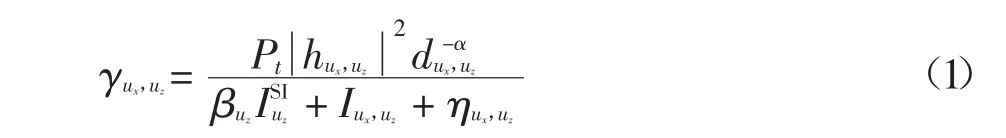
式中：α ＞2 為路徑損耗系數.此時其他節點在uz處形成的聚集干擾Iux，uz可表示為：

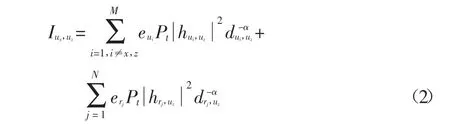
式中：eui=1、erj=1 分別代表用戶節點ui、中繼節點rj發送信號，即節點處于激活狀態；反之，eui=0、erj=0 代表用戶節點ui、中繼節點rj不發送信號，節點處于休眠狀態.

同理，在放大轉發模式下，當ux與uz通過節點ry中繼輔助進行通信時，中繼節點ry與用戶節點uz處的SINR 分別如式（3）和（4）所示：

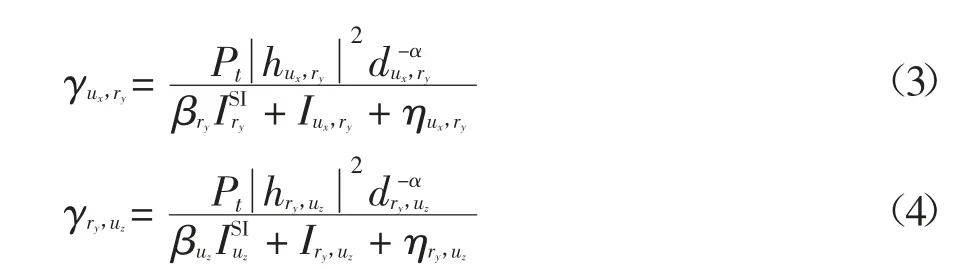
其中，聚集干擾項Iux，ry和Iry，uz可分別表示為：

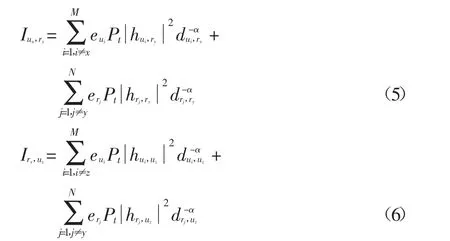
放大轉發模式下，協作通信傳輸的信干噪比可表示為[15]：

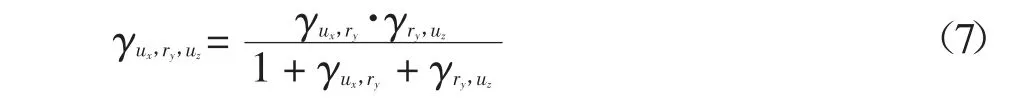
令A∈{（ux，uz），（ux，ry），（ry，uz）}，鏈路信道增益的概率密度函數（Probability Density Function，PDF）可表示為[14]：

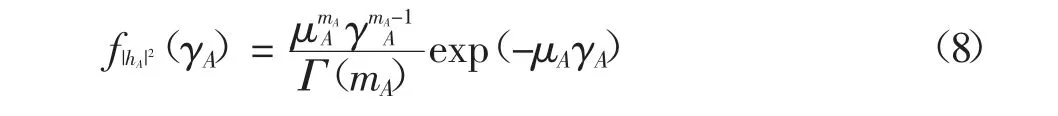
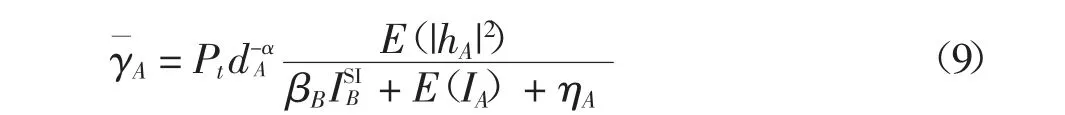
式中：B∈{ry，uz} 對應著通信時接收信號的節點.A=（ux，ry）時B 為ry，A 為其他取值時B 為uz.由式（2）（5）和（6），聚集干擾項的均值E（Iux，uz）、E（Iux，ry）和E（Iry，uz）可分別表示為：

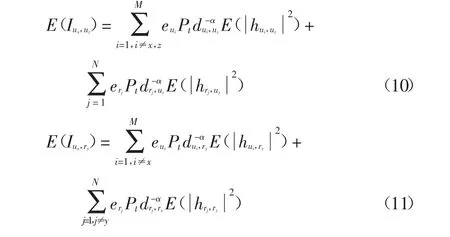
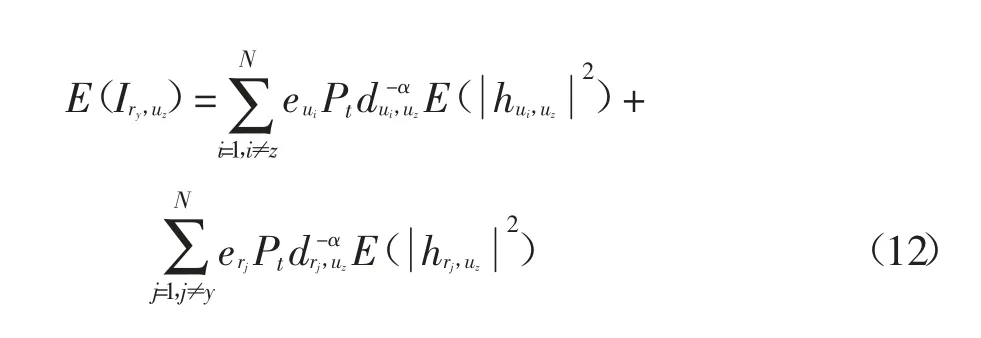
2 中斷性能分析與中繼決策

2.1 中斷性能分析

在圖1 所示通信場景中，假設成功通信需滿足的最低信干噪比閾值為γth，用戶節點ux與uz以直達鏈路通信時的中斷概率可表示為：

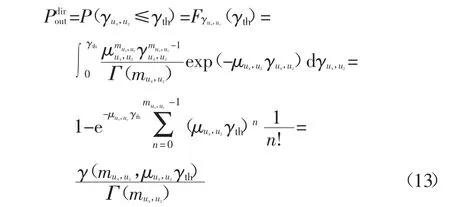
式中：Fγux，uz（·）為γux，uz的分布函數（Cumulative Distribution Function，CDF）為不完全Gamma 函數.

計算ux與uz通過ry中繼輔助進行通信時的中斷概率.由于式（7）分母中的常數項1 對通信性能影響很小，特別是在高SINR 環境下，即γux，ry、γry，uz＞＞1時，其影響幾乎可忽略不計[20-21].因此式（7）可表示為：

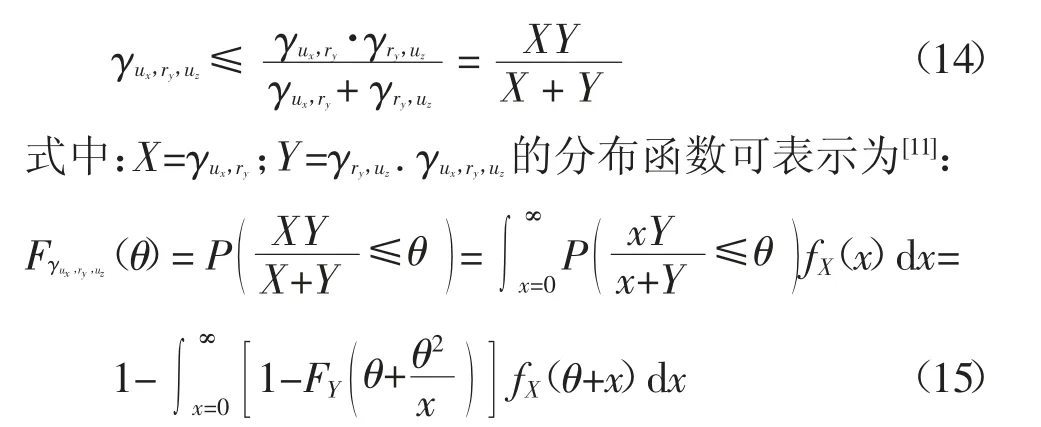
類比式（13），Y 的分布函數可表示為：

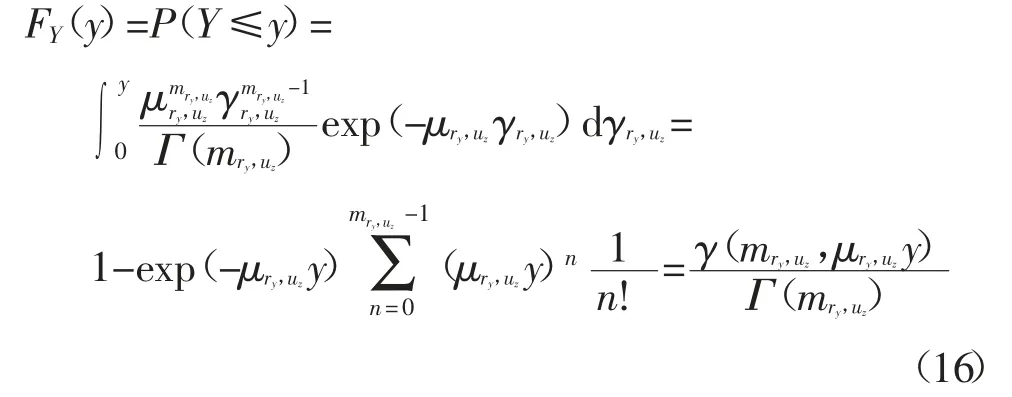
結合式（8）（15）（16），有

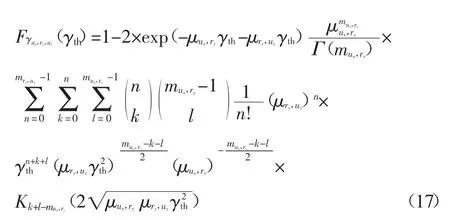
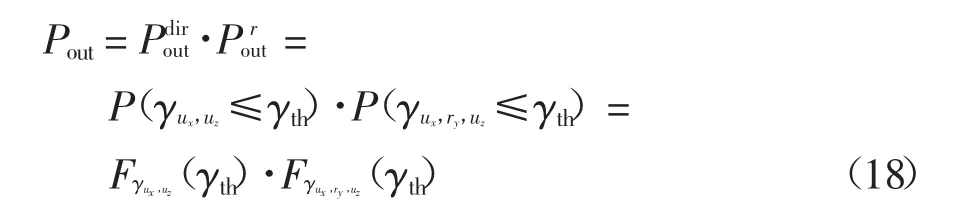
將式（13）（17）代入式（18），可得中斷概率的具體表達式.

2.2 中繼決策

當無線網絡中存在多個中繼節點時，某個中繼節點可能同時滿足多個用戶節點的需要，但同一時刻單個中繼節點能服務的用戶節點數目是有限的.這種“多選一”的情況下，中繼節點為誰提供服務會影響到整個網絡的性能.此部分將以最小化系統中斷概率為目的提出MCM 算法為用戶節點分配中繼.

假設每個中繼節點同時只能為單個用戶節點提供服務，在全雙工模式下，用戶節點ux與uz可能同時向對方發送信號，此時若只有一個中繼為ux與uz之間的通信提供服務，由于該中繼同一時刻只能轉發一個傳輸方向的信號，將會導致來自另一個傳輸方向的信號依然無法被目的端正確接收.因此，對于全雙工模式下無法直接通信或直接通信效果不佳的用戶節點ux與uz，應為二者各自分配一個中繼節點.由于最小化網絡中斷概率與最大化網絡成功傳輸概率等價，所以中繼決策問題可轉化為：

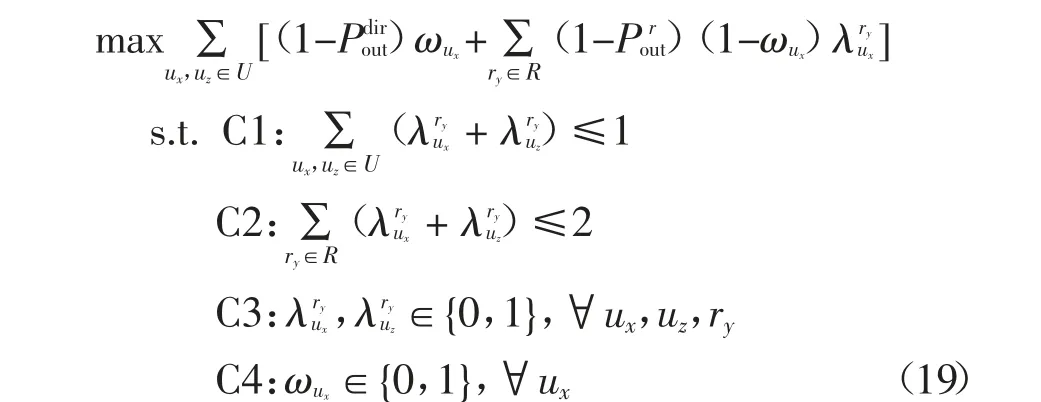
式中：ωux代表用戶節點ux與其目的用戶節點uz采用的通信方式.若ωux=1，則ux與uz通過直達鏈路通信；若ωux=0 則通過中繼輔助通信.表明中繼節點ry為用戶節點ux提供服務.約束條件C1 表示一個中繼節點只能為U 中的一個用戶節點提供服務.約束條件C2 表示每個用戶節點最多只能被分配一個中繼，若不等式取值為2 則意味著當前通信雙方各自選擇一個中繼輔助通信；為0 則表示通信雙方直接通信.約束條件C3 表明某個用戶節點與某個中繼節點之間的狀態只有1 和0 兩種，即該中繼節點是否為該用戶節點提供服務.約束條件C4 表明用戶節點之間有直達與中繼輔助兩種通信方式.

為了減少中繼節點的資源浪費，最大程度發揮每個中繼節點的作用，本文為每個用戶節點設定其對中繼節點的渴求度δ，根據渴求度進行網絡中繼決策.δ 具體值取決于該用戶節點到目的節點直達鏈路的中斷概率，將用戶節點的渴求度與該用戶節點通過中繼輔助方式通信時的成功概率相乘，其乘積作為此用戶參與分配中繼時的優先級.對于任意用戶節點ux，直達鏈路的中斷概率越高意味著該節點越需要中繼節點的輔助來完成與目的用戶節點uz的通信，即相應的渴求度δux越大.當中繼成功概率相同時，渴求度越高的用戶節點越有可能被分配到中繼節點.反之，當渴求度相同時，用戶節點會被分配到通信成功概率更高的中繼節點.通過上述方法優化U 中每個用戶節點的通信方式，即可使整個通信系統的中斷概率最小.用戶節點ux對中繼節點的渴求度計算方式定義如下：

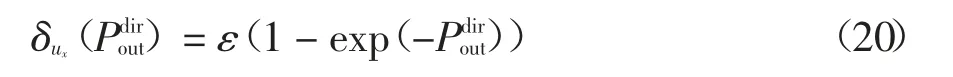
借助圖論知識，可通過構建二部圖將式（19）轉化為最大帶權匹配問題后用Kuhn-Munkres 算法進行求解.若僅在進行通信的節點之間建邊則會出現孤點，因此為保證Kuhn-Munkres 算法順利運行，本文通過構建權值為0，即不具備競爭力的虛擬邊將FD-WRNs 中的通信場景構建為二部圖.MCM 算法的細節如下：首先，用U 和R 中的節點構建二部圖中的頂點集.隨后，在U 中的每個用戶節點與R 中的每個中繼節點之間補充虛擬邊，將邊權設置為0建圖.最后，對于直達鏈路中斷概率大于中繼鏈路中斷概率的用戶節點，將此用戶節點與相應的中繼節點之間的邊權更新為渴求度與中繼鏈路成功概率的乘積.由此，利用Kuhn-Munkres 算法可求解出該二部圖的最大帶權匹配.算法1 描述了MCM 算法的流程.

3 數值仿真分析

通過蒙特-卡羅仿真和數值仿真在不同的Nakagami-m 信道衰落參數、自干擾消除系數和信干噪比閾值條件下，對比分析無干擾網絡情景和有干擾網絡情景內中斷概率隨節點發射功率的變化情況并對MCM 算法的有效性進行驗證，仿真100 次.取FD-WRNs 的用戶節點數M=12，中繼節點數N=10，網絡中的節點均勻分布且坐標經歸一化處理.假設所有用戶節點都處于激活狀態，即eu=1，?u∈U，中繼節點的狀態服從伯努利分布.對于所有的仿真測試，通信過程中的AWGN 強度為σ2=1，路徑損耗系數α=4，信道鏈路增益ry），（ry，uz）}）.

圖2 展示了γth=0 dB，β=0.05 時，不同mA取值條件下中斷概率隨節點發射功率的變化情況.由圖2可知，mA取值越大，中斷概率越小.當mA取值相同時，同一發射功率下，無干擾的信道（僅考慮噪聲）較有干擾的信道具有更低的中斷概率.當節點的發射功率不斷增大時，由于網絡中的自干擾和聚集干擾也不斷增大，因此，有干擾的信道條件下系統的中斷概率逐漸減小后在發射功率達到20 dB 左右后開始趨于穩定，而無干擾的信道條件下的中斷概率不斷降低.

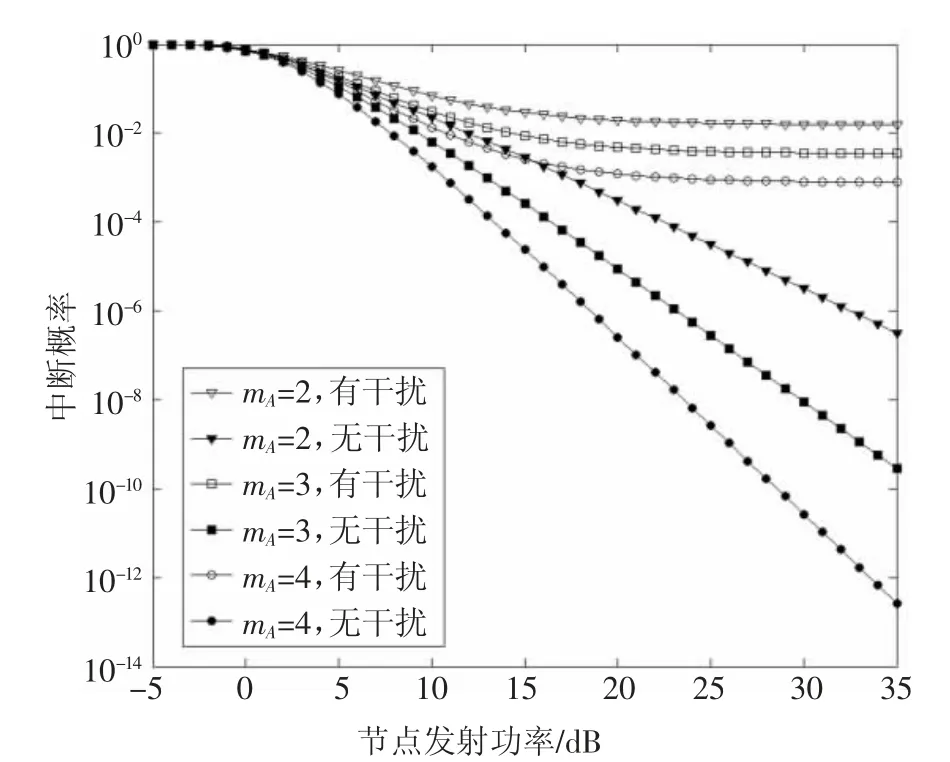
圖2 mA 取值不同時中斷概率隨發射功率的變化圖Fig.2 Trend of outage probability with the transmit power for different value of mA

圖3 為β=0.2，mA=2 時，不同γth取值條件下中斷概率隨節點發射功率的變化情況.分析圖3 可以發現，系統的信干噪比閾值越高，中斷概率相對越大.當節點的發射功率增加到20 dB 左右時，系統的中斷概率會趨于穩定，此后發射功率的提升并不會改善系統的中斷性能.

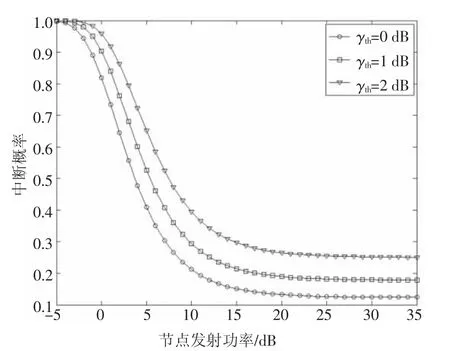
圖3 γth 值不同時中斷概率隨發射功率的變化圖Fig.3 Trend of outage probability with the transmit power for different value of γth

圖4 展示了γth=0 dB，mA=2 時，不同β 取值條件下中斷概率隨節點發射功率的變化情況.從圖4可以看出，無論β 取值如何，中斷概率都會隨著節點發射功率的增大而減小，最后在發射功率達到15 dB左右時趨于穩定.當β 取值相同時，有聚集干擾場景下的網絡中斷概率高于無聚集干擾時的中斷概率.此外，如果不消除節點自干擾（β=1 時），即使不斷加大節點發射功率，系統仍具有較高的中斷概率.

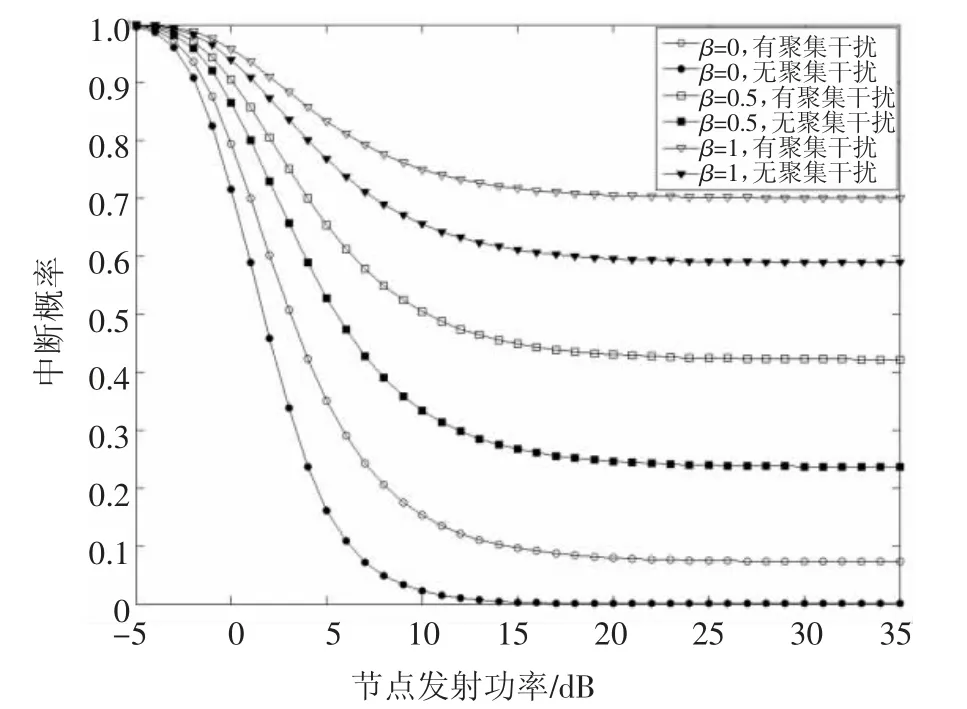
圖4 β 值不同時中斷概率隨發射功率的變化圖Fig.4 Trend of outage probability with transmit power for different value of β

圖5 為β=0.03，mA=2，γth=1 dB 的條件下，分別采用MCM 算法、MIS 算法和ORS 算法進行中繼決策后系統通信的中斷概率隨節點發射功率提升的變化情況.從圖中可以看出，發射功率提升至約25 dB，即發射功率對中斷概率的改善作用達到飽和狀態時，MCM 算法較MIS 算法和ORS 算法具有更低的中斷概率.經數值分析發現，此時采用MCM 算法得到的系統中斷概率比采用ORS 算法低約4%，比采用MIS 算法低約7%.

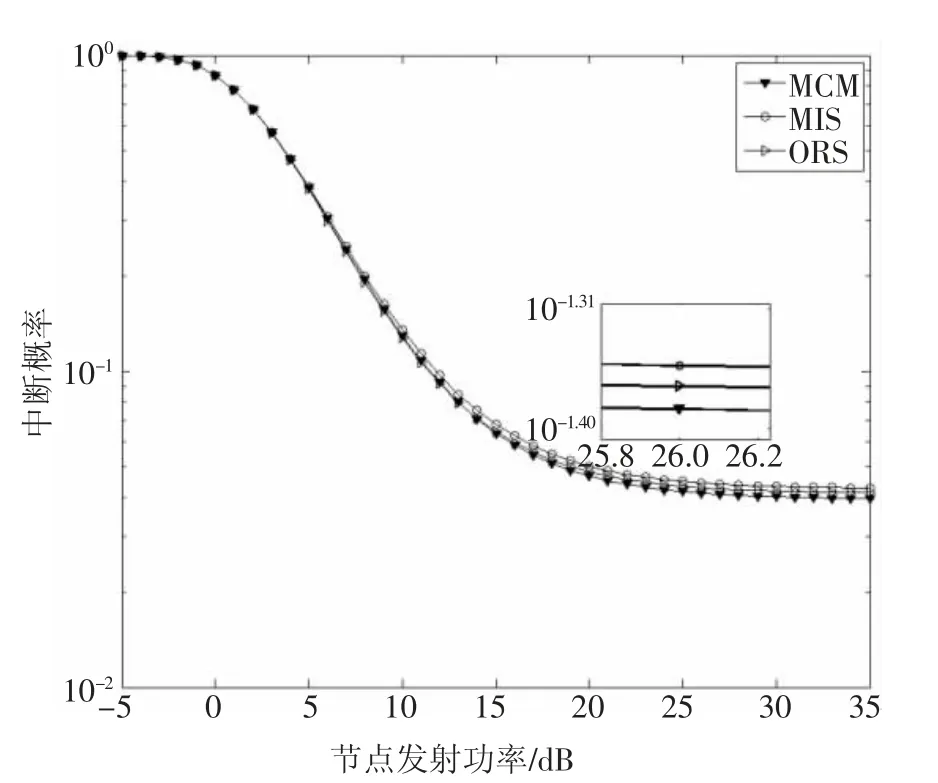
圖5 3 種算法下FD-WRNs 的中斷概率變化Fig.5 Outage probability change of FD-WRNs under three algorithms

由于MCM 算法是基于Kuhn-Munkres 算法解決最大帶權匹配問題，故二者在算法性能上表現類似.而Kuhn[22]指出Kuhn-Munkres 算法復雜度為O（n3），對于二部圖總能求解出其最大帶權匹配結果.因此，Kuhn-Munkres 算法保證了MCM 算法得到的中繼決策方案是全局最優的，但求解過程中需要完備的CSI，且當網絡規模較大時，受算法復雜度影響，決策過程耗時較長，節點能耗也會相應增加.

4 結論

針對自干擾與聚集干擾同時存在的FD-WRNs網絡通過蒙特-卡羅法仿真了不同系統參數下中斷概率隨節點發射功率的變化情況，并對比分析了MCM 算法與其他中繼選擇算法在改善系統中斷性能方面的效果，得出以下主要結論：

1）提升節點的發射功率能在一定程度上降低通信的中斷概率，但當發射功率達到某一特定值后，加大發射功率對網絡中斷性能帶來的改善作用將會趨于飽和.

2）在FD－WRNs 中，自干擾對無線通信的中斷性能影響極大，若不進行自干擾消除，即使提升節點發射功率至飽和狀態，系統仍具有極大的中斷概率.

3）同一仿真環境下，采用MCM 算法能夠為通信系統帶來更低的系統中斷概率.當增加發射功率對系統中斷概率的提升效果達到飽和后，采用MCM 算法得到的系統中斷概率比ORS 算法和MIS 算法降低了約4%～7%.

4）通過MCM 算法雖然能得到當前網絡中最優的中繼方案，但網絡規模較大時，算法復雜度和CSI 獲取過程為網絡節點帶來的能耗壓力也不容忽視，該問題將在今后的研究中進行優化.