網絡能量在混合圖中的研究與應用
劉勝久,李天瑞?,謝鵬,劉佳
(1.西南交通大學 信息科學與技術學院,四川 成都 611756;2.四川省云計算與智能技術高校重點實驗室,四川 成都 611756)
圖能量最早是由Gutman 于1978 年正式提出的[1],對圖能量的研究可溯源到二十世紀三四十年代化學家對共軛的烴類化合物總π 能量的研究.烴類化合物總π 能量可通過Huckel 分子軌道理論近似求出[2-3].圖能量定義為圖的鄰接矩陣所有特征值絕對值之和.自圖能量提出以來,圖能量受到人們極大的關注,一系列能量,如距離能量[4]、擬Laplacian能量[5]、關聯能量[6]、匹配能量[7]、Laplacian 能量[8]、無符號Laplacian 能量[9]、Von Neumann 能量[10]、距離Laplacian 能量[11]、距離無符號Laplacian 能量[11]等其他類似能量,相繼提出.
圖能量自提出以來已在理論化學及代數圖論等領域得到極為廣泛的應用,一些重要研究成果相繼問世.由于大規模矩陣特征值計算極為繁瑣,對圖能量的研究更多的集中在隨機圖、正則圖、樹圖、二部圖等幾類特殊的圖中[12-14].對圖能量的改進與拓展是圖能量研究的重要內容,一系列類似能量的提出大大豐富了圖能量的研究內容.但這些類似能量仍未脫離鄰接矩陣特征值計算的局限,應用范圍受限.現今提出的圖能量及類似能量已有數十種之多[15],對圖能量的研究已由無向圖推廣應用到有向圖[16-17]、混合圖[18-20]等其他多種類型的圖.由于混合圖節點之間連接的復雜性,對混合圖能量的研究遠較無向圖及有向圖復雜[21-22],實際上,對圖能量的研究目前仍以對無向圖的能量研究為主,并改進后逐步推廣應用到有向圖及混合圖等[23].
先前,本文作者從網絡維數[24]的視角出發,提出了網絡能量的概念,將網絡能量應用于無向圖[25]及有向圖[26],并將無向圖的網絡能量與傳統意義上的圖能量及距離能量、擬Laplacian 能量、關聯能量、匹配能量等進行對比,得出了一些有意義的結論,同時將有向圖的網絡能量與無向圖的網絡能量及有向圖的斜能量等進行對比,也得出了一些有意義的結論.本文中,我們嘗試將網絡能量由無向圖及有向圖推廣應用到混合圖,并分析研究混合圖網絡能量的若干重要性質.
1 預備知識
1.1 圖能量

式中:λ1A(G)、λ2A(G)、λ3A(G)、…、λiA(G)、…、λnA(G)表示A(G)的各個特征值.
對無向圖G 的所有邊賦予一個方向σ,則得到一個有向圖Gσ,其斜鄰接矩陣可記為S(Gσ).有向圖Gσ中,若節點vi與vj之間存在一條有向邊,則Aij=-Aji=1,否則,Aij=Aji=0.有向圖Gσ的斜能量εS(Gσ)定義為其斜鄰接矩陣S(Gσ)的所有特征值絕對值之和,即[16]

式中:λ1S(Gσ)、λ2S(Gσ)、λ3S(Gσ)、…、λiS(Gσ)、…、λnS(Gσ)表示S(Gσ)的各個特征值.
由于對無向邊賦予一個方向有兩種不同的選擇,一個無向圖G 對應有2m個有向圖Gσ.圖的大部分類似能量均基于矩陣特征值的計算,如距離能量、擬Laplacian 能量、關聯能量等.對大規模矩陣而言,特征值計算極為困難,使得精確的圖能量分析殊為不便,圖能量只在極少數的特殊圖中得到較為深入的分析研究.對圖能量的研究更多的是關注圖能量的上下限,如對正則圖及隨機圖能量上限的研究等.
1.2 網絡能量
由于傳統意義上的圖能量依賴于對矩陣特征值的計算,對大規模圖的應用受限,人們嘗試從其他的途徑得到圖能量,以避免對矩陣特征值計算的低效操作.我們從網絡維數的視角出發,提出了網絡能量的概念.
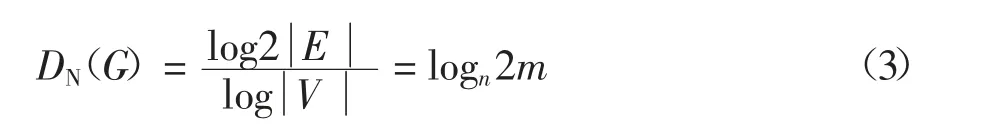
圖G 的網絡能量EN(G)定義為[23]:

圖G 的網絡能量EN(G)與圖G 的能量E(G)二者之間有許多類似的性質,并且存在多個共同的上限.與無向圖的分析研究類似,對無向圖G 的所有邊賦予一個方向而得到的有向圖Gσ而言,其網絡維數DN(Gσ)可以表述為:

圖Gσ的網絡能量EN(Gσ)定義如下[24]:

圖Gσ的網絡能量EN(Gσ)與圖G 的網絡能量EN(G)及圖Gσ的斜能量ε(Gσ)三者之間存在極為密切的關聯.對比式(4)及式(6),可以發現,EN(G)與EN(Gσ)二者之間有著相似的形式,可以對它們進行深入細致的分析.
1.3 混合圖
混合圖M 是對無向圖G 的部分邊賦予一個方向而得到的圖.對任一混合圖M 而言,其Hermitian鄰接矩陣可記為H(M).混合圖M 中,若節點vi與vj之間存在一條有向邊,則Hij=-Hji=i;若節點vi與vj之間存在一條無向邊,則Hij=Hji=1;若節點vi與vj之間不存在任何邊,則Hij=Hji=0.混合圖M 的Hermitian 能量εH(M)定義為其Hermitian 鄰接矩陣H(M)的所有特征值絕對值之和,即[18]
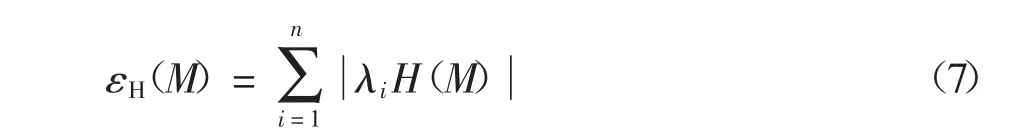
式中:λ1H(M)、λ2H(M)、λ3H(M)、…、λiH(M)、…、λnH(M)表示H(M)的各個特征值.
對混合圖而言,還有Hermitian-Randic 能量[19]、Hermitian 關聯能量[20]等其他多種形式的能量.
混合圖M 的Hermitian 能量εH(M)也有很多與無向圖G 的圖能量E(G)及有向圖Gσ的斜能量εS(Gσ)等類似的上下限.
對含有n 個節點m 條邊,且原始圖中節點最大度為Δ 的混合圖M 來說,其Hermitian 能量εH(M)上下限滿足下式[18]:
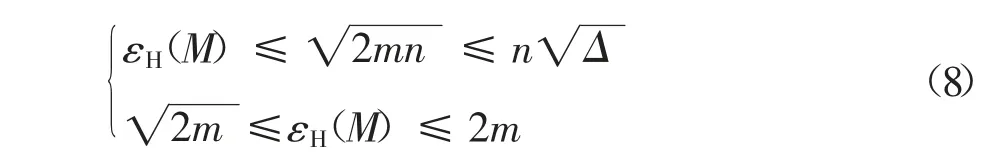
對比無向圖G 的圖能量E(G)及有向圖Gσ的斜能量εS(Gσ)的上限,很顯然,混合圖的Hermitian 能量εH(M)兼具E(G)及εS(Gσ)的一些特點.
特別地,當混合圖M 的原始圖為k-正則圖時,有

可以發現,混合圖的Hermitian 能量具備無向圖的網絡能量的一些特點.
由于混合圖遠較無向圖及有向圖復雜,對混合圖能量的研究尚在持續深入,相關的研究成果并不多.
對比式(1)(2)(7)可以發現,無向圖、有向圖、混合圖的能量計算均是通過計算矩陣的特征值而得到的,計算復雜.通過式(3)對無向圖的網絡維數的研究,提出了無向圖的網絡能量;通過式(5)對有向圖的網絡維數的研究,提出了有向圖的網絡能量.同理,對適用于無向圖及有向圖的網絡維數進行拓展,將網絡維數應用于混合圖中,提出混合圖的網絡能量.
2 混合圖的網絡能量研究
2.1 混合圖的網絡維數
混合圖既含有無向邊,又含有有向邊,是一類介于無向圖與有向圖之間的特殊的圖.通過對式(3)中無向圖的網絡維數及式(5)中有向圖的網絡維數的研究,可以得出混合圖的網絡維數.

混合圖M 的網絡維數DN(M)可以表述為:

由于混合圖M 是對無向圖G 中的部分無向邊賦予方向而得到的,若賦予有向邊的比例為r,即

式(11)可改寫為:

對式(11)進行分析,可以發現,當r=0 時,混合圖M 退化為無向圖G,此時,式(13)退化為式(3);當r=1 時,混合圖M 退化為有向圖Gσ,此時,式(13)退化為式(5).即式(3)所示的無向圖的網絡維數及式(5)所示的有向圖的網絡維數分別是式(13)所示的混合圖的網絡維數在r=0 及r=1 時的特例.于是,通過式(13)將無向圖、有向圖、混合圖三者通過網絡維數聯系起來了.
2.2 混合圖的網絡能量
觀察式(4)及式(6),可以發現,無向圖及有向圖的網絡能量均是通過其對應的網絡維數式(3)及式(5)得到的,對式(11)所示的混合圖的網絡維數進行研究,可以得到混合圖M 的網絡能量EN(M),如式(14)所示:

對式(14)進行分析,可以得到等價的另一表述,如式(15)所示:

對式(15)進行分析,可以發現,當r=0 時,混合圖M 退化為無向圖G,此時,式(15)退化為式(4);當r=1 時,混合圖M 退化為有向圖Gσ,此時,式(15)退化為式(6).即式(4)所示的無向圖的網絡能量及式(6)所示的有向圖的網絡能量分別是式(15)所示的混合圖的網絡能量在r=0 及r=1 時的特例.于是,通過式(15)將無向圖、有向圖、混合圖三者通過網絡能量進一步聯系起來了.
2.3 不同類型圖的網絡能量
式(3)(5)(13)分別給出了無向圖、有向圖、混合圖的網絡維數,對這些公式進行分析,可以得出它們之間的關系.
對式(3)及式(5)進行分析,可以得到:

對式(3)及式(13)進行分析,可以得到:

在實際計算中,只要得到有向圖、無向圖、混合圖三者之一的網絡維數及混合圖中有向邊的比例r,即可得到另外二者的網絡維數.
式(4)(6)(15)分別給出了無向圖、有向圖、混合圖的網絡能量,對這些公式進行分析,可以得出它們之間的關系.
對式(4)及式(6)進行分析,可以得到:
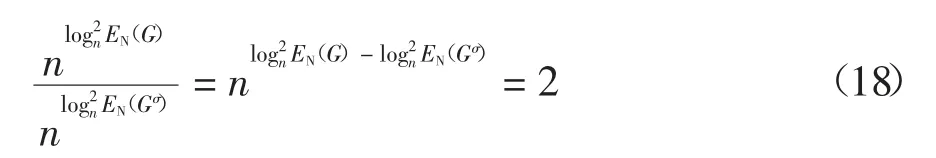
對式(4)及式(13)進行分析,可以得到:
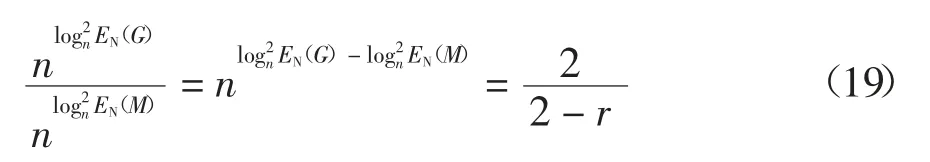
于是,在實際計算中,只要得到有向圖、無向圖、混合圖三者之一的網絡能量及混合圖中有向邊的比例r 與節點數目n,即可得到另外二者的網絡能量.
3 混合圖的網絡能量性質
上文中通過對無向圖及有向圖的網絡維數及網絡能量的分析研究,提出了混合圖的網絡能量,下面,我們對混合圖的網絡能量性質進行分析研究.
定理1 混合圖M 的網絡能量EN(M)介于其原始圖G 的網絡能量EN(G)及有向圖Gσ的網絡能量EN(Gσ)之間,即

證 根據定義,定理1 顯然成立.定理1 得證.證畢.
根據定理,可以得出混合圖M 的網絡能量EN(M)的上限不超過原始圖G 的網絡能量EN(G)的上限,混合圖M 的網絡能量EN(M)的下限不低于有向圖G 的網絡能量EN(Gσ)的下限,即EN(G)的上限也是EN(M)的上限,EN(Gσ)的下限也是EN(M)的下限.
式(20)取等號的條件是無向圖G、有向圖Gσ、混合圖M 均為空圖,即三者均只含有節點,不含有邊,即,此時,有
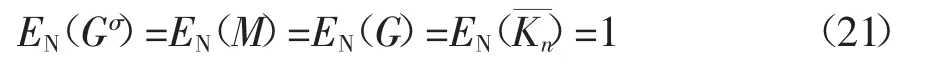
于是,可以得出如下引理.
引理1 混合圖M 的網絡能量EN(M)的下限為1,即

證 根據定義,引理1 顯然成立.引理1 得證.證畢.
引理1 的結論可以推廣應用到無向圖及有向圖中.實際上,無向圖G 的網絡能量EN(G)及有向圖G的網絡能量EN(Gσ)的下限均是1.
下面,對混合圖M 的網絡能量EN(M)的上限進行分析研究.
定理2 混合圖M 的網絡能量EN(M)的上限滿足式(23):
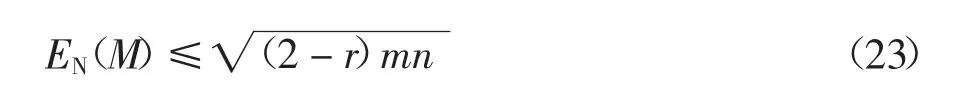
式中:n 為混合圖M 的節點數目;m 為混合圖M 的邊數目;r 為混合圖M 中有向邊的比例.
證 根據式(15)所示的混合圖網絡能量的表述,欲證定理2,只需證式(24)即可:


定理2 顯然成立.定理2 得證.證畢.
當r=0 及r=1 時,定理2 的結論也可以推廣應用到無向圖及有向圖中.由于0 定理3 混合圖M 的網絡能量EN(M)的上限滿足式(27): 式中:n 為混合圖M 的節點數目;m 為混合圖M 的邊數目;r 為混合圖M 中有向邊的比例. 證 由于2m≤n(n-1),代入式(23),定理3 顯然成立.定理3 得證.證畢. 繼續對混合圖M 的網絡能量EN(M)的上限進行分析研究,可以得到EN(M)的一個更為緊致的上限. 定理4 當(2-r)m ≥n 時,混合圖M 的網絡能量EN(M)的上限滿足式(28): 式中:n 為混合圖M 的節點數目;m 為混合圖M 的邊數目;r 為混合圖M 中有向邊的比例. 證 根據式(15)所示的混合圖網絡能量的表述,欲證定理4,只需證明下式即可: 當且僅當x=n 時,f(x)的一階導數f′(x)=0. 于是,有 定理4 顯然成立.定理4 得證.證畢. 當r=0 及r=1 時,定理4 的結論同樣可以推廣應用到無向圖及有向圖中. 下面,對正則圖進行分析研究. 定理5 當混合圖M 的原始圖G 是k-正則圖時,混合圖M 的網絡能量EN(M)的上限滿足下式: 式中:n 為混合圖M 的節點數目;r 為混合圖M 中有向邊的比例;k 為原始圖G 中任一節點的節點度. 證 在原始圖G 中,由于G 是k-正則圖,則有kn=2m,即 將式(34)代入式(23),即有: 定理5 顯然成立.定理5 得證.證畢. 由于0 在特殊情況下,當G≌Cn,即G 是一個環圖時,有k=2,此時,可得到如下引理. 引理2 當混合圖M 的原始圖G 是一個環圖,即G≌Cn時,混合圖M 的網絡能量EN(M)的上限滿足下式: 證 將k=2 代入式(33),即得到式(36).引理2顯然成立.引理2 得證.證畢. 此外,當G≌Kn,即G 是一個完全圖時,有k=n-1,此時,可得到如下引理. 引理3 當混合圖M 的原始圖G 是一個完全圖,即G≌Kn時,混合圖M 的網絡能量EN(M)的上限滿足下式: 引理3 顯然成立.引理3 得證.證畢. 當r=0 及r=1 時,定理5 的結論及引理2、引理3 同樣可以推廣應用到無向圖及有向圖中. 下面對隨機圖進行分析研究. 定理6 當混合圖M 的原始圖G 是隨機圖Gn(p)時,混合圖M 的網絡能量EN(M)的上限滿足下式: 式中:n 為混合圖M 的節點數目;r 為混合圖M 中有向邊的比例;p 為原始圖G 中節點對之間隨機連接的概率. 證 在原始圖G 中,由于G 是隨機圖Gn(p),則有: 將式(40)代入式(23),即有: 定理6 顯然成立.定理6 得證.證畢. 從式(41)可以看出,當p=2/n 時,G 為一個環圖,此時,定理6 退化為引理2;當p=1 時,G 為一個完全圖,此時,定理6 退化為引理3.即定理6 是引理2 及引理3 在一般情形下的泛化與推廣. 當r=0 及r=1 時,定理6 的結論同樣可以推廣應用到無向圖及有向圖中. 無向圖的圖能量定義為圖的鄰接矩陣所有特征值絕對值之和.由于無向圖的圖能量在理論化學及代數圖論中的重要價值,圖能量自提出以來受到人們極大的關注,一系列的類似能量相繼提出,并逐步推廣應用到有向圖及混合圖等其他多種類型的圖.大多數圖的能量均是基于矩陣特征值計算得到的,如無向圖的距離能量、有向圖的斜能量、混合圖的Hermitian 能量等.由于大規模矩陣的特征值計算極為繁瑣,傳統意義上對圖能量的研究不便于推廣應用到大規模圖中.網絡能量脫離了傳統意義上圖能量基于矩陣特征值計算的局限,并在無向圖及有向圖中得到較為成功的應用.本文將應用于無向圖及有向圖中的網絡能量推廣到混合圖中,論述了混合圖的網絡能量,并分析研究了混合圖的網絡能量的若干重要性質.后續工作的重點在于對特定的混合圖的網絡能量進行分析,并嘗試對帶權圖、無限圖、超圖等更為復雜的不同類型圖的能量進行深入研究.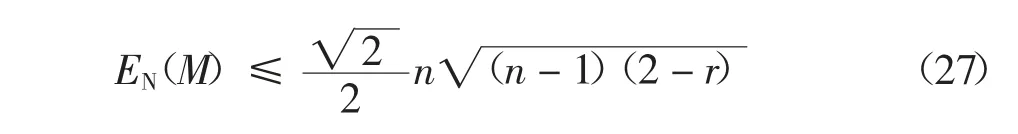
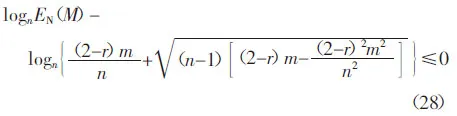

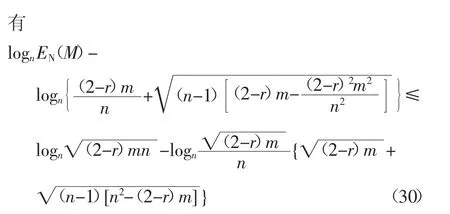

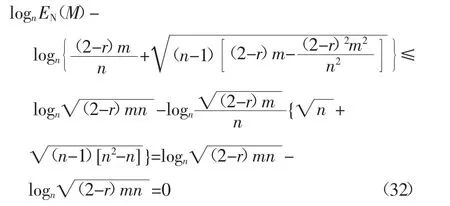


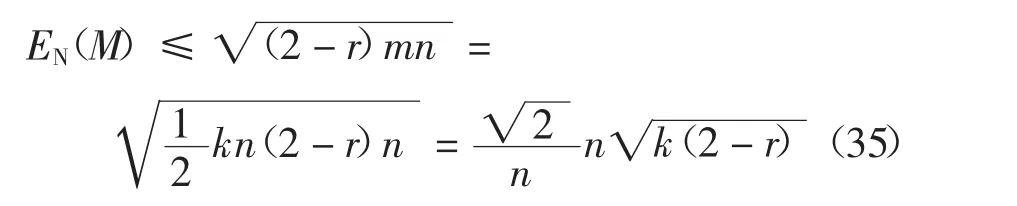

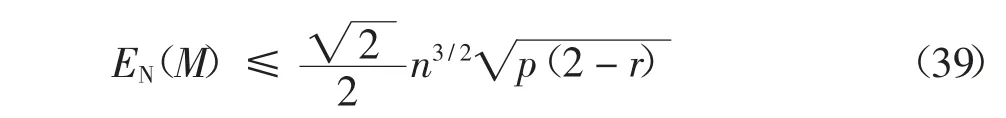


4 結論

