多傳感器融合技術在船舶液位監測中的應用

劉江莉，宮尚軍，張 磊，朱志松，姚興田

(南通大學 機械工程學院，江蘇 南通 226019)

0 引 言

船舶液位監控系統是實現船舶自動化的一個重要系統，關系到船舶在裝卸貨及航行中的安全問題。船舶在裝卸貨物的過程中，船體會發生一定程度的傾斜，為了保證船舶的平衡，需要對壓載水艙內的液位進行調節。工作人員根據壓載水艙的液位以及船舶的吃水狀態計算出相應的配載，手動控制或者自動控制壓載水泵和閥門的開啟狀態，對壓載艙進行壓水和排水[1]。液位監控系統自動化的應用節省了勞動力，提高了船員操作效率。高精度的液位監測系統則是船舶裝卸和航行安全的重要保證。因此，液位監測系統的首要問題是如何使測量的液位更精確、更可靠。

在液位監測的過程中，由于環境的不確定因素干擾以及單傳感器自身的局限性，使得測量的液位值往往不完整或帶有較大的不確定性，甚至含有異常噪聲點。針對液位測量的誤差，本文提出一種基于卡爾曼濾波的多傳感器融合算法，對液位測量值進行濾波，提高液位測量的精度，獲得了穩定可靠的輸出值。

1 液位監控系統

1.1 液位監控系統的結構

船舶液位監控系統主要由信號采集單元、下位機PLC、閥門控制單元、上位機監控軟件以及歷史數據庫組成。信號采集單元中的傳感器用于對艙內液位、吃水深度、壓力、溫度等參數進行采集。本系統的PLC 選用西門子S7-1 200，用于對多個傳感器采集的信號進行運算處理，根據不同的數據類型輸出相應的信號。閥門控制單元根據PLC 發出的命令，由閥門和壓載泵完成對應的動作。上位機選用組態王6.55 進行開發，采用TCP/IP 協議通過交換機與下位機進行通訊，并動態監控整個系統。歷史數據庫由MySQL 數據庫設計開發，采用ODBC 協議與上位機連接。圖1 為系統的結構圖。

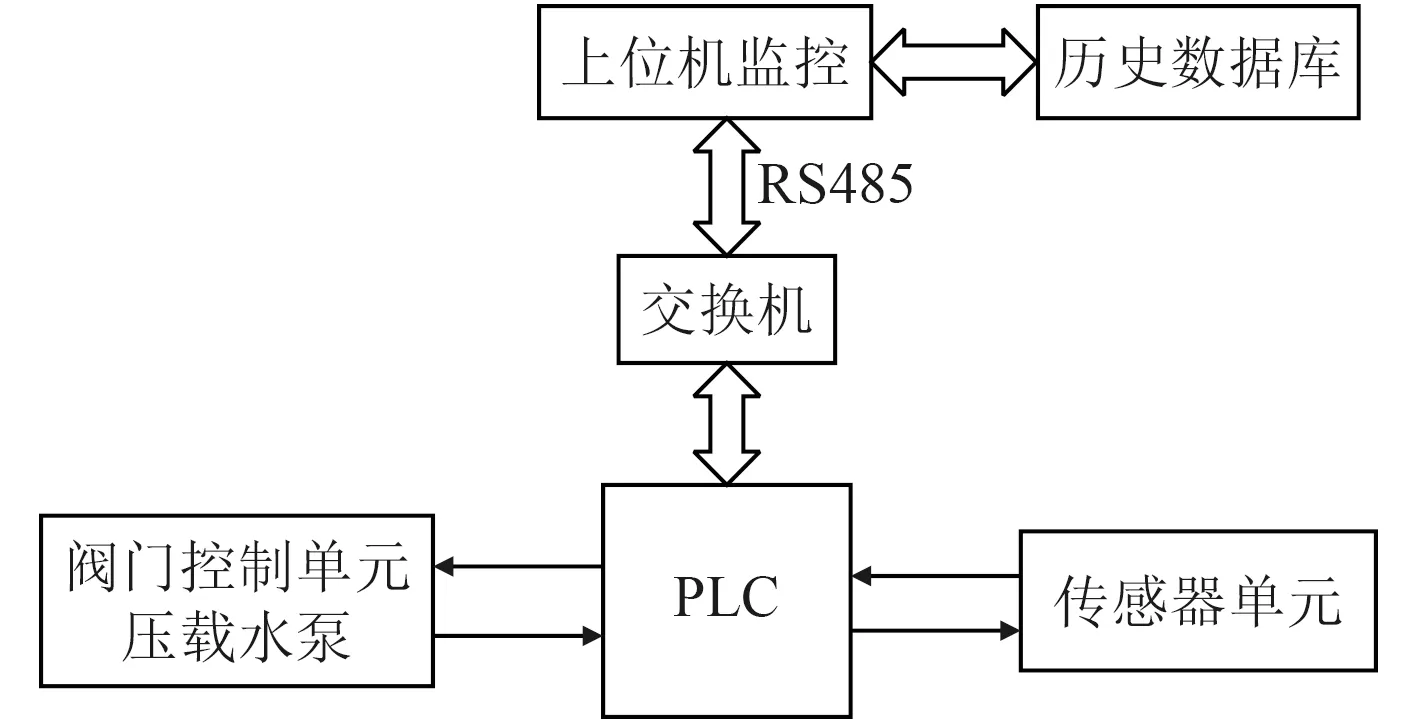
圖1 液位監控系統結構簡圖Fig.1 Structure diagram of liquid level monitoring system

1.2 液位測量的原理

船舶液位監控系統實時監測各壓載艙內液位的高度以及吃水深度，通過監測艙內液位的變化從而調控壓載系統的進排水量。因此，只有保證船舶吃水和壓載艙內液位等參數的精度及可靠，才能確保船舶實現準確、安全及平穩的控制。

船舶吃水測量的方法由傳感器的安裝方位決定。本文采用六角吃水測量法，將傳感器分別安裝在船舶左右兩舷的首中尾6 個角，左右吃水的測量由安裝在船舯左右舷底部壓載艙底的傳感器測得，首尾吃水的測量由安裝在首尖艙和隔離空艙底的傳感器測得[2]。船舶的橫傾角通過船左右吃水差得出，方法如圖2 所示。

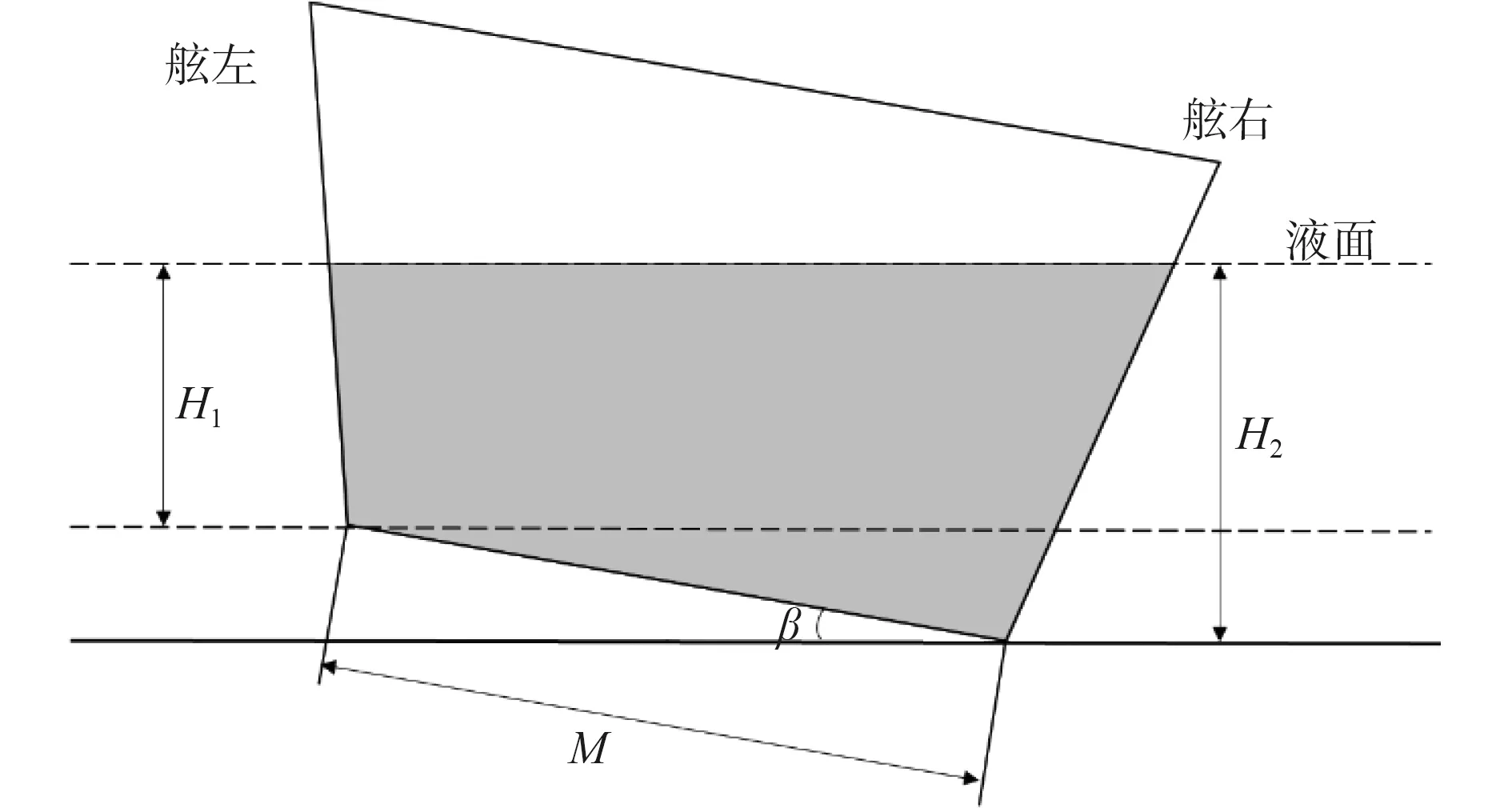
圖2 船舯左右吃水橫傾角計算Fig.2 Calculation of the yaw angle around the ship

圖中H1為 船中左側液位的高度,H2為船中右側液位的高度，M為船中左右兩側的液位傳感器測量的水平距離，船舶的橫傾角β的計算方法如下式：

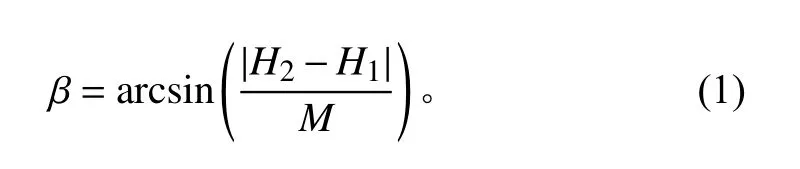
船舶縱傾角度的計算方法同理。從上述公式可看出船舶橫縱傾角度計算的真實值取決于船舷吃水測量的精度。

2 液位監測的誤差分析

船舶液位監測過程中，對液位的測量會不可避免地出現誤差，改進測量方法消除誤差則是液位監測系統中重要的一環。對測得的數據比較分析后發現，液位測量誤差的來源有2 個方面，一是傳感器設備產生的誤差，二是測量環境的不確定因素帶來的誤差。

傳感器在傳感器單元中，受到供電電路的電磁、電纜信號等干擾，可能會產生靜態性偏差、零點漂移及靈敏度漂移等問題，因而傳感器的初始標定值存在一定的誤差，需要對傳感器進行預處理，作二次標定以補償其新增不確定度[3]。

2.1 傳感器標定

針對液位傳感器的預處理流程如圖3 所示，包括標定、轉換、分值濾波和微值濾波幾個過程。

圖3 數據的預處理過程Fig.3 Data preprocessing

圖中XIN為輸入值，KX為 比例系數偏移，Z為零點偏移，CvSn為轉換值。

對傳感器在不同情況下測得的幾組數據進行標定[4]。在實驗水艙中，采用雷達液位計對0.5 m 高的液位進行測量，其電流輸出值為5 mA；對0.8 m 高的液位進行測量，輸出值為5.6 mA。標定公式如下式：

對標定后的轉換值CvSn，進行峰值或微值濾波處理[5]。峰值濾波指對超過設定峰值（DP）的變化值忽略。微值濾波則是對小于設定不靈敏區的值（AP）不做處理。

通過對傳感器進行預處理，可將測量誤差降至最低，也能減少部分測量過程中的隨機誤差，且對傳感器輸出值進行標定，也能及時檢測傳感器故障，提高傳感器測量輸出數據的可靠性。

2.2 波動液位的卡爾曼濾波

環境的因素則是由于船舶受到風浪的干擾以及在裝卸貨物時船體的傾斜導致液面的波動幅度較大，使得測得的誤差較大。

考慮到液面的波動是無法避免的，因此，需要對測得的液位信號進行濾波，將影響液位監測的液面波動、觀測噪聲等濾除，實時獲得精確可靠的液位監測。在中央處理單元采用濾波程序對采集的數據進行處理，本文采用卡爾曼濾波器對傳感器測量結果進行濾波，卡爾曼濾波是基于貝葉斯定理，利用遞歸迭代進行濾波的方法，主要用來預測和更新。

由卡爾曼濾波原理，隨機線性離散系統的方程為：

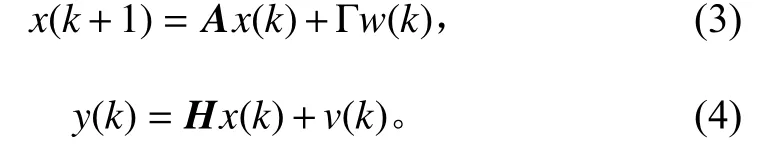
式中：x(k)為 系統的狀態向量；A為 狀態轉移矩陣；y(k)為觀測真值；H為觀測矩陣；w(k)，v(k)分別為過程噪聲和觀測噪聲[6]。

壓載系統對艙內液位高度進行調節，操控壓載泵和閥門對水艙內進水，記采樣時間為t0，s(k)為液位在采樣時刻kt0處的高度，記在時刻kt0處的液位速度為s˙(k)，由動力學公式：

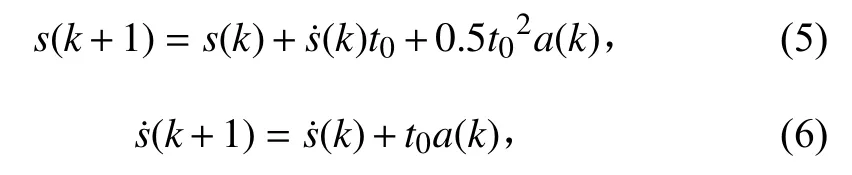
定義在采樣時刻kt0處 系統的狀態x(k)為液位的高度和速度，可得到液位高度的狀態方程為：

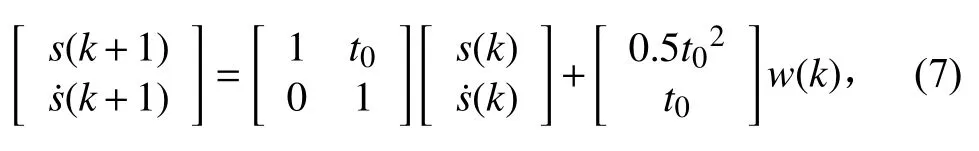
觀測方程為：

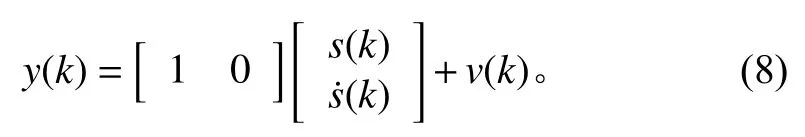
式中：w(k)∈Rm為過程噪聲，即由海風和海浪等不確定因素引起的隨機加速度，v(k)∈Rm為傳感器的觀測噪聲，且都是高斯白噪聲，均值為零,方差矩陣分別為Qk和Rk。

液位的預測過程為：

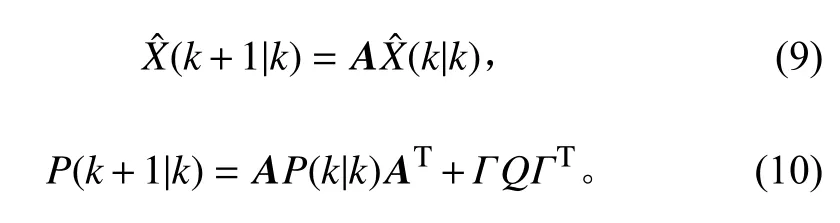
根據液位的預測方程，將液位的初始狀態以及初始協方差輸入卡爾曼濾波器后，可不斷得到液位變化的真實值，濾波效果理想[7]。

雖然傳感器測得的液位高度經過卡爾曼濾波后能夠得到一個較為穩定、精確的值，但在實際船舶液位監測的過程中，傳感器測得的液位數據在傳輸交換過程中不僅有可能出現時滯，且單個傳感器在液位測量的過程中可能會出現故障或者受到干擾導致得到的液位測量值與真實值相差較大。因而在本實驗系統中需采用多傳感器測量液位[8]，以減少信息處理過程中可能出現的偏差，提高液位估計精度，在對艙內液位建模時還需將液位監測系統作為時滯系統進行處理。

3 液位監測系統中的多傳感器融合算法

多傳感器融合算法作為智能測量的關鍵技術之一，其融合方式有多種，本文采用分布式融合算法，如圖4所示。首先單個傳感器測得的數據經過局部濾波器進行處理，得出各個傳感器的狀態估計值，然后采用最小二乘估計對估計狀態進行融合。分布式融合估計改變了全局最優估計的數據處理結構，將整個系統分成幾個小系統進行處理，提高了計算機實時并行處理速度[9]。

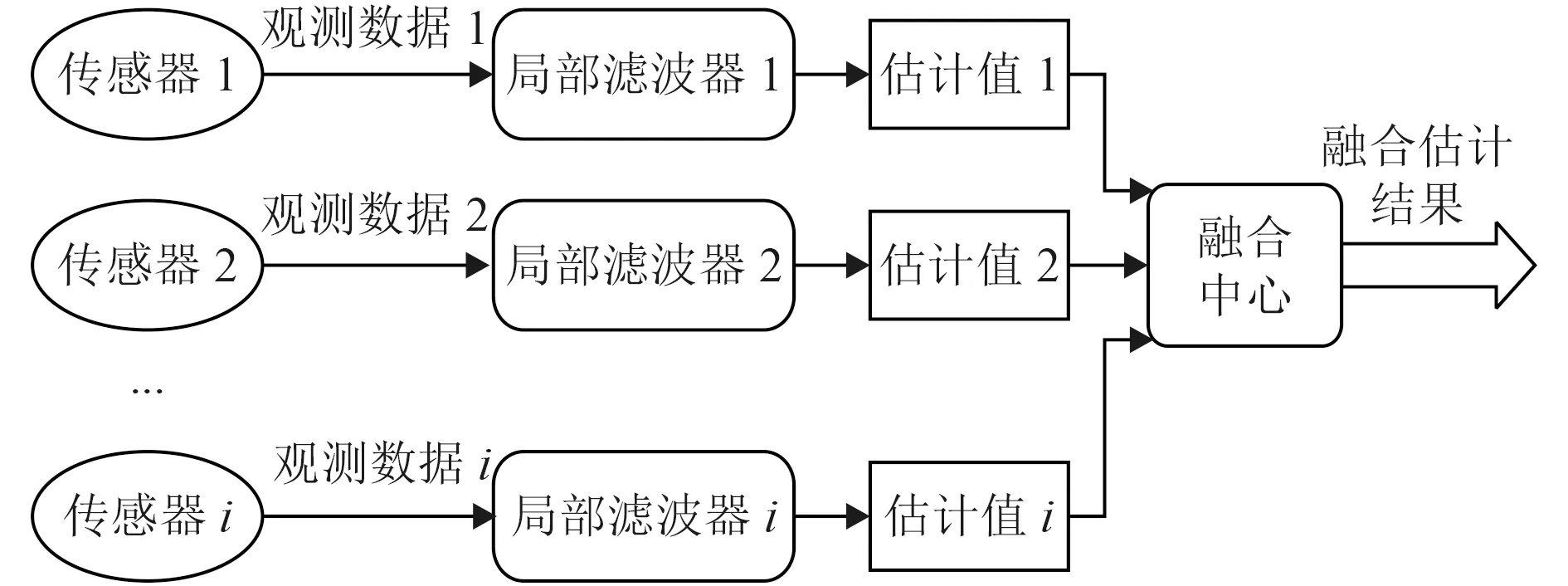
圖4 分布式融合算法結構圖Fig.4 Structure diagram of distributed fusion algorithm

3.1 多傳感器時滯系統

考慮傳感器測量的液位值在觀測中存在一步隨機時滯的非理想情況[10]，多傳感器線性離散系統模型如下：

式中：k為離散時間；x(k)∈Rn為液位狀態向量；r為系統本身的延遲時間；yi(k)∈Rm為第i個傳感器的液位觀測；w(k)∈Rm為過程噪聲，即由海風和海浪等不確定因素引起的隨機加速度，vi(k)∈Rmi為第i個傳感器的觀測噪聲，且都是高斯白噪聲，均值為零,方差矩陣分別為Qk和Rk；A,hi為 已知的維數矩陣；L表示傳感器的個數[8]。

采用二維隨機變量 εki(k＞1) 表示在k時刻第i個傳感器的觀測數據yi(k) 是否到達狀態估計器[11]；εki取值0 或1，服從伯努利分布，且滿足分布特性：

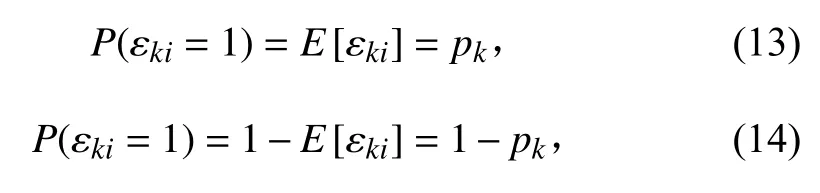
假設系統狀態x0和噪聲wk，vk均不相關；wk和vk相互獨立。

對系統狀態擴展，狀態擴展形式：

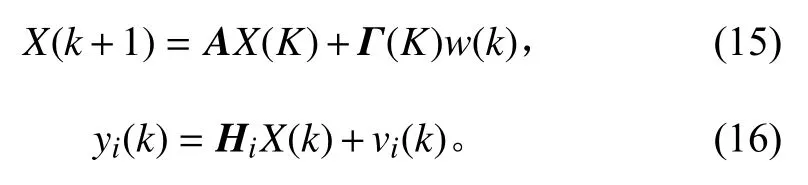
式中：A，Γ，Hi為常矩陣；(A,Hi) 完全可觀，且A為穩定矩陣。

3.2 最優加權融合卡爾曼濾波器設計

卡爾曼濾波的過程主要為預測與更新，在k時刻，數據正確到達濾波器時，液位狀態的估計值與誤差方差應取根據誤差推得的更新值；當新的觀測數據由于時滯無法到達時，需要的液位狀態的估計值與誤差方差應取上一時刻的預測狀態和預測誤差方差[12]。

1）第i個傳感器的局部最優卡爾曼濾波

2）任意2 個傳感器之間的估計誤差互協方差

預測互協方差：

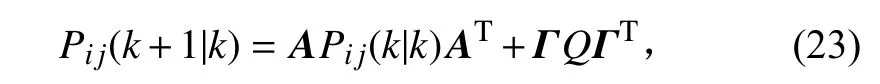
更新互協方差：

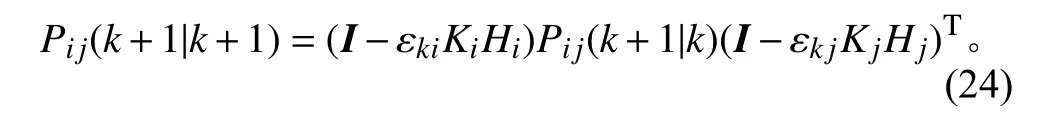
式中：i,j=1,2,···,L；I為單位矩陣；εk為0 或1 的隨機值。

3）多傳感器分布式加權最優融合估計

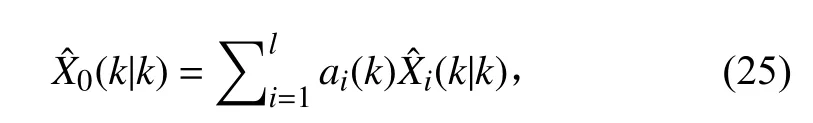
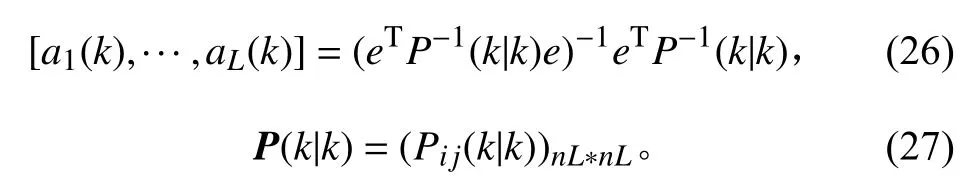
式 中：eT=[In,···,In]；P(k|k)是Pij(k|k) 第 (i,j)元素的nL*nL分塊矩陣。

最優融合誤差陣：

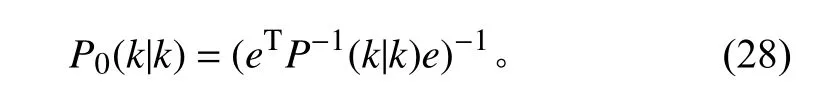
在實驗中將液位的初始高度以及液位變化的初始速度賦值給初始狀態，給出估算的初始協方差，輸入并啟動最優卡爾曼濾波器即可得到穩定且精確的真實液位值[13]。

4 實驗仿真及結果分析

在實驗室內模擬船舶的壓載艙設計實驗水艙，實現液位監測系統的功能并采集水艙進出水時液位的數據，進行算法處理，輸出液位的精確值[14]。船舶裝卸貨物時，壓載艙根據船舶的傾斜角度調節相應壓載艙的艙內液位。在本文實驗中，將調節壓載水前的液位高度作為初始高度值，將水泵抽水的速率轉換成液位上升高速度。對一側水艙內的液位的測量采用2 個雷達液位計進行觀測，在水艙晃動的情況下分別做進水處理和無進出水處理。

在Matlab 中進行仿真，首先在實驗水艙液位不變的情況下，只對其做晃動處理，取80 個采樣點。液位高度初始值為0.512 m，且由式（17）～式（22）可求得單傳感器的局部狀態最優卡爾曼估計值，如圖5 和圖6 所示，即單傳感器在不同位置測得的數據的卡爾曼濾波。由式（25）得到分布式的矩陣加權最優融合估計，如圖7 所示。

由圖5～圖7 可得，傳感器測得的實時液位值上下波動，與實際值的誤差較大，而雷達液位計經過卡爾曼濾波器處理過的估計值趨于真實值，且較為穩定；而單傳感器測得的數據過于片面，不能全面表現出整個艙內的液位。從濾波融合估計值來看，波動基本處于實際液位值0.512 m 的±4 mm 左右，能準確表達艙內液位的狀態。

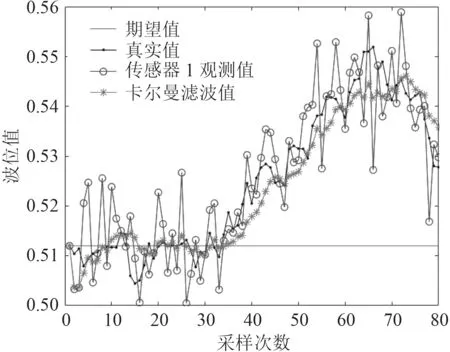
圖5 傳感器1 的液位測量值與濾波值Fig.5 Sensor 1 level measurement and filtered value

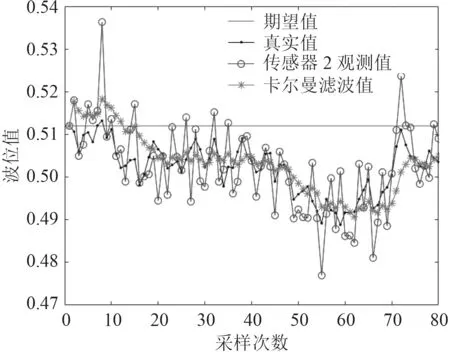
圖6 傳感器2 的液位測量值與濾波值Fig.6 Sensor 2 level measurement and filtered value

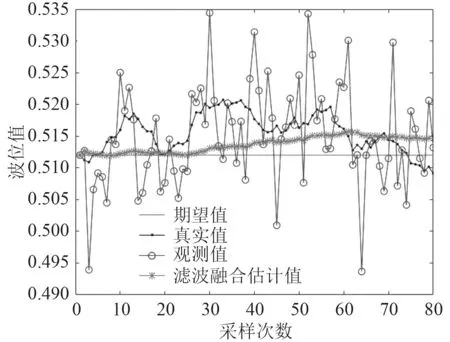
圖7 分布式加權融合卡爾曼濾波Fig.7 Distributed weighted fusion Kalman filtering

在實驗水艙進水時對水艙做晃動處理，取100 個采樣點，液位高度初始值為0.512 m，仿真結果如圖8～圖10 所示。

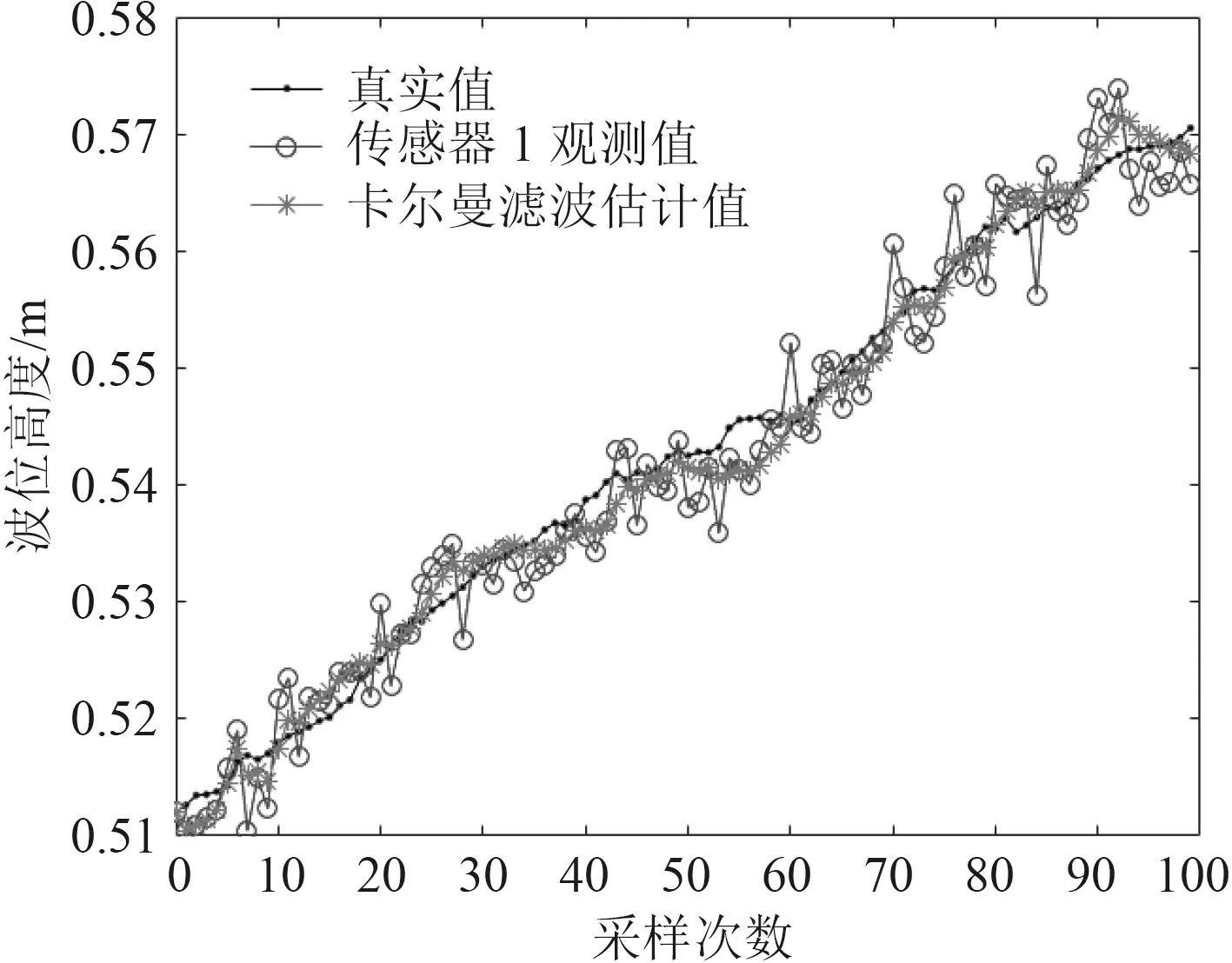
圖8 傳感器1 的測量值與濾波值Fig.8 Sensor 1 measured and filtered values

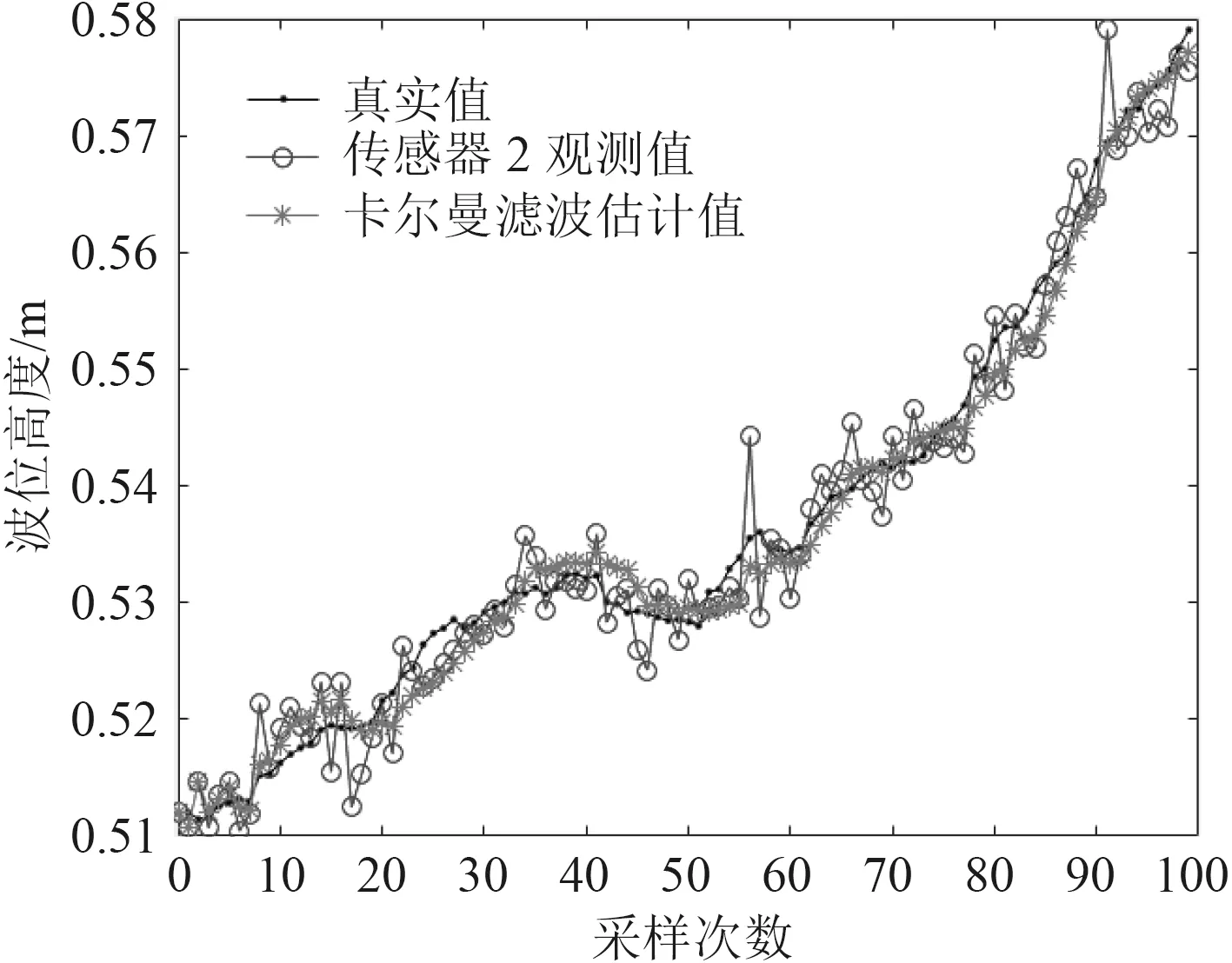
圖9 傳感器2 的測量值與濾波值Fig.9 Sensor 2 measured and filtered values

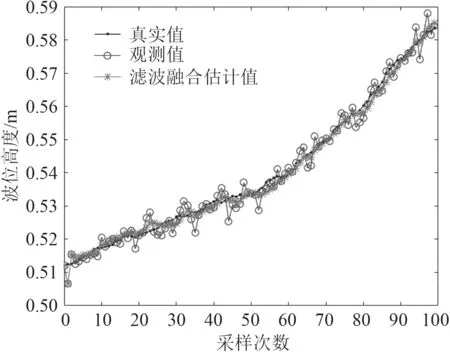
圖10 分布式加權融合卡爾曼濾波Fig.10 Distributed weighted fusion Kalman filtering

由圖10 可見，液位波動的測量值經過最優融合卡爾曼濾波器處理后表示的更加穩定，輸出值趨于真實值，最大波動不超過6 mm，且運行一段時間后輸出基本趨于平穩。因此，可看出濾波融合的效果良好。同時，經過多次測量比較，采用本系統測量的液位值平均誤差在0.5%以內，滿足系統設計要求，可見采用分布式最優加權融合卡爾曼濾波器的濾波效果良好。表1為試驗所用的100 組數據計算的誤差。

由表1 可得，本文實驗中液位監測的方法雖然在測量前對傳感器進行了預處理，可測量后的誤差仍然較大。在單傳感器測量下，采用卡爾曼濾波產生的誤差較小，而多傳感器濾波融合后的誤差最小。由此可見，多傳感器融合算法具有較高的精度。因此，在精度要求高的液位監控系統中可考慮采用本文提出的多傳感器融合方法。

表1 液位測量精度比較Tab.1 Comparison of liquid level measurement accuracy

5 結 語

本文針對船舶液位監測過程中液位測量易出現的誤差，且考慮到單傳感器測量數據容易產生偏差，提出一種在時滯系統下的基于卡爾曼濾波的多傳感器融合算法，給出了多傳感器分布式加權最優融合估計和最優融合誤差。對液位變化過程進行建模，使用此方法對傳感器測得值進行處理，提高液位輸出值的精確度和穩定性。通過仿真和實驗證明，本文采用的對測量數據的處理方法使得到的液位輸出值相比于常用方法更加精確可靠，具有一定的實用性。