基于發射管的UUV 自動回收機械臂動力學研究

楊 釗，景包睿，張 頻

(中國船舶集團有限公司 第705 研究所昆明分部，云南 昆明 650106)

0 引 言

隨著機器人技術的迅猛發展，機器人在軍事領域上的應用越來越廣泛。波音公司為美國海軍研制了以機械臂為主體、基于潛艇魚雷發射管的UUV 回收系統，并于2006 年初完成海試[1]。艦艇通過發射管進行小型UUV 的布放、回收以及物資輸送，具有很強的隱蔽性，應用前景廣闊。目前國內在這方面的研究尚處于空白階段，因此基于發射管的回收機械臂具有較好的實用價值和研究意義。

機械臂裝載在發射管內，因此其體積、外形及重量有著嚴格限制。在機械臂的設計過程中，動力學求解得到的機械臂動態過程中各關節的力與力矩可為驅動校核、優化機械臂結構等工作提供參考。Pratheep V G[2]在Solidworks 中建立了機械臂的三維模型并在Matlab 下進行運動控制仿真。袁凱[3]和鮑俊維[4]分別設計了六功能和五功能的中等負載水下機械臂，并利用牛頓-歐拉法建立了機械臂動力學模型。王懿[5]基于迭代Newton-Euler 矢量力學方法和Morison 方程建立了靜水條件下考慮流體阻力的六自由度機械臂動力學模型，通過Matlab 軟件仿真分析了流體阻力對機械臂關節控制力矩最大影響。

本文針對艦艇的回收打撈需求，對機械臂進行結構設計，建立虛擬樣機模型得到相應的動力學參數；規劃回收軌跡求解機械臂的關節驅動力矩；最后對比分析浮力、負載重量、負載空間尺寸對機械臂的動力學特性的影響。

1 機械臂的結構設計與三維模型

1.1 機械臂的總體結構設計

基于發射管的回收機械臂在待機時能回縮在發射管內，伸展后能完成“抓取-對齊-回收”任務。其中，機械臂待機時的回縮功能可通過改裝機械臂的安裝平臺來實現，但機械臂需要具備折疊功能，并保證折疊后的包絡圓直徑要小于發射管的管徑。總體參數為：折疊后的包絡圓直徑不大于300 mm，最大伸展長度為2 m，負載為10 kg、長度800 mm 的圓柱狀負載。

自由度是衡量機械臂運動靈活性的主要技術指標，同時也衡量著機械臂結構的復雜程度[6]。常見的結構緊湊水下機械臂自由度較少，而自由度較多的水下機械臂結構尺寸較大，美國Schilling Robotics 公司的Orion4R 機械臂（見圖1）和Titan4 機械臂（見圖2）。基于發射管的回收機械臂對靈活性要求較高，需要六自由度來確保能夠以多種姿態抓取不同位置的物體并完成回收。另外，由于旋轉關節相比移動關節靈活性較高、占地空間較小而且工作空間更大，回收機械臂的6 個關節選擇旋轉關節。根據Pieper 法則[7]，機械臂相鄰的3 個關節軸線平行或交于同一點時，機械臂逆運動學有封閉解。因此本文設計的回收機械臂第4、第5 和第6 關節軸線交于一點。此時機械臂的前3 個關節控制末端夾爪的位置；后3 個關節控制末端夾爪的姿態，可視為由定位機構和定向機構組成。

圖1 Orion4R 機械臂Fig.1 Orion4R manipulator

圖2 Titan4 機械臂Fig.2 Titan4 manipulator

為了實現機械臂能夠在發射管內伸縮的功能需求，機械臂采用可折疊方案，以保證機械臂折疊后具有較小的包絡圓直徑及足夠大的臂長。目前主流的折疊結構分為兩折疊式和三折疊式，如圖3 所示。兩折疊式機械臂的結構方案伸展距離有限，多數應用于工業、協作等對于工作范圍要求不大的場合；三折疊型機械臂有更長的臂展，但在同等的包絡圓直徑下臂截面較小，承載能力不高。考慮到回收機械臂空間尺寸的限制和承載能力，回收機械臂采用兩折疊型，連接臂從常見的圓筒形改為便于折疊的單板結構。

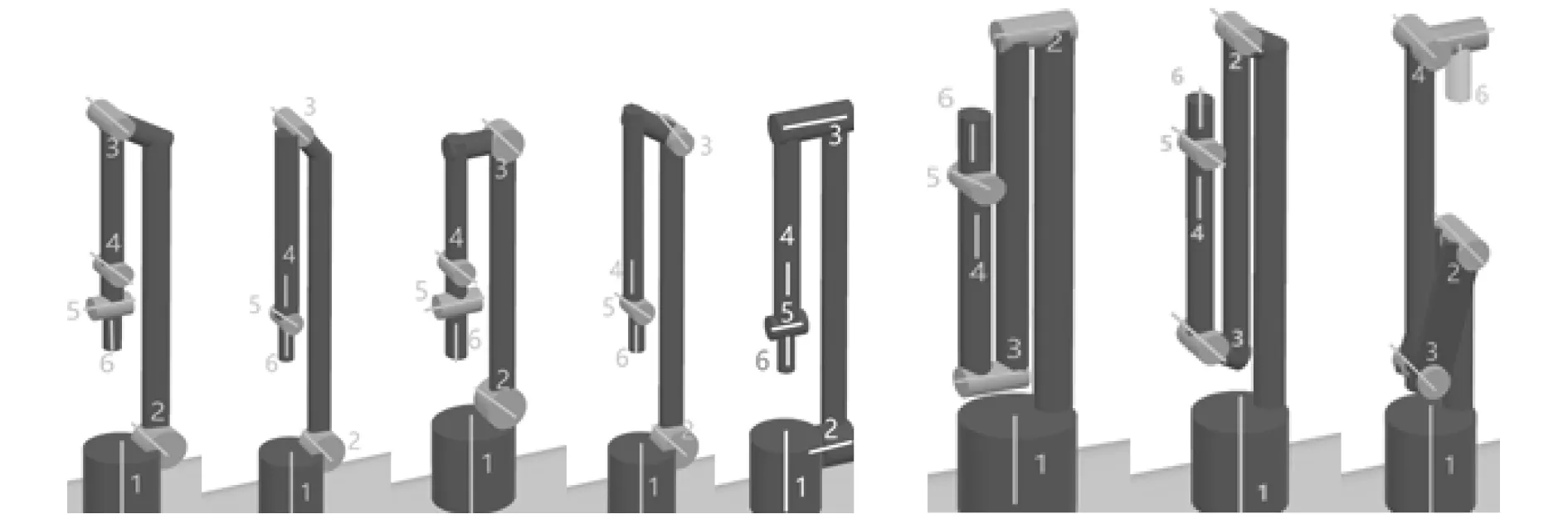
圖3 兩折疊型與三折疊型機械臂Fig.3 Two fold and three fold manipulators

1.2 機械臂的三維模型

通過分配臂長-驅動校核-改進臂長分配的動態優化過程，確定回收機械臂結構簡圖如圖4 所示。選擇合適的電機、材料后用Solidworks 三維設計軟件繪制的三維模型如圖5 所示。

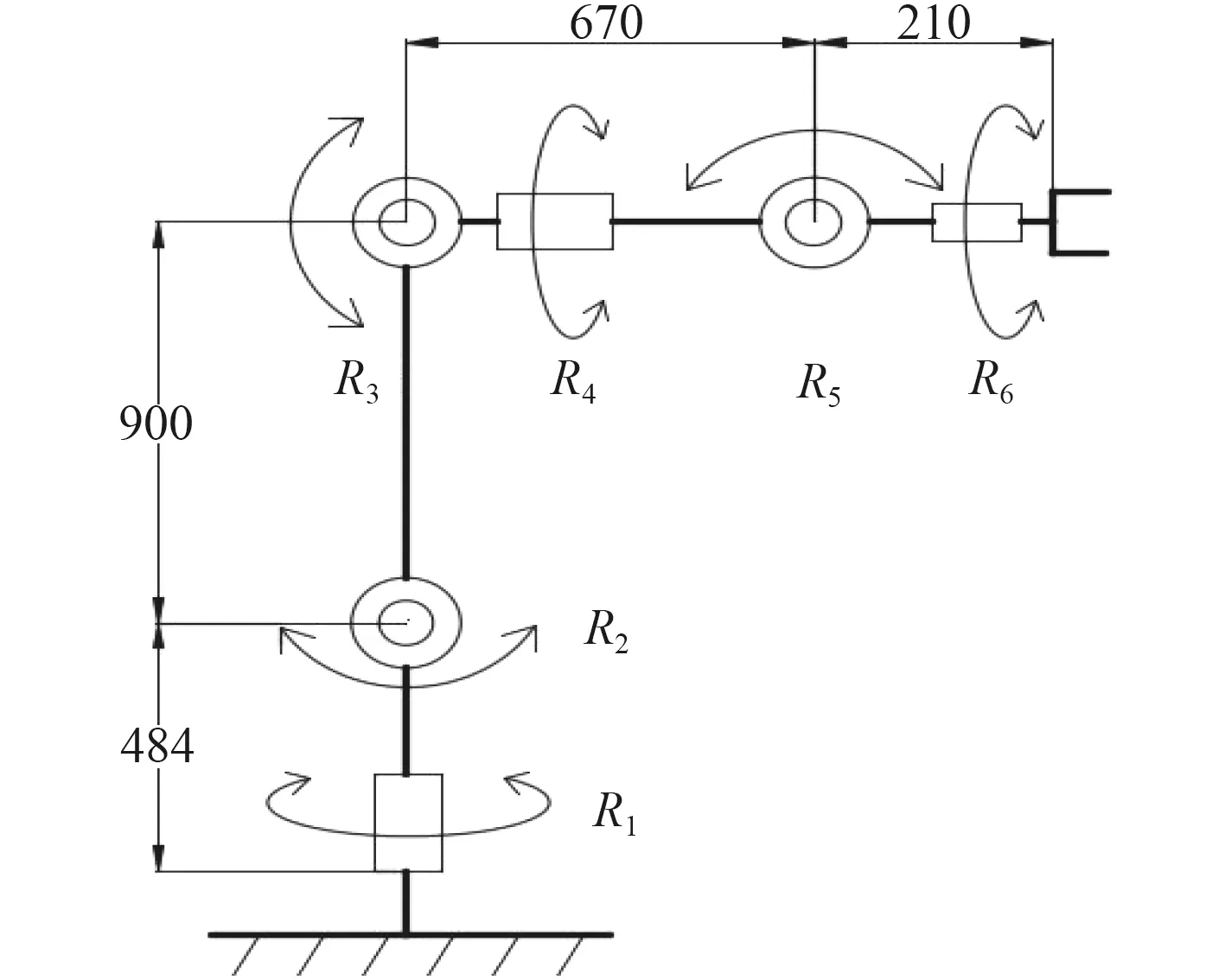
圖4 回收機械臂的結構簡圖Fig.4 Structure diagram of recovery manipulator

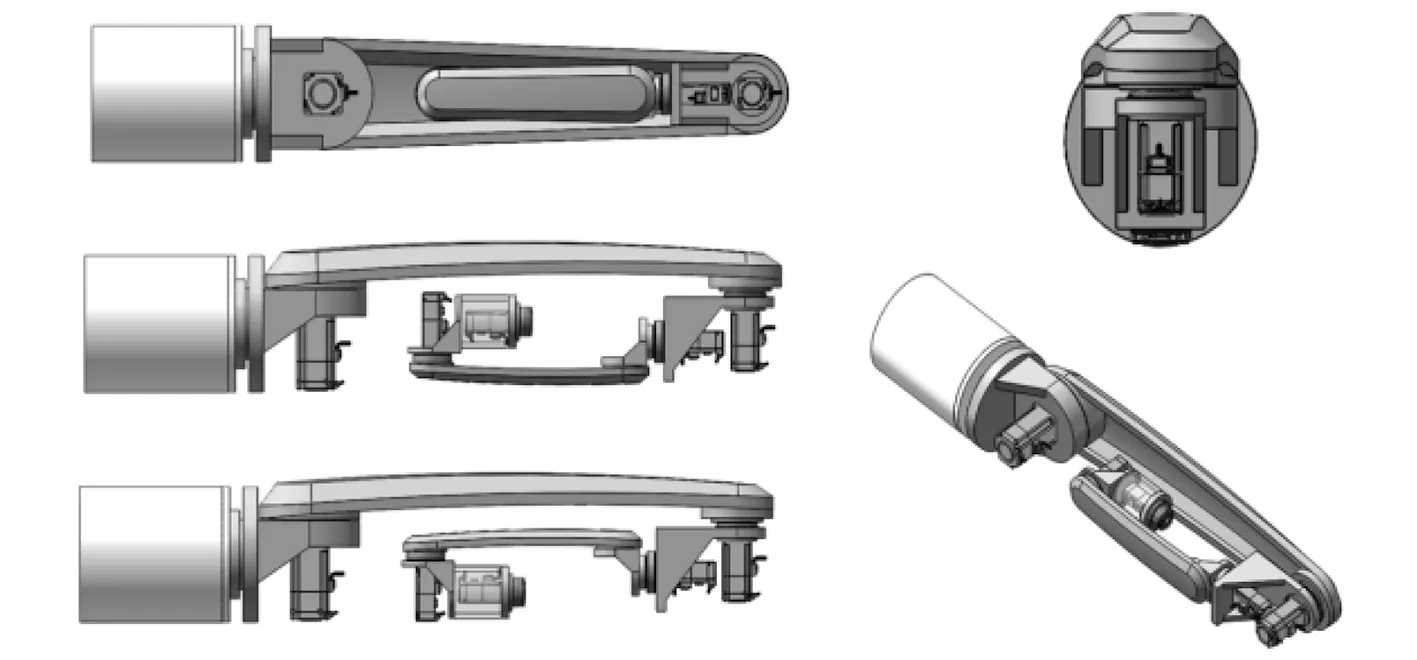
圖5 機械臂的虛擬樣機模型Fig.5 Virtual prototype model of manipulator

建立三維模型后，利用Solidworks 軟件中的質量評估功能[8]獲取機械臂6 個連桿的質量及動力學參數。

質量：46.5 kg，44.9 kg，14.2 kg，5.3 kg，3.5 kg，2.7 kg。

關節坐標系下的連桿質心：

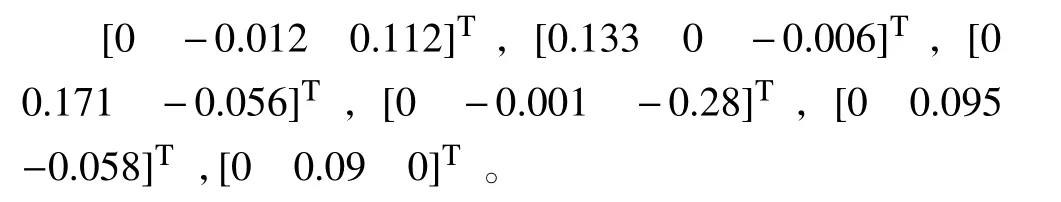
質心坐標系下的慣性張量：

2 機械臂動力學方程的建立

牛頓一歐拉法建立動力學方程原理是在建立連桿間的速度傳遞關系，得到各旋轉關節的角度和角速度后，利用牛頓方程與歐拉方程求解各個連桿的慣性力與慣性力矩（式(1)和式(2)），最后通過連桿質心處的力平衡與力矩平衡方程求解關節的力與力矩。

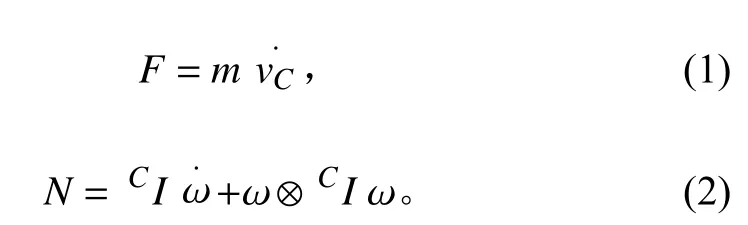
其中：F和N表示連桿質心處的合力與合力矩；CI為連桿在質心坐標系中的慣性張量；為連桿質心加速度，關節的角速度與角加速度。

為求解連桿質心速度與加速度，根據正運動學建立的連桿間的變換關系，從連桿1 到連桿6 向外遞推：

通過連桿質心上的力和力矩平衡方程可得：

最后，在力和力矩平衡方程式(4) 中令i=6 →1，從連桿6 向連桿1 進行力和力矩的迭代計算，即可求出所有驅動關節上的力與力矩。

至此，動力學方程的推導已完成。輸入機械臂連桿質量、動力學參數（質心、慣性張量）和關節的運動軌跡（角度、角速度、角加速度）即可求解關節驅動力矩。

3 機械臂工作過程的動力學仿真

3.1 回收過程軌跡規劃

機械臂的軌跡規劃分為笛卡爾空間規劃與關節空間規劃，規劃的方法有線性、多項式插值和樣條插值等[9]。回收過程屬于常規的點到點運動，可采用關節空間軌跡規劃；多項式軌跡規劃能滿足插值結果連續、平滑的要求，同時回收機械臂起點和終點的速度和加速度及路徑點都可確定，因此采用七次多項式[10]進行插值。

在七次多項式下，關節角、角速度、角加速度設置如下：

七次多項式的工作軌跡有8 個系數，需要8 組方程來確定。在確定回收機械臂起點t0=0 和終點tm時的角度θ、角速度和角加速度后，選取2個中間點t1，t2的關節角即可求解工作軌跡：

回收機械臂的工作過程如圖6 所示。

圖6 機械臂回收過程Fig.6 End pose at intermediate point

根據末端坐標系與基坐標系的關系確定各路徑點的位姿矩陣，并由逆運動學方程轉化關節角，選取關節角最接近的一組解，結果如表1 所示。

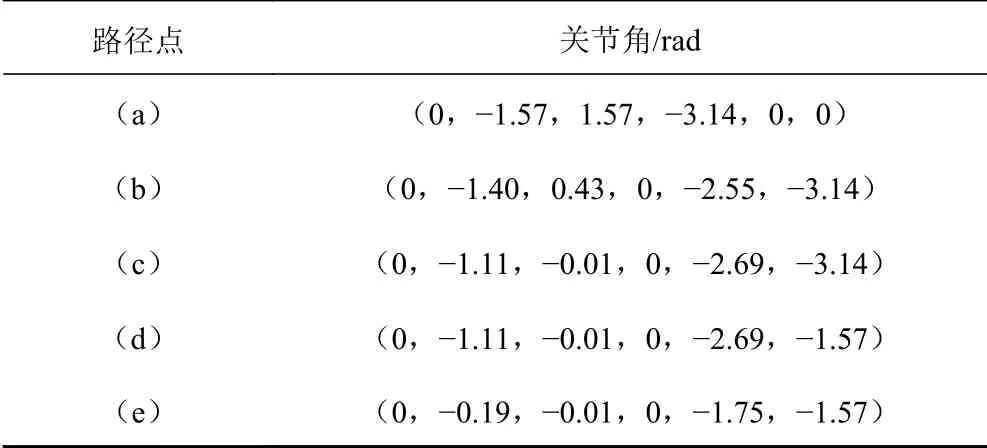
表1 各路徑點關節角Tab.1 Joint angle of each path point

艦艇在回收水面或水下目標時，往往處于超低速或靜止狀態，因此在仿真時不考慮艦艇運動的影響。本次仿真設定目標回收物位于機械臂基坐標系右方1 m、下方1.2 m 處；回收管軸線在基坐標系下方1 m 處，管口與機械臂底座對齊。由于機械臂在回收過程的起點、抓取點及終點處均為靜止狀態，分別對抓取過程（a）～（c）和回收過程（d）～（e）的工作軌跡進行規劃。設定起點和終點角速度、角加速度分別為0 m/s 和0 m/s2，抓取過程和回收過程的運動時間分別為14 s 和16 s，采用七次多項式插值后得到的各關節角度、末端運動軌跡和關節角速度如圖7～圖9 所示。

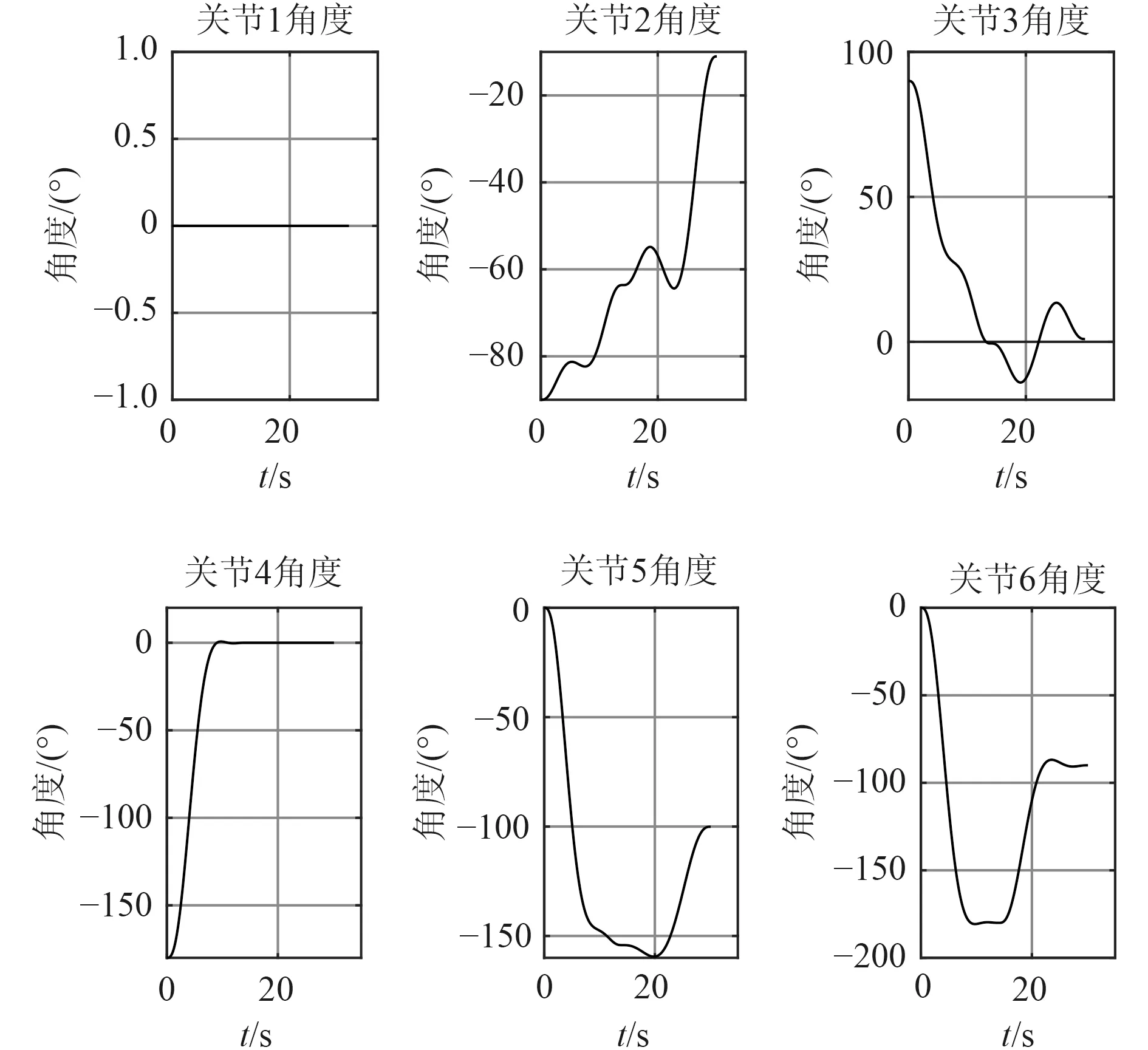
圖7 回收過程中各關節的角度變化曲線Fig.7 The angle curve of each joint

圖8 回收過程中末端運動軌跡Fig.8 The trajectory of the end in the recycling process

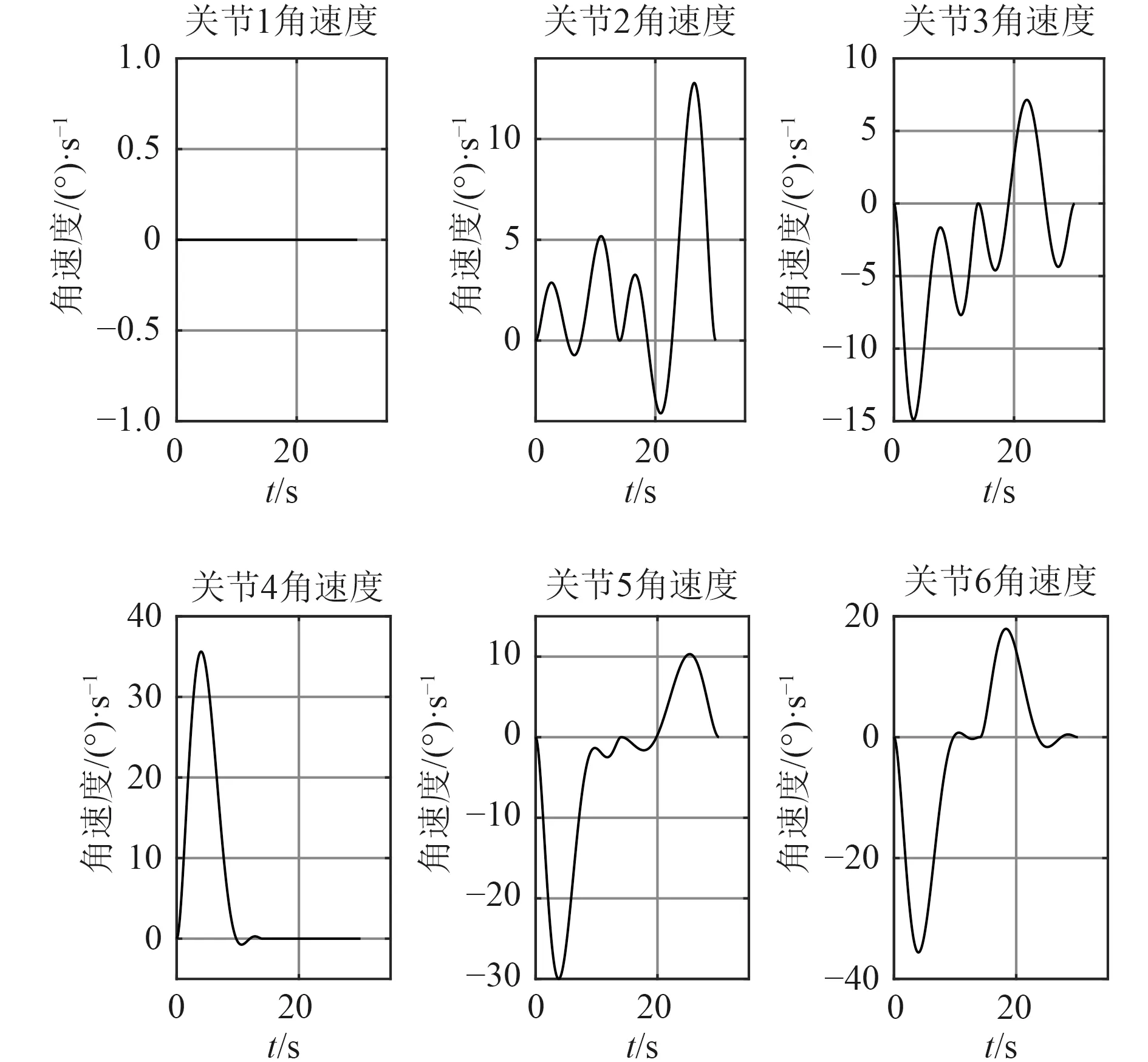
圖9 回收過程中各關節的角速度變化曲線Fig.9 Angular velocity curve of each joint

軌跡規劃的結果顯示，機械臂在0 s 時處于折疊狀態；在0～14 s 期間伸展并運動到目標物處。在14 s時，機械臂的角速度及角加速度都為零，說明機械臂已停穩在目標物處。14～30 s 期間機械臂重新啟動，開始抓取目標物、完成目標物軸線與回收管道軸線對齊并移動到回收點處的任務。機械臂在工作過程中角度的變化曲線平滑無斷點，角速度無突變情況，運動的穩定性基本滿足要求。

3.2 動力學方程的求解

在得到機械臂的運動規律后，結合獲取的動力學參數，通過建立的動力學方程即可求解關節實時力矩。下面分別將浮力、目標負載的重量和空間尺寸作為變量進行動力學仿真，分析其對回收機械臂動力學特性的影響。

在考慮重力因素時，設定回收機械臂基坐標系{0}處的質心加速度g=9.8 m/s2，這等價于機械臂以加速度9.8 m/s2向上做加速運動，這個假想的加速度與重力作用在連桿上的效果相同。另外，在同時考慮重力與浮力因素時，根據回收機械臂與水的密度比，設定基坐標系質心加速度g1=6.6 m/s2，求解結果如圖10 所示。

從圖10 可看出，在考慮浮力時關節所需的驅動力矩較小，這是因為浮力抵消了回收機械臂部分重量，減小了關節處的重力力矩。浮力對關節力矩的影響較大。例如在0 s 時，浮力可減小關節2 約40%驅動力矩。

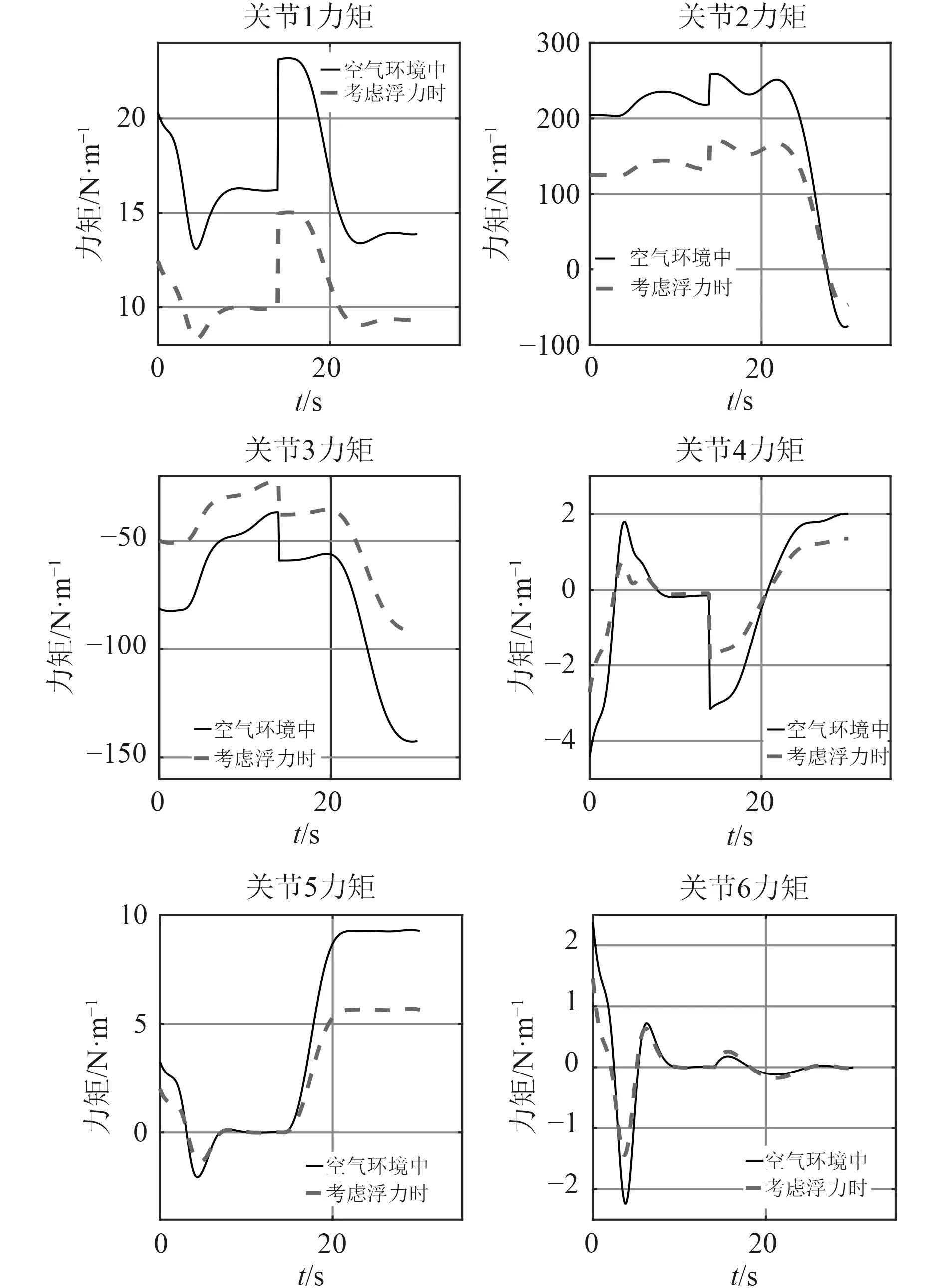
圖10 考慮浮力下的力矩對比曲線Fig.10 Driving torque curve considering buoyancy

此外，分別在5 kg，7 kg，10 kg 的負載重量下按照相同的運動軌跡進行回收機械臂動力學的求解，結果對比如圖11 所示。

圖11 不同負載重量下的力矩對比曲線Fig.11 Driving torque curve considering load

從圖11 可看出，回收機械臂在14 s 時抓取回收物，因此在14 s 前各個重量下的力矩曲線相同。負載的重量與關節所需驅動力矩呈正相關關系，負載重量越大，關節所需驅動力矩越大，負載重量不影響關節力矩曲線的趨勢。

為研究不同尺寸的回收物對驅動力矩的影響，現假設手爪夾在離質心20 cm，此時產生的額外力矩為2 N/m，繞x軸順時針轉動。計算關節力矩時，需在牛頓-歐拉法中“內推”部分末端連桿的力矩平衡中加上額外力矩再進行迭代，得到的關節力矩對比曲線如圖12 所示。

圖12 考慮夾持位置下的力矩對比曲線Fig.12 Driving torque curve considering load size

在14 s 時回收機械臂夾取負載時姿態如圖13 所示，此時額外力矩與關節2、關節3 和關節6 的旋轉平面垂直，關節1 和關節4 的旋轉平面與額外力矩不垂直。因此關節1 和關節4 的力矩曲線在14 s 時的力矩不同，關節2、關節3 和關節6 的力矩曲線在14 s 時相同。

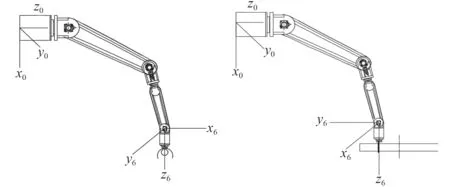
圖13 機械臂在抓取和回收時的姿態Fig.13 manipulator attitude in grasping and retrieving

在14 s 后，回收機械臂夾取負載并進行姿態變換，將負載軸線與回收管的軸線對齊。此時不同夾持位置產生的額外力矩與關節1、關節4 和關節6 的旋轉平面垂直，與關節2、關節3 和關節5 的旋轉平面不垂直。因此夾持位置對于關節1 和關節4 的影響逐漸減小；對關節2、關節3 和關節5 的影響逐漸增大。由于6 號回轉關節與柱狀負載的軸線相垂直，因此夾持位置對6 號回轉關節的驅動力矩無影響。

4 結 語

本文建立了基于發射管的回收機械臂三維模型，完成了回收軌跡規劃與動力學仿真。軌跡規劃結果表明回收機械臂能靈活完成打撈回收的動作；動力學仿真結果表明回收機械臂能抓取回收規定的負載，且浮力、負載的重量和空間尺寸均對關節驅動力矩有一定影響，在進行動力學分析時不可忽視。

本文進行的動力學仿真為后續驅動校核與控制系統設計等工作提供一定的參考。研究中，回收機械臂在水中運動時水動力僅考慮了浮力因素，且動力學參數由三維模型設計軟件計算得到，沒有考慮關節摩擦和彈性以及實際加工裝配誤差等因素，因此仿真結果與真實應用情況存在一定差異。下一步需要進行動力學參數辨識，并加入水阻力、附加質量力等因素，提高動力學仿真的精度。