HyTRV流場特征與邊界層穩定性特征分析

陳堅強，涂國華，萬兵兵,*，袁先旭，楊強，莊宇，向星皓

1. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室， 綿陽 621000

2. 中國空氣動力研究與發展中心 計算空氣動力研究所， 綿陽 621000

3. 中國空氣動力研究與發展中心 超高速空氣動力研究所，綿陽 621000

自20世紀50年代起，高超聲速飛行器已成為各航空航天大國的重點關注對象。高超聲速飛行器飛行時有失敗，比如美國X-15擋風罩破碎和燃料箱支架燒壞、哥倫比亞航天飛機失事、HTV-2飛行試驗失敗等。為了發展先進的高超聲速飛行器，美國在20世紀80年代啟動了國家空天飛機(National Aero-Space Plane，NASP)計劃，但因缺乏科學的理論指導最終沒能成功，不得不轉向對簡單模型的基礎研究，高超聲速邊界層轉捩問題是其中亟需解決的關鍵問題之一[1]。由于邊界層的層流和湍流兩個流動狀態對飛行器摩擦阻力、噪聲、表面熱流等方面存在著巨大差異，對飛行器的安全和氣動性能具有顯著的影響[2-4]。因此，研究高超聲速邊界層轉捩問題，預測層流到湍流的轉捩位置，對飛行器的氣動設計和熱防護設計尤為重要。

一般來說，邊界層轉捩是由邊界層模態失穩導致的，其失穩機制研究已近百年。失穩模態主要包括第一(T-S波)/第二模態、橫流失穩模態、流向渦失穩模態、G?rtler失穩模態和附著線失穩模態等。對于不同模型，觸發轉捩的主導模態可能會不一樣。第一(T-S波)/第二模態之于無后掠無攻角的平板和錐形等[5-10]；橫流失穩模態之于有后掠或有攻角的平板、錐形、機翼等[11-15]；流向渦失穩模態之于一般曲面模型等[16-17]；G?rtler失穩模態之于流向負曲率(凹面)區域[18-20]；附著線不穩定模態之于后掠翼拋物化前緣等[21-22]。對于一些特定復雜模型，轉捩甚至可能是通過多種失穩模態相互作用完成的。

長期以來，轉捩機理研究一般基于平板、槽道、圓錐等簡單外形開展，雖然取得了大量的研究進展，但例如模態干擾/轉換、攻角效應、鈍度效應等的認知還存在不足甚至相互矛盾之處，對復雜飛行器的轉捩預測與控制能力不足，飛行器相關設計(如熱防護系統設計)時不得不采用較大的設計余量。目前，國內外已經開始重視轉捩機理研究與真實飛行之間的匹配，飛行試驗也越來越多地參與其中，比如美國近十多年來從HIFiRE-1的圓錐發展到HIFiRE-5的橢圓錐[23]，再發展到近兩年的多曲面體邊界層轉捩(Boundary Layer Transition，BLT)[24]，所涉及的流動和轉捩機理也越來越復雜。中國空氣動力研究與發展中心(CARDC)成功完成了高超聲速轉捩研究的MF-1 飛行試驗[25-27]，該試驗主要研究圓錐邊界層第二模態失穩導致的轉捩問題。

縱觀國內外，目前所用的高超聲速轉捩研究標模仍然存在不足。不論是HIFiRE-1和MF-1的圓錐外形，還是HIFiRE-5的橢圓錐，甚至是BLT的四象限曲面外形，都與真實高超聲速飛行器有較大差異，且有的外形不是全解析光滑外形，比如HIFiRE-5外形的頭部與錐身的過渡段不是解析的，需要采用數模定義，不利于研究人員相互交流。

為進一步研究三維復雜外形的高超聲速飛行器邊界層轉捩問題，CARDC提出并設計了一款更接近真實飛行器典型氣動布局特征、全數學解析光滑的升力體模型，名為高超聲速轉捩研究飛行器(Hypersonic Transition Research Vehicle，HyTRV)。本文針對HyTRV模型，主要利用高精度數值模擬方法分析基本流特性，利用線性穩定性理論(LST)和eN方法分析穩定性特性，為開展更多更細致的數值模擬、理論分析、風洞試驗和飛行試驗研究給出參考建議。

1 HyTRV外形與計算參數

1.1 HyTRV外形

HyTRV外形為全數學解析光滑的升力體外形，如圖1所示。頭部區域為長短軸比2:1的橢球型，下表面逐漸光滑過渡到長短軸比4∶1的橢圓型，上表面設計成由CST函數與橢圓函數共同控制的“幾”字形狀。為了表述方便，上表面的最高點稱為模型的頂端，上表面兩側向內彎曲的地方稱為腰部，下表面的最低點為橢圓型的短軸端，最低點連線稱為下表面中心線。在上表面與下表面之間的連接區域對應于橢圓型的長軸端，其位置類似于后掠前緣，稱為前緣附著線(簡稱附著線)。

圖1 HyTRV外形

1.2 計算參數

本文選擇風洞試驗工況作為計算工況，以便后續風洞試驗研究參考，參數見表1。其中，Ma∞代表來流馬赫數，Re代表單位雷諾數，α′代表攻角，向上為正，p0代表總壓，T0代表總溫，T∞代表來流溫度，Tw代表壁面溫度。

表1 計算工況

2 數值計算與穩定性分析方法

2.1 數值模擬方法

針對HyTRV模型，本文以貼體曲線坐標系下的三維守恒型Navier-Stokes方程為流動控制方程。

由于邊界層穩定性分析對基本流場的精細度要求較高，因此采用高精度數值格式。無黏項采用五階精度的加權緊致非線性格式(WCNS)[28-29]；黏性項采用五階精度的半節點/節點交錯格式[30]，邊界上采用三階精度單側差分格式；時間項采用隱式LU-SGS方法[31]，并采用SFD (Selective Frequency Damping)方法[32]提高計算收斂能力。壁面采用無滑移、等溫條件；遠場給定自由來流；出口為線性外推。

2.2 穩定性分析方法

根據線性穩定性理論，小幅值擾動可寫成行進波形式：

(1)

eN方法是基于LST的一種轉捩預測方法，基本理念是邊界層內各種頻率和空間波數的擾動波進入不穩定區域后，其幅值將被放大，放大倍數可表示為eN；對于不同頻率和空間波數的擾動波，其開始失穩的位置和增長率通常不相同；所有擾動波幅值放大倍數的N值曲線構成包絡線，即為整個邊界層擾動演化的幅值曲線。可通過包絡線N值大小來判斷轉捩是否發生。對于二維轉捩問題，擾動幅值沿流向ξ方向放大，其N值可表示為

(2)

式中：ξ0是擾動波剛進入中性區域的流向位置。對于一般三維問題，還需要考慮周向變化，因此式(2)還需要考慮周向波數及增長率以及沿三維空間方向的積分路徑。然而周向波數沿空間方向一直變化，勢必增加迭代求解難度。本文采用天津大學羅紀生團隊發展的局部區域等效展向波數法[34]確定擾動波的周向波數和積分方向。三維問題的eN求解方法和軟件開發思路具體見文獻[35]。

2.3 網格無關性驗證

為驗證網格無關性，流場計算和穩定性分析測試了3套網格，半個模型(不計頭部)流向×法向×周向的網格數分別grid1：1 310萬(211×201×309)，grid2：2 354萬(211×361×309)，grid3：4 901萬(301×361×451)。圖2在3套網格下比較了工況1(表1)的基本流，可見基本流等值線基本完全重合(圖2(a))，速度剖面也基本完全重合(圖2(b))，表明這3套網格的網格密度在計算基本流方面已經足夠。圖中：η表示垂直壁面方向上的坐標，L為升力體總長度。圖3給出了3套網格下的N值對比結果，可見在大部分區域的N值等值線也基本完全重合，僅在中心線附近有所差別。造成這種差別的原因是該區域的基本流高度三維化，不穩定模態對基本流的變化更為敏感，穩定性分析對基本流要求更高。由此說明這3套網格在除流向渦區域外的其他區域中流向、法向和周向均滿足網格無關性。本文選用grid2，即211×361×309的網格進行更詳細的分析。

圖2 不同網格下x/L=0.625處橫截面流向速度云圖與不同周向位置的流向速度剖面

圖3 不同網格對應的N值云圖(下表面)

3 HyTRV流場

3.1 流向渦

針對表1中工況1～6，利用高精度數值模擬獲得HyTRV基本流場。圖4和圖5分別給出不同攻角下的壓力p云圖和流向速度云圖,4個截面位置為x/L=0.106 3,0.312 5,0.625 0,0.937 5。圖中：HPZ指高壓區，LPZ指低區。圖6給出工況1近壁區的流線分布。由圖4(a)可以看出，根據模型的外形特征，模型的附著線和頂端附近的激波強度比下表面中心線和腰部強，前兩者激波后的壓力比后兩者高，因此橫截面上存在周向壓力梯度。為平衡周向壓力梯度，流動從高壓區(附著線和頂部)向低壓區(下表面中心線附近和腰部)匯聚(圖6)，匯集到一定程度后形成流向渦結構，如圖5(a)所示。當攻角增加時，下表面中心線附近壓力增大，導致下表面流向渦結構變扁；上表面頂端壓力減小，低壓區逐漸由腰部向頂端移動，導致腰部流向渦結構逐漸移向頂端(圖5(b))。攻角為4°時，上表面靠近附著線的區域又出現一種低壓區(圖4(c))，對應多出一個流向渦結構(圖5(c))。攻角為6°時，上表面頂端區域成為低壓區(圖4(d))，對應形成流向渦結構(圖5(d))。繼續增加攻角，下表面中心線附近壓力繼續增大，以致下表面的周向壓力梯度逐漸消失(圖4(f))，因而流向渦結構繼續扁平而最終消失(圖5(f))；上表面兩個低壓區進一步擴大和增強，導致上表面中心線附近出現流向渦，腰部的流向渦也逐漸向上表面中心線靠近，多個流向渦相互干擾，渦結構變得更加復雜(圖5(e)和圖5(f))。

圖4 不同攻角下的壓力云圖

圖5 不同攻角下的流向速度云圖

圖6 0°攻角流場在中心線附近和腰部區域流線匯聚(工況1)

基于流向渦隨攻角的變化情況，建議從如下3個方面研究HyTRV模型的流向渦失穩：

1) 針對小攻角工況研究下表面中心線的流向渦失穩及轉捩機理。此流向渦的形成機制與HIFiRE-5橢圓錐模型短軸處流向渦形成機制相同，流向渦都呈現蘑菇狀分布。

2) 針對大攻角工況研究上表面多個流向渦干擾及轉捩機理，可用來表征真實高超聲速飛行器大攻角飛行時的背風面轉捩情況。

3) 針對攻角變化情況研究不同扁平程度的流向渦失穩及轉捩機理。

流向渦產生之前，通常要經歷橫流階段，橫流失穩與流向渦失穩相互干擾，可能會出現更多的渦/波結構。下文將對HyTRV的橫流特征進行分析。

3.2 橫 流

在流線匯聚之前，邊界層內存在由高壓區到低壓區的橫向流動，其速度從壁面到邊界層外緣為從零迅速增加然后迅速減小直至邊界層外緣附近時再緩慢減小接近于零，該橫向流動稱為橫流。邊界層外的流動受周向壓力梯度影響很小，基本沿無黏勢流向方向，因此在橫流區域中邊界層外的勢流流線與邊界層內黏性流線之間存在較大的夾角。圖7給出了表1工況1的模型下表面和側面的勢流流線與壁面黏性流線的分布。根據這種特性，圖中可以判斷出在0°攻角下橫流主要分布在附著線與中心線之間、腰部與附著線之間、頂端與腰部之間的3個區域，分別記為Zone 2、Zone 3、Zone 6。

圖7 0°攻角的勢流流線和近壁面流線分布(工況1)

橫流雷諾數Recf常用來判斷流場中橫流區域分布及其強度。橫流雷諾數越大，說明橫流效應越強。計算形式為

(3)

圖8和圖9分別給出不同攻角上下表面的橫流雷諾數云圖。可以看出，除去腰部和下表面中心線附近的流向渦區域，當攻角為0°時，有3個區域的橫流雷諾數較大，分別對應Zone 2、Zone 3和Zone 6。說明這3個區域的橫流效應比較強，且下表面Zone 2更強。隨著攻角的增加，下表面Zone 2的橫流雷諾數逐漸減小，上表面Zone 6也減小，但Zone 3卻逐漸增大。這是因為攻角增加時下表面周向壓力梯度逐漸減小，橫流效應逐漸減弱；而上表面低壓區從腰部逐漸移到頂端，使Zone 6區域變窄，Zone 3區域變寬，同時頂端壓力逐漸減小，使Zone 6壓力梯度逐漸減小，從而Zone 6橫流效應減弱，而Zone 3橫流效應增強。

基于橫流強度隨攻角的變化情況，建議從如下3個方面研究HyTRV模型的橫流失穩：

1) 針對0°攻角工況研究3個相對獨立區域的橫流失穩及轉捩機理。這3個相對獨立的橫流區域為下表面的Zone 2和上表面的Zone 3和Zone 6，且以Zone 2的橫流最強，分布區域最大。

2) 針對不同攻角工況研究不同橫流強度的失穩及轉捩機理。此時下表面的Zone 2區域是比較理想的研究區域，橫流強度隨著攻角增加而逐漸減弱(圖8)。

圖8 不同攻角下表面的橫流雷諾數分布

3) 針對中等和大攻角(比如6°～10°攻角)研究上表面Zone 3區域的橫流失穩及轉捩機理(圖9)。此時Zone 3區域類似于高超聲速飛行器“機翼”背風面的橫流區域。

圖9 不同攻角上表面的橫流雷諾數分布

4) 針對HyTRV模型腰部區域，應對橫流失穩與流向渦失穩的相互干擾做詳細研究。因為橫流區域與流向渦區域交替出現，橫流不穩定性的參與，會引入更多的渦/波結構。

4 穩定性與eN分析

對第3節提到的流場區域，除了LST失效的流向渦區域外，其他區域都可采用LST進行穩定性分析，從而求解出該區域的不穩定模態N值分布。下表面中心線附近和腰部(或者更多部位)的流向渦結構是一個法向和周向變化的二維結構，LST分析失效，但可采用二維全局穩定性(BiGlobal)或求解三維拋物化穩定性方程(PSE3D)的分析方法，本文暫不研究。

分析表明所有的第一模態都是穩定的，這可能是由于馬赫數較高、壁溫較低，故不展示第一模態的分析結果。附著線位置的流場特征類似于圓錐表面的母線，其附著線不穩定性也是邊界層的一種失穩機制，穩定性分析需要考慮。下文主要從橫流失穩模態、第二模態、前緣附著線失穩模態討論HyTRV的邊界層穩定性特征。

4.1 橫流失穩模態

圖10和圖11給出表1工況1的橫流模態不同頻率下的N值分布，頻率范圍為0～40 kHz，圖中分別給出上下表面的結果。可以看出在第3節提到的3個區域中均存在對應的橫流不穩定模態，如圖10(a)和圖11(a)所示，其中下表面Zone 2中的模態最不穩定。增加模態頻率對比分析發現，Zone 6中0 kHz頻率的定常橫流模態相比其他頻率最不穩定。但并不是所有橫流模態都是這樣的，Zone 2和Zone 3中最不穩定頻率大概在20 kHz(見圖10(b)和圖11(c))，N值最高可達15。需要注意的是，圖10(b)和圖11(c)的下表面中心線附近和圖10(b)和圖11(c)中的腰部附近的狹長不穩定區域位于流向渦范圍，失穩特征需要專門研究，此處不討論。

圖10 工況1下表面橫流模態不同頻率下的N值分布

圖11 工況1上表面橫流模態不同頻率下的N值分布

圖12和圖13分別給出表1工況1、2、4、6、7上下表面的橫流模態N值分布，N值包絡的頻率范圍是0～30 kHz。可以看出，在0°攻角時，最不穩定的橫流模態分布在下表面Zone 2。隨著攻角增加，下表面Zone 2橫流模態N值減小，上表面N值增加。當攻角為2°時，上表面N值已經超過下表面。同時注意到，當攻角增加時，Zone 6中的橫流模態逐漸消失，而Zone 3中橫流模態區域不斷擴大，N值不斷增加。直到攻角為10°時，由于上表面存在復雜多變的流向渦結構，求解出的橫流模態N值覆蓋在整個上表面區域。圖12(e)和圖13(e)顯示，增加單位雷諾數，Zone 2、Zone 3和Zone 6這3個橫流區域的N值均顯著增加。

圖12 工況1、2、4、6、7下表面橫流模態的N值分布

圖13 工況1、2、4、6、7上表面橫流模態的N值分布

建議風洞試驗或飛行試驗時參考不同攻角不同區域的橫流失穩特征進行傳感器選型與測點布置。

4.2 第二模態

圖14和圖15分別給出表1工況1、2、4、6、7上下表面的第二模態N值分布，N值包絡的頻率范圍是100～3 000 kHz。可以看出，在前面提到的3個區域中不僅存在橫流不穩定模態，也存在第二模態。而且隨著攻角增加，Zone 2和Zone 6中第二模態逐漸消失，Zone 3中先是增大，約2°攻角時N值開始減小。對比橫流不穩定模態，第二模態的N值略小，因此這3個區域很可能是以橫流模態為主導轉捩。圖14(e)和圖15(e)顯示，增加單位雷諾數(對比圖14(a)和圖15(a))，這3個區域第二模態的N值也顯著增加，但仍小于橫流模態。另外可以觀察到，在附著線附近，N值非常大，遠大于橫流模態，具體分析見4.3節。

圖14 工況1、2、4、6、7下表面第二模態的N值分布

圖15 工況1、2、4、6、7上表面第二模態的N值分布

由于大部分橫流區域也存在第二模態，且在某些工況(比如0°和2°攻角)條件下N值接近橫流失穩模態的N值，所以建議加大第二模態與橫流模態的干擾/競爭、甚至非線性相互作用等方面的研究。第二模態擾動波的頻率基本在100 kHz以上，頻率較高，試驗測量時需要留意。

4.3 附著線失穩模態

圖16 附著線對應的中性曲線

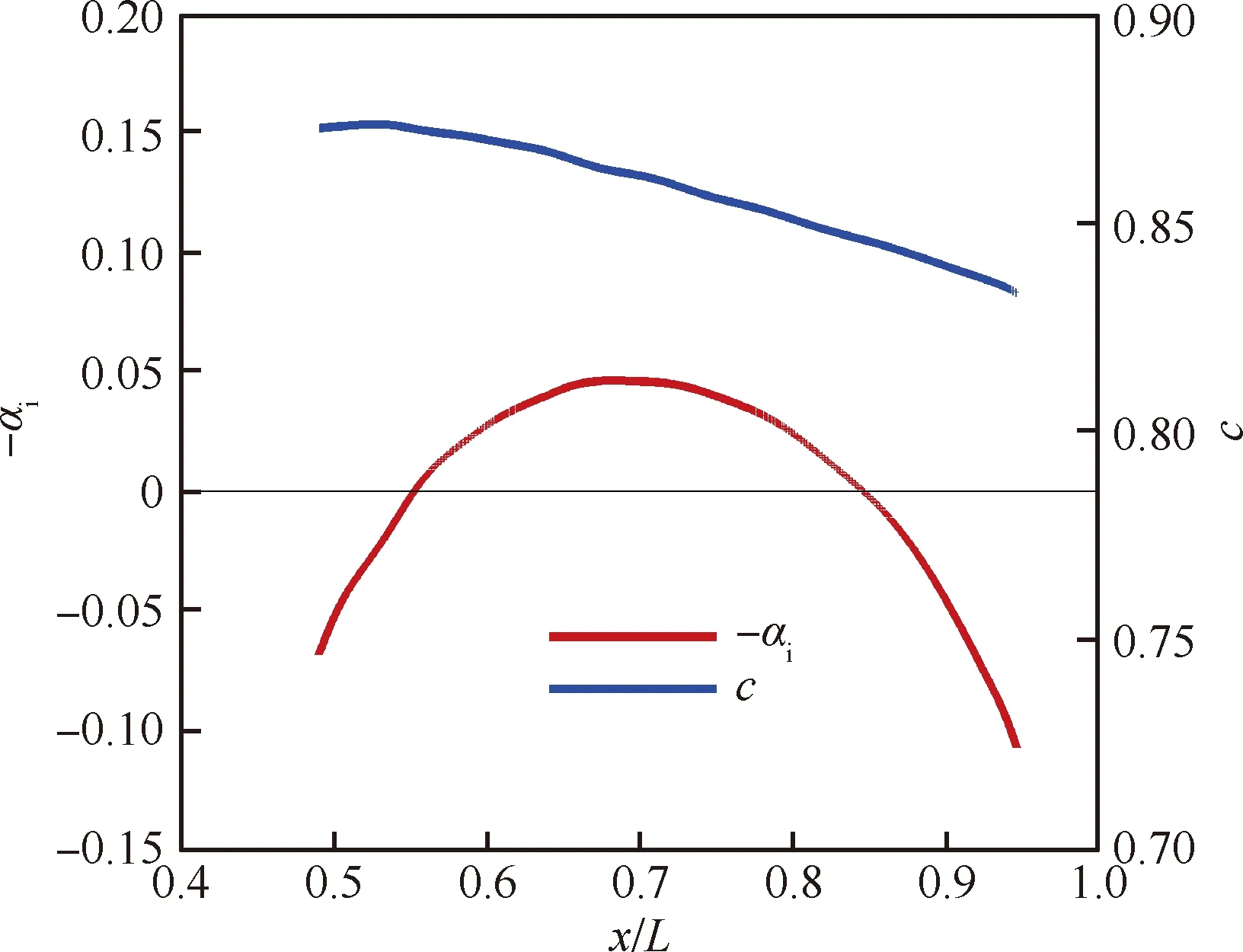
圖17 800 kHz附著線不穩定模態對應的增長率和相速度

圖18 800 kHz附著線不穩定模態的流向速度特征函數

在附著線處，每個頻率從中性曲線下支界開始對增長率進行積分得到N值包絡線，如圖19所示。圖19(a)顯示，N值在x/L=0.94處達到20.3，對應頻率約為755 kHz。改變攻角和單位雷諾數時，x/L=0.94處的N值及頻率均發生變化，如圖19所示，結果見表2。可以看出，當攻角為2°時，N值和頻率均微弱增加；繼續增加攻角，N值和頻率均逐漸減小，而且臨界位置逐漸靠近下游。另外，增加單位雷諾數，N值和對應頻率均明顯增加(見圖19(g))。

表2 x/L=0.94處N值及對應頻率

建議后續通過風洞試驗進一步驗證附著線失穩模態的物理本質，同時需要特別留意附著線失穩擾動波的頻率非常高，在有的工況下甚至超過1 000 kHz (圖19(g))，這已經超過大部分傳感器的響應頻率，比如國內外采用的高頻PCB壓力傳感器的響應頻率也僅為1 000 kHz的量級。

圖19 工況1～7第二模態的N值分布

4.4 eN分析與試驗對比

針對HyTRV模型，CARDC在?2 m激波風洞中進行了初步的風洞試驗驗證，本文僅取表1工況1，模型是上述的1/2縮比模型。風洞試驗中采用溫敏漆獲取轉捩陣面，然后與eN分析結果進行對比分析。在eN分析中，N值包絡的頻率范圍選為0～3 000 kHz，囊括了橫流模態、第一模態(雖然是穩定的)、第二模態以及附著線不穩定模態。N值顯示的是當地最不穩定的模態。如前面所述，Zone 2、Zone 3和Zone 6以橫流不穩定模態為主，附著線附近區域可能是以第二模態為主。針對模型的下表面，圖20給出eN分析與風洞試驗的對比結果，下游深紅色區域表示試驗模型表面的溫度較高，為湍流區，黑色曲線表示eN分析得到的N值等值線，Lt為風洞模型長度。可以看出，風洞試驗中Zone 2區域發生了轉捩，轉捩位置從x/Lt≈0.75的地方開始，對應N值約為5.6，對應頻率在10～40 kHz之間，說明Zone 2發生轉捩是由非定常橫流失穩模態引起的。另外，附著線附近的表面溫度較高，其原因既可能是邊界層轉捩引起的，也可能是附著線前緣的脫體激波引起的。但是因為風洞試驗測量窗口限制及流場視角問題，本次試驗還無法判斷附著線轉捩位置。中心線附近約在x/Lt≈0.56位置溫升梯度開始增大，可能是流向渦失穩引起的轉捩，需要進一步分析。

圖20 eN分析與風洞試驗對比

5 結 論

高超聲速轉捩研究飛行器(HyTRV)是為研究高超聲速邊界層轉捩問題而設計的一款具備真實飛行器典型氣動布局特征的升力體標模。本文利用高精度數值模擬、LST和eN方法分析了該標模的流場特征和邊界層穩定性特征，并與風洞試驗進行了初步對比，得到如下結論：

1) HyTRV模型存在橫流失穩、第二模態失穩、附著線失穩以及流向渦失穩，實現了模型設計目標，即適合多種典型高超聲速邊界層轉捩機理研究。

2) 小攻角情況下，模型表面存在3個相對獨立的橫流區域，橫流區域存在橫流失穩模態和第二模態；針對下表面的橫流區域，eN分析與試驗結果對比顯示，0°攻角情況下導致轉捩的主要機制是橫流失穩。

3) 隨著攻角增加，橫流失穩模態、第二模態、附著線失穩模態的N值均是先微弱增加后逐漸減小，第二模態的減小幅度更加明顯。

4) 增加單位雷諾數，N值顯著增加，即邊界層失穩更明顯，更容易轉捩。

5) 附著線失穩模態的特性與第二模態特性非常一致。

6) 流向渦形成于周向低壓區，出現在下表面中心線附近和腰部區域。隨著攻角的增加，下表面中心線附近的流向渦逐漸消失，上表面腰部的流向渦移向頂端，上表面還同時出現更多的低壓區而形成新的流向渦結構。LST對流向渦分析失效，建議采用BiGlobal和PSE3D進行分析。

本文僅考察了HyTRV標模的主要流場特征和邊界層線性失穩特征，并基于此對后續研究提出了一些建議，這些建議對理論分析、數值模擬、風洞試驗和飛行試驗都較有普適性。

致 謝

本文使用的eN分析方法得到了天津大學黃章峰等同志的幫助，在HyTRV標模設計中得到了中國航天科技集團一院余平和段毅、十一院劉志勇等同志幫助，在這里表示感謝。感謝CARDC超高速空氣動力研究所提供的試驗數據。