飽和橡膠顆粒砂混合料的動力學特性

莊海洋， 劉啟菲， 吳 琪， 李曉雪， 陳國興

(1.南京工業大學 巖土工程研究所, 江蘇 南京 210009; 2.華東交通大學 土木建筑學院, 江西 南昌 330013)

隨著經濟的發展，汽車輪胎的磨耗及汽車的更新換代迅速增加，廢舊輪胎累積量越來越大.由于其難分解且易燃，如果處理不當則會造成環境污染.將廢舊輪胎研磨粉碎后與砂混合而成的橡膠顆粒土，不僅具有密度輕、恢復變形能力顯著、耗能大等特點[1]，而且可以作為輕質替代材料應用于路基、擋土墻的回填，以及橋頭碼頭的隔振等[2-3].砂土液化特性研究多數偏重于常規類型土，對飽和橡膠顆粒土的液化特性研究較少.

要想清晰地了解土體液化破壞過程，自然離不開土工試驗[4-6].Seed等[7]在研究液化問題時大量使用了動三軸試驗數據.Edincliler等[8]、Anbazhagan等[9]亦利用室內試驗探究了橡膠顆粒土的動力特性.Nakhaei等[10]對飽和橡膠顆粒土混合物進行了一系列固結不排水動三軸試驗，提出了能預測不同橡膠摻量下混合物在不同圍壓和小剪切應變幅值條件下的動態特性模型.Senetakis等[11]、Anastasiadis等[12]通過室內試驗研究了不同橡膠摻量下橡膠顆粒土的動力特性.李博等[13]借助循環三軸試驗儀分析了橡膠粉末摻量和橡膠粉末粒徑對橡膠土抗液化強度的影響.Panjamani等[14]探討了橡膠顆粒土的抗剪強度、耗能特性和剛度的變化規律，發現其主要受橡膠粒徑、含量、正應力和圍壓的影響.吳延輝等[15]論證了砂與橡膠顆粒符合隔震裝置的需求.陳輝[16]借助直剪試驗和動三軸試驗探討了橡膠顆粒土抗剪強度的變化規律及影響因素.熊偉等[17]通過振動臺試驗探究了橡膠砂隔振系統的相關性能，發現橡膠砂隔振系統能夠很好地減小上部結構加速度響應.

已有研究多涉及飽和砂土的液化特性，而對飽和橡膠顆粒土的液化特性的系統研究相對不足.鑒于此，本文利用動三軸試驗儀系統探究飽和橡膠顆粒-砂混合料在循環荷載下的動力學響應，結合混合料液化時所表現出來的力學特征，選取應變作為液化判別標準，并從液化強度、剪切應變、滯回圈和能量耗散等角度，考察不同橡膠摻量、不同相對密實度以及不同粒徑條件下橡膠顆粒-砂混合料的液化特性，旨在為橡膠顆粒-砂混合料的相關工程應用提供科學依據和合理的參數.

1 試驗原理和設備

采用GDS動三軸試驗系統進行不排水循環三軸試驗.圍壓和反壓的加載和測量由標準的壓力/體積控制器完成，壓強最大可達1MPa.可獨立控制軸向力，進行靜/動態加載，可施加最大10kN、頻率為2Hz的動態荷載.軸向力傳感器位于試樣頂部，軸向位移傳感器位于試樣底部，在試樣底部施加反壓，在試樣頂部測量超靜孔隙水壓力(Δu).

2 試驗方案

2.1 試驗材料

選用廢舊輪胎粉碎而成的橡膠顆粒與福建砂混合獲得橡膠顆粒-砂混合料，橡膠粒徑(dR)取1～2mm、2～3mm、3～4mm以及4～6mm，砂粒徑為0.075～0.25mm.圖1為橡膠顆粒與福建砂的級配曲線.將各粒徑橡膠顆粒與福建砂混合獲得對應的橡膠顆粒-砂混合料，分別編號為M1-2、M2-3、M3-4、M4-6.表1為橡膠顆粒-砂混合料的基本物理性能.其中wR為橡膠摻量(質量分數，文中涉及的摻量、含水率等除特別說明外均為質量分數)，d10、d50分別表示小于該粒徑的顆粒質量占總顆粒質量的10%和50%，ρdmin為最小干密度，ρdmax為最大干密度，Cc為曲率系數，Cu為不均勻系數.

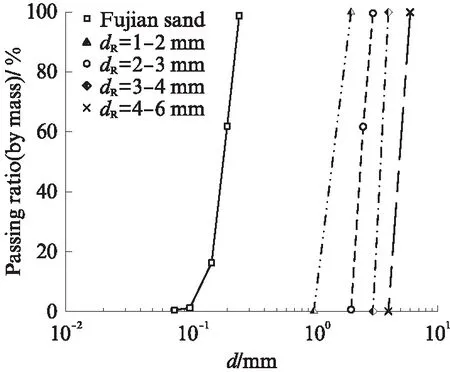
圖1 橡膠顆粒與福建砂的級配曲線

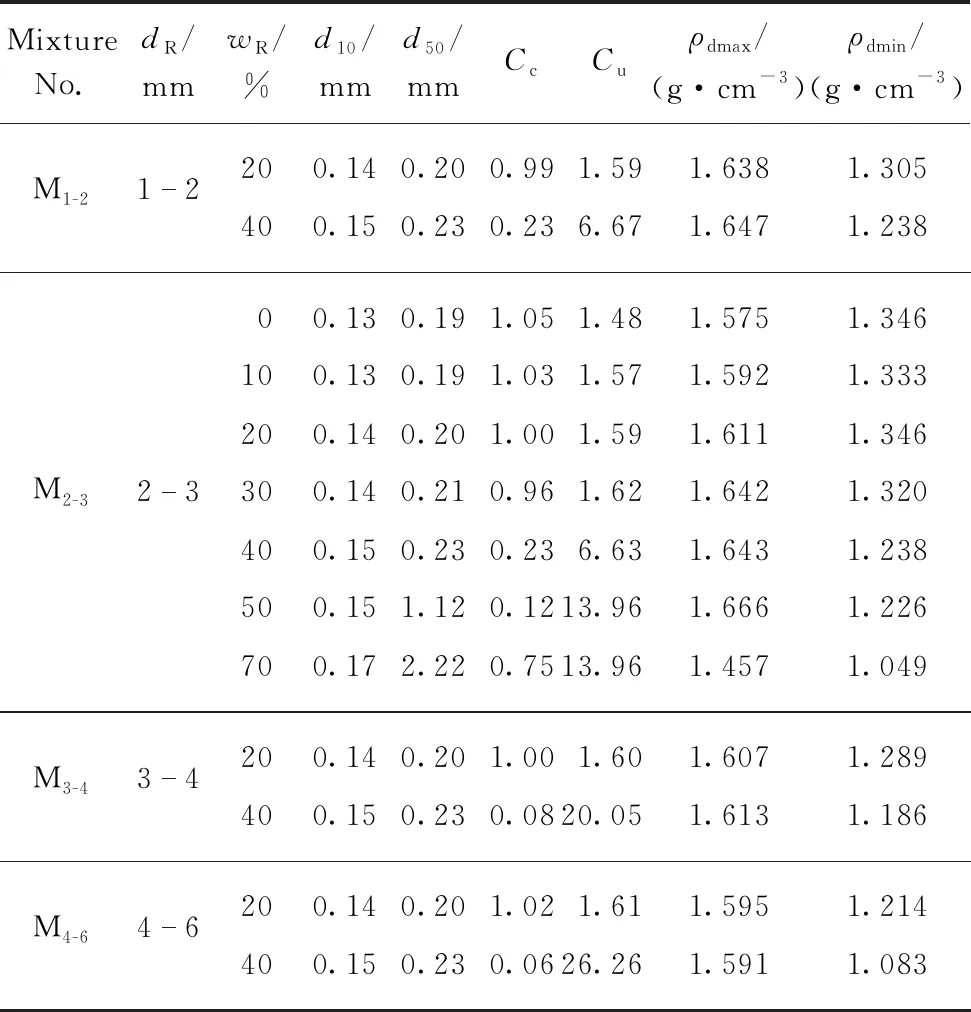
表1 橡膠顆粒-砂混合料的基本物理性能

2.2 試樣制備

試樣為φ50×100mm的實心圓柱.濕擊法多用于砂、粉砂或粉土試樣的制備，且該方法可以較好地控制試樣的孔隙比(e)，同時也能獲得較大的e值范圍[18].因此，本次試驗采用濕擊法制樣.通過多次測試，發現當試樣含水率為5%時，既能使得制備的試樣均勻性較好，又可以有效地控制孔隙比，故選擇5%的制樣含水率.整個試樣共分4層制作，每層所需橡膠顆粒和福建砂的質量按級配單獨配制.

試樣的飽和處理分為3步:(1)通15min的CO2以除去試樣中空氣.(2)從試樣底部到頂部通無氣水，直到頂部沒有氣體排出.(3)進行分級反壓飽和.測定試樣分級反壓飽和后的孔壓系數(B)，若B>0.95，即認為試樣達到飽和[19].飽和完成的試樣進行均等固結.初始有效圍壓(σ′3c)為100kPa.

2.3 試驗方案

(1)對試樣M2-3施加3個循環應力比(CSR)的循環軸向荷載，探討CSR及wR對橡膠顆粒-砂混合料液化特性的影響.

(2)控制wR=0%、20%、50%的試樣M2-3相對密實度(Dr)分別為35%、50%、60%，研究Dr對混合料液化特性的影響.

(3)分別對試樣M1-2、M3-4、M4-6施加相同CSR的循環軸向荷載，研究dR增大引起的混合料液化特性的變化.綜合考慮wR、Dr及dR的不排水循環三軸試驗工況見表2.試驗采用正弦波加載，加載頻率為1Hz.當軸向循環應力幅值為雙幅軸向應力(σd)時，施加于試樣的循環應力比CSR定義為[20]：

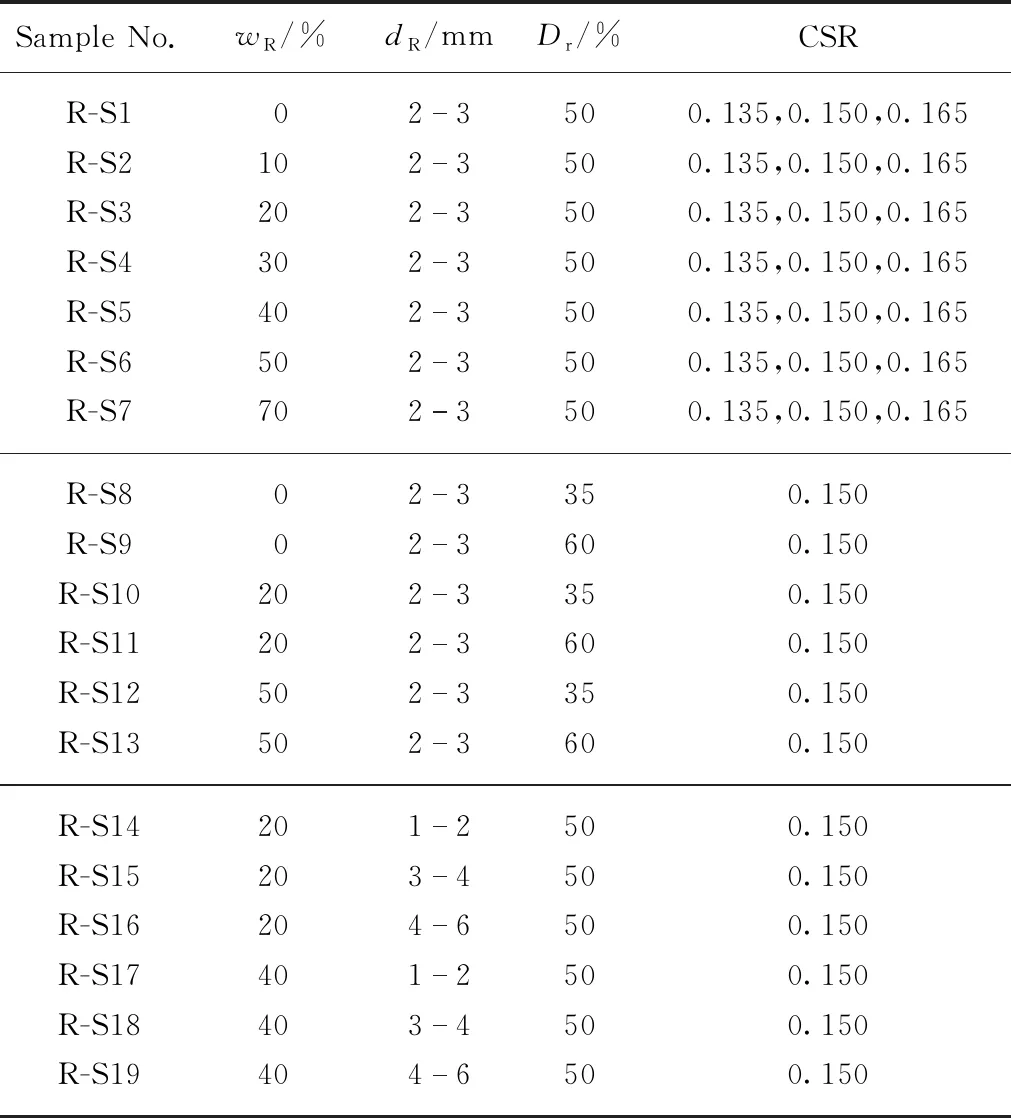
表2 不排水循環三軸試驗工況

CSR=σd/2σ′3c

(1)

3 結果與分析

3.1 典型試驗結果與液化判別

為了全面了解純砂顆粒(wR=0%)與純橡膠顆粒(wR=100%)的力學特性，在開展循環三軸試驗前，首先對顆粒進行了一系列不排水剪切試驗.考慮到與液化特性試驗結果保持可比性，控制初始有效圍壓為100kPa，Dr=50%，對應的偏應力(σ1-σ3)-軸向應變(ε)曲線如圖2所示.由圖2可見，純砂顆粒與純橡膠顆粒在不排水條件下都呈現出先剪縮后剪脹的趨勢，與之對應的峰值強度分別為451、98kPa.

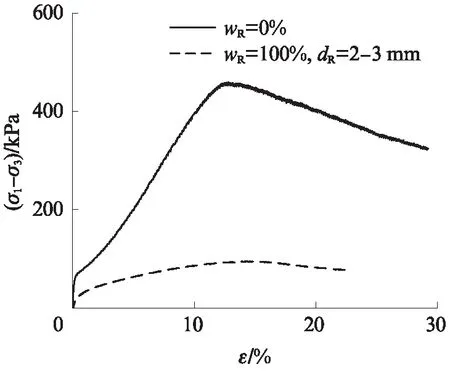
圖2 純砂和純橡膠顆粒的應力-應變關系曲線

對于土體液化機理的認識，通常有2種觀點：(1)從應力狀態出發分析土體液化，液化標志著土體的有效應力為零，土體不再具有抗剪能力[21].(2)土體液化表現為過量的變形或應變，使土體呈現出具有液體性態的流動破壞[22].由于對液化機理認識的不同，這使得飽和土體不排水循環三軸試驗的液化判別標準有2種.一是孔壓標準[23]：在循環荷載作用下試樣的Δu達到σ′3c作為液化判別標準，即孔壓比(Ru=Δu/σ′3c)達到1.二是變形標準[18]：在循環荷載作用下試樣的單幅軸向應變(εs)達到2%～3%或雙幅軸向應變(εd)達到5%作為液化判別標準.

圖3、4為試樣M2-3的典型試驗結果.由圖3、4可見：橡膠顆粒-砂混合料孔壓比Ru和雙幅軸向應變(ε)隨振次(N)的發展規律隨著wR的增加而轉變；當wR=0%～20%時，在前幾個振次Ru迅速增大，隨著N的增大，Ru增速趨于平穩，最后又急劇增加，呈現快—平穩—急劇的增長模式；當Ru<0.8時，εd保持不變且接近于0，當Ru>0.8時，εd在極少的振次下迅速增大，當Ru=1.0時，εd超過5%，這與典型的飽和砂土液化現象基本一致；當wR=30%～50%時，Ru隨振次的增大呈現“快—平穩—快”的增長模式，當Ru超過0.6后，εd隨振次增加而逐漸增大，最終超過5%；當wR=70%時，Ru隨振次的增大呈現“快—平穩”的增長模式，且增長速率逐漸降低，最終Ru穩定在0.8左右，εd在循環應力施加初期就隨N的增加逐漸增大并最終超過5%，基本上混合料表現出與純橡膠一致的力學特性.因此，通過上述分析可以認為，當橡膠顆粒摻量較小時(本文小于50%)，可將εd=5%作為橡膠顆粒-砂混合料的破壞判別標準.當橡膠摻量較大時，因橡膠顆粒的彈性變形較大，導致混合料破壞時的應變標準明顯大于5%.

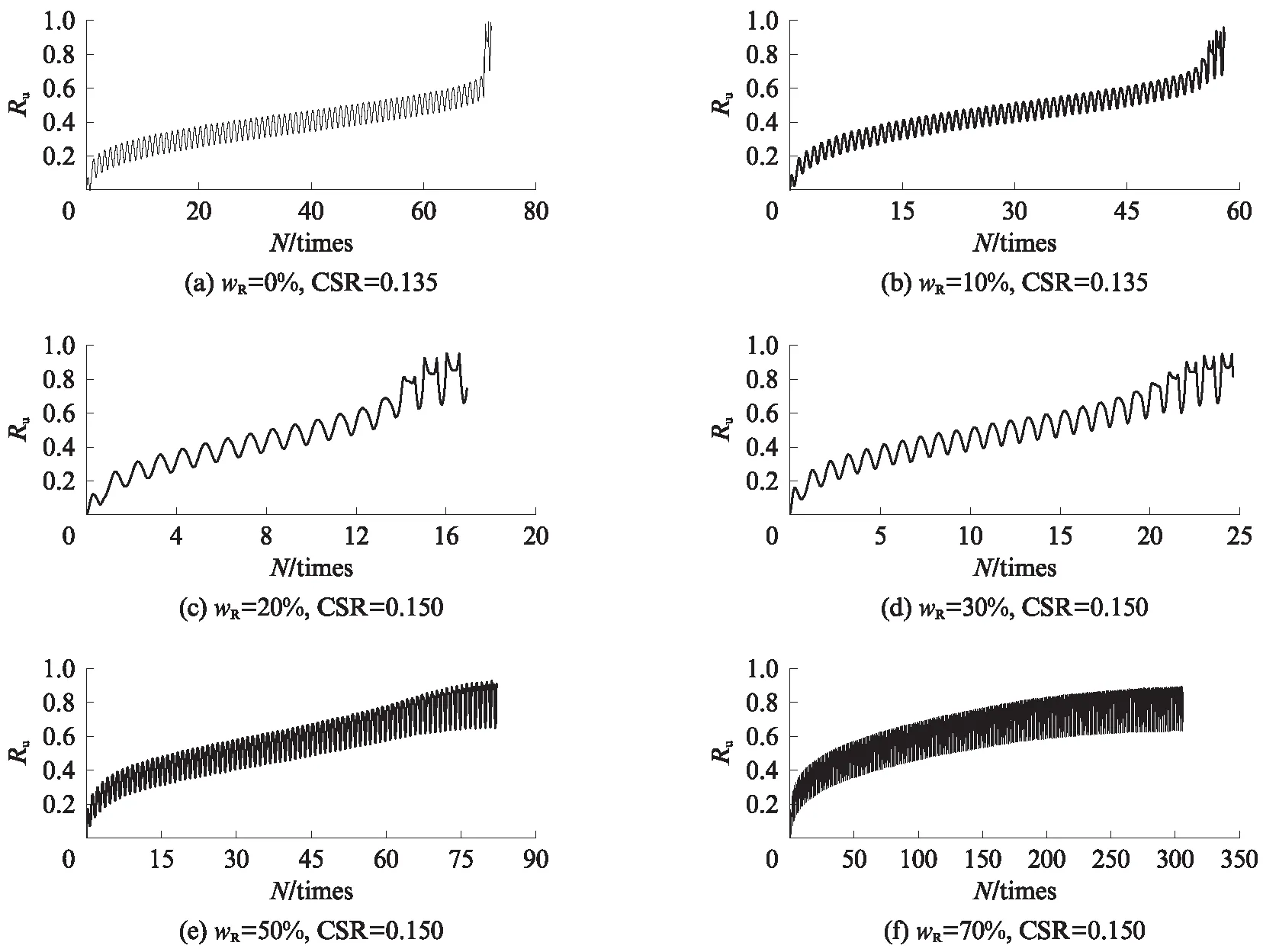
圖3 橡膠顆粒-砂混合料的孔壓比發展

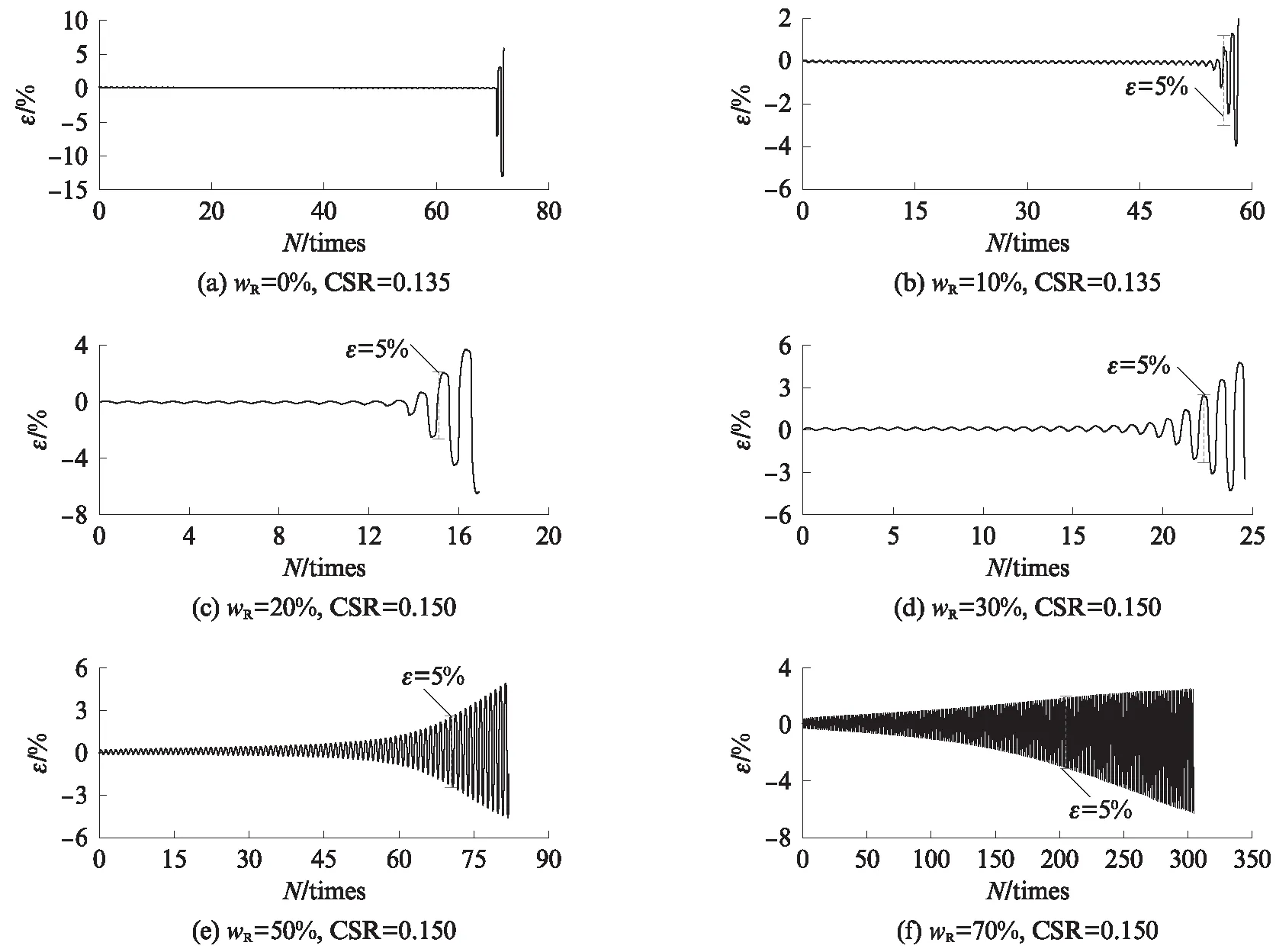
圖4 橡膠顆粒-砂混合料的軸向應變發展

3.2 動強度分析

圖5為試樣M2-3的破壞振次(Nf)與橡膠摻量的關系.由圖5可見，隨著wR的增加，橡膠顆粒-砂混合料的Nf呈先減小后增大的趨勢.這是因為：(1)當wR較小時，橡膠顆粒-砂混合料的骨架仍由砂粒組成，橡膠顆粒分散于砂顆粒之間.由于其摻量較低，因此橡膠顆粒互相無接觸，此時的橡膠顆粒不僅無法起到恢復變形的作用，還削弱了土顆粒骨架之間的接觸，因此相對于純砂其更易破壞.(2)隨著wR繼續增加，橡膠顆粒間開始接觸，逐漸形成有效骨架，在循環荷載作用下，因橡膠顆粒具有很好的可恢復彈性變形，使得橡膠顆粒土的殘余體應變累積緩慢，因此其抗液化能力逐漸提升.值得關注的是，當CSR=0.135時，Nf達到最小值時所對應的wR=40%，而當CSR=0.150或0.165時，Nf達到最小值時所對應的wR=10%.從微觀角度來判斷，產生該差異的主要原因是：當CSR較小時，橡膠顆粒開始參與力鏈傳遞所需的wR較大，而當CSR較大時，僅僅需要wR=10%，橡膠顆粒即參與力鏈傳遞，上述機理解釋還有必要通過微觀分析方法加以驗證.

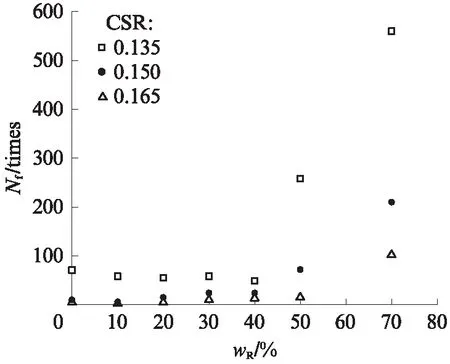
圖5 M2-3的破壞振次與橡膠摻量的關系

為了探討橡膠顆粒粒徑對橡膠顆粒-砂混合料抗液化強度的影響，圖6給出了試樣M2-3中橡膠顆粒平均粒徑(d50-R)與破壞振次的關系.由圖6可見，隨著d50-R的增大，Nf總體上呈增大趨勢.主要原因為：當d50-R較小時，單個橡膠顆粒的回彈能力有限，且更為分散，從而使得混合料較容易液化；隨著d50-R的增大，單個橡膠顆粒能夠提供有效的回彈變形能力，提高了試樣的抗剪切變形能力，從而增強了橡膠顆粒-砂混合料的抗液化強度.值得注意的是，試樣M2-3與M3-4的Nf較為接近，可能是因為這2種橡膠顆粒粒徑較為接近且跨度較小，因此有著相似的試驗結果.

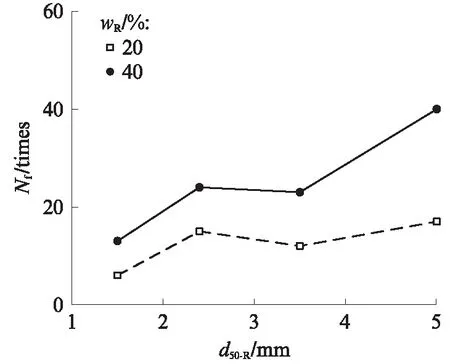
圖6 M2-3的破壞振次與橡膠顆粒平均粒徑的關系

圖7為試樣M2-3的破壞振次隨相對密度(Dr)和橡膠摻量變化的規律.由圖7可見：與已有的砂土試驗結果一致，M2-3的Nf隨Dr的增大而增大.此外，隨著wR的增大，Dr對Nf的影響逐漸削弱.分析認為：當wR較小時，橡膠顆粒-砂混合料的力學特性更接近于純砂，顆粒骨架會隨Dr的提升而增強；而當wR增加時，由于橡膠顆粒具有易變形的特性，無論Dr高低，在相同固結壓力作用下，都會趨向于同一密實狀態，從而導致對Dr對Nf的影響減弱.

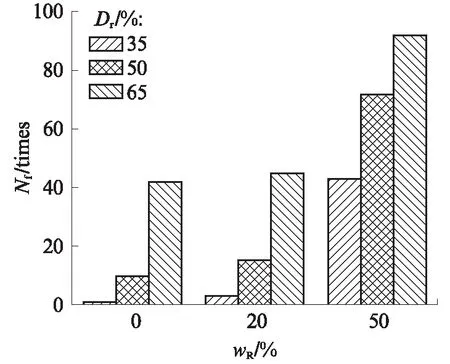
圖7 M2-3的破壞振次與相對密度的關系

3.3 橡膠顆粒-砂混合料的應變分析

圖8為橡膠顆粒-砂混合料雙幅軸向應變幅值(εdmax)與循環振次比(N/Nf)的關系曲線.由圖8可見：在各試驗條件下，εdmax都隨N/Nf的增加而增大，但其增加速率有顯著差異；當N/Nf相同時，εdmax隨wR的增加而增大.這是由于橡膠顆粒具有模量低、易變形的特性，當wR增加時，土體更易發生變形.由圖8(a)可見：當wR=0%～20%時，在N/Nf小于0.8時，εdmax增長緩慢且趨近于0，而當N/Nf超過0.8時，εdmax在較少振次內迅速增大并超過5%，這與典型的砂土軸向變形發展規律基本一致；當wR=30%～50%時，εdmax隨N/Nf的增長速率逐漸增大，且wR增加會顯著降低該增長速率，此時，橡膠顆粒-砂混合料的變形特性從類砂土向類橡膠顆粒轉變；當wR=70%時，εdmax隨N/Nf的呈線性增大，橡膠顆粒- 砂混合料的變形能力顯著高于其他工況，且加載初始階段便存在1%量級的εdmax，這表明當wR超過70%后，橡膠顆粒-砂混合料骨架由橡膠顆粒控制，砂顆粒基本不參與力鏈傳遞.圖8(b) 給出了Dr對wR=50%的試樣M2-3εdmax發展規律的影響.當N/Nf為定值時，橡膠顆粒-砂混合料的εdmax隨Dr的降低而增大，且εdmax隨N/Nf的增長速率也隨Dr的增大而降低，產生該現象的原因是：隨著Dr的增大，橡膠顆粒-砂混合料更加密實，顆粒接觸面積增大，從而增大混合料的抗變形能力.圖8(c) 描述了橡膠粒徑dR對橡膠顆粒-砂混合料εdmax發展規律的影響，隨著dR的增大，εdmax減小.此外，試樣M2-3和M3-4的εdmax基本一致.

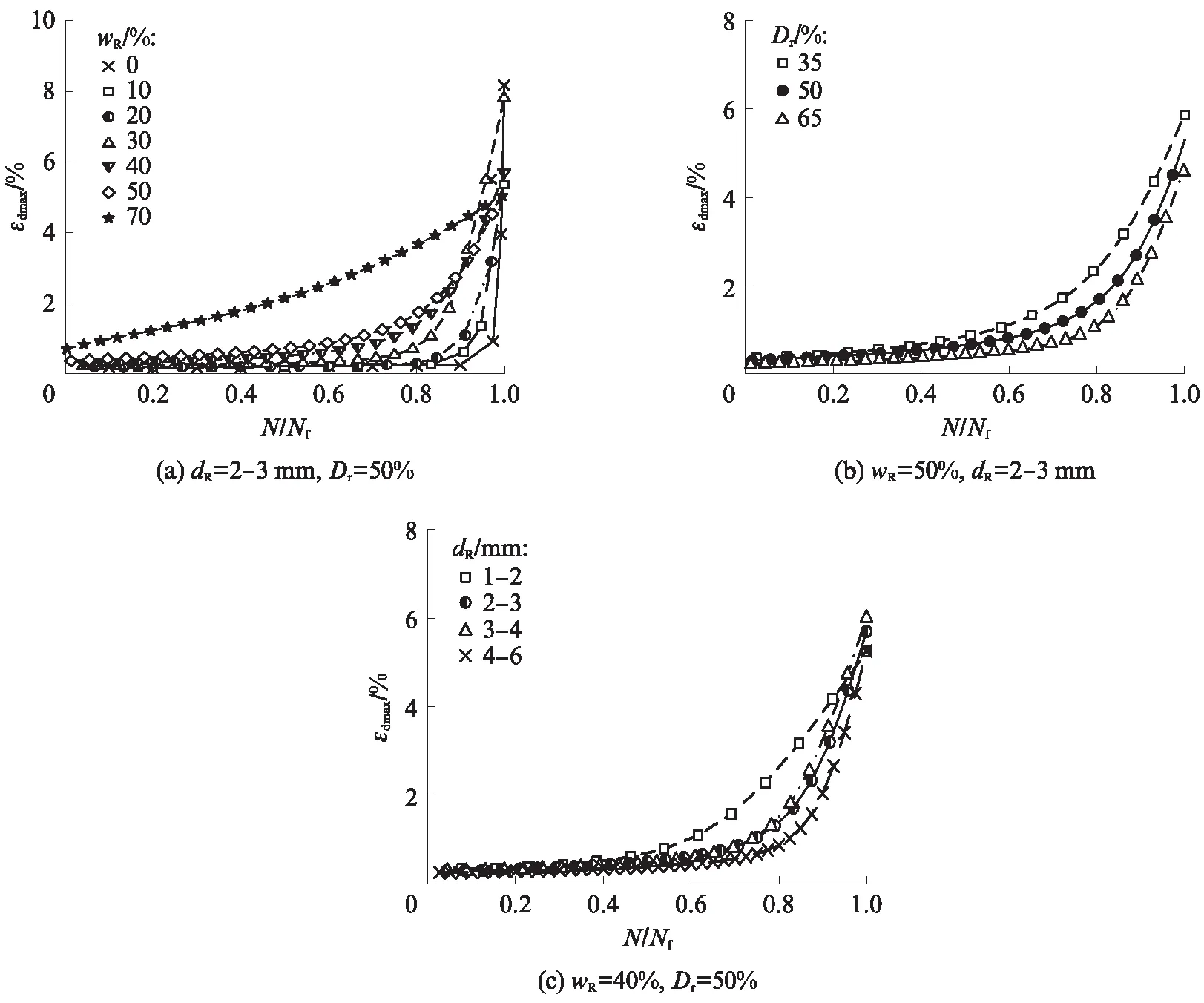
圖8 橡膠顆粒-砂混合料的雙幅軸向應變幅值與循環振次比關系

3.4 橡膠顆粒-砂混合料滯回耗能特性分析

滯回圈(應力-應變曲線)不僅描述了橡膠顆粒-砂混合料的應力-應變關系，還可由此計算出模量、阻尼比等重要的動力學參數.圖9為wR對橡膠顆粒-砂混合料應力-應變關系曲線的影響.由圖9可見：當εdmax相同時，wR越大，橡膠顆粒-砂混合料的滯回圈越規整狹長，拉、壓應力產生的應變越對稱，這表示混合料有著較好的彈性變形恢復能力；當wR較低時，滯回圈出現較為明顯的不對稱性.此外，隨著wR的降低，橡膠顆粒-砂混合料滯回圈面積逐漸增大，這意味著橡膠顆粒-砂混合料吸收了更多的能量.相反，wR較高的橡膠顆粒-砂混合料滯回圈面積較少，說明該振次吸收的能量較少，即該振次對橡膠顆粒-砂混合料的破壞作用更小.

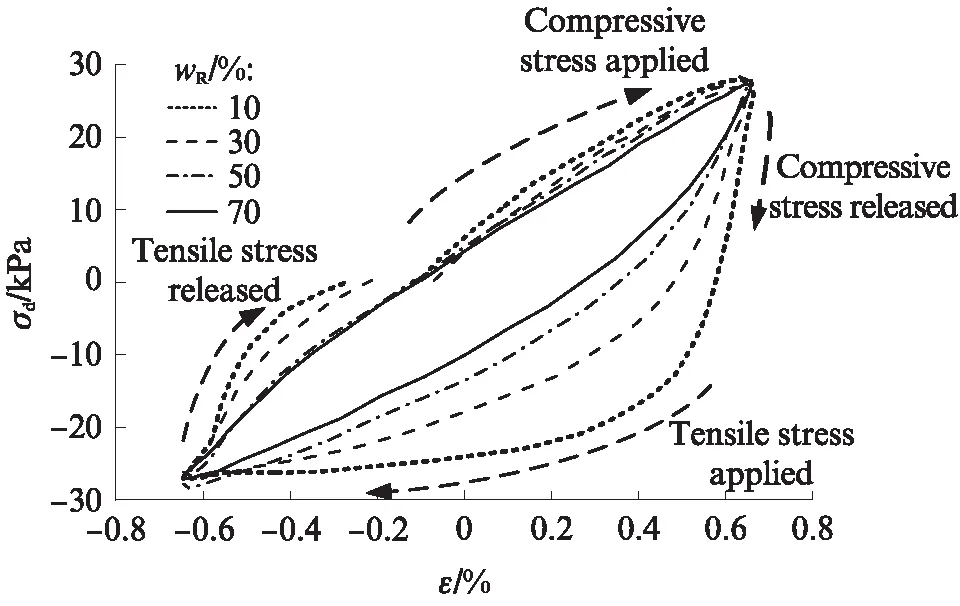
圖9 相同應力-應變下的滯回圈對比

Figueroa等[24]提出用滯回圈面積的大小來表征土單元的能量耗散，將加載過程中所有能量耗散相加，即得到土單元在液化時總的能量耗散.圖10為循環荷載作用下試樣M2-3的累積能量耗散(W).由圖10可見：當wR=0%～20%時，不同CSR作用下試樣M2-3在各εdmax水平下的W基本一致；當wR超過30%時，不同CSR作用下試樣M2-3在各εdmax水平下的W有所差異，且該差異隨wR的增加逐漸增大.這是因為隨著wR的增大，橡膠顆粒-砂混合料的彈性恢復變形能力逐漸增大，從而使得達到指定εdmax水平所需的W隨CSR變化越顯著.

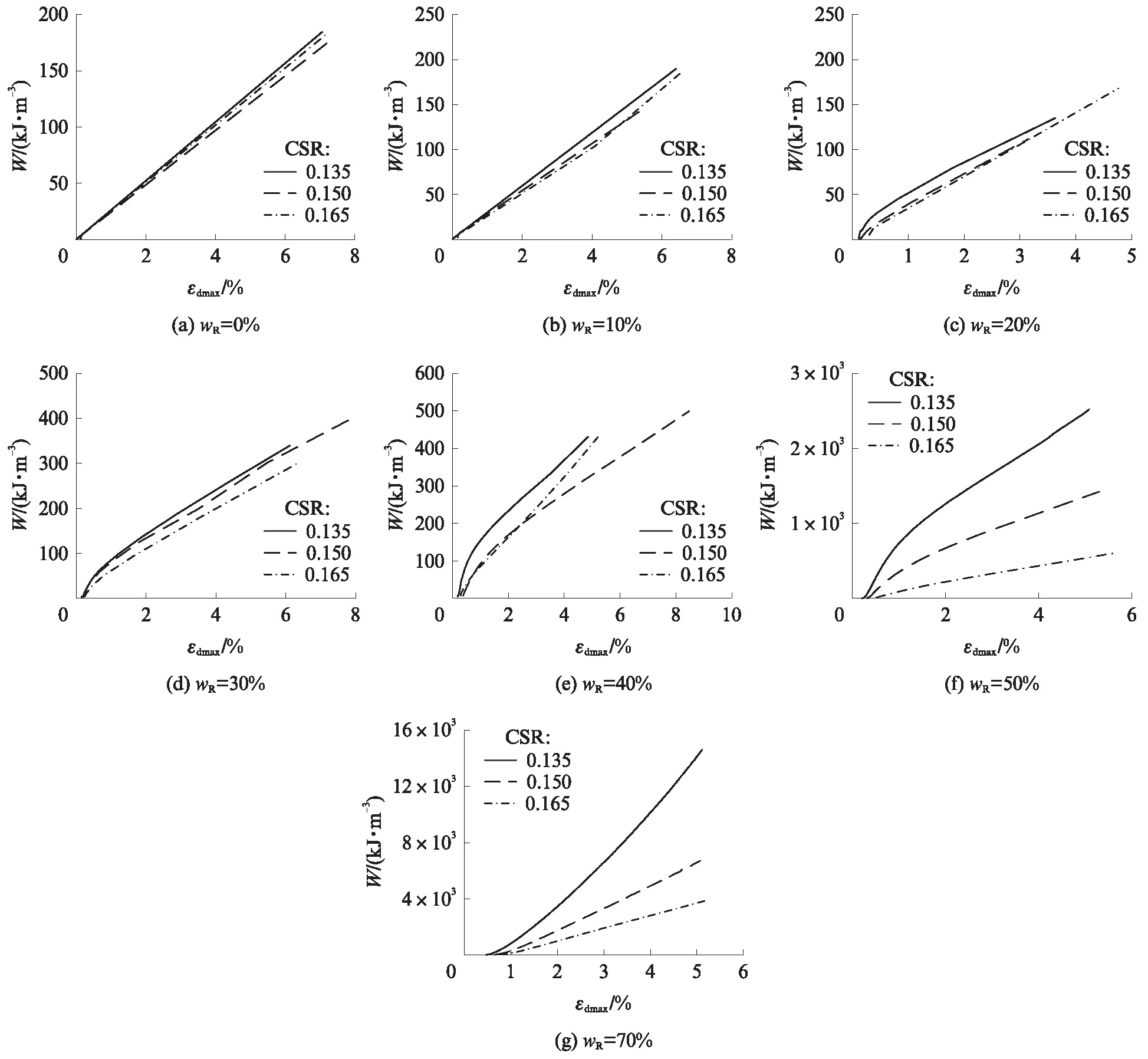
圖10 不同工況下M2-3試樣的累積能量耗散

圖11為各CSR作用下試樣M2-3達到破壞標準所需的累計能量耗散(Wf)與橡膠摻量的關系.由圖11可見：當CSR相同時，Wf隨wR的增大呈非線性增大，wR越大，Wf的增大速率越大；當wR=0%～20%時，各CSR作用下的Wf基本一致；當wR大于30%時，各CSR作用下的Wf開始產生明顯差異，且CSR越大，Wf的差異越明顯.

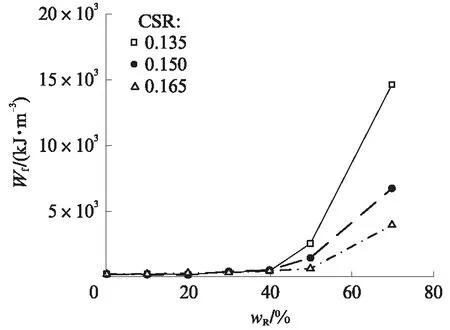
圖11 試樣M2-3達到破壞標準所需能量與橡膠含量的關系

結合圖3、4、8(a)、11可知，當wR=0%～20%時，橡膠顆粒-砂混合料表現出來的主要動力學特性與純砂相似，即可認為其動力學特性主要由砂土組構決定；當wR=30%～50%時，隨wR的增大，橡膠顆粒-砂混合料的力學特性由砂土向橡膠顆粒轉變；當wR超過70%時，橡膠顆粒-砂混合料的力學特性與純橡膠顆粒一致，此時力學特性主要由橡膠顆粒組構決定.

4 結論

(1)隨著橡膠摻量wR的增加，橡膠顆粒-砂混合料呈現不同的孔壓和應變增長規律，總體上當wR較少(小于50%)時，可以將雙幅軸向應變εd=5%作為橡膠顆粒-砂混合料的破壞判別標準.wR較大時，橡膠顆粒-砂混合料破壞對應的應變判別標準明顯大于5%.

(2)橡膠顆粒-砂混合料破壞振次(Nf)隨著wR的增大呈現先減小后增大的趨勢.循環應力比不同時，Nf達到最小值所需的wR有所差異.其他條件一致時，Nf隨相對密實度(Dr)及橡膠粒徑(dR)的增大而增大.雙幅軸向應變幅值(εdmax)隨循環振次比(N/Nf)的增大而增大，隨著wR的增大，εdmax與N/Nf的相關性從強非線性向線性轉變，且當N/Nf為定值時，wR的增大、Dr及dR的減小都會引起εdmax增大.

(3)橡膠顆粒-砂混合料達到破壞標準所需的累積能量耗散(Wf)隨wR的增大呈非線性增大，wR越大，Wf的增大速率越大.此外，當wR=0%～20%時，各CSR作用下橡膠顆粒-砂混合料的Wf基本一致；當wR大于30%時，各CSR作用下橡膠顆粒-砂混合料的Wf開始產生明顯差異，且CSR越大，Wf的差異越明顯.

(4)當wR=0%～20%時，橡膠顆粒-砂混合料表現出來的主要動力學特性與純砂相似；當wR=30%～50%時，隨著wR的增大，橡膠顆粒-砂混合料的動力學特性由砂土向橡膠顆粒轉變；當wR超過70%時，橡膠顆粒-砂混合料表現出的動力學特性與純橡膠顆粒一致.