一道2020年全國大學生數學競賽題的多種推廣

萬安華

(中山大學 數學學院，廣州510275)

1 引 言

高等數學是高校本科非數學類專業的一門重要基礎課.教師如何在課堂教學中傳授數學思想與數學方法是值得深入研究的課題[1].在高等數學的課堂教學中，選取富有啟發性的例題進行適當的延拓，有利于培養同學們的創新思維能力[2]. 教師將每年的全國大學生數學競賽試題及時引入相關章節的課堂教學中，并且通過綜合運用數學方法將競賽題進行多角度的延拓，不僅加強了例題的新穎性，也極大地激發了同學們的學習熱忱.

2 分析與推廣

引言中這道競賽題中出現了兩個底和指數互換位置的冪指函數[f(x)]g(x)和[g(x)]f(x). 對于一般的冪指函數u(x)v(x)(u(x)>0，u(x)不恒為1)，可將其轉化為u(x)v(x)=ev(x)lnu(x)，由此來理解和處理冪指函數相關的數學問題. 當u(x)v(x)→1(在自變量x的某種變化趨勢下)時，運用等價無窮小代換et-1～t(t→0)[3]， 可得

u(x)v(x)-1=ev(x)lnu(x)-1～v(x)lnu(x).

再進一步地推廣為更加廣泛的情形

因此只需考慮最后一種推廣情形，前面的幾種情形均可作為其特例而導出.其次，擬對冪指函數[f(x)]g(x)和[g(x)]f(x)的底作推廣，可考慮一般的

綜上分析，可將第一種推廣思路和第二種推廣思路結合起來，直接考慮包括了上述兩種推廣方向的一般情形

最后，還將考慮一般情形的

這一類型包括了

為特例，而此特例又包括了

為其特殊情況.

下面展開對上述幾種推廣情形的具體分析，并導出相應的結果.

2.1 對指數和底均作延拓后的一般情形

設f(x)，g(x)，Φ(x)，Ψ(x)，φ(x)，φ(x)在x=x0的某一鄰域U內有定義，對任意x∈U，

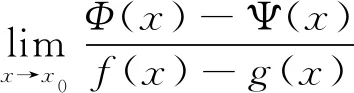
一方面

另一方面

因此

(1)

特例1設f(x)，g(x)，Φ(x)，Ψ(x)在x=x0的某一鄰域U內有定義，對任意x∈U，

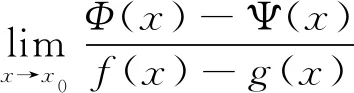
(2)

注1 引言中的競賽題即為特例1在Φ(x)=f(x)，Ψ(x)=g(x)時的特殊情況，由(2)式即得

(3)

特例2設f(x)，g(x)，φ(x)，φ(x)在x=x0的某一鄰域U內有定義，對任意x∈U，

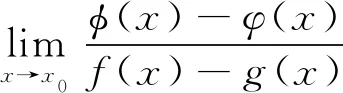
(4)

由特例2，可以得到下面的推論.

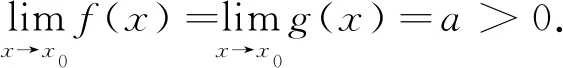
(5)

證由特例2，立即可得

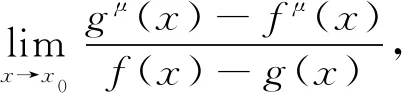
因此

(6)

注2 作為(6)式的直接應用，卻可以得到一個更一般的結論，即對于任意的實數λ≠(lna)-1，有

進一步地，還可以由特例2推出比推論1更為廣泛的如下結論成立.

推論2設f(x)，g(x)在x=x0的某一鄰域U內有定義，對任意x∈U，f(x)≠g(x)，且

4、整地改土：由于項目區為沙質土，土壤有機質含量低，需要對土地進行全面整治，通過人工施肥、深耕等措施，提高土地生產力。

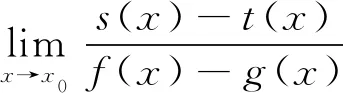
(7)

證在特例2中令φ(x)=[g(x)]s(x)，φ(x)=[f(x)]t(x)，則c=ad.由(4)式可得

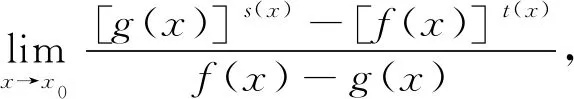
因此

以下是推論2的幾個特例：

(iii) 推論2 中當s(x)=fr(x)，t(x)=gr(x)(其中r是任意實數)時，首先由(4)式可得

接下來，由(7)式，立即可以得到

(8)

推論3設f(x)，g(x)在x=x0的某一鄰域U內有定義，對任意x∈U，f(x)≠g(x)，且

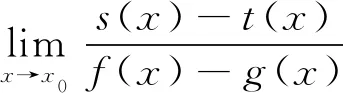
(9)

由推論3，立即可以得到以下結果：

2.2 推廣到對數函數的一般情形

設f(x)，g(x)，Φ(x)，Ψ(x)，φ(x)，φ(x)在x=x0的某一鄰域U內有定義，對任意x∈U，

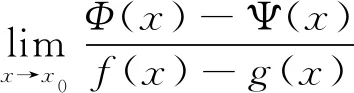
一方面

另一方面

因此

(10)

由上面的(10)式，立即可以得到以下特例.

特例3設f(x)，g(x)，Φ(x)，Ψ(x)在x=x0的某一鄰域U內有定義，對任意x∈U，

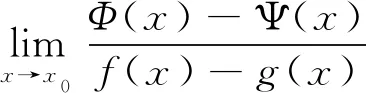
(11)

特例4設f(x)，g(x)在x=x0的某一鄰域U內有定義，對任意x∈U，

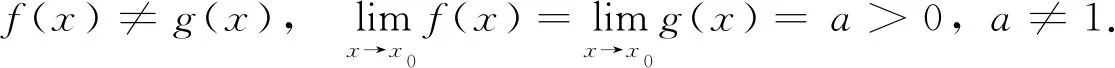
則

(12)

3 結 論

本文對最近第十二屆全國大學生數學競賽(非數學類)預賽中的一道試題從多個角度進行了延拓與縱深推廣，拓展了教學內容.在高校數學課程教學中，恰當地引入與授課章節內容貼合的數學競賽題，豐富了數學課堂的例題庫.教學中對數學競賽題進行延伸性改編，不但激發了同學們的學習熱忱和積極參與競賽的熱情，而且幫助了同學們學會去發現新問題、綜合運用數學方法解決問題，由此提升了創新思維與科研能力.

致謝作者非常感謝相關文獻對本文的啟發以及審稿專家提出的寶貴意見.