關于獨頭巷道爆破掘進通風的探討①

高文蛟，梁俊奇，徐家俊，夏方順

（華北科技學院 研究生院，河北 廊坊 065201）

目前以炸藥量來計算獨頭巷道爆破掘進通風風量的方法是在控制體理論的基礎上提出的，即將爆破后所產生的炮煙視為一個規則的控制體，單純以控制體內炮煙濃度達到安全標準時所需風量來計算巷道爆破后所需風量［1－2］。而炮煙實際排除過程是炮煙被壓入的新鮮空氣不斷置換的同時不斷擴散稀釋的過程。本文對現有通風風量計算公式進行了剖析，指出了計算方法中存在的缺陷和不足；然后從基本理論出發并結合現有標準，推導出新的獨頭巷道爆破掘進通風量計算公式，并結合現場實測數據，對新公式進行了驗證。

1 壓入式通風風量計算方法

獨頭巷道炮煙排除過程的風量計算方法通常存在兩種不同的觀點。一是認為炮煙的排除是靜態稀釋過程，將爆破后的炮煙視為一個規則的控制體，單純以控制體在規定時間內炮煙濃度達到安全標準時所需風量來計算，在此基礎上提出了依據炸藥量的風量計算公式［3－5］。由于炮煙的排出不是單純的稀釋過程，爆破后的炮煙在被壓入的新鮮風流推動下與前面的空氣混合稀釋的同時，也是控制體拉長變形與后面壓入的新鮮空氣混合稀釋的過程，此觀點忽略了后面空氣的作用，使用此方法計算的風量比實際所需風量偏大。二是認為炮煙的排出既有主風流的運移作用，又有風流的紊流擴散作用，是一個綜合作用的過程。這與實際的炮煙排出過程較為接近。根據這一觀點，國內外學者對獨頭巷道的炮煙排出過程進行了比較詳細的研究。前蘇聯學者沃洛寧在紊流擴散和紊流變形理論的基礎上，提出巷道斷面上距軸線r處的風速公式［2］：

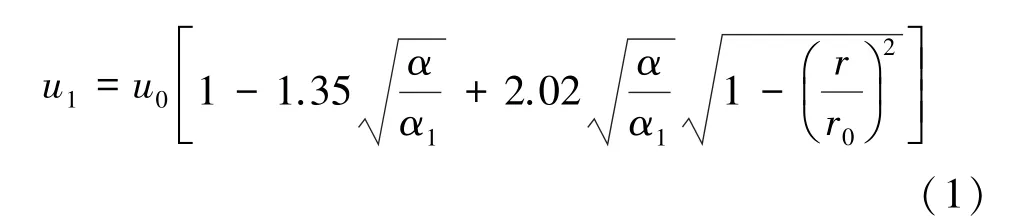
式中u1為巷道斷面距軸線r處的風速；u0為巷道斷面上的平均風速；α為巷道的摩擦系數，在一般礦山條件下α取值范圍0.001 5～0.002 5；α1為實驗常數，取0.003 2；r0為巷道斷面的半徑。

將α和α1代入式（1），得出簡化后的風速公式：

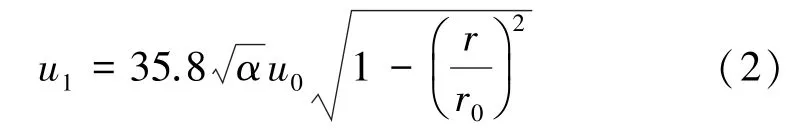
根據以上巷道內風速分布規律，可以推算通風一段時間后巷道內炮煙的近似軌跡，同時又有：

式中c為炮煙濃度；c0為炮煙初始濃度；l1為掘進巷道長度，m；l a為風筒末端到工作面的距離，m；I為風量交換倍數，取I＝Qt／V［2］，其中Q為風量，t為通風時間，V為通風空間體積。

隨后根據濃度關系以及風速公式，進而推導出風量Q計算公式［2］：

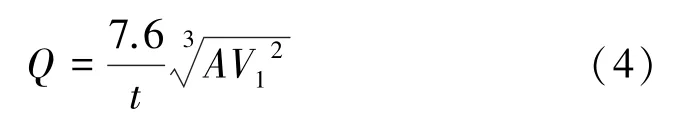
式中A為爆破炸藥量，kg；V1為巷道長l1時的體積。

上述公式的推導過程以炮煙拋擲帶的長度和風筒距掘進工作面長度相等為前提，而實際生產過程中，風筒末端距掘進工作面的距離一般都小于炮煙拋擲帶的長度，因此吳中立結合這一情況對風量公式進一步分析，得出濃度分布關系［2］：

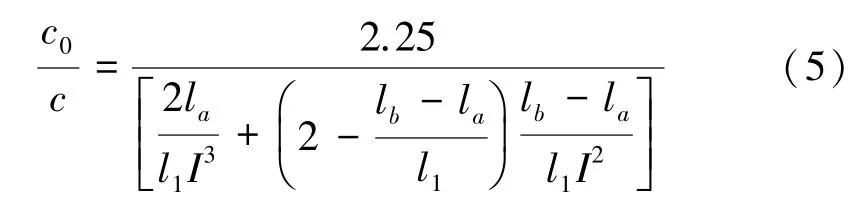
結合風速公式得出風量計算公式：

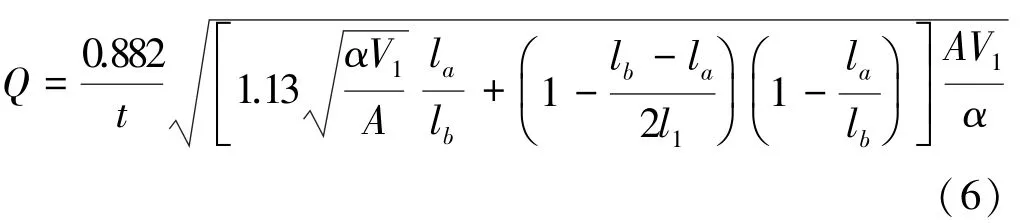
式中l b為炮煙拋擲帶長度，m。l b由炸藥量決定，目前礦山多為電雷管起爆，所以

而文獻［1］運用礦井空氣動力學，通過建立實際的梯形木風筒和圓形鐵風筒模型，并對模型中的風速分布進行測定，提出了濃度關系式：

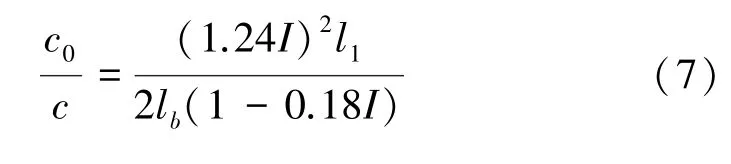
隨后，文獻［6］在此基礎上推導出風量計算公式：

對以上3種風量計算公式進行分析，沃洛寧和吳中立的風量公式是以紊流擴散和紊流變形理論為基礎進行分析和推導的，所不同的是炮煙拋擲帶長度l b和風筒距掘進工作面長度l a的差異性，吳中立對沃洛寧公式進行了相應修正，但其風量計算公式太過復雜，應用并不方便。而文獻［1］認為，在炮煙排除過程中，風流的紊流擴散作用與紊流變形作用相比居次要地位，可忽略不計，并進行了相應的測定得到風速及濃度計算公式。王一民在此基礎上得出風量計算公式（8），但由于王英敏在分析炮煙排出過程時也沒有考慮紊流的擴散作用，因此公式（8）的計算風量也不能準確地表示實際所需風量。

另外，炮煙所含成分除了CO外還存在毒性更大的氮氧化合物，而CO相較于氮氧化合物更加穩定，根據國家標準，分析過程中將炮煙中的有毒有害氣體統一折算為CO濃度來進行分析［7－8］。以前我國煤礦使用的大多是粉狀銨梯炸藥，根據國家技術標準，其爆炸后釋放出的有毒氣體量是以100 L／kg進行計算的，而現在我國煤礦使用的大多為含水炸藥，其爆炸后釋放的有毒有害氣體量已降為40 L／kg［9－11］。因此關于獨頭巷道炮煙排除的風量計算公式需要進一步探討修正。

2 風量計算修正

考慮到炮煙排出過程是紊流變形與紊流擴散的共同作用，在后續的分析過程中以沃洛寧的風速公式為基礎，結合吳中立分析的實際生產過程中炮煙拋擲帶長度l b大于風筒距掘進工作面長度l a這一情況，參考文獻［1］所得炮煙濃度分布關系對炮煙的排出過程進行分析，同時根據現行國家標準規定的最新參數［10］要求，對風量計算公式進行簡化修正。

圖1為炮煙運動示意圖。

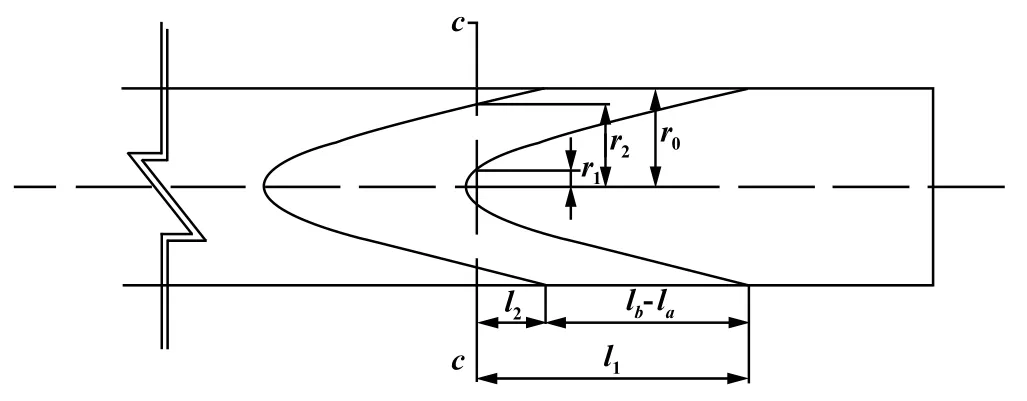
圖1 炮煙運動示意圖

根據巷道斷面風速分布公式（2）得到炮煙波內外界面隨通風時間變化的軌跡方程為：

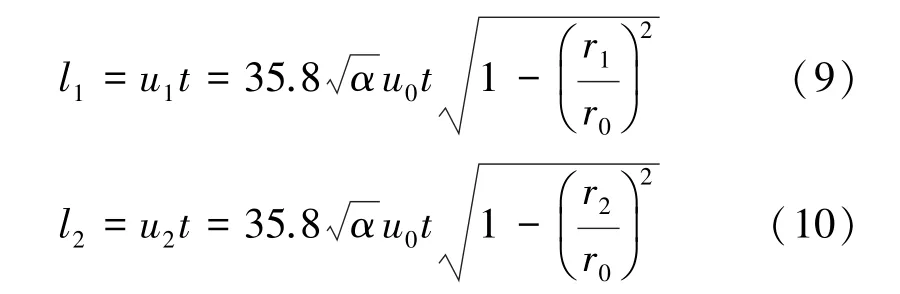
式中r1為c?c斷面上炮煙內層距軸線距離；r2為c?c斷面上炮眼外層距軸線距離；l1為內層行走至獨頭巷道c?c斷面的距離；l2為外層行走至獨頭巷道c?c斷面的距離。

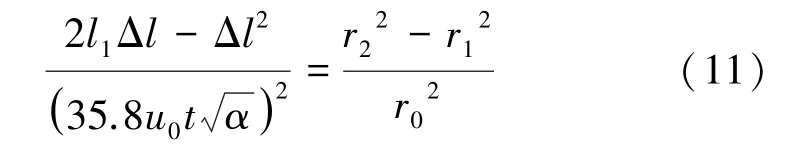
因為任意斷面上的炮煙平均濃度c與原始濃度c0之比為代入式（11）得到截面濃度與通風時間的關系式為：

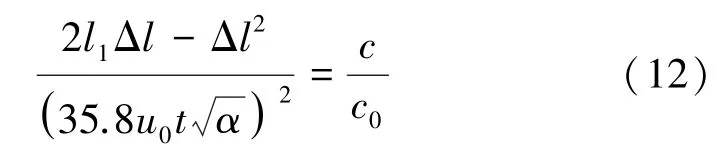
根據文獻［2］，爆破后炮煙初始濃度為：

式中b為炸藥的炮煙發生量。

以目前我國煤礦許用炸藥乳化炸藥的炮煙發生量（以CO計）為40 L／kg代入式（13）得：

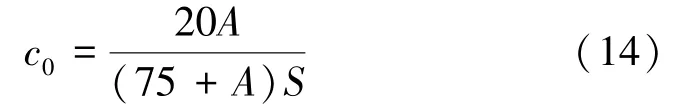
將式（14）代入式（12）得到通風過程中巷道任一截面平均風速，進而得到風量計算公式為：

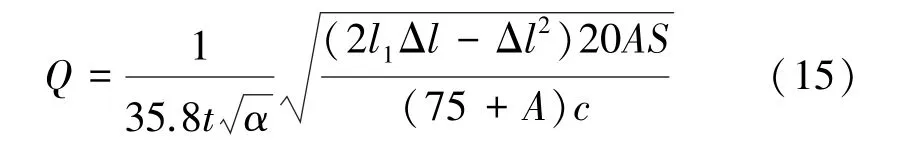
式中S為巷道斷面積。

同時根據現有炸藥的炮煙發生量（以CO計）為40 L／kg這一變化，對先前學者推導的風量計算公式（3）、（5）、（7）進行修正得到修正后的公式為：

3 現場試驗

為了對獨頭巷道爆破掘進過程中炮煙的濃度變化規律有一個直觀的認識，并對新推導風量計算公式的合理性進行驗證，本文結合工程實況進行了現場數據實測試驗。

3.1 試驗巷道概況

試驗在某礦專用行人巷進行，該巷道為煤層井下行人巷，位于上山掘進段，巷道為矩形斷面，尺寸為3.5 m×3.2 m。該專用行人巷掘進期間采用壓入式通風，選用FBD?NO 6.0型、功率11 kW的2臺軸流式對旋風機，全風壓供風量780 m3／min，出口風量340 m3／min，入口風量350 m3／min，供風量范圍200～380 m3／min。

3.2 測點布置

此次試驗選用操作簡單、攜帶方便且具有連續自動記錄數據功能的YA?1001P系列便攜式單一氧化碳檢測儀測定CO濃度，其量程為0～5‰。為了對專用行人巷掘進爆破后炮煙（只考慮CO）擴散進行實時監測，選取距掌子面30 m、50 m、70 m、90 m、110 m共5個斷面進行了實測。

同時為了研究同一斷面上的炮煙濃度變化情況，在每個斷面上布置兩個測點，一個位于巷道軸線位置，另一個靠近巷道壁，測點的具體布置情況見圖2。

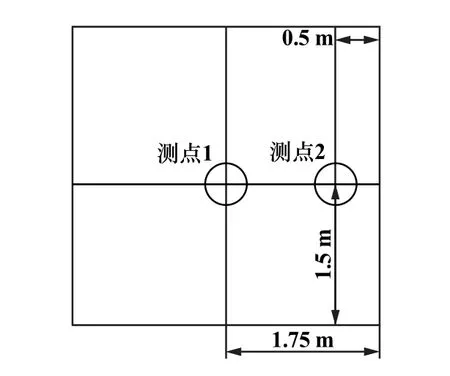
圖2 測點位置示意圖

3.3 試驗條件

此次試驗采用全斷面一次起爆，前后共進行了3次測試，試驗時的詳細工況如表1所示。其中，巷道斷面面積11.2 m2，風量380 m3／min，起爆方式均為正向起爆，炸藥種類均為三級煤礦許用乳化炸藥。

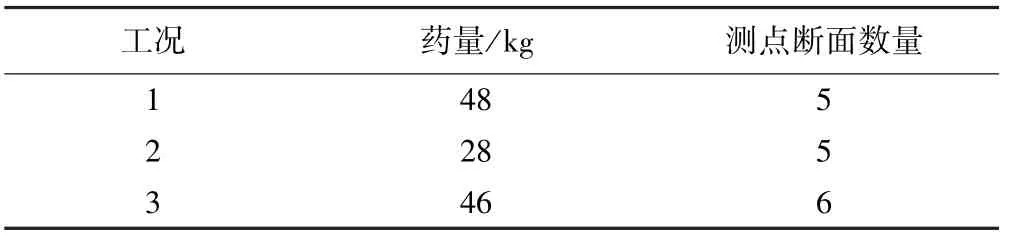
表1 試驗工況表

3.4 試驗數據分析

3次試驗不同斷面的2個測點CO濃度峰值隨距離變化曲線如圖3所示。

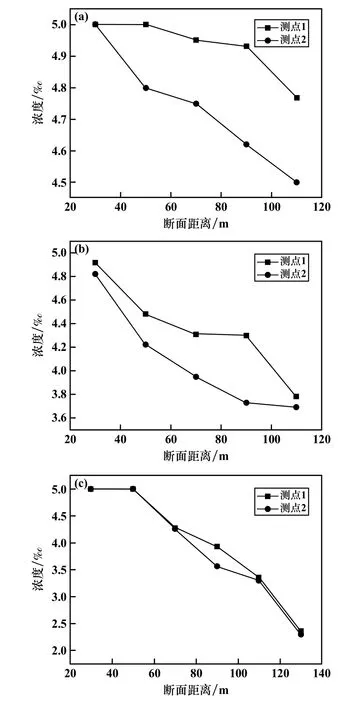
圖3 不同巷道長度的計算風量

從圖3分析可得：

1）在炸藥量不同的3種工況中，除工況3測點1和測點2的差距不明顯外，其余各個工況下同一斷面處測點1濃度總大于測點2，且就峰值濃度下降速度來講，測點1峰值濃度降低速度要小于測點2，這與理論分析所得炮煙濃度分布規律較為相似，即靠近巷道軸線位置處的CO濃度要大于靠近巷道壁的CO濃度。這是由于位于巷道軸線位置處的測點1處風流速度要大于測點2，測點1處CO濃度降低主要受紊流變形作用，而靠近巷道壁的測點2風速較低，其濃度降低過程既有紊流變形又有擴散作用，是一個綜合的過程。由此可知，為了使CO濃度隨距離降低得更多，就要降低通風速度使得炮煙中的CO能充分地參與擴散稀釋作用。因此，獨頭巷道爆破掘進時，為了降低炮煙帶來的危害、保護井下施工人員的身體健康以及有效控制生產成本，應根據爆破工藝和現場實際情況，采用適當的通風風速，而不能一味通過提高風量來解決問題。

2）分析發現工況1和工況3出現巷道斷面30 m和50 m處CO濃度峰值相同的問題，分析其原因是此次測量所選用的儀器量程有限，導致炸藥量較大時工況1和工況3的前兩個斷面（A斷面和B斷面）測點數據出現失真，實際A斷面濃度峰值要大于B斷面。

為對新推導風量計算公式的合理性進行分析和驗證，結合以上分析結果，排除失真數據，選用工況2的炸藥量及巷道條件，取通風時間15 min，巷道長度為掌子面到回風聯巷長度，風筒距掌子面距離均為10 m，代入公式（15）～（18），計算得到炮煙濃度達到安全濃度時所需的風量見表2。

表2 風量計算結果

由表2數據可知，各個風量計算公式所計算的風量要遠小于實際風量，為進一步分析各公式的區別，將表2中各公式計算風量分別代入各自的濃度公式（3）、（5）、（7）和（15）進行計算，得到對應的風量下不同斷面處的CO濃度分布情況見表3。隨后將各計算風量下所得巷道中的CO濃度分布規律與實際測得的濃度分布情況進行對比分析。

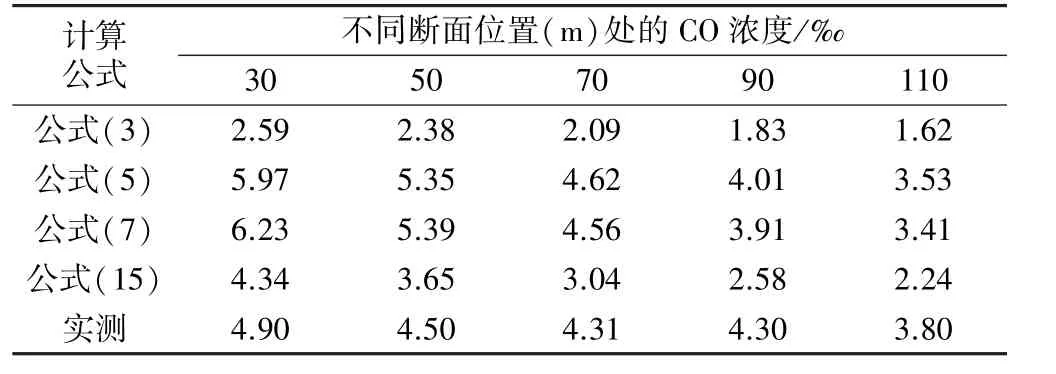
表3 工況2條件下CO濃度峰值

由表3分析可得：

1）公式（5）和（7）在70 m之前的計算濃度過大，且遠大于實測濃度，雖然整體表現出濃度減少的趨勢，但70 m之前的濃度變化顯然與實測不符，當通風風量減少時，炮煙運移速度減緩，炮煙擴散作用有所增強。先前公式在理論推導過程中只考慮風流的紊流變形作用而忽略了炮煙的紊流擴散作用，導致該公式前期的計算濃度高于實測濃度，且公式（5）和公式（7）所計算的風量要遠小于實驗風量，考慮到擴散作用的影響，后期的濃度峰值并不會與實測濃度接近；公式（3）的計算濃度遠小于實測濃度，且濃度降低速度過快，由于該公式在推導過程中以l b＝l a為前提，炮煙首先在風筒出口至掘進工作面范圍內與新鮮風流發生一定的置換稀釋后才向外排出，從而導致后續各個巷道位置處計算的炮煙濃度要遠小于實測濃度，而在實際生產過程中多數情況下l b＞l a，因此，該公式同樣與實際生產情況不符；公式（15）前期所計算的濃度與實測濃度較為接近，而后期隨著通風進行，計算風量遠小于實驗風量，炮煙與新鮮空氣之間充分發生擴散作用，因此計算所得濃度要小于實測濃度。由此可知新推導的風量公式與實際通風過程較為接近。

2）由推導公式所計算出來的相同測點位置處的CO濃度值均比實測值要小，而公式計算得到的通風風量遠小于現場實際通風風量，導致計算所得濃度出現較大的下降，這說明風量越大反而并不能起到快速降低炮煙濃度的目的，風量越大巷道風速就越大，因紊流變形作用，CO濃度得以降低。風量較大時，風流速度較大，致使炮煙在排出過程中其濃度還未降到安全允許值時便已經通過了井下作業人員的躲炮位置，這對井下作業人員的安全極為不利；風量較小時，風速較慢，受紊流變形作用和主風流運移作用的共同影響，相同斷面處的CO峰值濃度更低，因此可以證實新推導的風量計算公式更具優勢，可為風機選型提供數據支撐。

4 結 論

1）獨頭巷道壓入式通風過程中，炮煙的排出是紊流變形和擴散稀釋的綜合過程，即隨著巷道長度增加，炮煙帶體積不斷擴大，以及炮煙帶在運移過程中與新鮮風流不斷置換，使巷道中炮煙濃度逐漸降低，從而使炮煙帶濃度達到安全值。

2）在計算炮煙達到安全值所需的風量時，不能把炮煙當成規則控制體來確定通風時間及風量，而要根據實際巷道長度和炮煙生成量來確定。且隨著風量增加，炮煙濃度達到安全值時炮煙帶的運移長度也在相應增加。以炸藥量計算風量的公式所得結果遠大于實際所需風量，會導致炮煙還未降至安全濃度就通過躲炮位置，對作業人員安全造成影響。