細晶壓電涂層/基底界面裂紋熱流強度因子分析

胡帥帥， 劉建生， 李俊林， 魏含玉

(1.太原科技大學材料科學與工程學院， 太原 030024； 2.周口師范學院數學與統計學院， 周口 466000； 3.太原科技大學應用科學學院， 太原 030024)

壓電陶瓷材料由于其出色的性能，在生活和工業中得到了廣泛的應用。材料結構的安全，是保證器件有效穩定工作的前提。目前，受制于制造工藝水平及其他不確定的因素，在材料內部或者界面結合處往往會有缺陷的存在。因此，材料界面缺陷的力學行為的研究尤為必要。近幾十年來，壓電材料的界面裂紋問題吸引了大量的中外學者的廣泛關注[1-5]。Mishra等[6]研究了壓電器件在熱-電-機械加載環境下的多孔洞與裂紋的相互作用。他們利用擴展有限元法、相互作用積分法和廣義Stroh公式預測了應力強度因子，最后借助MATLAB程序對裂紋間的相互作用做了數值模擬。Singh等[7]討論了正交異性復合材料中邊緣裂紋在熱載荷和機械載荷共同作用下的熱應力強度因子。他們借助漸近展開法將積分方程轉化為一對奇異積分方程，得到了集中點載荷作用下邊緣裂紋尖端應力強度因子的解析表達式并計算了在不同裂紋長度和不同導熱率比下應力強度因子的數值，最后通過數值計算分析了兩種不同材料的熱導率比值對熱應力強度因子的影響。王永健等[8]通過復變函數方法分析了壓電雙材料中橢圓孔邊界面裂紋的反平面問題，得出了當橢圓孔退化為豎直裂紋時改變橢圓孔一邊裂紋長度將對另一邊裂紋裂尖場產生很大影響的結論。呂鑫等[9]借助解析函數理論和復變方法分析了一維正方準晶周期方向穿透的拋物線裂紋問題，得出了關于經典彈性理論中的一些新的結果。

以往的壓電材料界面問題研究中，大多都是關于大晶粒壓電材料的研究，而對于細晶粒壓電材料的研究還很少。因此，結合工業的實際需求，對細晶粒壓電涂層的研究就顯得格外重要。基于此，提出了涂層/基底受載荷作用下的界面裂紋問題，在此基礎上構建了細晶粒壓電涂層/基底在熱載荷下作用下的力學模型。借助傅里葉積分手段，推導出了問題的溫度場，確定了熱流強度因子。通過引入數值算例，分析了影響熱流強度因子的相關因素，研究結果對實際工程結構的裂紋診斷具有一定的指導意義。

1 力學模型

如圖1所示，將細晶粒陶瓷粉末通過熱噴涂技術噴涂于壓電基底表面，并將其沿Y軸方向極化形成細晶粒壓電涂層/基底結構。其中，0≤y≤h1為細晶粒壓電涂層，涂層厚度為h1；-h2≤y≤0為壓電基底，基底厚度為h2；-l≤x≤l為Griffith型界面裂紋，裂紋長度為2l，假定裂紋表面處電絕緣、絕熱；Ta、Tb分別為y=h1、y=h2處的環境溫度，假設涂層/基底結構橫觀各向同性。

彈性場、電場的本構方程可以寫為

(1)

(2)

(3)

(4)

(5)

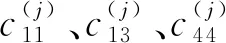
假設溫度場滿足傅里葉熱傳導方程：

(6)

熱邊界連續條件可以寫為

T(x,0+)=T(x,0-), |x|≥l

(7)

T(x,h1)=Ta(x),T(x,h2)=Tb(x), |x|≥0

(8)

(9)

式中：Ta(x)、Tb(x)表示環境溫度；Q0(x)表示對模型所施加的熱流。

2 溫度場

利用積分變換，可以將溫度場的表達式表示為

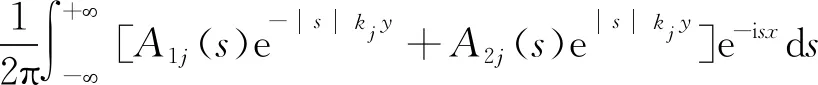
(10)

式(10)中：i為虛數單位；s為引入的變量；A1j(s)、A2j(s)為待定的未知函數，j=1,2。

為了確定溫度場，引入密度函數，其表達式為

(11)

根據邊界連續條件[式(7)]，密度函數G(x)應滿足以下單值條件：

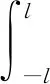
(12)

式(12)中：t為引入的變量。

將式(11)代入熱邊界連續條件式(7)～式(9)，可得

A11(s)+A21(s)-A12(s)-A22(s)=

(13)

(14)

A11(s)e-|s| k1h1+A21(s)e|s| k1h1=

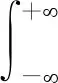
(15)

A12(s)e-|s| k2h2+A22(s)e|s| k2h2=

(16)

式(13)～式(16)可以改寫為

AB=C

(17)

式中：

B=[A11(s),A21(s),A12(s),A22(s)]T；

C=[0,I0,I1,I2]T。

求解式(17)，可得

A11(s)=F1I0-F2I1+F3I2

(18)

A21=F4I1-F5I0-F6I2

(19)

A12(s)=F7I2+F8I0-F9I1

(20)

A22(s)=F10I1-F11I2-F12I0

(21)

式中：

(22)

(23)

(24)

(25)

(26)

(27)

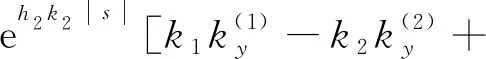
(28)

(29)

(30)

(31)

(32)

(33)

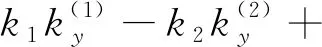
(34)

顯然，只要確定了I0就可以求解出未知函數A1j(s)、A2j(s)，從而就得到了溫度場。

將式(10)代入熱邊界連續條件[式(9)]，可得

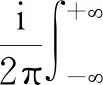
(35)

式(35)中：

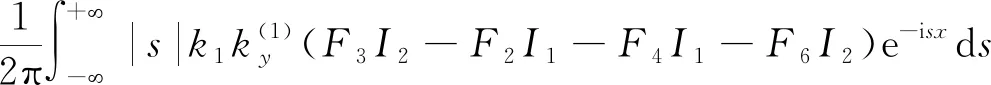
(36)

對式(35)做進一步整理，可得

Q0(x)-d0(x)

(37)

式(37)中：

(38)

式(38)中：M(s)表示關于變量s的函數。

對式(37)改變積分次序，可得

Q0(x)-d0(x)

(39)

式(39)中：

(40)

(41)

式(39)是具有柯西核的奇異積分方程，密度函數G(t)具有平方根奇異性的形式。因此，密度函數G(t)可以表示為

(42)

式(42)中：g0(t)為定義在區間 [-l,l]上的連續函數。

3 熱流強度因子

由文獻[10]可知，熱流強度因子可以定義為

(43)

(44)

式中：L、R分別表示裂紋的左右尖端。

(45)

(46)

將式(42)代入式(45)和式(46)，可得

(47)

(48)

利用切比雪夫多項式配點法，即可求解出g0(-l)和g0(l) 的值。

4 數值計算

為了分析材料參數、裂紋尺寸，涂層厚度對熱流強度因子的影響，接下來選取硒化鎘壓電陶瓷作為基底材料，細晶粒硒化鎘陶瓷作為涂層材料進行數值計算。由文獻[11]可知，通過合適的加工工藝可以使細晶粒壓電材料的壓電、介電性能達到大晶粒壓電材料的壓電、介電水平，而材料的彈性模量有顯著增加。因此，在數值計算中，假設細晶粒硒化鎘陶瓷涂層和普通的硒化鎘壓電陶瓷基底具有相同的壓電、介電常數。

熱流強度因子可以寫為

(49)

(50)

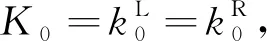
從圖2中可以看出，熱流強度因子隨著涂層厚度的增加而不斷的減小，并逐漸趨于穩定，且涂層與基底彈性模量比值較大者的熱流強度因子具有較高的峰值。這表明，當涂層厚度較厚時對熱流強度因子是不敏感的。由于細晶粒壓電陶瓷材料相較于同種大晶粒壓電陶瓷材料可以把基片做得更薄，且具有更高的彈性模量，因此細晶粒壓電陶瓷材料具有更廣泛的工程意義。圖3給出了熱流強度因子隨裂紋長度發生變化的規律。

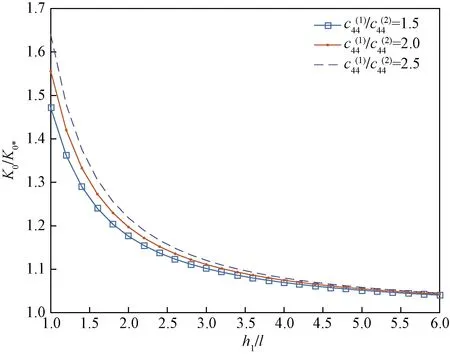
圖2 熱流強度因子與涂層厚度之間的關系Fig.2 Relationship between thermal strength factor and coating thickness

從圖3中可以看出，當涂層厚度較小時，熱流強度因子隨著裂紋長度的增加而增加。這表明，當細晶粒壓電涂層/基底結構受到一定強度的熱載荷時，會造成裂紋的擴展，結構的損壞。

圖3 熱流強度因子與裂紋尺寸之間的關系Fig.3 Relationship between thermal strength factor and crack size

5 結論

利用傅里葉積分變換方法，構造出了含Griffith型界面裂紋的細晶粒壓電涂層/基底在熱載荷作用下的溫度場的表達式，推導出了熱流強度因子的具體形式，得出如下結論。

(1)驗證了涂層/基底為同一種材料時的特殊情況，得出了與以往文獻相同的結論。

(2)通過數值算例分析了熱流強度因子與細晶粒壓電涂層的厚度及裂紋尺寸之間的關系，涂層厚度較薄時，對熱流強度因子比較敏感，隨著涂層厚度增加，熱流強度因子逐漸趨于穩定。