煤巖力學非均質性對孔滲性質的影響規律

劉雄飛， 郭建設， 汪道兵， 董永存， 李秀輝， 宇 波

(1.中國石油大學(北京)非常規油氣科學技術研究院， 北京 102249; 2.東北石油大學石油工程學院， 大慶 163318； 3.中國石油吐哈油田分公司， 哈密 838202； 4.北京石油化工學院機械工程學院， 北京 102617； 5.北京石油化工學院， 深水油氣管線關鍵技術與裝備北京市重點實驗室， 北京 102617)

煤巖是由有機物質和無機礦物質混合組成的復雜不均勻介質，具有很強的非均質性[1-2]。煤層氣開采時滲透率和孔隙度受溫度場、流動壓力和巖石變形三者共同影響作用，地下煤巖的滲透率和孔隙度變化過程本質上為非均質巖體內熱流固耦合過程[3-4]。CT掃描實驗表明煤巖內部發育大量割理與裂隙[1,5-8]，此特征使得煤巖存在強宏觀力學非均質性，因此傳統的均勻連續性假設與地下真實情況不相符，建立在傳統均質假設基礎上的孔隙度與滲透率時空演化分析方法受到嚴重挑戰，這成為目前煤層氣開采過程中亟待解決的關鍵力學問題。

煤層氣開采過程中，受甲烷熱傳導、解吸和吸附的綜合作用，煤巖溫度發生變化[9-12]。實驗證明，甲烷解吸過程中煤巖溫度下降5 ℃左右[5-10]。因此，溫度引起的熱應力作用使得煤巖變形，從而將影響煤巖滲透率和孔隙度變化。在數值模擬方面，楊天鴻等[12]建立了考慮甲烷氣體解吸、吸附作用的氣體滲流—應力耦合作用模型，模擬結果表明：圍壓對瓦斯抽放效果影響較大，高圍壓下，若沒有卸壓作用，滲流阻力較大，瓦斯開采效果較差，但是該模型未考慮溫度效應對煤巖滲透性的影響。侯永強等[6]建立了高溫高壓井筒耦合傳熱數學模型，應用有限差分法對該數學模型進行求解，通過數值模擬，得到了井筒及其腔體內流體的耦合傳熱過程溫度場變化規律，該模型可為模擬井筒加溫過程提供理論依據。王俊等[8]通過多場耦合數值模擬，分別研究泄漏壓力、環境溫度和障礙物等因素對埋地管道泄漏擴散的影響規律，結果表明，甲烷濃度隨時間的變化曲線主要分為3個階段：孕育階段、快速增長階段和緩慢增長階段。馬忠[13]考慮了瓦斯抽采期間的溫度效應，建立了煤巖熱流固耦合模型，結果表明提高溫度可以促進大量吸附的瓦斯解吸，同時解析作用使得煤巖變形，有利于增加煤巖滲透率和孔隙度，但是該模型未考慮煤巖力學非均質性對煤巖孔滲參數的影響。在熱流固模型基礎上，魏晨慧[10]建立了熱流固損傷耦合模型，研究了不同側壓系數和孔壁增溫條件下煤巖的地應力變化和損傷演化過程，但是本模型為二維模擬。室內實驗研究表明，煤巖滲透率與圍壓、溫度和氣壓密切相關，煤巖滲透率一般隨溫度的升高呈遞減趨勢，但也有呈現先減小后增大趨勢可能，因為煤巖滲透率變化是熱膨脹、解吸和裂隙殘余水分蒸發三者耦合作用結果[1-4]。但是，煤巖孔滲測試實驗結果存在著較強的尺寸效應，即煤巖試樣樣品尺寸不同，孔滲測試實驗結果也不同。

基于Weibull隨機分布函數表征煤巖力學非均質性，建立了考慮煤巖甲烷吸附、解吸、煤巖變形、溫度效應和氣體壓力相互耦合的滲透率與孔隙度時空演化三維有限元模型，通過Petrov-Galerkin有限元離散，分析了非均質度煤巖井筒附近孔滲參數的變化規律。研究結果對指導煤層氣高效開采具有重要理論意義。

1 控制方程

研究涉及3個物理過程，即煤巖變形、甲烷氣體滲流和傳熱過程，這3個過程之間是相互耦合的。各物理場控制方程如下。

1.1 巖石應力平衡方程

根據彈性力學理論，煤巖變形時滿足的力學平衡方程為[11]

σij,j+Fi=0

(1)

式(1)中：σij為總應力張量， MPa；σij,j表示σij對第j個分量的偏導數；Fi為體積力向量， MPa。

根據Terzaghi有效應力理論，總應力場可分解為巖石骨架承受的有效應力場和孔隙內流體壓力場，即

σij,j=σ′ij,j+αPδij

(2)

式(2)中：σ′ij為有效應力張量， MPa；σ′ij，j表示σ′ij對第j個分量的偏導數， MPa；α為Biot孔隙彈性常數，取值為0～1的小數；P為孔隙壓力， MPa；δij為Kronecker符號。

煤巖變形時的總應變除了彈性應變外，還包括甲烷氣體壓力引起的應變、煤巖顆粒吸附甲烷所引起的線性吸附膨脹應變和熱膨脹應變。因此，有效應力張量可表達為[12]

(3)

式(3)中：λ、G為拉梅常數， MPa；εv為巖石體積應變，小數；β為熱膨脹系數， K-1；a、b為Langmuir吸附常數，單位分別為m3/kg和 MPa-1；Ks為煤巖顆粒體積模量， MPa；Vm為氣體摩爾體積，L/mol；ρ為煤巖密度，kg/m3；T為溫度，K；R為摩爾氣體常數，J/(mol·K)；Δ為拉普拉斯算子；εij為應變張量。

煤巖變形時幾何方程為[3,13-16]

(4)

式(4)中：u為巖石位移向量，m。

聯立式(1)～式(4)可得煤巖變形的力學平衡方程為[12-18]

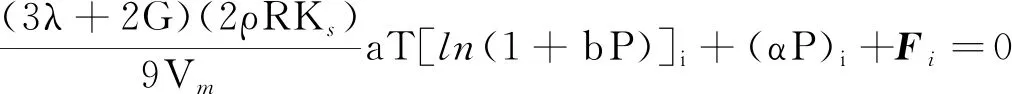
(5)

式(5)中：γ為泊松比；Pi為對壓力x、y、z方向的偏導數。

1.2 滲流場控制方程

根據質量守恒定律、達西定律和Langmuir吸附方程，可得煤巖內甲烷氣體滿足的滲流場方程為[4,6,15-19]

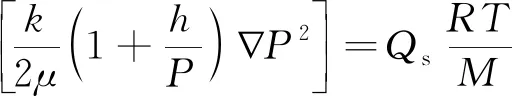
(6)

式(6)中：φ為煤巖孔隙度；t為時間，s；k為煤巖滲透率，m2；μ為氣體黏度，mPa·s；M為氣體分子量，g/mol；h為Klinkenberg系數，Pa；c為校正系數，kg/m3；Qs為源匯項，kg/(m3·s)。

1.3 溫度場控制方程

根據傅里葉定律和能量守恒方程，可得溫度場控制方程為[9-11]

(7)

式(7)中：η為煤巖導熱系數，W/(m·K)；Cv為定容比熱容，J/(kg·K)；Q為甲烷含量，t/m3；q為氣體滲流速度，m/s；T0為參考溫度，K。

1.4 交叉耦合方程

在熱流固耦合過程中，煤巖的孔隙度和滲透率為氣體壓力、溫度場和巖石變形(或應力場)的函數，其表達式為[3,12,17-20]

(8)

(9)

式中：φ0為初始孔隙度；k0為初始滲透率，m2。式(8)、式(9)體現了煤層氣吸附、解吸、壓縮、溫度-滲流-應力耦合影響作用下巖石滲透率和孔隙度的不用機制，體現了熱流固耦合作用下煤巖孔滲演化規律。

2 計算模型和方案

2.1 模型簡介

由于三維熱流固耦合問題計算量巨大，為節省計算成本，選取邊長為1 m×1 m×1 m的表征單元體(representation elementary volume, RVE)作為物理模型，RVE中間含有半徑為0.2 m的鉆井井眼。采用四面體單元對RVE進行三維網格劃分，共計有34 878個四面體單元；為準確模擬井周的應力集中現象，在井眼附近進行局部網格加密處理，如圖1所示。此外，時間導數離散項采用隱式格式，自適應時間步長，并采用Petrov-Galerkin有限元格式，可以確保熱流固耦合模型的計算穩定性[17-24]。

圖1 三維網格剖分示意圖Fig.1 Diagram of three-dimensional mesh generation

邊界條件定義如下：①固體力學模塊：對表征單元體RVE的六個面采用Roller邊界條件，井筒采用自由邊界條件；②流動壓力模塊：對表征單元體RVE六個面采用恒流量邊界條件，井筒采用恒壓邊界條件；③熱傳導模塊：對表征單元體RVE所有邊界采用絕熱邊界條件。

2.2 非均質性表征

Weibull分布是描述巖石非均質性的一種有效方法[10,20]，具體計算時使得巖石的某些物理參數服從Weibull分布，這些物理參數的隨機賦值通過Monte Carlo法實現，從而實現對巖石非均質性的描述。Weibull的概率密度函數表達式為[3]

(10)

式(10)中：x為隨機變量，可取彈性模量、滲透率等物理參數；m為形狀參數，表示非均質程度大小，m值越小，巖石非均質性越強；n為隨機變量參數的平均值。

如圖2所示，考慮煤巖彈性模量的隨機分布，圖2(a)、圖2(b)分別為表征單元體內彈性模量的三維分布云圖和不同平面處的切面云圖，m=7，彈性模量平均值n=1.85 GPa。

圖2 煤巖三維力學非均質性表征Fig.2 Three-dimensional mechanical heterogeneity characterization of coal rock

2.3 數值模擬參數及方案

有限元模型的輸入參數如表1所示，分別模擬均質地層、非均質參數m=7時的熱流固耦合過程，獲得應力場、溫度場和壓力場的三維分布，并分析不同條件下井周孔隙度、滲透率隨時間、距離井眼距離的變化規律。

表1 模型輸入參數

3 模擬結果

3.1 均質性煤巖的數值模擬結果

在均質彈性模量情況下，不同時刻煤巖滲透率與孔隙度隨井眼距離的變化曲線如圖3所示，可以看出，隨開采時間增加，煤巖井筒附近的滲透率與孔隙度呈現下降趨勢，開采前期，下降速度較快；當開采時間達到106s后下降速度減慢；隨著井眼距離的增加，煤巖井筒附近的滲透率與孔隙度也呈現下降趨勢，在距離井眼0.2 m以內區域，下降幅度較小，而在距離井眼0.2 m以外地方，滲透率與孔隙度下降速度較快。

圖3 不同時刻煤巖孔隙度與滲透率隨井眼距離的變化曲線Fig.3 The variation curve of coal porosity and permeability with borehole distance at different time

煤巖表征單元體的三維位移場、孔隙壓力場和溫度場分布云圖如圖4～圖6所示。從位移場云圖可以看出，井筒附近位移場數值較大，說明井筒周圍發生了應力集中現象，應力集中區域隨著開采時間增加也逐漸向井筒外圍波及；從壓力場云圖上看，井周孔隙壓力場呈現圓形分布特征，隨著開采時間增加，壓力波逐漸向井筒外波及；從溫度場云圖上看，隨著開采時間增加，井筒附近溫度也逐漸降低，這是由于甲烷的吸附、解吸作用引起的，并且隨著開采時間增加，溫度場波及區域也逐漸向外擴大。

圖4 不同時刻煤巖位移場x分量的三維云圖Fig.4 Three-dimensional contour of x component of coal displacement field at different time

圖5 不同時刻煤巖孔隙壓力場的三維云圖Fig.5 Three-dimensional contour of coal pore pressure field at different time

圖6 不同時刻煤巖溫度場的三維云圖Fig.6 Three-dimensional contour of coal temperature field at different time

3.2 非均質性煤巖的數值模擬結果

在非均質彈性模量情況下，不同時刻煤巖滲透率與孔隙度隨井眼距離的變化曲線如圖7所示，可看出，與均質情況相比，非均質地層的滲透率與孔隙度分布呈現出波動震蕩分布特征，距離井眼不同位置處的孔滲參數大小不一；隨著時間增加，煤巖滲透率和孔隙度也呈現遞減趨勢；然而，在同一時刻，隨著井眼距離增加，滲透率和孔隙度整體呈現增加趨勢，與均質煤巖情況恰好相反，這是由于力學非均質性引起的。

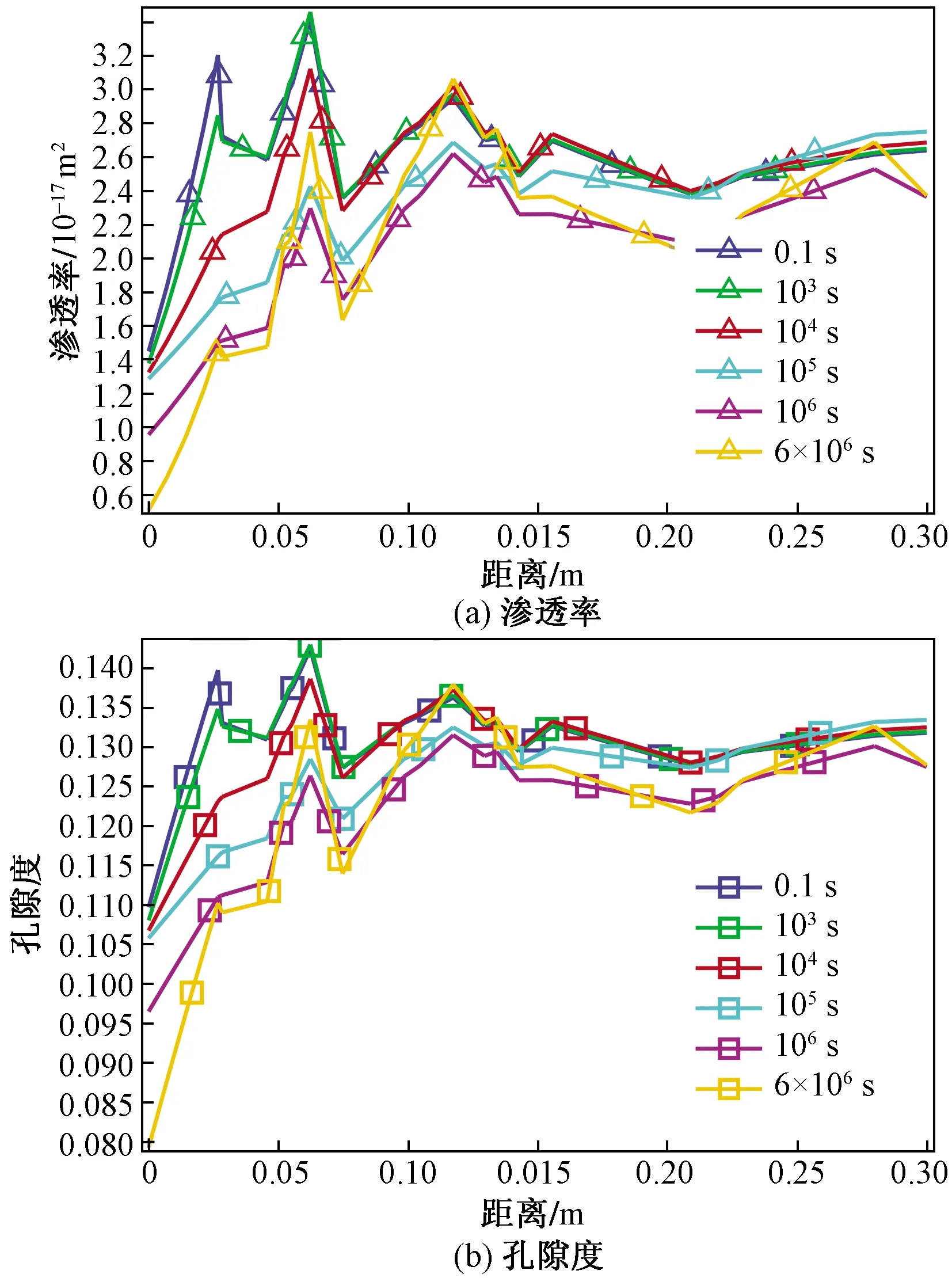
圖7 不同時刻煤巖孔隙度與滲透率隨井眼距離的變化曲線Fig.7 The variation curve of coal porosity and permeability with borehole distance at different time

煤巖表征單元體的應力場、孔隙壓力場和溫度場的二維切片分布云圖如圖8～圖10所示。從應力場云圖上看，井周的應力場分量Sxx呈現出隨機分布特征，隨著開采時間增加，傳播區域逐漸向井筒外圍擴張；從壓力場云圖上看，井周孔隙壓力場呈現圓形分布特征，隨著開采時間增加，壓力波逐漸向井筒外波及，與均質情況類似；從溫度場云圖上看，在開采時間初期，井筒附近溫度也呈現了隨機分布特征；當時間達到103s以后，溫度分布基本均勻；隨著時間延長，溫度場分布也逐漸向井筒外圍傳播。

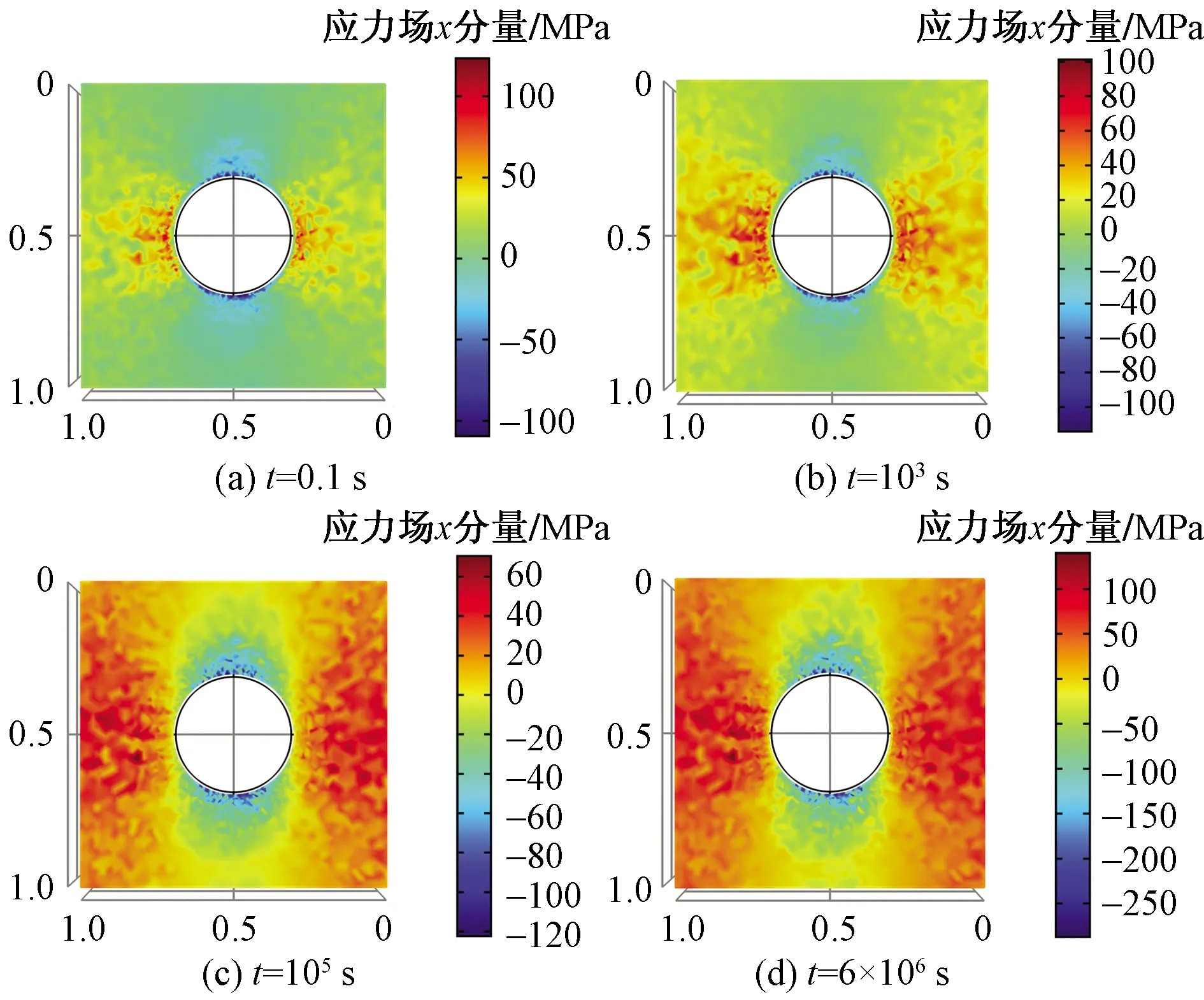
圖8 不同時刻煤巖應力分量Sxx的二維切片云圖Fig.8 Two-dimensional slice of x component of coal stress field at different time

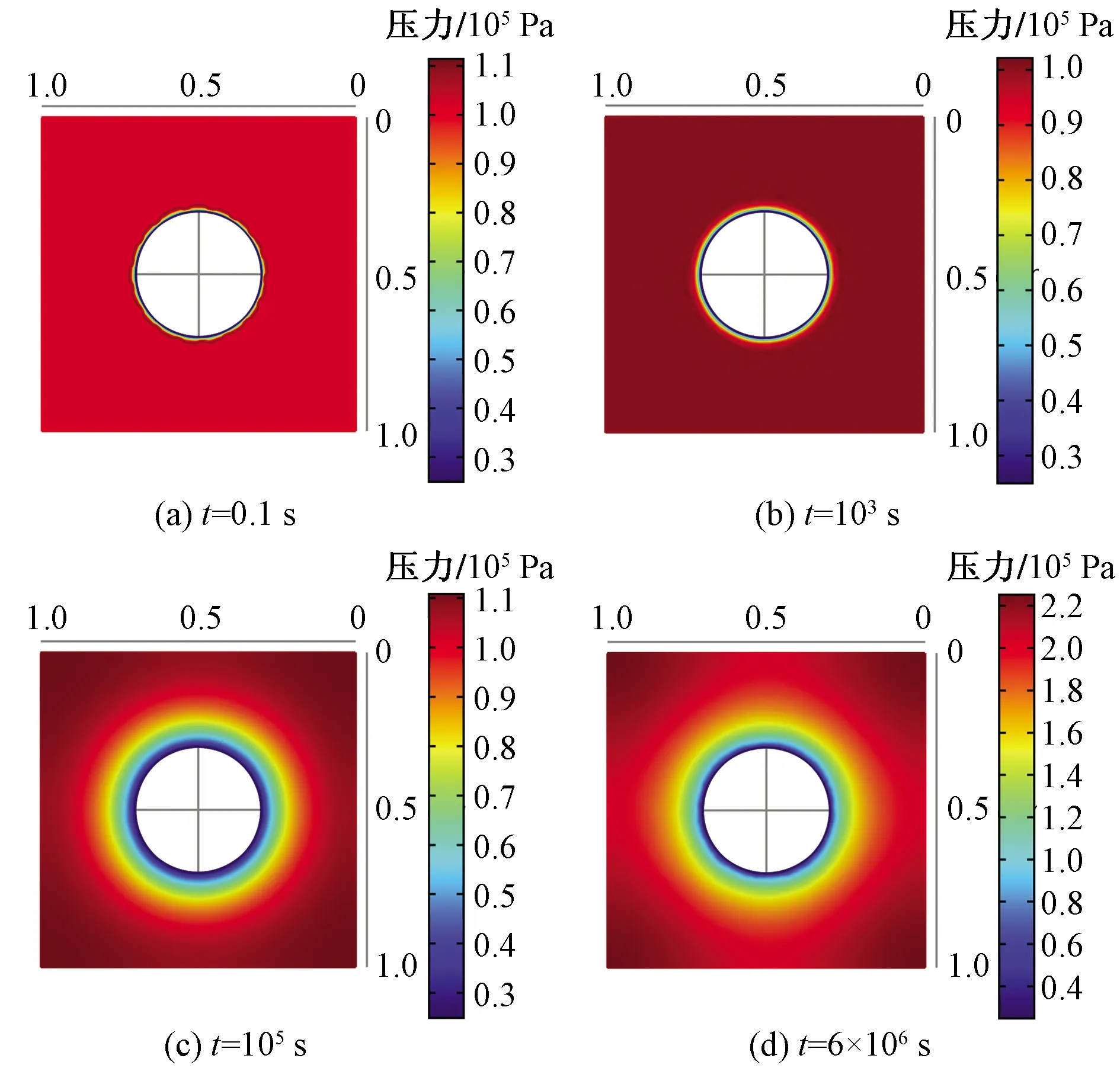
圖9 不同時刻煤巖孔隙壓力場的二維切片云圖Fig.9 Two-dimensional slice of coal pore pressure field at different time

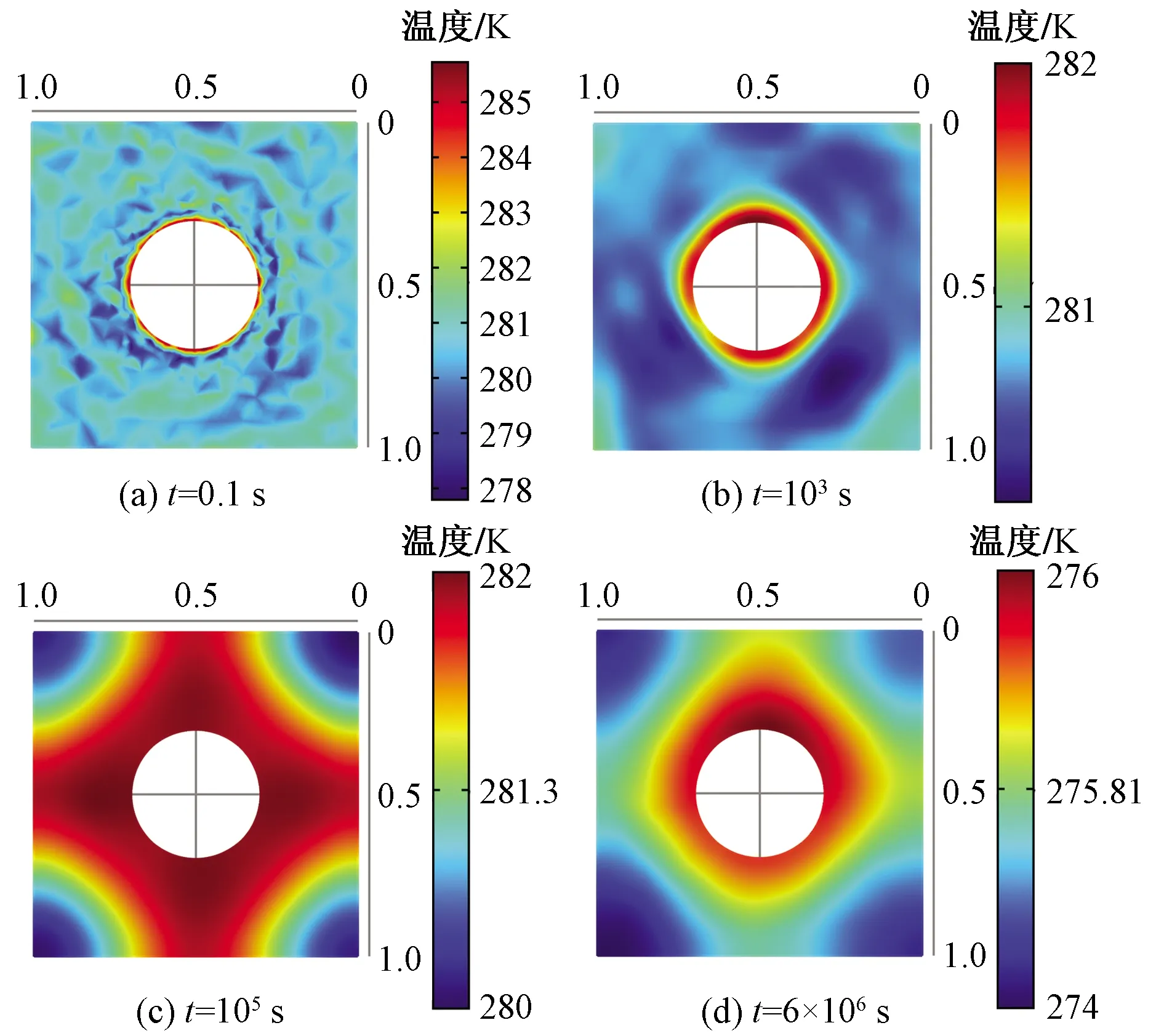
圖10 不同時刻煤巖溫度場的二維切片云圖Fig.10 Two-dimensional slice of coal temperature field at different time

4 結論

基于Weibull隨機分布函數表征煤巖力學非均質性，建立了考慮煤巖內甲烷氣體解吸、吸附引起的壓力變化、巖石變形和熱膨脹效應的熱流固耦合三維有限元模型，通過煤巖滲透率、孔隙度與熱流固耦合效應間的關聯式，數值模擬了煤巖滲透率、孔隙度的時空演化規律，得出如下主要結論。

(1)煤巖力學非均質性對煤巖滲透率與孔隙度影響顯著，與均質煤巖相比，非均質地層的滲透率與孔隙度分布呈現出波動震蕩分布特征，距離井眼不同位置處的孔滲參數大小不一。

(2)非均質煤巖滲透率和孔隙度隨著開采時間增加呈現遞減趨勢；隨著井眼距離增加，滲透率和孔隙度整體呈現增加趨勢，這與均質煤巖情況恰好相反，這是由于力學非均質性引起的。

(3)非均質煤巖的孔隙度與滲透率演化是一個復雜的熱流固耦合過程，與力學非均質性、熱膨脹效應、甲烷氣體解吸引起的壓力變化和煤巖骨架的應力變形密切相關。