利用增廣雅克比矩陣的冗余機(jī)械臂逆運(yùn)動(dòng)學(xué)求解算法

王 騰， 張承瑞*， 陳齊志， 薛祥儒

(1.山東大學(xué)機(jī)械工程學(xué)院， 濟(jì)南 250061； 2.山東大學(xué)， 高效潔凈機(jī)械制造教育部重點(diǎn)實(shí)驗(yàn)室， 濟(jì)南 250061)

當(dāng)機(jī)械臂自身所具有的自由度多于執(zhí)行給定任務(wù)所需的自由度時(shí)，機(jī)械臂存在運(yùn)動(dòng)學(xué)冗余。相比于非冗余機(jī)械臂，運(yùn)動(dòng)學(xué)冗余使得機(jī)械臂具備了更高的靈活性。

一般來說，運(yùn)動(dòng)學(xué)逆解分為封閉解[1-2]和數(shù)值解兩種形式。封閉解具有很高的計(jì)算效率，這使其在實(shí)時(shí)控制中受到青睞。文獻(xiàn)[3]在獲得的與臂型角相關(guān)的解析表達(dá)式的基礎(chǔ)上，通過優(yōu)化最小勢(shì)能指標(biāo)確定臂型角的大小，然后對(duì)各關(guān)節(jié)位置進(jìn)行了求解。文獻(xiàn)[4]通過限制臂型角的范圍，使得逆解結(jié)果不會(huì)導(dǎo)致機(jī)械臂發(fā)生自身碰撞。文獻(xiàn)[5]對(duì)機(jī)械臂的構(gòu)型進(jìn)行了分析，并根據(jù)幾何特性獲得了多關(guān)節(jié)偏置機(jī)械臂的封閉解。然而封閉形式的運(yùn)動(dòng)學(xué)逆解只適用于特定結(jié)構(gòu)的機(jī)械臂，通用性較差。數(shù)值計(jì)算方法不尋求一種解析關(guān)系[6-7]，因此適用于大多數(shù)的機(jī)械臂。為了滿足實(shí)時(shí)控制需求，在實(shí)際應(yīng)用中需要考慮數(shù)值逆解算法的求解效率。

梯度投影法(gradient projection method，GPM)[8]利用機(jī)械臂在雅可比矩陣零空間的“自運(yùn)動(dòng)”解決冗余問題。文獻(xiàn)[9]在此基礎(chǔ)上選用阻尼最小二乘形式的偽逆，使機(jī)械臂具備了避開奇異位姿的能力。文獻(xiàn)[10]將阻尼最小二乘偽逆求解方法與牛頓-拉夫遜迭代方法相結(jié)合，提高了軌跡跟蹤精度。文獻(xiàn)[11]利用由碰撞檢測(cè)反饋的避障向量構(gòu)造目標(biāo)函數(shù)，實(shí)現(xiàn)了機(jī)械臂在復(fù)雜場(chǎng)景下的避障。然而，工作空間中的封閉路徑通過偽逆方法映射到關(guān)節(jié)空間后卻不是封閉的，即執(zhí)行循環(huán)任務(wù)時(shí)，機(jī)械臂并不能回到初始位姿，這使得機(jī)械臂的運(yùn)動(dòng)不可預(yù)測(cè)[12]。運(yùn)動(dòng)的不可重復(fù)性限制了冗余機(jī)械臂的應(yīng)用范圍。文獻(xiàn)[13]將機(jī)械臂的子任務(wù)選擇為優(yōu)化保證可重復(fù)運(yùn)動(dòng)的目標(biāo)函數(shù)，使機(jī)械臂的運(yùn)動(dòng)具備可重復(fù)性。但是將運(yùn)動(dòng)學(xué)冗余用于獲得非冗余機(jī)械臂的基本特性，并沒有發(fā)揮出冗余機(jī)械臂應(yīng)有的優(yōu)勢(shì)。雖然通過加權(quán)可以使目標(biāo)函數(shù)結(jié)合多種優(yōu)化準(zhǔn)則，但由于優(yōu)化能力有限，任務(wù)的執(zhí)行效果會(huì)受到影響。

增廣雅克比矩陣方法通過添加作為額外約束的優(yōu)化任務(wù)，對(duì)原始任務(wù)進(jìn)行增廣以解決冗余[14]。該方法能夠保證機(jī)械臂運(yùn)動(dòng)的可重復(fù)性，但隨著機(jī)械臂關(guān)節(jié)數(shù)目的增多，約束條件的計(jì)算難度增大。為解決增廣雅可比矩陣方法中約束計(jì)算復(fù)雜的問題，提出了一種冗余機(jī)械臂逆運(yùn)動(dòng)學(xué)求解算法。該算法采用分解求解策略，實(shí)現(xiàn)對(duì)復(fù)雜的約束條件的計(jì)算，求解效率高，可實(shí)際應(yīng)用于七自由度冗余機(jī)械臂的實(shí)時(shí)控制。現(xiàn)以避關(guān)節(jié)極限準(zhǔn)則作為約束條件增廣雅可比矩陣，采用提出的分解計(jì)算策略對(duì)約束條件進(jìn)行分解，計(jì)算獲得增廣部分的數(shù)值結(jié)果，在笛卡爾空間進(jìn)行軌跡規(guī)劃后，利用增廣雅可比矩陣計(jì)算出關(guān)節(jié)速度，對(duì)關(guān)節(jié)速度積分得到關(guān)節(jié)位置，完成逆運(yùn)動(dòng)學(xué)的求解。

1 運(yùn)動(dòng)學(xué)冗余求解方法

對(duì)于具有n個(gè)關(guān)節(jié)的機(jī)械臂，定義qi(i=1,2,…,n)表示第i個(gè)關(guān)節(jié)的位置，則機(jī)械臂的位姿可由向量q=[q1,q2,…,qn]T唯一確定。維度為m的向量x表示機(jī)械臂末端相對(duì)于基坐標(biāo)的位置與姿態(tài)。當(dāng)n>m時(shí)，對(duì)于給定的任務(wù)來說，機(jī)械臂是運(yùn)動(dòng)學(xué)冗余的，冗余自由度r=n-m。關(guān)節(jié)空間與笛卡爾空間之間的關(guān)系由正運(yùn)動(dòng)學(xué)公式表示為

x=f(q)

(1)

式(1)中：f為與關(guān)節(jié)位置和機(jī)械臂連桿參數(shù)有關(guān)的非線性向量函數(shù),f:Rn→Rm。

對(duì)時(shí)間求導(dǎo)，得到速度層面的運(yùn)動(dòng)學(xué)關(guān)系為

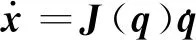
(2)

1.1 梯度投影法

微分運(yùn)動(dòng)學(xué)的最小范數(shù)解為

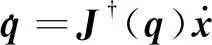
(3)

式(3)中：J?=JT(JJT)-1為雅克比矩陣J的Moore-Penrose偽逆。在式(3)的基礎(chǔ)上增加一個(gè)齊次項(xiàng)，則微分運(yùn)動(dòng)學(xué)的通解可以表示為

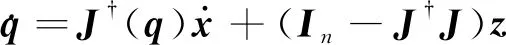
(4)

式(4)中：In為n×n的單位陣；z為n維的任意向量；In-J?J為J的零空間的投影算子。式(4)使得冗余機(jī)械臂具備在跟蹤目標(biāo)軌跡的過程中，利用“自運(yùn)動(dòng)”執(zhí)行與優(yōu)化準(zhǔn)則相關(guān)的子任務(wù)的能力。

令H(q)為選定的目標(biāo)函數(shù)，要最小化H(q)，那么z可以表示為

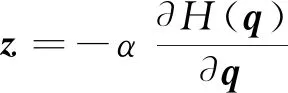
(5)

式(5)中：α為標(biāo)量正實(shí)數(shù)，其數(shù)值的大小影響優(yōu)化的收斂速率。

1.2 增廣雅可比矩陣方法

引入跟蹤軌跡之外的任務(wù)擴(kuò)展任務(wù)空間，則機(jī)械臂在運(yùn)動(dòng)過程中會(huì)受到額外任務(wù)的約束。將機(jī)械臂的額外任務(wù)選擇為在運(yùn)動(dòng)中滿足給定的準(zhǔn)則，那么機(jī)械臂的運(yùn)動(dòng)也可以看作是在運(yùn)動(dòng)學(xué)公式的約束下優(yōu)化相關(guān)的目標(biāo)函數(shù)H(q)。優(yōu)化問題可以表示為

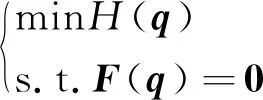
(6)

式(6)中：F(q)=f(q)-x由運(yùn)動(dòng)學(xué)公式獲得，表示運(yùn)動(dòng)學(xué)約束函數(shù)。

當(dāng)目標(biāo)函數(shù)H(q)取極值時(shí)，H(q)的梯度在雅克比矩陣零空間上的投影為零[14]。假定q0為使目標(biāo)函數(shù)局部最優(yōu)的非奇異位姿，那么存在的關(guān)系為

(7)

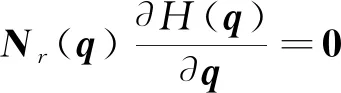
(8)

式(8)中：Nr為由In-J?J中線性獨(dú)立的行所組成的r×n的矩陣。

將式(8)作為運(yùn)動(dòng)學(xué)公式的額外約束，那么機(jī)械臂運(yùn)動(dòng)過程中所要遵循的條件可表示為

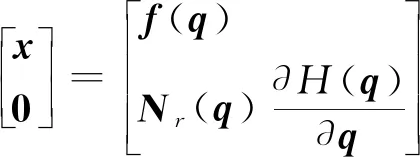
(9)

對(duì)式(9)兩側(cè)求導(dǎo)，能夠獲得增廣后的微分運(yùn)動(dòng)學(xué)公式為

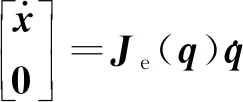
(10)

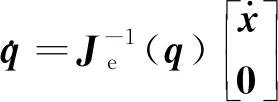
(11)

對(duì)于工作空間中任意給定的點(diǎn)，求解式(11)能獲得唯一相對(duì)應(yīng)的位姿，這是機(jī)械臂運(yùn)動(dòng)具備可重復(fù)性的表現(xiàn)。

2 冗余機(jī)械臂逆運(yùn)動(dòng)學(xué)求解算法

利用增廣雅可比矩陣方法求解逆運(yùn)動(dòng)學(xué)問題，關(guān)鍵是雅可比矩陣增廣部分的計(jì)算。本文算法從增廣部分的形式和計(jì)算方法兩方面入手，解決機(jī)械臂關(guān)節(jié)數(shù)目較多時(shí)，增廣部分計(jì)算復(fù)雜的問題。

2.1 增廣部分推導(dǎo)

式(6)所表示的優(yōu)化問題可使用拉格朗日乘子法求解[15]。通過構(gòu)建拉格朗日函數(shù)，可以將帶約束的優(yōu)化問題轉(zhuǎn)換為無約束的形式。定義拉格朗日函數(shù)為

L(q,λ)=H(q)+λTF(q)

(12)

式(12)中：λ為m維的拉格朗日乘子向量。

拉格朗日函數(shù)取極值時(shí)滿足：

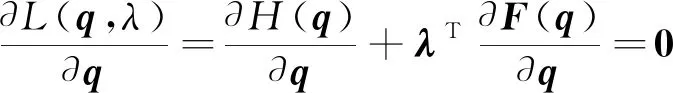
(13)

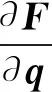
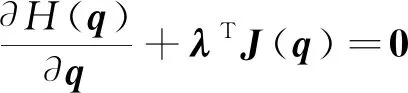
(14)

根據(jù)式(14)，文獻(xiàn)[15]推導(dǎo)出額外約束公式，可表示為

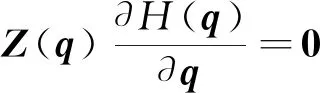
(15)

定義Ji(i=1,2,…,n)為J的第i列。式(15)中，投影算子Z為(n-m)×n的矩陣，它由J的零空間的n-m個(gè)線性獨(dú)立的行向量組成，其表達(dá)式為

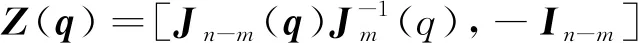
(16)

式(15)形式下的額外約束的導(dǎo)數(shù)矩陣Ca為

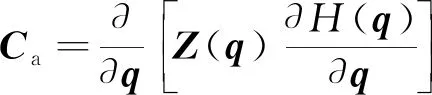
(17)

對(duì)比式(15)與式(16)中投影算子的形式可以看出，由于涉及雅可比矩陣的偽逆J?，使得Nr計(jì)算復(fù)雜。由式(16)可以看出，Z的計(jì)算主要與雅可比矩陣的列有關(guān)，利用矢量積方法[16]得出雅可比矩陣后，很容易便能確定所需的列向量。更重要的是，矩陣的逆運(yùn)算僅涉及形式簡單的單個(gè)矩陣，與J?相比，計(jì)算量大幅減小。為構(gòu)造增廣雅可比矩陣，需要將額外約束相對(duì)于關(guān)節(jié)位置向量的偏導(dǎo)數(shù)作為矩陣的增廣部分。然而，對(duì)于實(shí)際使用的七自由度冗余機(jī)械臂來說，計(jì)算Z已經(jīng)足夠復(fù)雜，對(duì)矩陣的增廣部分的計(jì)算就變得更加困難。

2.2 增廣部分分解計(jì)算

為計(jì)算Ca的數(shù)值結(jié)果，對(duì)式(17)做進(jìn)一步分解。當(dāng)n-m=1時(shí)，Ca可以表示為

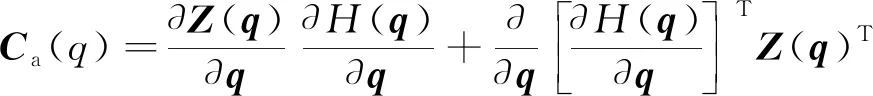
(18)

為了進(jìn)一步減少計(jì)算量，應(yīng)盡可能地避免對(duì)目標(biāo)函數(shù)進(jìn)行兩次求導(dǎo)運(yùn)算。實(shí)際上，一個(gè)簡單且有效的目標(biāo)函數(shù)能夠提供顯式的導(dǎo)數(shù)表達(dá)式，這樣二階導(dǎo)數(shù)值可以僅通過對(duì)顯式的導(dǎo)數(shù)表達(dá)式進(jìn)行一次求導(dǎo)而獲得。避關(guān)節(jié)極限準(zhǔn)則[17]可以選作目標(biāo)函數(shù)，其定義為

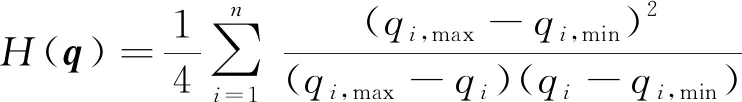
(19)

式(19)中：qi,min和qi,max分別為第i個(gè)關(guān)節(jié)的位置qi的上限和下限。

2.3 算法流程

求解冗余逆運(yùn)動(dòng)學(xué)問題的算法流程如下。

Step 1利用矢量積方法計(jì)算雅可比矩陣J。

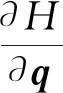
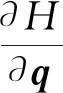
Step 4利用Ca對(duì)J增廣，構(gòu)造增廣雅可比矩陣Je。

Step 5計(jì)算Je的逆矩陣。

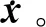
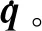
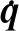
3 仿真及實(shí)驗(yàn)驗(yàn)證

為驗(yàn)證本文方法的有效性，首先通過仿真與梯度投影法進(jìn)行對(duì)比，然后將其應(yīng)用于如圖1所示的7自由度(degree of freedom, DOF)冗余機(jī)械臂的實(shí)時(shí)控制。機(jī)械臂的MDH(modified Denavit-Hartenberg)參數(shù)如表1所示。選用式(19)作為兩種方法中被優(yōu)化的目標(biāo)函數(shù)，以避免運(yùn)動(dòng)過程中機(jī)械臂關(guān)節(jié)位置超出限位。機(jī)械臂各關(guān)節(jié)的運(yùn)動(dòng)范圍如表2所示。

圖1 7自由度冗余機(jī)械臂Fig.1 7-DOF redundant manipulator

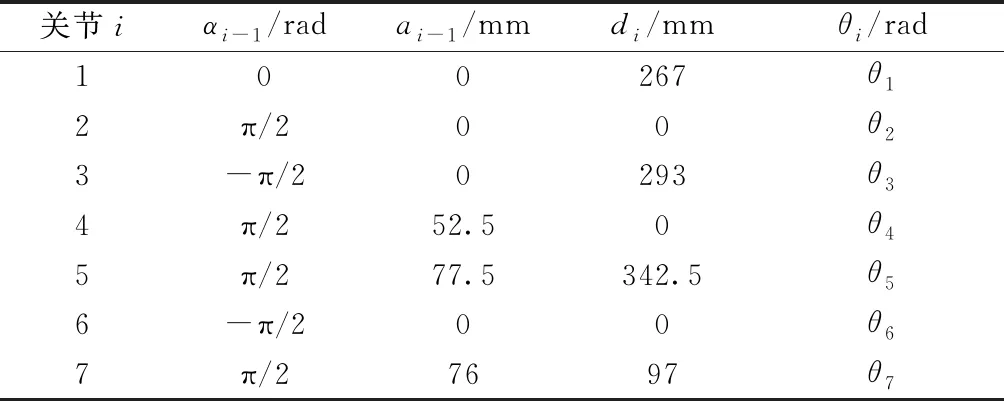
表1 機(jī)械臂MDH參數(shù)

表2 機(jī)械臂關(guān)節(jié)運(yùn)動(dòng)范圍

3.1 仿真對(duì)比

為評(píng)估本文算法的性能表現(xiàn)，使機(jī)械臂末端姿態(tài)保持不變，從A點(diǎn)開始，按逆時(shí)針方向，沿如圖2所示的空間四邊形封閉路徑運(yùn)動(dòng)。機(jī)械臂的初始位姿q=[-10°,-20°,0°,65°,10°,-50°,35°]T。四邊形路徑的頂點(diǎn)分別為A(507.02,-84.91,234.01)、B(507.02,75.09,234.01)、C(487.02,75.09,394.01)、D(487.02,-84.91,394.01)。該路徑分為AB、BC、CD、DA四段，每段分別使用S曲線[18]進(jìn)行加減速規(guī)劃，規(guī)劃后機(jī)械臂末端的位置、速度變化曲線分別如圖3、圖4所示。

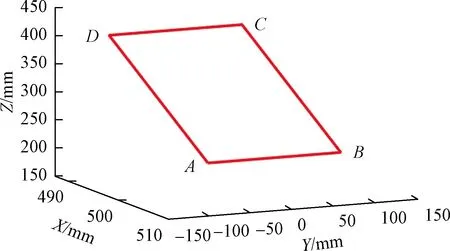
圖2 笛卡爾空間封閉路徑Fig.2 Closed path in Cartesian space

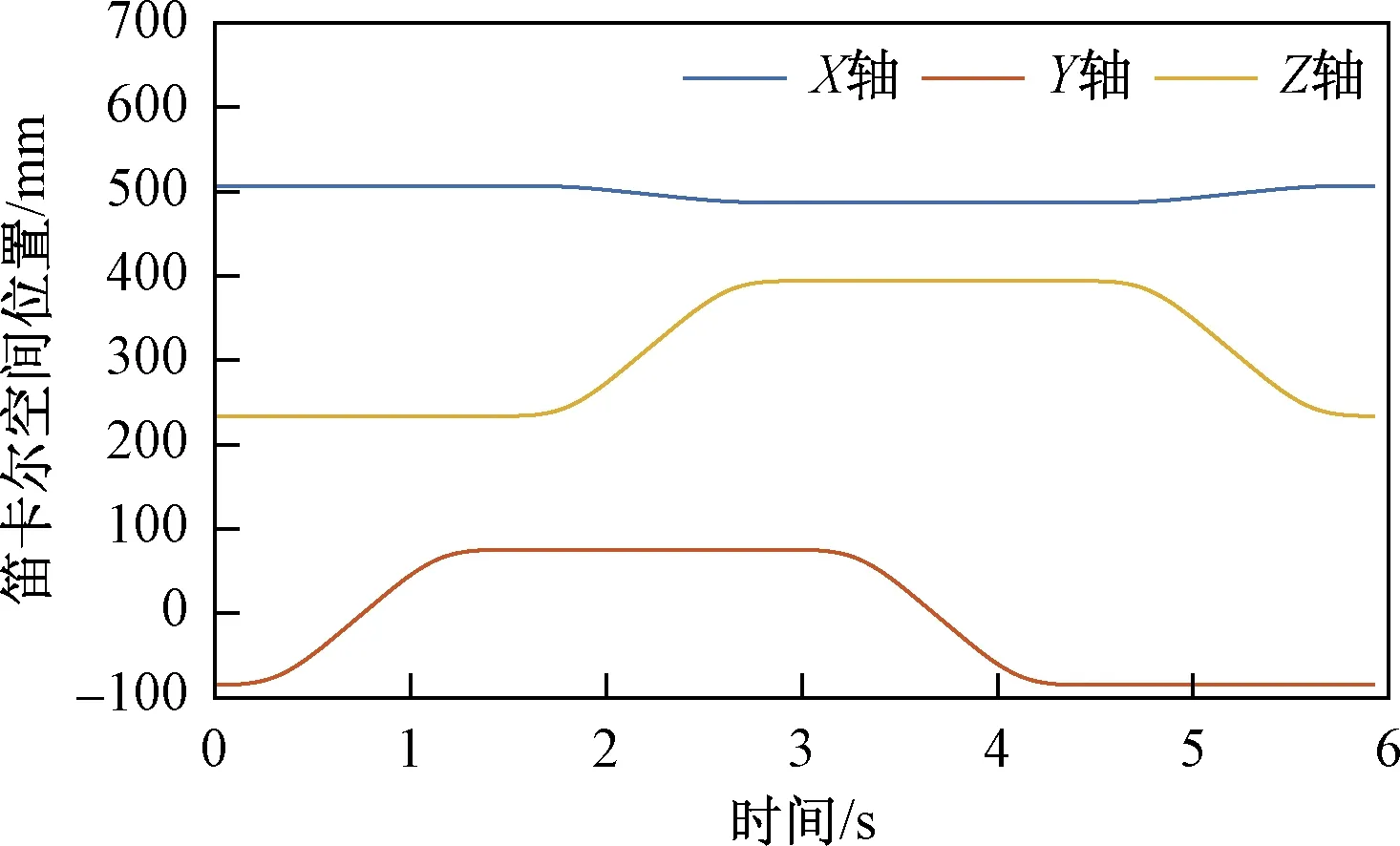
圖3 機(jī)械臂末端規(guī)劃位置Fig.3 Planned position of the end-effector of the manipulator

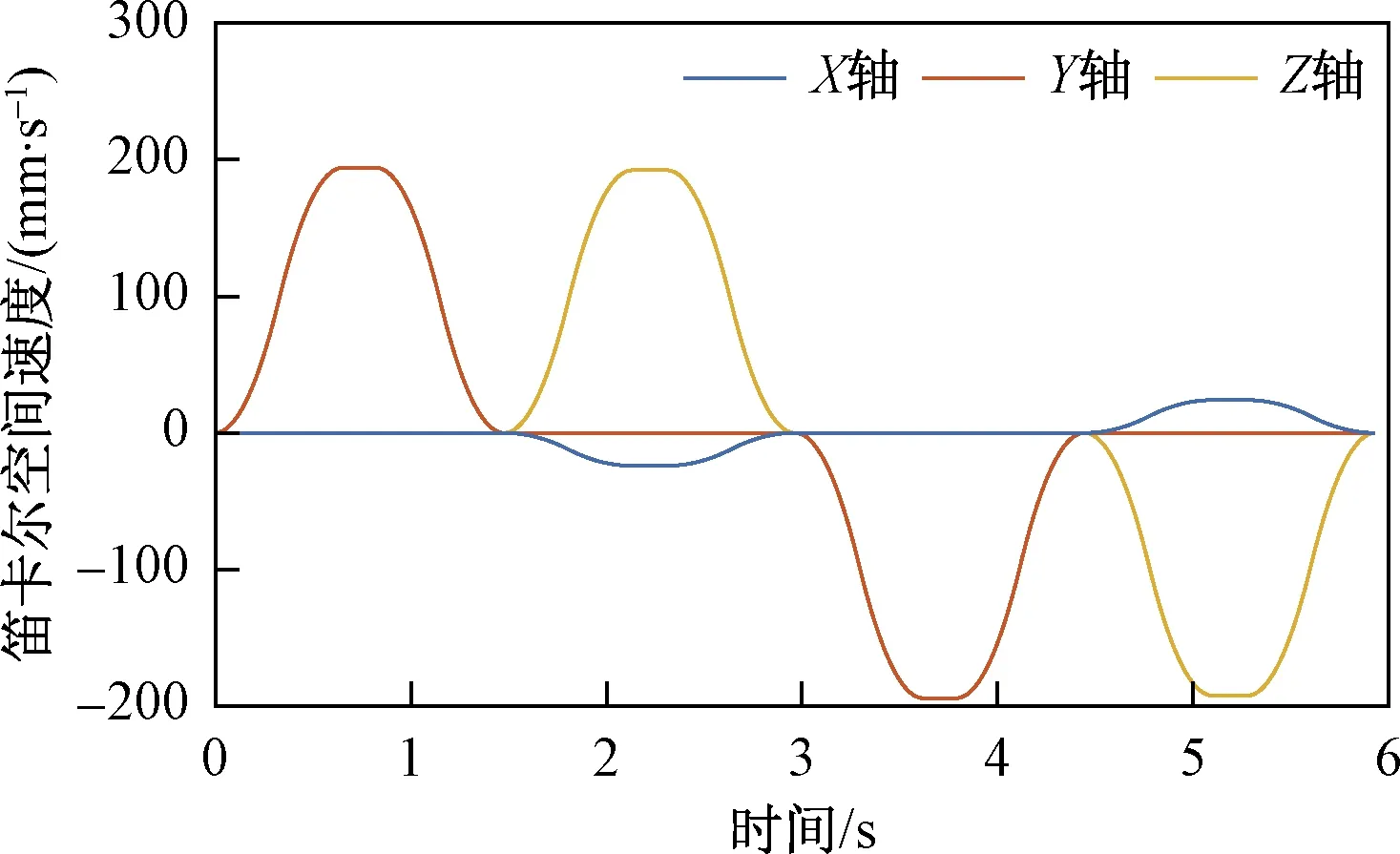
圖4 機(jī)械臂末端規(guī)劃速度Fig.4 Planned velocity of the end-effector of the manipulator

整個(gè)運(yùn)動(dòng)過程中，機(jī)械臂各關(guān)節(jié)的位置變化曲線如圖5所示。可以看出，曲線光滑連續(xù)，關(guān)節(jié)位置都在允許的范圍內(nèi)。在相同的起始位姿下，利用梯度投影法跟蹤同樣的空間封閉四邊形軌跡。如圖6所示，關(guān)節(jié)位置同樣沒有超出限位。兩種方法都利用運(yùn)動(dòng)學(xué)冗余對(duì)目標(biāo)函數(shù)實(shí)現(xiàn)了很好的優(yōu)化。

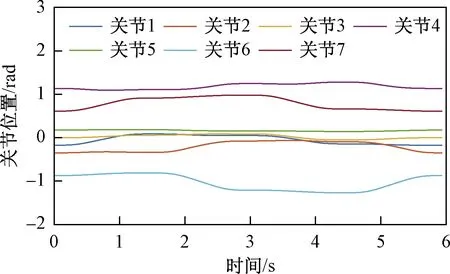
圖5 本文方法獲得的關(guān)節(jié)位置Fig.5 Joint position obtained by the proposed method

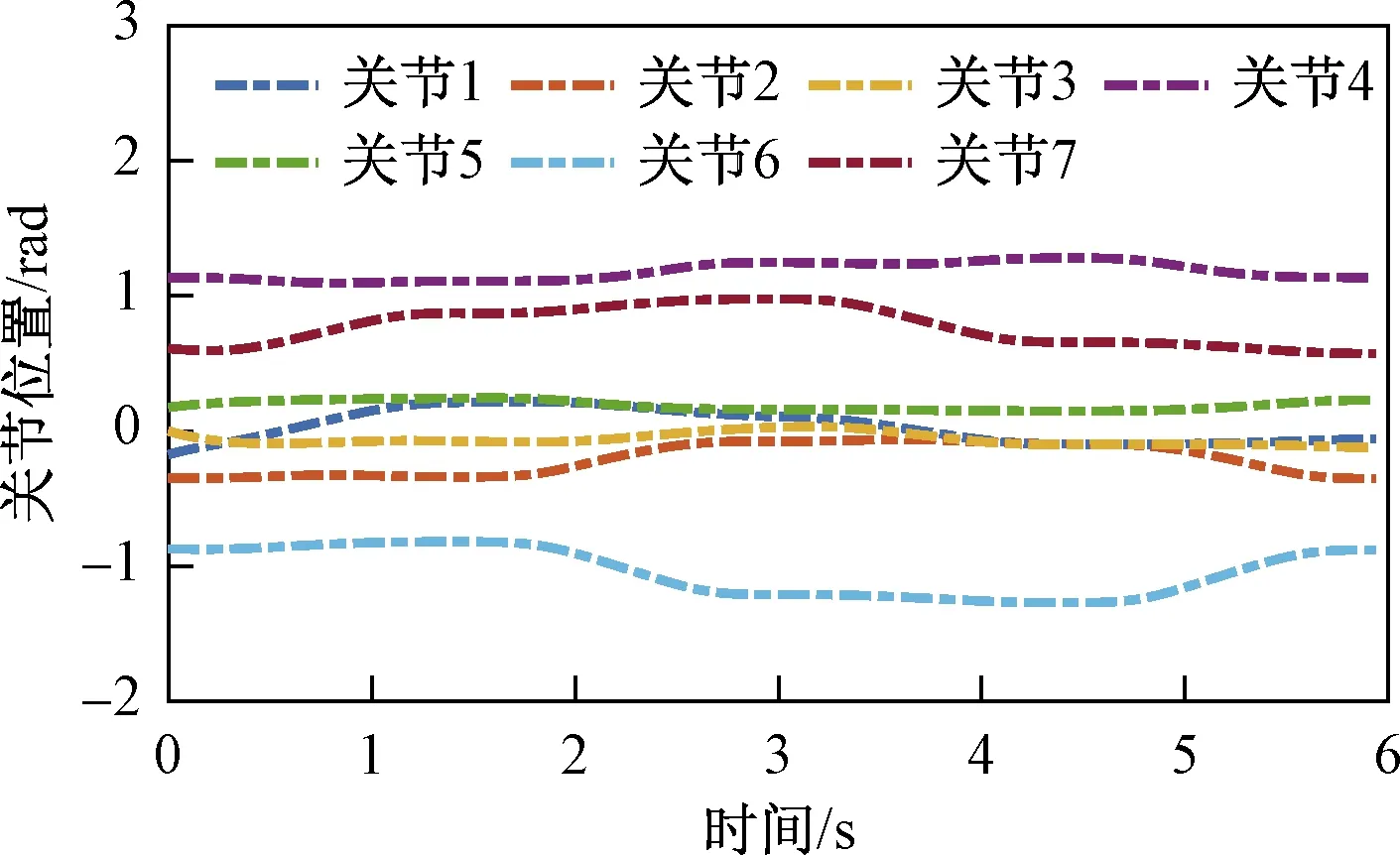
圖6 梯度投影法獲得的關(guān)節(jié)位置Fig.6 Joint position obtained by the gradient projection method

利用兩種方法跟蹤封閉軌跡后，各個(gè)關(guān)節(jié)始末位置的對(duì)比如表3所示。在機(jī)械臂末端回到起始位置時(shí)，本文方法使機(jī)械臂的位姿與初始位姿相同，這使得運(yùn)動(dòng)具有可重復(fù)性，而使用梯度投影法(gradient projection method，GPM)時(shí)，關(guān)節(jié)的最終位置相對(duì)于初始位置發(fā)生了偏移。

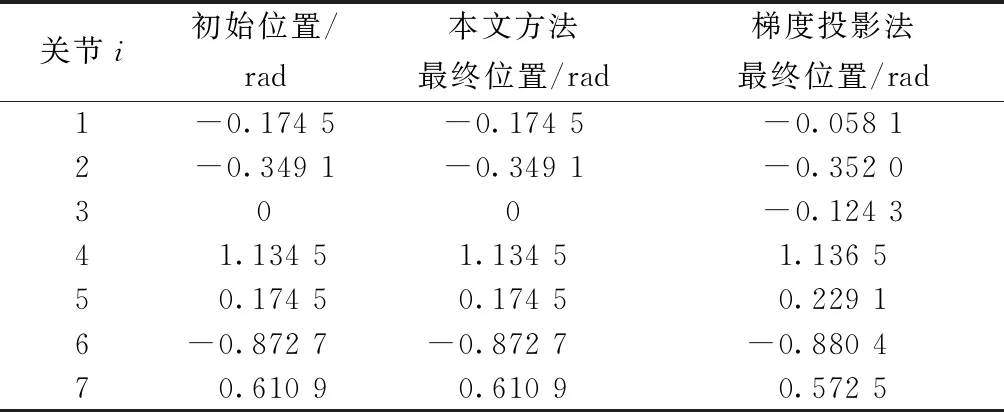
表3 機(jī)械臂關(guān)節(jié)始末位置對(duì)比

逆運(yùn)動(dòng)學(xué)問題求解的準(zhǔn)確性影響到機(jī)械臂跟蹤目標(biāo)軌跡時(shí)的精度，將兩種方法下的機(jī)械臂末端軌跡與期望軌跡進(jìn)行對(duì)比，得到如圖7所示的位置誤差。本文方法對(duì)軌跡實(shí)現(xiàn)了準(zhǔn)確的跟蹤，梯度投影法Z軸方向的誤差相對(duì)較大，X軸和Y軸方向的精度較高，但誤差仍略大于本文方法。本文方法相對(duì)于梯度投影法，在軌跡跟蹤過程逆運(yùn)動(dòng)學(xué)的精確求解上具有很好的表現(xiàn)。

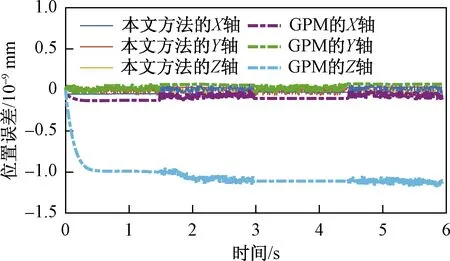
圖7 機(jī)械臂末端軌跡誤差Fig.7 Trajectory error of the end-effector of the manipulator

3.2 軌跡跟蹤實(shí)驗(yàn)

本文算法由C++實(shí)現(xiàn)，控制程序運(yùn)行在配置為Intel(R) Core(TM) i5-3437U 1.90 GHz CPU、4 GB內(nèi)存的PC上，由實(shí)時(shí)拓展套件KRTS(kithara realtime suite)提供PC的實(shí)時(shí)操作系統(tǒng)。實(shí)驗(yàn)系統(tǒng)的通信采用自主研發(fā)的EtherMAC(ethernet for manufacture automation control)[19]總線，通過網(wǎng)關(guān)與支持RS-485通信的機(jī)械臂連接，通信周期為8 ms。利用本文算法進(jìn)行10 000次逆解運(yùn)算，平均計(jì)算時(shí)間為176 μs，求解速度能夠滿足實(shí)時(shí)控制的要求。

如圖8所示，使機(jī)械臂執(zhí)行仿真時(shí)所采用的末端軌跡。循環(huán)運(yùn)動(dòng)3次，機(jī)械臂的關(guān)節(jié)位置、速度分別如圖9、圖10所示。可以看出，針對(duì)七自由度冗余機(jī)械臂，本文方法可保證逆運(yùn)動(dòng)學(xué)求解的準(zhǔn)確性，且關(guān)節(jié)位置、速度曲線平滑。同時(shí)，關(guān)節(jié)位置變化具有周期性，表明本文方法可保證機(jī)械臂運(yùn)動(dòng)的可重復(fù)性。

圖8 機(jī)械臂跟蹤規(guī)劃軌跡Fig.8 Manipulator tracking the planned trajectory

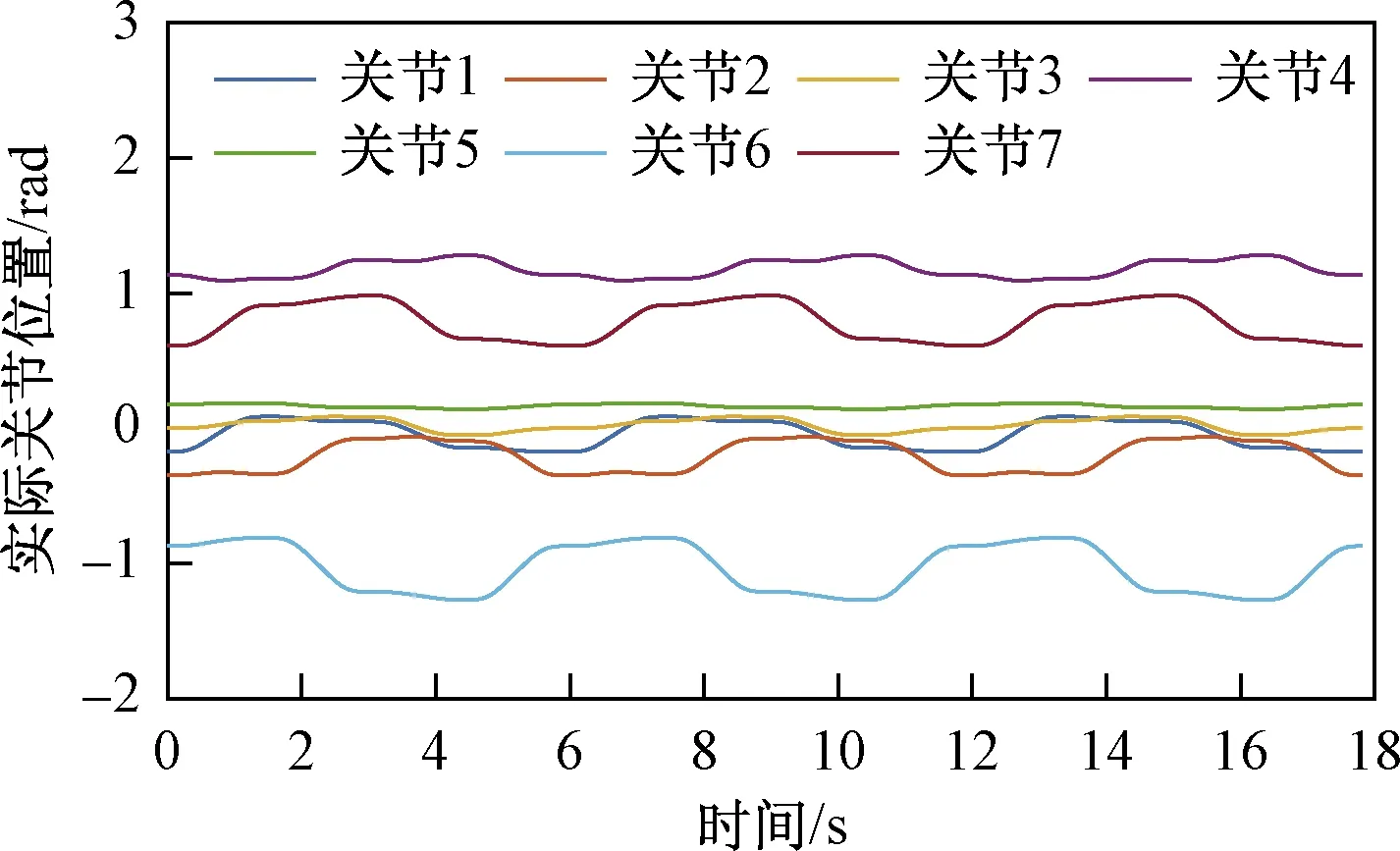
圖9 機(jī)械臂實(shí)際關(guān)節(jié)位置Fig.9 Actual joint position of the manipulator

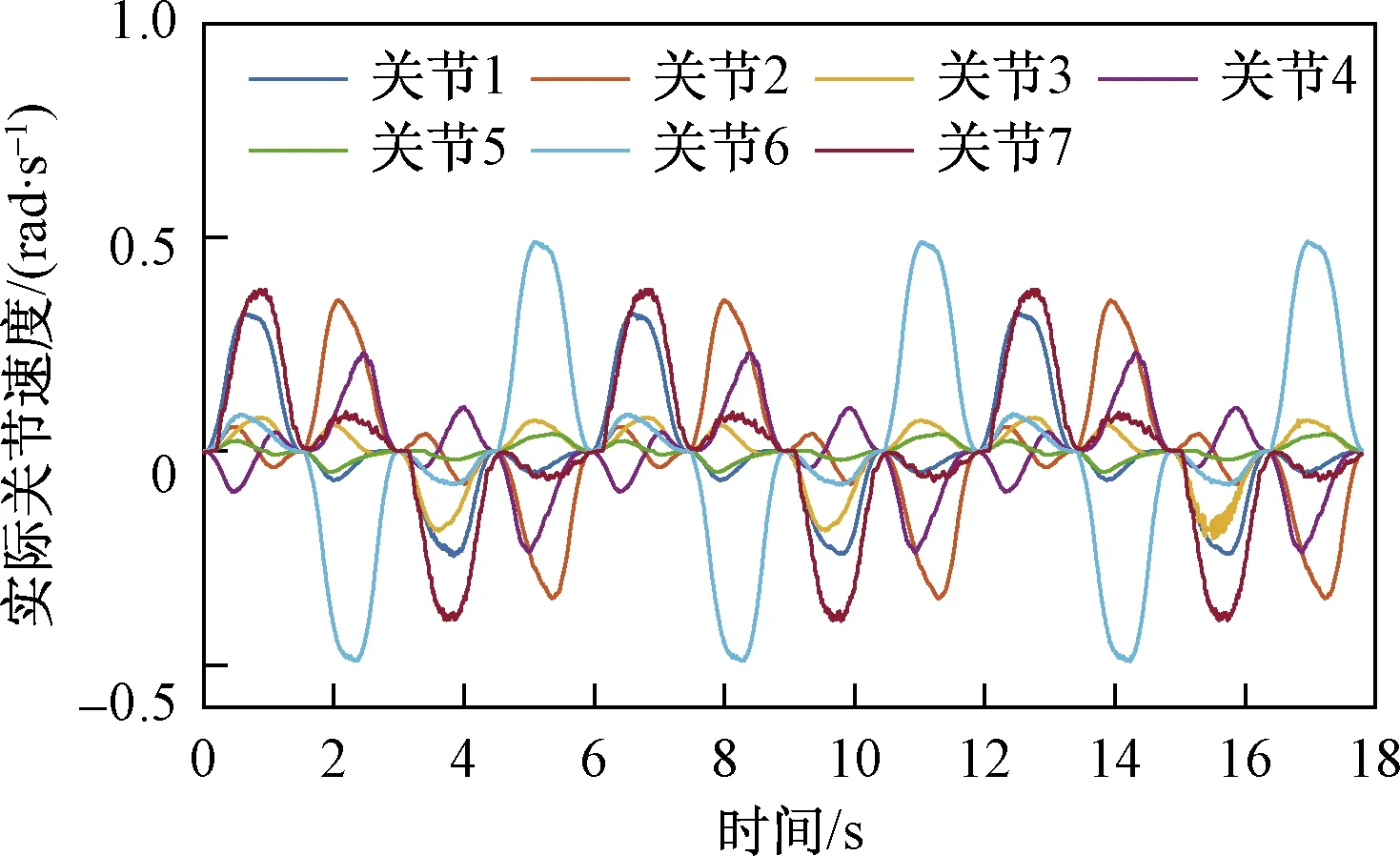
圖10 機(jī)械臂實(shí)際關(guān)節(jié)速度Fig.10 Actual joint velocity of the manipulator

4 結(jié)論

提出了一種利用增廣雅可比矩陣的冗余機(jī)械臂逆運(yùn)動(dòng)學(xué)求解算法。將優(yōu)化給定的目標(biāo)函數(shù)作為約束任務(wù)對(duì)機(jī)械臂的任務(wù)空間進(jìn)行增廣，在此基礎(chǔ)上構(gòu)造了增廣雅克比矩陣。針對(duì)機(jī)械臂關(guān)節(jié)數(shù)目較多時(shí)，增廣雅可比矩陣難以計(jì)算的問題，通過對(duì)其中的增廣部分采用分解后計(jì)算的方式實(shí)現(xiàn)了增廣雅可比矩陣的有效求解。仿真結(jié)果表明，相比于梯度投影法，本文方法具更高的求解精度，且能夠保證機(jī)械臂追蹤封閉軌跡時(shí)運(yùn)動(dòng)的可重復(fù)性。算法平均求解時(shí)間為176 μs，計(jì)算效率滿足實(shí)時(shí)控制的要求。通過七自由度冗余機(jī)械臂軌跡跟蹤實(shí)驗(yàn)，驗(yàn)證了本文方法的可行性和穩(wěn)定性。