富水區隧道圍巖多場參數反分析研究

寇海軍

（中鐵十九局集團第五工程有限公司 遼寧大連 116100）

1 引言

軟巖及高地應力水平下的中等強度巖體或節理發育的硬巖工程都存在蠕變效應，隨著地下工程向深部發展，常會遇到應力、滲流以及溫度耦合影響的蠕變問題。關于溫度、應力、滲流等耦合作用下巖體蠕變特性及其本構模型已開展了大量的研究工作。

黃書嶺等[1]、劉建等[2]通過試驗研究了耦合條件下巖石的蠕變與滲流、應力之間的關系。從數值模擬及本構模型的角度，郤保平等[3]、王永巖等[4]、MA L J等[5]研究了溫度場、應力場、化學場耦合條件下巖體的蠕變規律。無論是理論分析還是數值模擬均離不開巖體參數，其在工程設計與施工中起著至關重要的作用，參數反分析方法作為一種確定參數的有效手段，受到廣泛關注[6－7]。在蠕變參數反演方面，陳靜等[8]、徐國文等[9]提出相關反演方法，并在工程實際中進行應用。目前大多數研究針對單場參數反演，而對多場耦合下參數反演研究較少。賈善坡等[10]提出泥巖滲流－應力耦合蠕變損傷模型，采用優化反分析法得出蠕變損傷模型中的待定參數。劉開云等[11]將高斯過程回歸（Gaussian Process Regression，GPR）引入隧道工程進行模型參數反演，并采用單一各向同性核函數之和作為GPR的組合核函數以提高其泛化性能。孫錢程等[12]在改進多輸出支持向量機算法（MSVM）的基礎上，建立基于貝葉斯理論的概率反分析方法（B-MSVM方法）。

本文針對多場耦合下巖體蠕變參數較難獲得的問題開展反分析研究，基于免疫算法和BP神經網絡的應力－滲流耦合作用下隧道圍巖蠕變多參數反演方法進行。以蘭州至海口國家高速公路（G75）某石質特長隧道為工程實例，基于現場監測數據進行應力－滲流耦合條件下隧道圍巖蠕變多參數反演。

2 應力－滲流耦合蠕變模型

高地應力軟巖隧道圍巖具有明顯蠕變性，一般而言，將存在蠕變行為的總應變分解為彈性應變、塑性應變、蠕變應變，即：

式中：ε為總應變；εe為彈性應變；εp為塑性應變；εc為蠕變應變。

可依據需求在ABAQUS軟件中自行選擇蠕變定律，該軟件具有Singh-Mitchell、應變硬化及時間硬化三大蠕變定律可供選擇。

（1）時間硬化蠕變定律

（2）應變硬化蠕變定律

（3）Singh-Mitchell蠕變定律

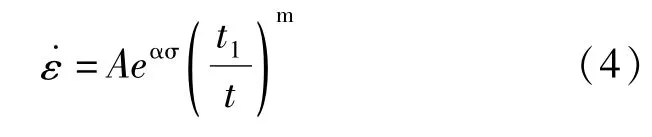
本文考慮蠕變非線性，采用時間硬化蠕變定律，巖石的總蠕變可以表示為

式中：εt為瞬態蠕變；εs為穩態蠕變。

對于瞬態蠕變和穩態蠕變可以采用冪次法則模式來描述：

式中：σ為等效應力；n為應力指數；A為蠕變系數；t為時間；m為時間指數。

本文取m＝0，則式（6）簡化為：

3 IA-BP多參數反演方法與實施

免疫算法能夠在尋求全局最優解過程中，對多峰值函數尋優出現的 “早熟”問題進行妥善處理。利用免疫算法優化BP神經網絡的權值與閥值，并建立IA-BP智能反分析方法，進行應力－滲流耦合隧道圍巖蠕變多參數反演。

采用ABAQUS軟件對基于正交試驗設計方法構造樣本，并對樣本參數進行計算作為IA-BP算法的樣本值。

在進行IA-BP算法參數反演前，對BP神經網絡隱含層和輸入層的參數進行設置，并對BP神經網絡結構參數進行初始化。

其次，對免疫算法的種群數、免疫基因數量等參數進行設置，其中BP神經網絡權重之和用基因個數D來表示。其隱含層、輸出層、輸入層神經元數量用S1、S2和R來代表，則粒子群維數公式：

計算抗原抗體的親和度，親和度函數：

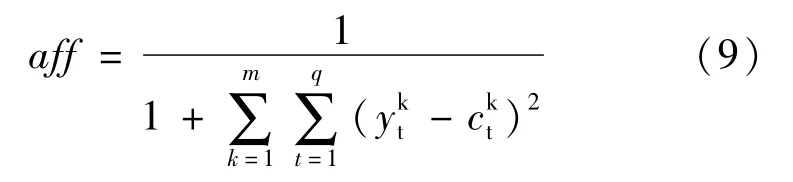
將神經網絡的輸入向量設定為圍巖位移量，輸出向量設定為隧道圍巖巖體參數，對隧道圍巖位移與圍巖參數之間的非線性關系建立關系函數。優化目標函數為：

式中：x為待反演參數；fi（x）為第i個量測方向的計算位移值；ui為第i個計算向量的實際位移；n為隧道圍巖位移監測點數量。

按照隧道實際尺寸進行數值建模，邊界影響條件考慮3倍洞徑，故幾何模型尺寸為橫向X軸50 m，縱向Y軸長度50 m，模型拱頂至上部邊界19.5 m，模型拱底至底部邊界22.5 m，如圖1所示。

圖1 有限元模型

隧道圍巖參數范圍如表1所示。本次數值計算共選擇6個試驗主控參數，對每個主控試驗參數選取5個水平因素，基于正交設計方法，選擇 L25（56）正交試驗表進行方案設計，正交試驗方案如表2所示。對正交試驗方案中的每組試驗參數進行對應的數值計算，借助ABAQUS軟件計算正交參數組下的圍巖位移值。

表1 巖體參數

表2 正交設計

通過MATLAB軟件，借助IA-BP智能算法，對表2正交設計試驗組中的圍巖參數與圍巖位移值建立非線性關系，通過反演得到IA-BP的學習樣本值。IA-BP智能算法學習值與計算試驗值數據對比如表3所示。

表3 試驗值與IA-BP算法對比

對試驗值與IA-BP算法值進行殘差值計算，計算結果如圖2所示。由圖2可知，除了滲透系數偏差較大外，其他各參數大多數點都在零附近。由表3與圖2可知，計算試驗值和反演值之間誤差較小，說明該算法對隧道應力－滲流耦合多參數反演具有較高的計算精度。

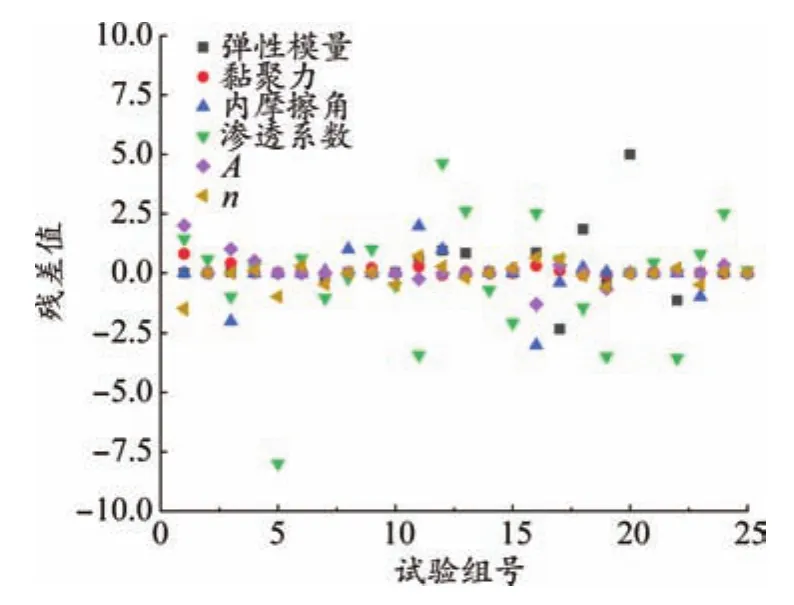
圖2 殘差值計算結果

將反演參數代入ABAQUS進行模擬可得到圍巖與支護結構的應力、位移以及塑性區分布。隧道完成開挖90 d后，及隨開挖步隧道圍巖位移變化云圖如圖3所示。當隧道完成第一、第二開挖步時，隧道拱頂圍巖發生較大位移變化；當完成第三步開挖及開挖完成后第90天的隧道圍巖位移變化較為平穩，此時隧道圍巖趨于穩定狀態。

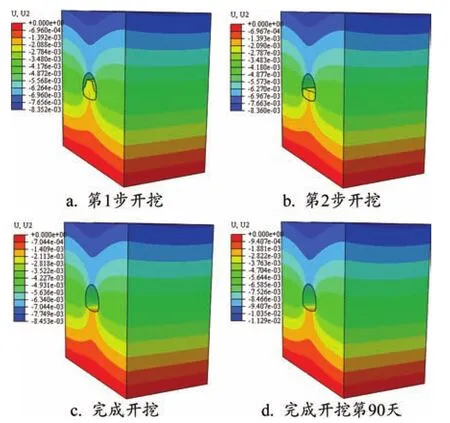
圖3 隧道圍巖豎向位移變化云圖

4 工程應用

4．1 工程概況

渭武高速公路土建第十七合同段起訖里程K345＋800～K350＋000，線路為分離式通行，雙線折合全長為8.4 km。某隧道為渭武高速隴南段特長隧道，為左、右雙洞分離式設計，左線工程段長度為3 009 m，渭武十七標承建出口端2 243 m；右線全長為3 209 m，渭武十七標承建出口端2 460 m。

4．2 基于現場監測數據的參數反演

該工程YK345＋907位置，隧道上斷面開挖后拱頂發生沉降、邊墻周邊收斂，在套拱前沉降達80 mm，周邊收斂達154 mm，收斂值為沉降值的1.925倍。施作套拱后拱頂沉降及周邊收斂速度明顯降低。下臺階開挖后圍巖被進一步擾動，拱頂沉降及周邊收斂發生突變，仰拱封閉后拱頂沉降及周邊收斂趨于穩定，最終拱頂沉降穩定于129 mm，周邊收斂穩定于263 mm。對數據進行分析發現，采用上下臺階法進行隧道開挖時，隧道圍巖水平收斂及拱頂沉降值之間差異較大，拱頂沉降值為94 mm，水平收斂值高達219 mm，在拱頂沉降最大值與水平收斂最大值中占比分別為72.3%及83.2%。其中，開挖過程引起的仰拱及下臺階沉降為36 mm，水平收斂值為44 mm，分別占最終沉降和收斂的27.7%和16.8%。

選取對數型及指數型函數對隧道位移數據進行回歸處理，擬合結果較為理想。沉降測點C1及收斂測線S1回歸結果如圖4、圖5所示。

圖4 隧道拱頂沉降擬合曲線

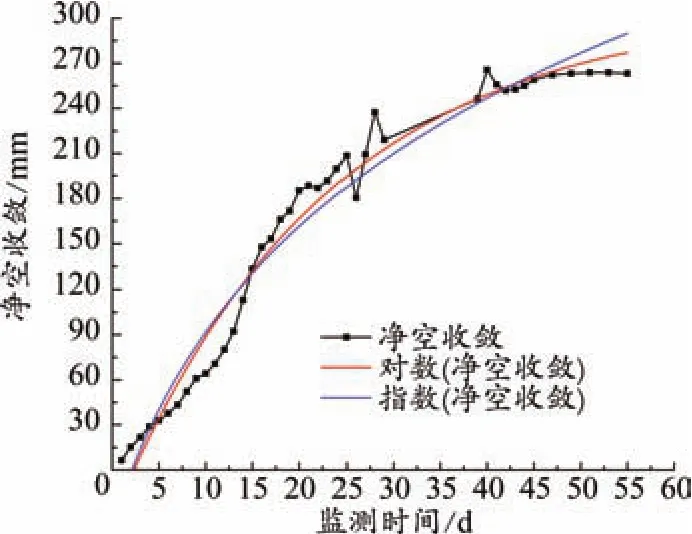
圖5 隧道收斂擬合曲線

基于監測數據，采用反分析方法進行參數反演，參數反演結果如表4所示。

表4 參數反分析結果

4．3 現場隧道突水與支護方案

隧道出口端右線掌子面施工至YK347＋792處，正在進行出渣作業時，線路左側上臺階拱腳以上1.5 m位置突然出現多處高壓股狀涌水，如圖6所示。出水量經初步測算約430 m3／h，2 h之后突水量基本穩定，經測算約260 m3／h，隧道涌水至二襯地段。突水水質渾濁，呈火山灰紅色，水流中伴有碎石、泥土等。突水發生之后，YK347＋807～YK347＋792段初期支護大面積涌水，發生多處環向、縱向開裂。

圖6 隧道掌子面突涌水

出水量穩定后及時對該段初期支護斷面進行沉降收斂監控量測，YK347＋798.852斷面順里程前進方向左側侵限30 cm，下沉11.7 cm；YK347＋804斷面順里程前進方向左側侵限7 cm，右側侵限3.6 cm，下沉5.4 cm。

通過參數反演對隧道穩定性進行分析，初期支護施作鋼拱架臨時仰拱，徑向設置三道工字鋼斜撐，如圖7所示。對各斷面進行 2次／d的加密監測，經數據分析于2017年1月15日沉降、收斂值基本趨于穩定。

圖7 隧道右線涌水后初期支護施作臨時仰拱及斜撐

5 結論

以蘭州至海口國家高速公路（G75）某隧道為工程實例，基于現場監測數據，采用建立的IA-BP算法進行應力－滲流耦合下隧道圍巖多參數反演，拓展了參數反演應用范圍。AI-BP算法對于多參數反演的精度較高，體現出其全局搜索最優解的特點，證明基于AI-BP算法的反分析方法是一種高效的多參數反演方法，可以用于應力－滲流耦合復雜環境下的隧道圍巖蠕變多參數反演。基于監測數據反演應力－滲流耦合下隧道圍巖蠕變多參數，各測點位移值與實測值基本吻合，即反分析得出的參數值為能夠反映隧道變形規律的“真實值”。根據反演參數進行隧道穩定性分析，實現了復雜環境下反分析與位移信息反饋動態設計相結合，為工程施工提供依據。