安全聯鎖設備SIL驗證中的參數估計偏差分析*

李敏睿，王海清，姚竣瀚，毛 奇

(中國石油大學(華東)安全科學與工程系，山東 青島 266580)

0 引言

國內化工企業尤其是涉及“兩重點一重大”的大型企業按照中華人民共和國應急管理部〔2014〕116號文《關于加強化工安全儀表系統管理的指導意見》的要求廣泛開展安全聯鎖系統評估與改造,以適應當前嚴峻的危化品安全生產形勢要求。安全完整性等級(SIL)，是衡量安全聯鎖系統安全水平的關鍵指標之一，即在一定時間和一定條件下，安全相關系統執行所規定的安全功能的概率[1]。根據功能安全標準IEC61508，SIL以聯鎖回路的平均需求時失效概率PFDavg作為驗證依據。

功能安全標準IEC61508(下文統一簡稱為IEC61508)計算PFDavg時均假設相關設備的失效率為恒定值[2](即壽命分布服從指數分布)，以化工安全設備為背景的PFDavg算法和SIL驗證中，安全管理人員均是采用恒定失效率計算。但實際中，設備由于老化[3]、疲勞磨損[4]等因素，絕大多數機械、電子設備[5]的失效率隨使用時間緩慢上升，在計算時導致PFDavg與實際值存在較大誤差。不僅如此，IEC61508針對不同應用范圍，推薦不同參數估計置信度[6]，影響SIL驗證的準確性，增加驗證的不確定性[7]，使得化工企業的生產裝置處于欠保護或者過保護的狀態，進而可能誤導風險評判結果。

鑒于此，本文定量比較研究安全聯鎖回路在恒定和非恒定失效率情況下的2種算法，并對存在的偏差進行定量評估分析，以更好落實《關于加強化工安全儀表系統管理的指導意見》在國內化工企業的應用。首先使用蒙特卡洛仿真，獲取符合工程實際的失效數據，進而使用極大似然估計求解出威布爾參數和指數參數，并運用威布爾分布PFDavg算法、指數分布PFDavg算法及IEC61508近似算法分別在70%和90%的2種典型置信度下得到3者PFDavg值隨預防性維修周期的變化趨勢，對SIL驗證結果的影響進行對比分析。

1 失效截尾數據的蒙特卡洛仿真

本文主要研究目的是對比安全聯鎖系統設備的失效數據組分別在IEC61508近似算法，指數分布算法與威布爾分布算法下的可靠性評估差異，在結合與參考了安全聯鎖設備失效數據庫、研究對象的大量歷史失效數據后，得出1組可信度較高的失效參數，后使用這組參數在蒙特卡洛仿真中模擬生成一系列失效數據。這種方法能夠滿足本文同時針對指數分布參數估計和威布爾分布參數估計的需求。根據蒙特卡洛仿真的原理[8]，基于MATLAB設計蒙特卡洛仿真算法流程，如圖1所示。

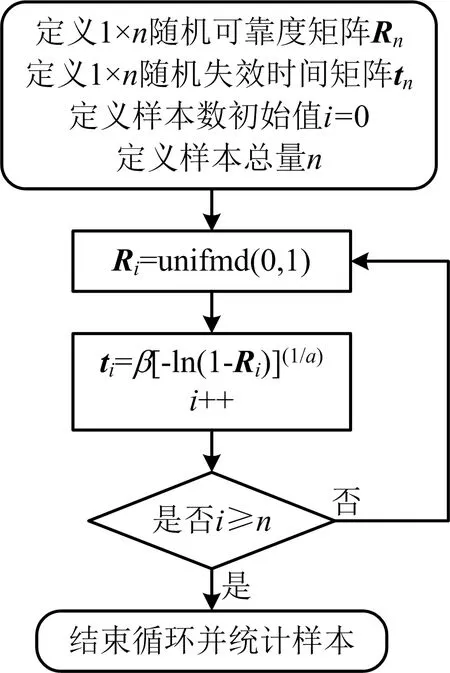
圖1 基于MATLAB蒙特卡洛仿真算法流程

蒙特卡洛仿真使用的仿真方法為概率積分變換方法，這種方法是將任意隨機變量轉換為均勻分布的隨機變量，代入概率密度分布函數的逆函數，循環多次計算得到一系列失效時間樣本值。

2 參數的極大似然估計

2.1 威布爾分布參數估計

假設失效數據服從威布爾分布，運用極大似然法和試錯法求出威布爾分布的形狀參數α和尺度參數β的估計值。使用極大似然法[9]求解威布爾參數估計值，如式(1)所示：

(1)

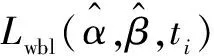
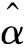
(2)

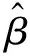
(3)

將式(3)帶入式(2)中，如式(4)～(5)所示：

(4)

(5)

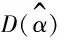
2.2 指數分布的參數估計

假設失效數據服從指數分布，可由指數分布I型截尾數據下的極大似然法求出失效率λ，指數分布的極大似然估計函數，如式(6)所示：

(6)

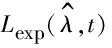
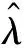
(7)

2.3 參數的置信區間估計

根據IEC61508，參數估計的置信度η不低于70%，同時在用于判斷結構約束時要求置信度η不低于90%[10],在極大似然法估計的基礎上，對參數進行不同置信區間估計以得出區間估計值。分別以70%和90%置信度為條件，研究和對比可靠性參數的區間估計值及其影響。

依據指數分布參數的區間估計算法[9]，可計算出指數參數估計區間[λL,λU]，如式(8)～(9)所示：

(8)

(9)

式中：η為區間估計的置信度；λL為指數參數區間估計下限值；λU為指數參數區間估計上限值；T為所有樣本的總失效時長，h；χ2為卡方分布。

依據威布爾分布參數的區間估計算法[9,11]，可計算出不同置信度下形狀參數和尺度參數的估計區間，對于α的估計區間[αL,αU]，如式(10)～(11)所示：

(10)

(11)

式中：αL為形狀參數的區間估計下限值；αU為形狀參數的區間估計上限值。

對于β估計區間[βL,βU]，如式(12)～(13)所示：

(12)

(13)

式中：βL為尺度參數區間估計下限值；βU為尺度參數區間估計上限值；d1和d2分別為中間系數。

對于d1和d2計算，如式(14)～(18)所示：

(14)

(15)

(16)

(17)

(18)

式中：A3,A4,A5和A6分別為區間估計的中間系數；x為標準正態分布的1-η分位點。

3 化工安全聯鎖設備的PFDavg算法和SIL驗證

工程中為保證安全聯鎖系統在發生緊急情況時正常運行，定期執行設備的預防性維修計劃(PM)，在這個周期里進行1次檢修和維護。記T0為設備的預防性維修周期，給出求解緊急放空執行單元PFDavg的3種算法[12]。

(19)

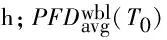
(20)

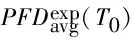
(21)

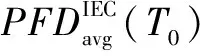
4 案例分析

以某蠟油加氫裝置的典型安全聯鎖系統回路[13]的緊急放空閥(EDV)為例(注：視為1oo1結構，現場實際的EDV為1用1備)。該回路中，催化加氫反應器的頂部氣相產物，經過熱高壓分離器分離的熱高分氣體進入熱高分氣換熱至184 ℃，再經過熱高分器空冷器A01001冷卻至50 ℃后進入冷高壓分離器。自冷高壓分離器頂部出來的循環氫經脫硫塔入口分液罐分液后，進入D03001循環氫脫硫塔底部，緊急放空閥的聯鎖回路，如圖2所示。

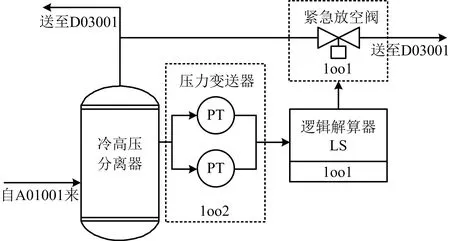
圖2 緊急放空閥的聯鎖回路

該回路中，由壓力變送器PT實時監測冷高壓分離器內壓力，并將數據傳至邏輯解算器LS單元，當冷高壓分離器內壓強超過2.1 MPa時，由邏輯解算器LS提供觸發信號給緊急放空閥，打開閥門以0.7 MPa/min的泄壓速率將超壓氣體排出。

結合SIS失效數據庫中緊急放空閥的失效統計數據[14]，以及參考實際工程中服從威布爾分布的緊急放空閥失效參數，設置形狀參數為1.49，尺度參數為6 025 003，通過蒙特卡洛仿真模擬生成200組隨機失效數據。

根據加氫裝置實際運行的情況，在得到模擬樣本后，進行截尾時長為175 200 h的I型截尾處理，得到150組完整失效數據和50組截尾失效數據。需要強調的是，采用蒙特卡洛模擬的截尾失效數據作為測試數據，并不影響比較統計分析的有效性，且可以比實際的工程采集數據提供更客觀的誤差分析結果[15]。

使用試錯法，先是試錯α估計值區間的選取，考慮到設備運行周期內失效率是1個緩慢上升的過程，并查閱相關閥的失效參數庫，得知α值在1.0至1.7范圍內，因此試錯值假設在該區間，依次帶入式(4)，求得α估計值偏差量，并求得似然估計求解的α和β估計值，如表1所示。

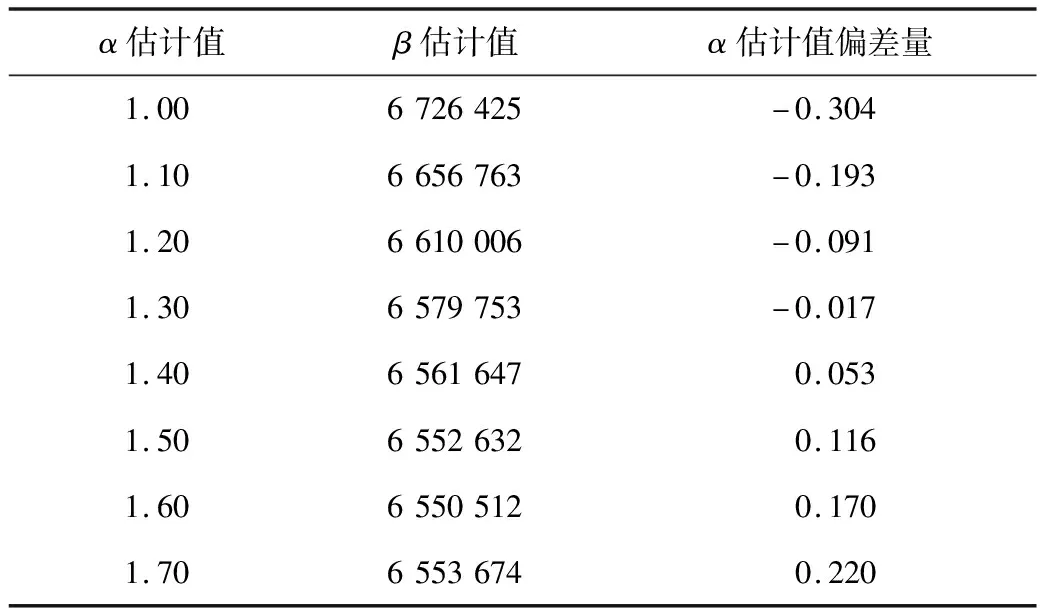
表1 似然估計求解α和β估計值

由表1計算得到的數據，繪制α估計值偏差量與β估計值雙坐標曲線，如圖3所示。

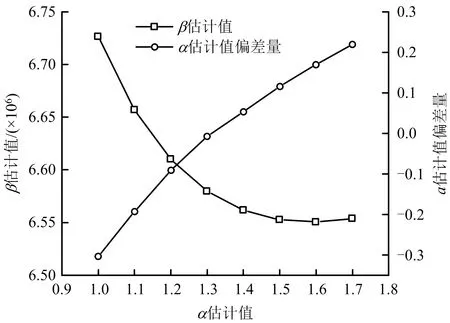
圖3 α估計值偏差量與β估計值曲線

根據式(14)～(18)，威布爾區間估計可算出70%置信度時d1=0.124，d2=-0.116，90%置信度時d1=0.198，d2=-0.198，代入式(12)～(13)中，算出β估計區間的上限值和下限值。

表2 威布爾分布和指數分布的參數估計區間

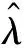
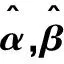
表3 70%和90%置信度時和估計值

分別在70%和90%這2種不同的參數估計置信度下，研究不同T0時，威布爾分布，指數分布和IEC61508的PFDavg計算結果的變化曲線，并分析這3種算法結果的差異。結合工程實際，為便于比較將安全聯鎖設備的T0分別取1，2，3，4，5 a。得到70%和90%置信度時3 種算法的PFDavg變化趨勢。70%置信度下3種算法的PFDavg與T0關系，如圖4所示；90%置信度下3種算法的PFDavg與T0關系，如圖5所示。

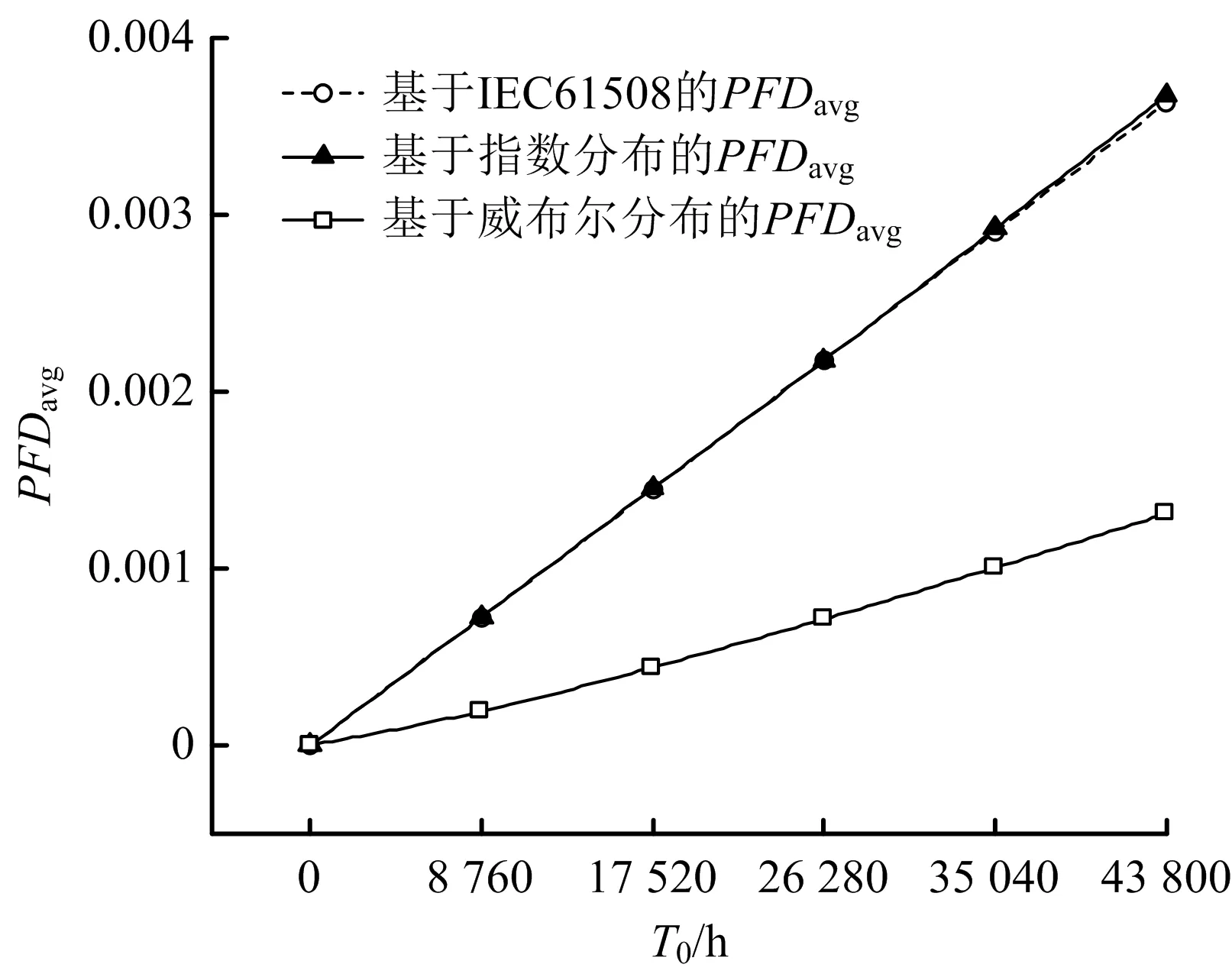
圖4 70%置信度下3種算法的PFDavg與T0的關系

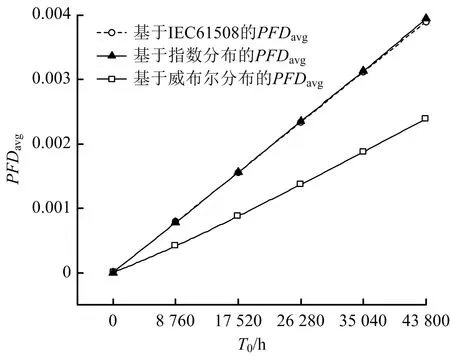
圖5 90%置信度下3種算法的PFDavg與T0的關系

由圖4～5可知，70%和90%置信度下指數分布和IEC61508的PFDavg曲線差值均較小，證明IEC61508簡化算法替代指數分布算法的合理性。

鑒于指數分布和IEC61508的2種算法的計算結果相差不大，因此將僅在70%和90%置信度時分析指數分布算法與威布爾分布算法的PFDavg計算值之間的相對誤差和絕對誤差，并進行對比。指數分布與威布爾分布PFDavg的相對誤差分析，如圖6所示；指數分布與威布爾分布PFDavg的絕對誤差分析，如圖7所示。

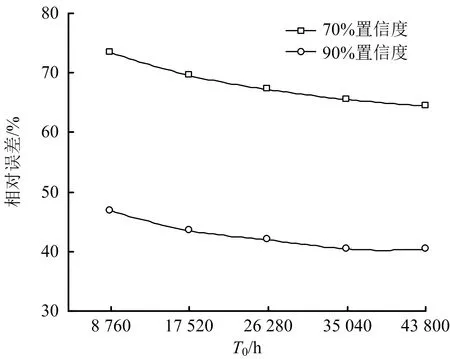
圖6 指數分布與威布爾分布PFDavg的相對誤差分析

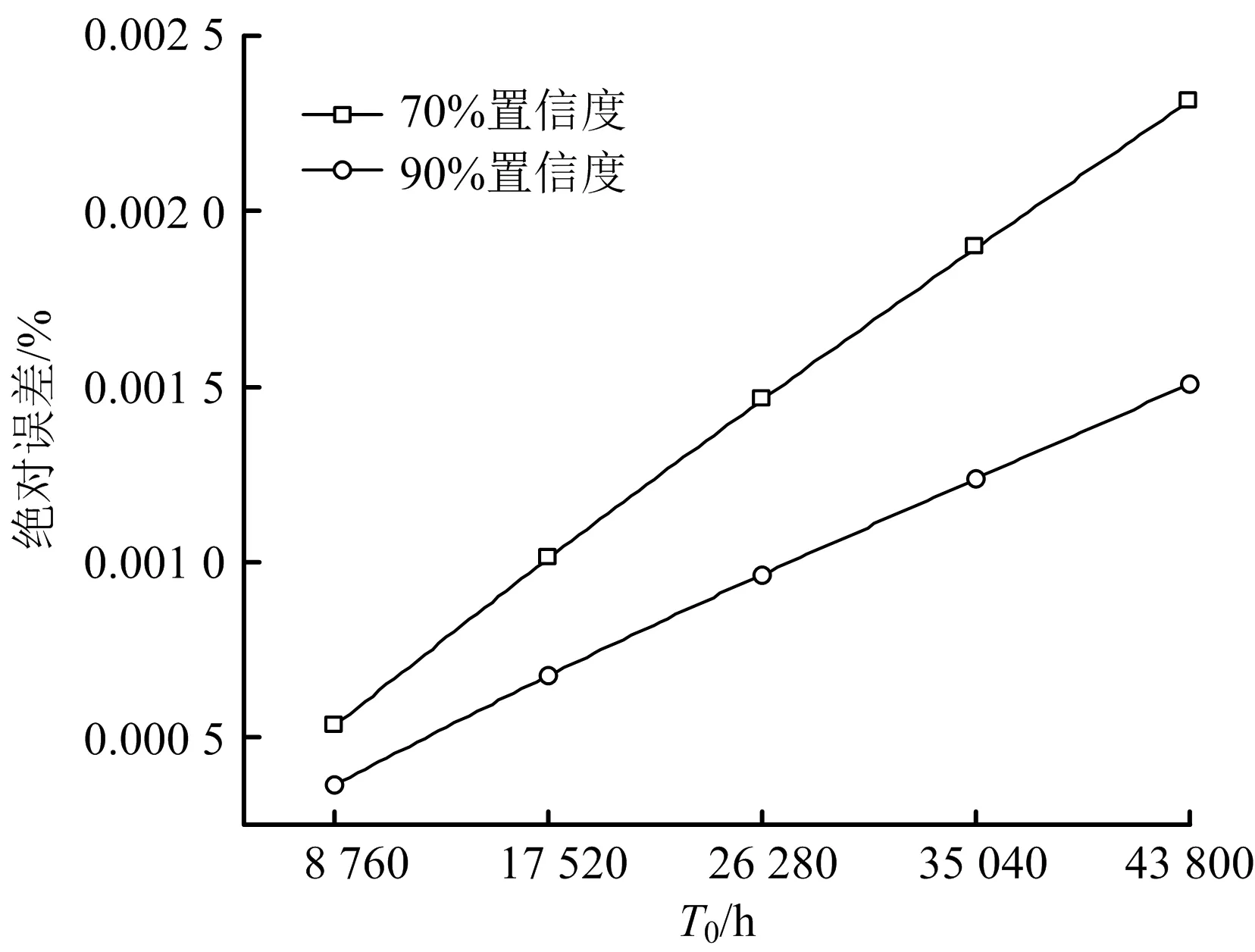
圖7 指數分布與威布爾分布PFDavg的絕對誤差分析

IEC61508算法的PFDavg值隨著T0的增大，絕對誤差(即IEC61508和指數分布PFDavg相比于威布爾分布PFDavg的數值偏差)增大，而相對誤差值減小。絕對誤差作為SIL驗證中數值誤差的直接表現，表明在指定預防性維修周期內存在較大誤差，證明工程上壽命服從威布爾分布的設備，簡化為采用指數分布算法計算其PFDavg的不合理性，并將導致顯著的風險研判偏差。

指數分布和IEC61508算法的SIL驗證結果基本一致，2者的驗證結果不再區分考慮。根據IEC61508中對SIL驗證的等級劃分規則，得出70%置信度時2種PFDavg算法的SIL驗證結果，如表4所示；90%置信度時2種PFDavg算法的SIL驗證結果，如表5所示。

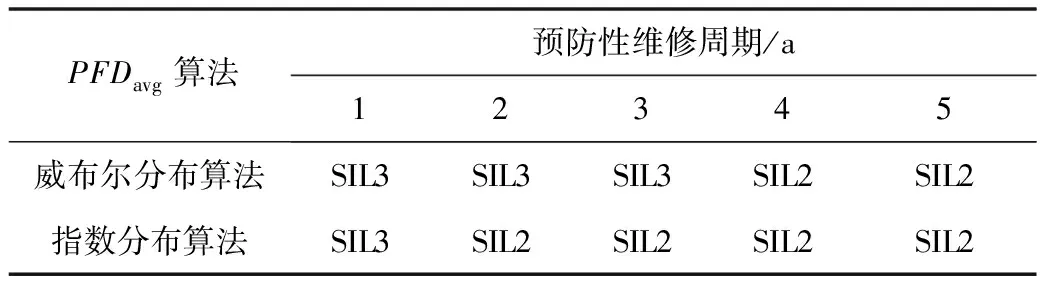
表4 70%置信度時2種PFDavg算法的SIL驗證結果

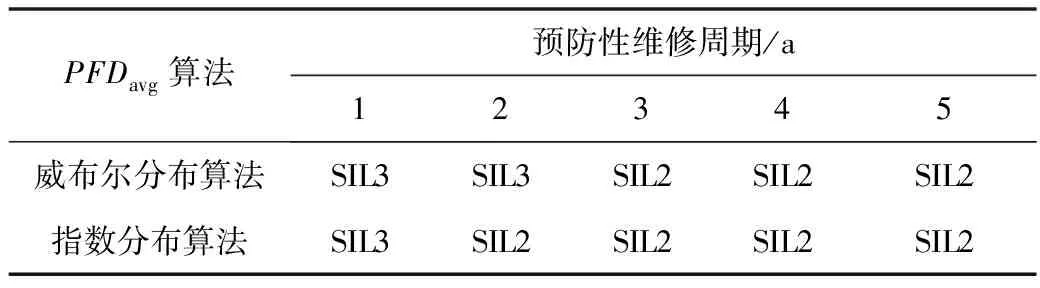
表5 90%置信度時2種PFDavg算法的SIL驗證結果

用模擬的方法得出，對于通過SIL驗證等級為SIL2的設備，如果實際壽命服從威布爾分布，則實際SIL驗證是有可能達到SIL3的。在表4～5中，預防性維修周期為1～3 a時，由威布爾分布算法得到的SIL驗證結果普遍比指數分布和IEC61508算法的SIL驗證結果高1個等級，可見服從威布爾分布的設備在使用IEC61508算法進行計算時將存在相當大的偏差，導致化工企業SIS升級改造項目投資過大。70%與90%置信度下的威布爾分布算法的SIL驗證結果存在一定差異，考慮到高置信度下計算得到的PFDavg值高于低置信度計算PFDavg值，在PFDavg數值計算使用70%置信度，結果較為折中，而使用90%置信度結果較為保守，驗證了IEC61508中，PFDavg算法推薦置信度為70%，數據采集和處理推薦置信度為90%的這一建議基本合理。

5 結論

1)對于聯鎖回路的執行單元等容易發生機械疲勞磨損的設備，其失效率在使用過程中緩慢上升，因此宜使用威布爾分布對設備失效時間數據進行分析和PFDavg計算；此外本文案例雖考慮的是1oo1結構，整個計算流程亦適用于其他表決結構。

2)如果對于壽命服從威布爾分布的設備，使用IEC61508算法計算的PFDavg可能會造成SIL驗證的誤差，低估了設備可以達到的SIL級別，造成化工廠的SIS改造投資增大。

3)區間估計的置信度越高，IEC61508算法計算的PFDavg與實際PFDavg偏差越小。隨著預防性維修周期的延長，在相同置信度下IEC61508的PFDavg與實際PFDavg間的相對誤差減小，絕對誤差增大。因此化工企業的允許短周期維護的聯鎖回路策略，采用IEC61508以及高置信度參數估計的驗證結果基本可信。