考慮滾動阻抗的線性接觸模型離散元宏細觀參數敏感性研究*

馬少坤,黃 驍,韋榕寬,劉 瑩,段智博

(1.廣西大學 土木建筑工程學院，廣西 南寧 530004;2.廣西大學 工程防災與結構安全重點實驗室，廣西 南寧 530004)

0 引言

巖土體作為1種天然的工程材料，其復雜的工程特性在生產實踐中常常引發不可預知的安全事故，例如邊坡失穩[1]、隧道塌方[2]等。而Cundall于20世紀70年代提出的離散元法為研究巖土的相關特性提供1種有效手段[3]，對工程安全具有重要意義。離散元法的核心接觸模型區別于傳統土力學理論中的宏觀本構模型，主要由顆粒與顆粒間的細觀接觸特性及參數所表征[3-4]。然而在實際工程和試驗中所測得巖土體的變形或強度特性均以宏觀參數來體現，這使得在利用離散元法對土體進行仿真模擬時，選取與其匹配的接觸模型及細觀參數較困難。

大量學者針對接觸模型細觀參數與土體宏觀力學參數的關系進行定量研究。曾遠等[5]利用PFC2D離散元分析軟件，進行多組無黏性土雙軸模擬試驗，詳細分析細觀參數對土體宏觀特性的影響;陳亞東等[6]建立多組不同細觀參數的模擬真三軸數值試驗，分析無黏性土細觀參數與宏觀參數的關系，并提出針對無黏性土的細觀參數確定方法；徐小敏等[7]開展一系列基于線性接觸模型的模擬試驗，分析顆粒細觀參數與試樣宏觀參數的關系，并建立經驗公式。上述基于無黏性土的細觀參數研究均以“ball”為基礎單元，鮮有考慮真實土顆粒的形狀效應，即忽略土顆粒之間的抗轉動作用；而Iwashita等[8]通過試驗發現顆粒間的抗轉動作用對顆粒的力學性質有顯著的影響。因此，部分學者也對抗轉動模型進行研究[9]。

此外，為探討宏細觀參數間的非線性關系，利用計算機算法對模擬數據進行分析。周喻等[10]采用BP神經網絡方法對400 組細觀力學參數隨機組合的三軸模擬試驗數據建立宏觀力學參數與細觀力學參數的非線性模型，結果表明此模型可快速、準確地反演巖土體的非線性關系；李澄清等[11]利用25組雙軸壓縮離散元數值試驗模擬結果建立BP人工神經網絡反演系統，結果表明模型反演性能較好；崔洋洋[12]開展多組基于線性接觸模型的雙軸壓縮試驗，利用BP人工神經網絡分析方法尋找宏-細觀參數之間的映射關系。

綜上所述，本文基于抗轉動線性接觸模型，采用控制變量法開展一系列三軸試驗數值分析，通過對比不同細觀參數下的模擬試驗結果，研究模型的不同細觀參數對宏觀參數的影響；針對對比試驗無法體現出參數交互作用這一難題，引入隨機森林機器學習法，詳細探究宏細觀參數的權重關系。

1 模型驗證及結果

1.1 計算參數選取

為研究模型細觀參數的敏感性，基于已有試驗數據開展相應的數值試驗以獲得1組合理的土體基本細觀參數。基于文獻[13]，選取豐浦砂為模擬對象，選取相關計算參數，見表1。

表1 計算參數

此外，采用擴大顆粒粒徑的方法保證計算效率。通過多次試算，最終選取由3 018個顆粒組成的試樣，該數量足以反應材料特性[7],級配曲線對比如圖1所示。最終標定結果見表2。

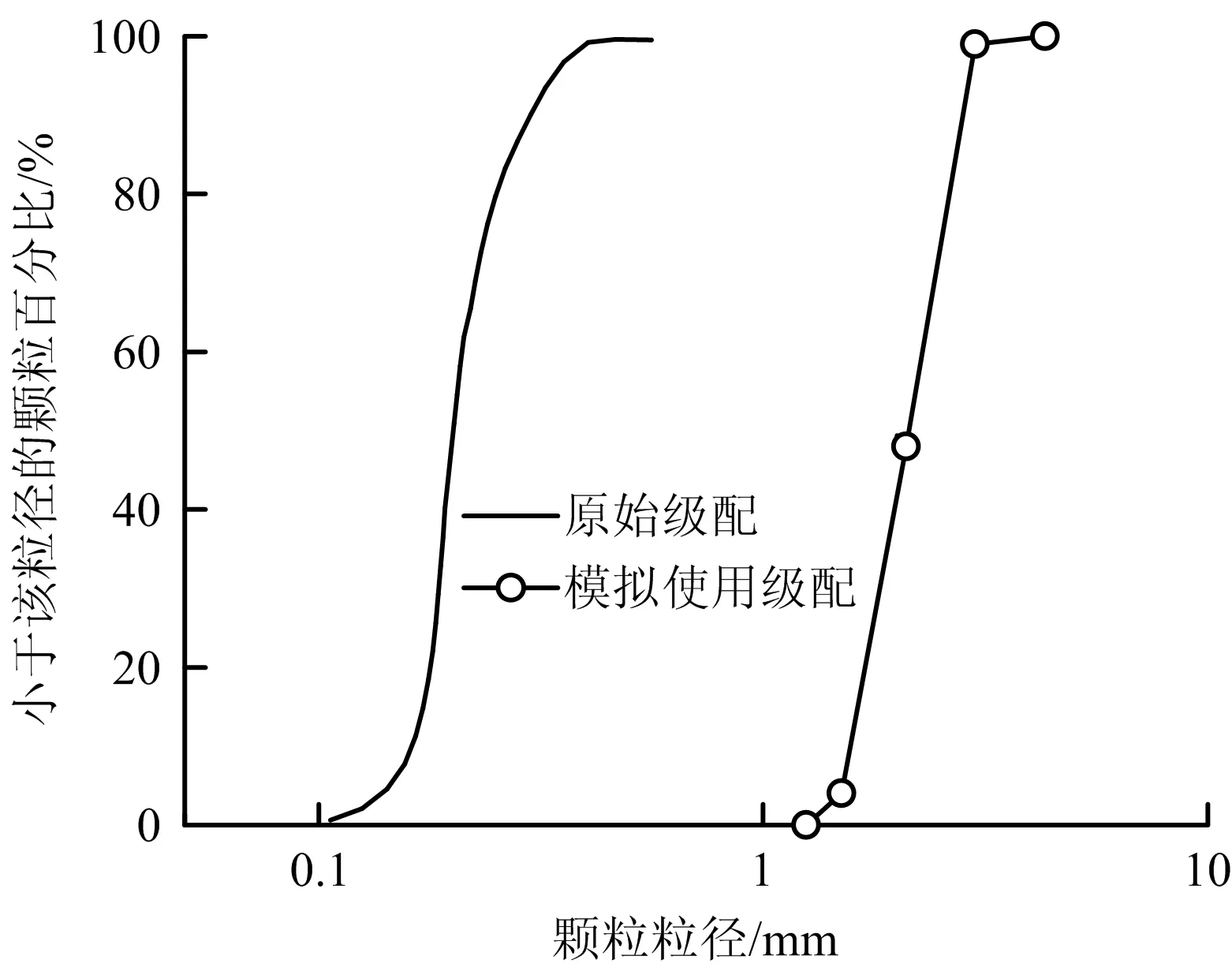
圖1 原始級配與模擬級配曲線

表2 豐浦砂標定參數

1.2 模擬結果

豐浦砂三軸固結排水壓縮室內試驗與數值試驗的結果對比如圖2～3所示。由圖2～3可知，在試驗初期，式樣的總體積減小，而偏應力-軸應變曲線近似為直線。隨著試驗不斷進行，試樣出現剪脹的趨勢，而偏應力的增長不斷放緩，直至到達峰值后，偏應力逐漸下降。總體而言，模擬結果與室內試驗的結果契合度均較好，整體誤差較小，證明利用該組細觀參數可較好地表征豐浦砂。

圖2 豐浦砂室內試驗與數值試驗偏應力-軸應變曲線對比

圖3 豐浦砂室內試驗與數值試驗的體應變-軸應變曲線對比

2 參數敏感性分析

在土體參數標定中，將土體宏觀參數(包括初始彈性模量、泊松比、峰值強度等)與模型細觀參數相對應。根據徐小敏等[7]的研究，在離散元三軸模擬試驗中，當試樣的軸向應變處于峰值應力所對應軸向應變的1%范圍內時，可視為試樣處于彈性形變階段。可根據此范圍內的偏應力-軸應變曲線與體應變-軸應變曲線計算出試樣所對應的初始彈性模量與泊松比，如式(1)～(2)所示：

(1)

(2)

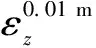
為研究和表征出各個細觀參數對宏觀參數的影響，基于本文所得豐浦砂對應的模型參數，為各個細觀參數設計進行對比試驗，模擬試驗方案見表3。

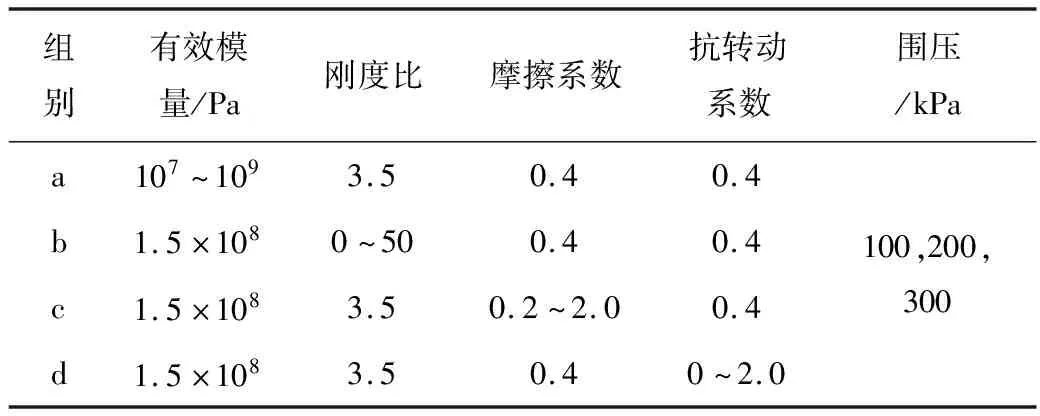
表3 模擬試驗方案

2.1 有效模量的影響

有效模量會顯著影響試樣的初始彈性模量。不同圍壓下有效模量與試樣初始彈性模量的變化規律如圖4所示。由圖4可知，二者呈正相關關系。即試樣的初始彈性模量隨著有效模量的增大而增大。這是因為當顆粒間有效模量增大時，顆粒間法向剛度與切向剛度隨之增大，而三軸試驗中上下加載板的加載速率保持恒定不變，因此在試樣加載過程中，顆粒間的變形等速率增加，而顆粒間法向剛度與切向剛度增大導致其接觸力變大，故在試樣處于較小的且相同的軸應變時，有效模量越大的試樣的軸應力越大，從而在宏觀上體現為顆粒間有效模量的增加會顯著增大試樣的初始彈性模量。

圖4 不同圍壓下初始彈性模量隨有效模量變化規律曲線

此外，有效模量的變化還會對試樣的泊松比產生影響。不同圍壓下泊松比隨有效模量變化規律曲線如圖5所示。由圖5可知，泊松比會隨著有效模量的增大而增大。這是因為當顆粒間有效模量增大時，顆粒間法向剛度和切向剛度隨之增大，而試樣處于軸向加載速率不變的條件下，顆粒間的徑向合力會增大，此時伺服側壁需要更大的徑向位移以保證圍壓的恒定，在宏觀參數上表現為泊松比隨之增大。

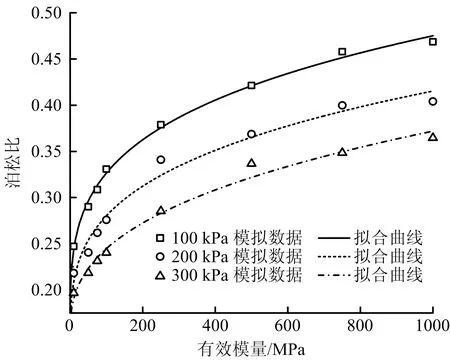
圖5 不同圍壓下泊松比隨有效模量變化規律曲線

2.2 剛度比的影響

剛度比的變化會顯著影響土體初始抗變形能力。不同圍壓下泊松比隨剛度比變化關系曲線如圖6所示。由圖6可知，試樣的泊松比隨剛度比的增大而增大。這是因為當顆粒的有效模量不變時，剛度比的增大使得顆粒間的切向剛度不斷減小，剪切帶內部顆粒可提供的接觸力徑向合力不足以與圍壓保持平衡。因此試樣內部需調動更大范圍的顆粒來平衡外部圍壓，造成更大范圍內顆粒的相對滑移，從而使試樣產生更大的徑向變形。因此剛度比的增大會導致試樣整體的切向抗變形能力下降，在宏觀參數上反映為泊松比隨剛度比的增大而增大。

圖6 不同圍壓下泊松比隨剛度比變化關系曲線

此外，剛度比還對試樣的初始彈性模量產生影響。不同圍壓下初始彈性模量隨剛度比變化關系曲線如圖7所示。由圖7可知，初始彈性模量會隨著剛度比的增大而不斷減小，并最終趨于穩定。這是因為當剛度比較小時，試樣具有較高的切向抗變形能力，剪切帶內顆粒可保證在較小的相對位移下提供與側向圍壓保持平衡的力，此時試樣總體積減小，內部顆粒重疊量增大，軸向應力較高，從而具有較高的初始彈性模量；而隨著剛度比的增加，其切向抗變形能力急劇下降，使得試樣內部調動更多的顆粒相對移動以保持與側向圍壓的平衡，導致在試驗初期產生較大側向變形。試樣總體積增加，內部顆粒重疊量變小，軸向應力下降，從而造成初始彈性模量下降。而當顆粒的切向剛度減小到一定程度時，試樣已完全調動內部顆粒以抵擋外部荷載，此時繼續增加剛度比對初始彈性模量影響不大，因此在曲線上體現為初始彈性模量隨著剛度比的增大而趨于定值。

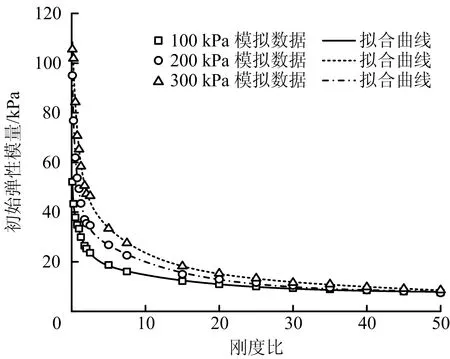
圖7 不同圍壓下初始彈性模量隨剛度比變化關系曲線

2.3 摩擦系數的影響

摩擦系數主要對土體的強度產生影響。因3種不同圍壓條件下，不同摩擦系數下的偏應力-軸應變關系曲線的規律相似，此處選取100 kPa為例進行分析，規律曲線如圖8所示，其中μ為摩擦系數。由圖8可知，摩擦系數與峰值強度呈正相關，而殘余強度會隨著摩擦系數的增大而趨于定值。

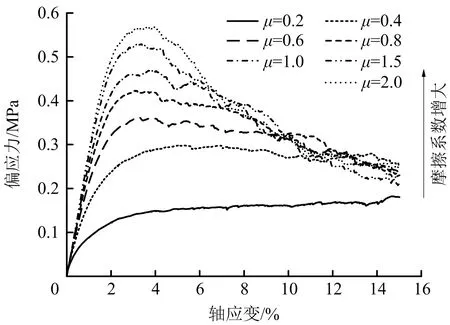
圖8 100 kPa圍壓時不同摩擦系數下的偏應力-軸應變關系曲線

隨著摩擦系數的增加，偏應力-軸應變曲線的變化可大致分為2個階段。當摩擦系數較小時，土體偏應力-軸應變曲線整體呈現出“松砂型”的應變硬化趨勢。而當摩擦系數較大時，偏應力-軸應變曲線呈現出“密砂型”的應變軟化趨勢。顯然，試樣的細觀摩擦系數和所模擬土的宏觀密實度之間存在相關性，即在同一粒徑分布下，細觀摩擦系數與土體的宏觀壓實度存在一定關系，這與文獻[14]類似。

為考察摩擦系數對試樣黏聚力的影響，繪制不同摩擦系數下強度包線及內摩擦角關系圖，如圖9所示。由圖9可知，隨著摩擦系數的增大，試樣的內摩擦角顯著增大，而增長速率隨之減小；而從強度包線明顯看出，摩擦系數的增加不會使試樣產生黏聚力。

圖9 摩擦系數對強度包線及內摩擦角的影響

2.4 抗轉動系數的影響

抗轉動系數會顯著影響土體的抗剪強度。因3種不同圍壓條件下，不同抗轉動系數下的偏應力-軸應變關系曲線的規律相似，此處選取100 Pka為例進行分析，100 kPa圍壓時不同抗轉動系數下的偏應力-軸應變關系曲線如圖10所示，其中，μr為抗轉動系數。通過對模擬結果進行對比與分析，發現抗轉動系數的取值存在作用區間，在此區間內，試樣的峰值強度和殘余強度均會隨著系數的增大而增大，呈現出整體上升的趨勢。當抗轉動系數接近閾值時，土體偏應力-軸應變曲線基本不發生變化。其主要原因是當抗轉動系數較大時，顆粒間臨界轉動阻力矩較大，此時試樣中的顆粒間的相對轉動矩未達到臨界轉動阻力矩，導致顆粒間發生的相對轉動較小，宏觀上表現為試樣強度和變形參數幾乎不隨之變化。

圖10 100 kPa圍壓時不同抗轉動系數下偏應力-軸應變關系曲線

為考察抗轉動系數對試樣黏聚力的影響，繪制不同抗轉動系數下強度包線與內摩擦角關系圖，如圖11所示。由圖11可知，抗轉動系數不會使試樣產生黏聚力，進一步驗證抗轉動模型對無黏性土的適用性。

圖11 抗轉動系數對強度包線及內摩擦角的影響

此外，抗轉動系數也對試樣的剪脹性有顯著影響。不同抗轉動系數下試樣的體應變-軸應變變化曲線如圖12所示。由圖12可知，隨著抗轉動系數的增大，試樣的體應變在加載初期的彈性階段并未產生較大的變化，即泊松比不被抗轉動系數所影響。而隨著加載不斷進行，曲線發生分化，抗轉動系數越大的試樣剪脹趨勢越強，且當抗轉動系數接近閾值時趨于穩定，也進一步證明抗轉動系數的取值存在主要作用區間這一結論。

圖12 100 kPa圍壓時不同抗轉動系數下的體應變-軸應變曲線

3 基于隨機森林回歸模型的參數權重分析

由于模型的參數間存在一定的交互作用，即多個細觀參數會對單個宏觀參數共同產生影響。而以上控制變量試驗無法精確體現出影響的權重，因此引入隨機森林機器學習法作為工具，對參數進行進一步的精細化分析。

隨機森林算法是廣泛使用于計算機領域的1種機器學習算法，其基于決策樹與bagging思想，通過建立多棵決策樹以提高預測性能，其預測值由各棵樹輸出的平均數所決定[15]。該算法具有權重分析功能，可以考察各個自變量特征的重要性。

本文基于抗轉動線性接觸模型開展300組隨機細觀參數的三軸試驗，并利用python語言sklearn庫基于隨機森林算法建立預測模型，根據文獻[16]與本文模擬結果，確定主要參數范圍，見表4。

表4 隨機參數范圍

3.1 模型建立過程

以模型的4個自有參數作為輸入層參數，以初始彈性模量、泊松比與最大偏應力3個參數作為輸出層參數，并隨機選取300組數據中的240組作為訓練集，60組作為測試集，以擬合度R2作為模型好壞評估的指標。

3.2 模型調參

隨機森林模型具有較多的模型參數，正確的參數選擇能夠減少模型過擬合并保證其具有較高的準確度和泛化性能。其中回歸樹數量n_estmators與最大樹深max_depth2個參數對模型優劣起著重要作用。采用網格搜索法找到最佳模型參數，所建立模型的優劣以擬合優度R2為考察指標，所得參數和模擬結果見表5，結果表明，訓練的模型具有較高的準確性。

表5 隨機森林模型參數與擬合度

3.3 權重分析

由于隨機森林模型存在隨機性，每次訓練均可能得到規律相同但權重系數有一定差別的結果，因此為消除其影響，用相同的模型參數訓練10 000次模型再對權重參數取平均值作為最終結果。

隨機森林輸出的宏細觀參數權重柱狀圖如圖13所示。由圖13可知，權重值越大代表影響程度越大，其總體規律與本文對比試驗結果相似。其中，抗轉動系數(0.564 72)與摩擦系數(0.427 5)顯著影響試樣的最大偏應力且前者的影響偏大；剛度比主要對泊松比(0.751)產生決定性影響，對初始彈性模量(0.201 57)起次要作用；有效模量對初始彈性模量(0.695 14)起主要作用，而對泊松比(0.193 64)起次要作用。

圖13 隨機森林輸出的宏細觀參數權重柱狀圖

4 結論

1)試樣的變形參數主要受顆粒有效模量與剛度比的影響。有效模量的增加會顯著增加試樣的初始彈性模量且增加試樣的泊松比。剛度比的增加會顯著降低試樣的初始彈性模量且增加泊松比。

2)試樣的強度參數主要受顆粒間摩擦系數與抗轉動系數的影響。摩擦系數的增加會顯著增加試樣的峰值強度而幾乎不影響試樣的殘余強度；而抗轉動系數的取值存在作用區間，當抗轉動系數處于區間內時，試樣的峰值強度與殘余強度會隨著抗轉動系數的增大而增大，而當抗轉動系數取值大于區間時，試樣的峰值強度與殘余強度將不再增加。此外，抗轉動系數與試樣的剪脹性顯著相關。

3)隨機森林可以較好地表征宏細觀參數中的影響關系。對于試樣初始彈性模量而言，主要因素的影響權重排序為有效模量(0.695 14)>剛度比(0.201 57)；對于試樣泊松比而言，主要因素的影響權重排序為剛度比(0.751)>有效模量(0.193 64)；對于試樣峰值而言，主要因素的影響權重排序為抗轉動系數(0.564 72)>摩擦系數(0.427 5)。