考慮隨機誤差的軟土基坑沉降趨勢分析及預測*

苗蘭弟，任慶國

(陜西鐵路工程職業技術學院，陜西 渭南 714000)

0 引言

為滿足市政經濟建設需求，地下空間工程開發日益發達，尤其是市政軌道工程建設。建設過程產生大量車站基坑，受施工條件限制，軟土地區基坑施工不可避免，但軟土地區土體工程性質較差，需對軟土地區基坑變形規律展開研究[1-3]。沉降監測是基坑施工變形監測必測項目，相關學者針對沉降監測開展研究：姚文龍等[4]對基坑施工過程地表沉降進行理論計算；王燦等[5]利用數值模擬分析基坑近接施工過程中地表沉降規律；基于文獻[6-7]研究成果得出，基坑變形數據誤差信息會影響基坑沉降規律，需對誤差信息分解處理；王成等[8]通過研究得出卡爾曼濾波具有較強誤差分解能力，應用于基坑誤差信息分解可行；王雪妮等[9]驗證M-K檢驗在基坑變形趨勢判斷中適用性；鐘國強等[10]驗證廣義回歸神經網絡在基坑變形預測中有效性。上述研究雖取得一定成果，但研究方法單一，且未考慮隨機誤差影響，缺乏系統性。因此，本文以蘇州4號線活力島站基坑為工程背景，利用卡爾曼濾波分解基坑沉降數據趨勢項與誤差項，采用M-K檢驗、優化廣義回歸神經網絡和差分整合移動平均自回歸模型開展基坑沉降趨勢分析及預測，以期合理掌握基坑沉降變形規律，為安全施工提供理論指導。

1 基本原理

基坑沉降監測受環境因素、人為因素擾動，變形數據存在一定誤差，使基坑沉降實測值分解為2項，即趨勢項和誤差項。其中，趨勢項代表基坑沉降真實信息，誤差項代表不確定因素造成隨機誤差。

為準確掌握基坑沉降變形規律，利用卡爾曼濾波法對趨勢項與誤差項進行分解處理。基坑沉降變形規律研究包括2個階段：階段Ⅰ利用M-K檢驗進行趨勢項發展趨勢評價；階段Ⅱ利用優化廣義回歸神經網絡(Generalized Regression Neural Network，GRNN)和差分整合移動平均自回歸模型(Arima)進行基坑沉降變形預測。通過對2個階段結果進行對比，實現基坑沉降變形規律綜合研究。

1.1 信息分解處理模型構建

卡爾曼濾波系統狀態下最優估計算法，相較于傳統小波去噪具有一定優越性，但受傳統理論基礎限制，標準型卡爾曼濾波存在發散強、抵抗力差等缺點。為此得到改進型卡爾曼濾波法，主要包括自適應型、抗差自適應型和半參數型3種。

為保證基坑沉降數據信息分解效果，將分析過程分為2個步驟：將標準型卡爾曼濾波與傳統sym、cof小波進行分解效果對比，且傳統sym、cof小波階次設定為3、5、7、9階；對比4類卡爾曼濾波分解效果，確定最優分解類型。

信息分解效果評價常用指標包括信噪比、均方根誤差等，鑒于不同評價指標原理差異，基于信噪比及均方根誤差指標，構建綜合評價指標l(k)如式(1)所示：

l(k)=l1(k)+l2(k)

(1)

式中：l1(k)、l2(k)分別為信噪比及均方根誤差指標歸一化值，l(k)值越大，分解效果相對越好；k為分解方法序號。

歸一化處理能有效避免不同評價指標單位差異影響。

1.2 發展趨勢分析模型構建

Manner-Kendall檢驗法(簡稱：M-K檢驗)是1種非參數統計方法，操作簡單、準確性高，可有效實現變形趨勢判斷分析，在基坑工程中應用廣泛。基坑沉降數據誤差信息會影響分析結果，因此，僅采用M-K檢驗對趨勢項進行發展趨勢評價。

M-K檢驗過程得到初步統計量S，如式(2)所示：

(2)

式中：Xi，Xj分別為時間節點i與j沉降值；sgn(θ)為反應函數(當θ<0時，sgn(θ)為-1；當θ>0時，sgn(θ)為1；當θ=0時，sgn(θ)為0)。

對S進行變換處理，得到M-K檢驗最終統計量Z，如式(3)所示：

(3)

式中：Var(S)=[n(n+1)(2n+5)]/18；n為樣本總數。

在檢驗水平a條件下得到對應臨界值Za，若Za0時，基坑沉降呈增加趨勢；反之，基坑沉降呈減小趨勢。

同時，由于臨界值Za與臨界水平a相關，即檢驗水平a越低，臨界值Za越大，可利用檢驗水平劃分基坑沉降變形顯著性等級，具體基坑沉降趨勢等級劃分標準見表1。

表1 基坑沉降趨勢等級劃分標準

1.3 沉降預測模型構建

基坑沉降變形數據分為趨勢項和誤差項，2者信息存在一定差異。構建相應預測模型，首先利用優化GRNN模型實現主趨勢項預測，再利用Arima模型實現殘差修正預測，具體包括以下2個過程：

1)主趨勢項預測模型構建

GRNN模型是傳統徑向基神經網絡改進形式，理論基礎更加完善，具有較強非線性預測能力，適用于基坑沉降主趨勢項預測；同時，該模型相較于傳統神經網絡模型，具有4層網絡結構，新增加和層加快收斂速度。

但GRNN模型因收斂較快，易陷入局部極值。果蠅算法(Fruit Fly Optimization Algorithm,FOA)是1種常用優化算法，全局優化能力較強，可有效優化GRNN模型。傳統FOA算法優化步長為定值，步長過大，局部搜索能力變弱；反之，全局優化不足，多種群果蠅算法(MFOA)可有效克服上述問題。因此，本文利用MFOA算法對GRNN模型進行優化，構建基坑沉降變形主趨勢項MFOA-GRNN預測模型。

2)殘差序列修正預測模型構建

MFOA-GRNN預測模型保證模型參數最優性，但受沉降數據非線性限制，難以全面刻畫基坑沉降變形主趨勢項變形規律，預測結果存在誤差。將該預測誤差與卡爾曼濾波分解出誤差項組合，構成基坑沉降變形殘差序列；為保證沉降預測精度，利用Arima模型進行殘差修正預測。

將Arima模型殘差修正結果與MFOA-GRNN模型主趨勢項預測結果疊加，即基坑沉降最終預測結果。

預測過程中，利用預測結果相對誤差均值與訓練時間進行預測效果評價，前者主要用于評價預測精度，后者主要用于評價收斂速度。

2 實例分析

2.1 工程概況

活力島站隸屬蘇州地鐵4號線，位于春申湖南側，近似沿文靈路展布；基坑外包長度199.6 m，外包寬度19.7 m，標準段開挖深度16 m，端頭加深段開挖深度18.5 m；同時，該基坑采用地下連續墻支護，并設置5道橫撐，開挖方量達6.4萬m3。

勘察結果顯示，工程區為沖積湖平原地貌，地勢相對平坦，地面標高介于2.72～4.02 m；基坑開挖范圍內主要涉及4類土層。

工程區內地表水以文靈河為主，其余為地表水網，受降雨影響較大。地下水埋深1.3～2.3 m，主要包括潛水、微承壓水和承壓水，其中潛水主要分布于土層孔隙中，年變幅約1 m，歷史最高、最低水位分別為2.63，0.21 m；微承壓水主要賦存于④1粉黏夾粉土中，水頭標高約1 m，對施工影響較大；承壓水賦存于坑底下部土層，埋深大于30 m，對施工影響較小。

2.2 沉降變形特征分析

由于工程區開挖范圍土體具軟土特征，為保證施工安全，在基坑施工過程中，進行變形監測。其中，沉降監測為必測項。在活力島站基坑施工過程中，共布設26組沉降監測，每組含3個監測點，按基坑邊垂向布設，距基坑支護結構距離分別為0，2，7 m(序號依次為1#、2#和3#)，基坑沉降監測點布置如圖1所示。

圖1 基坑沉降監測點布置

一般距基坑工程越近受擾動越大。對監測點1#沉降變形分布進行統計，如圖2所示。由圖2可知，基坑沉降變形具明顯波狀起伏，分別計算北側、南側、東側及西側沉降均值分別為13.50,14.05,16.78,17.15 mm；結合沉降監測點布設情況可知，基坑短邊向沉降變形相對偏小，長邊向中部沉降變形相對偏大，原因是基坑短邊或拐角處支護結構剛度相對較大，長邊中部處結構剛度相對較小。

圖2 1#監測點沉降變形分布

為分析沿基坑邊垂向沉降分布特征，選取沉降變形較大的4個監測點(DB-07、DB-09、DB-21和DB-23)進行統計，基坑垂向沉降分布特征如圖3所示。

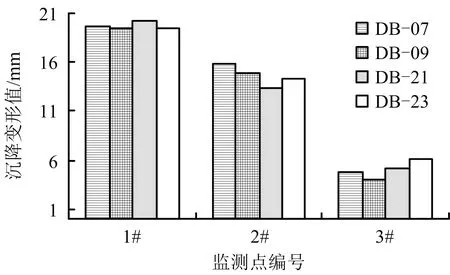
圖3 基坑垂向沉降分布特征

由圖3可知，隨距支護結構距離增加，沉降變形逐漸減小，且2#監測點與1#監測點沉降變形差值明顯小于3#監測點與2#監測點沉降變形差值。因此，建議基坑施工期間，應與周邊臨近建/構筑物保持安全距離。

在沉降監測過程中，監測頻率為2 d/次，共27個周期沉降監測成果，基坑沉降變形曲線如圖4所示。由圖4可知，4個監測點沉降變形呈持續上升趨勢。

圖4 基坑沉降變形曲線

2.3 變形數據信息分解處理

以DB-07監測點為例，進行卡爾曼濾波分解效果驗證。將標準型卡爾曼濾波與傳統小波分解效果對比分析，結果見表2。

由表2可知，傳統小波階次對分解效果影響較明顯，隨小波階次增加，分解效果逐漸變好。通過對比3類方法分解效果可知，卡爾曼濾波評價指標值最大為1.836，其次為cof小波和sym小波，說明卡爾曼濾波相對傳統小波信息分解效果更好。

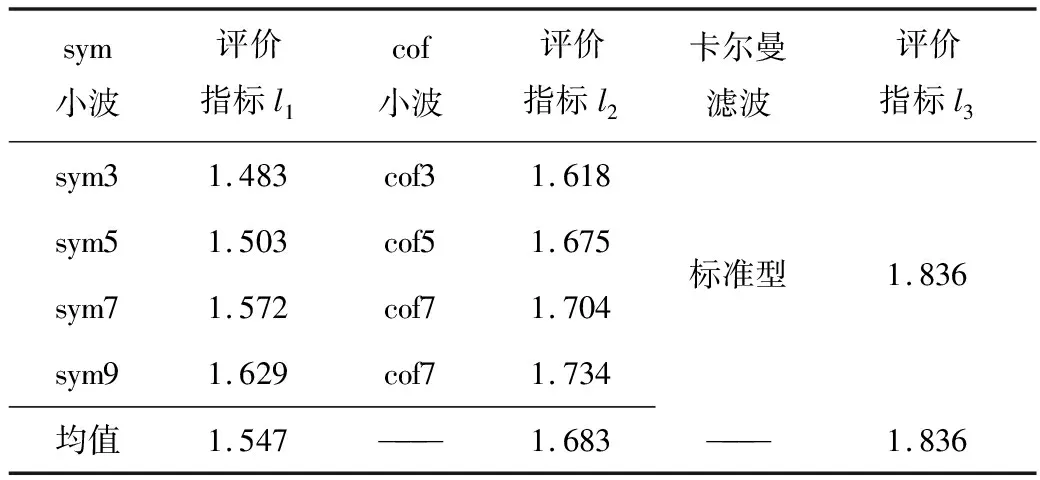
表2 卡爾曼濾波與傳統小波的分解效果對比

對多種改良型卡爾曼濾波信息分解效果對比，結果見表3。由表3可知，不同類型卡爾曼濾波分解效果差異明顯，3種改良型分解能力優于標準型，且半參數型分解效果相對最優，其次是自適應型和抗差自適應型。

表3 不同類型卡爾曼濾波的分解效果對比

綜上，半參數型卡爾曼濾波信息分解能力相對最優，將其作為基坑沉降數據信息分解方法切實可行。

2.4 沉降變形發展趨勢分析

利用M-K檢驗對基坑沉降變形趨勢項發展趨勢分析。分析過程包含整體趨勢分析和分階段趨勢分析。其中，整體趨勢分析是對所有監測數據進行M-K檢驗，以評價基坑整體發展趨勢；分階段趨勢分析將監測成果分為3個階段(每階段遞增9期監測成果)，并對每階段進行M-K檢驗，以評價基坑沉降不同階段發展趨勢。

1)整體趨勢分析。對4個監測點整體趨勢進行分析，結果見表4。由表4可知，不同監測點Z值存在一定差異，表明沉降趨勢性不同。其中，DB-07和DB-23監測點顯著性等級為Ⅱ級，顯著性程度屬顯著；DB-09和DB-21監測點顯著性等級為Ⅰ級，顯著性程度屬弱顯著。4個監測點顯著性等級雖存在一定差異，但發展趨勢均呈增加趨勢，說明整體分析條件下，基坑沉降仍會進一步增加。

表4 基坑沉降的整體趨勢分析結果

2)分階段趨勢分析。4個監測點分階段趨勢分析結果見表5。由表5可知，不同階段顯著性等級存在差異：階段2顯著性等級相對最高，即隨監測時間增加，基坑沉降顯著性呈先增加后減小趨勢。

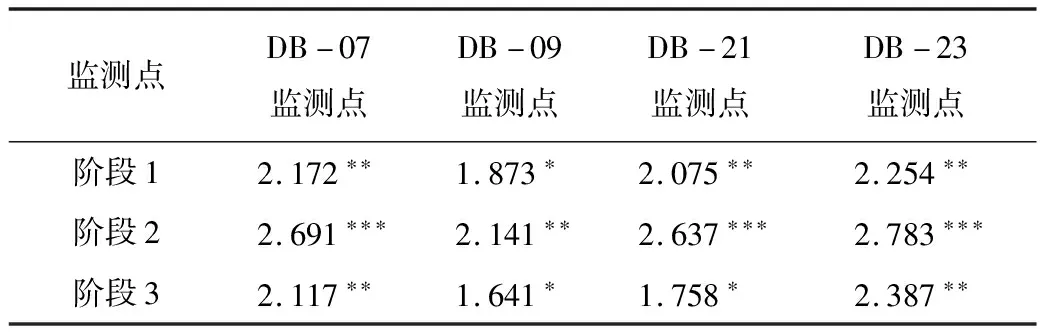
表5 基坑沉降分階段趨勢分析結果

綜上可知，活力島站基坑沉降仍具增加趨勢，但趨勢性相對減弱。

2.5 沉降變形預測分析

以DB-07監測點為例，描述不同優化階段預測效果，實現預測思路初步驗證；利用其余3個監測點預測結果，實現預測思路可靠性驗證。預測過程中，以1～22周期為訓練樣本，23～27周期為驗證樣本，外推預測周期為4期。

1)初步驗證分析。利用果蠅算法優化GRNN模型，并將FOA算法和MFOA算法優化結果進行統計，結果見表6。由表6可知，在驗證節點處，MFOA-GRNN模型相對誤差值均不同程度小于FOA-GRNN模型相對誤差值，MFOA-GRNN模型相對誤差均值和訓練時間分別為2.13%和42.21 ms，FOA-GRNN模型相對誤差均值和訓練時間分別為2.47%和47.39 ms，說明MFOA算法預測精度更高，收斂速度更快，驗證MFOA算法優越性。據MFOA-GRNN模型預測誤差均值僅為2.13%，驗證趨勢項預測思路有效性，且訓練時間相較于優化前略有增加，但影響不大，屬可接受范圍。

表6 DB-07監測點的趨勢項預測結果

利用Arima模型進行殘差修正，DB-07監測點最終預測結果見表7。由表7可知，通過殘差修正預測，DB-07監測點最大、最小相對誤差分別為2.03%和1.68%，平均相對誤差為1.80%，較殘差修正前有明顯提高，驗證Arima模型殘差修正能力；通過Arima模型殘差修正增加一定訓練時間，但僅為53.18 ms，屬可接受范圍。在外推預測結果中，DB-07監測點沉降變形仍會進一步增加，但增加速率較小。

表7 DB-07監測點最終預測結果

2)可靠性驗證分析。其余3個監測點可靠性預測結果見表8。由表8可知，3個驗證監測點平均相對誤差間于1.80%～1.90%，與DB-07監測點預測精度基本一致，說明本文預測模型具有較強穩定性，且訓練時間均小于60 ms，屬可接受范圍。

表8 可靠性驗證預測結果

對比3個監測點外推預測結果可知，3者沉降變形均會進一步增加，但增加速率均明顯降低，與DB-07監測點外推預測結果一致，充分說明本文通過預測得出沉降趨勢判斷結果準確性較高。

3 結論

1)基坑沉降變形數據含有一定誤差信息，給變形規律研究帶來一定影響；相較傳統小波，卡爾曼濾波對趨勢項及誤差項分解效果更佳。

2)M-K檢驗能準確實現基坑沉降趨勢分析，隨監測時間增加，基坑沉降呈持續增加趨勢，但顯著性呈先增加后減小趨勢，基坑沉降增加趨勢逐漸減弱。

3)沉降預測模型構建過程中，對模型參數進行優化處理，保證參數最優性。本文預測思路精度較高，平均相對誤差均小于2%，驗證預測思路在基坑沉降預測中有效性；由外推預測可知，沉降變形會進一步增加，但增加速率明顯降低，與發展趨勢分析結果一致。