城市供水管網漏損動態預測的Bootstrap-Lee-Carter模型*

王 威，叢 旭，武佳佳，馬東輝

(北京工業大學 城市建設學部，北京 100124)

0 引言

為減少管網失效事件發生，提高城市供水管網韌性，諸多學者在對城市供水管網爆管率，漏點率以及剩余壽命進行大量預測工作，對城市安全具有重大意義。

管道破損的影響因素較多，Barton等[1]將其歸納為3大類：管道本身性質；環境因素；運行因素。

王圃等[2]將方差—協方差優選組合模型應用于對給水管網年漏損件數的預測并進行實例分析，結果表明組合模型具有較高的預測精度；邱云龍[3]針對給水管網漏損特點，用方差-協方差優選組合模型將灰色GM(1,1)模型、二次指數平滑模型、自回歸移動平均模型應用于漏損頻率的預測，提高單個模型的預測精度；王麗娟等[4]在此基礎上結合漏點數的季節性周期特點，建立基于差分自回歸移動平均模型的管網漏損預測模型。

基于管道自身性質的漏損模型預測方面，Kang等[5]根據GRA的主要程序，對城市供水管網基本滲漏數據進行處理，結果反映與滲漏有較大關系的前3個因素為管徑、管道壓力以及深度；包涵等[6]同樣利用灰色模型對管道漏損率進行預測，得出使用等維灰色模型相比傳統灰色模型和無偏灰色模型進行供水管網漏損率預測效果更好；王志紅等[7]針對城市管網漏損率數據的非線性和隨機波動性特點，建立以馬爾可夫鏈修正灰色GM(1,1)的預測模型，比較分析灰色和灰色馬可夫鏈預測結果，指出經馬爾可夫鏈修正后的模型預測精度更高。

除了以上幾種預測方法，國內外學者還從神經網絡理論出發在管道漏損率的預測中進行應用分析。Dongwoo等[8]采用主成分分析(PCA)和人工神經網絡(ANN)用于估計配水管網中的漏水量，并通過Z評分法獲得標準化數據，設計并證明PCA-ANN方法比單個ANN模擬更準確地估計泄漏率；邵圓媛[9]在常規BP神經網絡模型基礎上，結合平行拓撲結構和最小均方誤差識別模式，構建單因素的嵌套GMS神經網絡模型用來進行管網的漏損預測；汪健[10]在人工神經網絡理論基礎上，通過對小波變化的研究，建立小波神經網絡模型對供水管網的壓力及管道進行預測研究。

綜上，國內外學者目前針對供水管網漏損方面均進行了卓有成效的研究，但是在相關討論過程中，目前關于管網漏損率的研究方法大多數停留在靜態分析階段，劉曉然等[11]應用動態分級方法對管網漏損分類分級控制，但并無預測由于時變因素對管網漏損率的影響，所以本文在Lee-Carter模型[12]的基礎上結合曾燕等[13]選用的Bootstrap方法，充分考慮Lee-Carter模型所有參數的變動性，對昆明市某供水管網的漏點率進行動態分析，以便彌補靜態分析模型的不足。

1 供水片區管網概況

基于前期調研資料[14]，截止到2016年，昆明市某片區供水管網約413 km，2016年平均日供水量約1.46×104m3，供水面積約106 km2，并供約36.2萬人口使用。不同管徑和管材管道占比統計如表1所示，不同管材管道占比統計如表2所示。

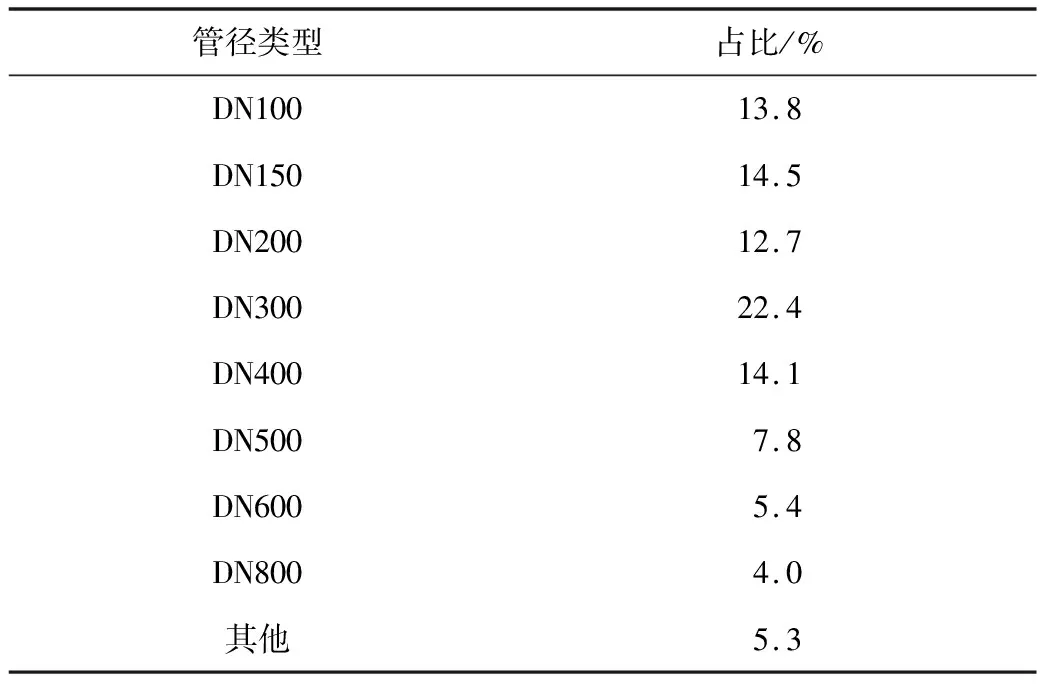
表1 不同管徑管道統計情況

表2 不同管材管道統計情況

2 Lee-Carter模型動態分析及其參數估計

2.1 模型簡介

以供水管網的管齡時間作為影響管道漏點率的主要影響因素，Lee-Carter模型如式(1)所示:

lnmx,t=ax+bxkt+εx,t

(1)

式中：mx,t為t年管徑/管材為x的管道漏點率；kt為依賴于時間t的參數；ax為依賴于管徑/管材的參數；bx為各管徑/管材漏點率對kt的敏感度；εx,t為誤差項。

(2)

式中：c為任意常數。

對模型參數進行歸一化處理，如式(3)所示：

(3)

式中：t為年份；T為年份總數；x為管徑或管材。

Lee-Carter模型預測供水管網漏損預測實現步驟：1)通過往年漏點率數據估計參數ax，bx，kt；2)通過ARIMA方法得到kt在未來的預測值；3)將kt及ax,bx代入模型，以獲得漏點率的預測值。

2.2 參數估計

1)最小二乘法(OLS)

基于Lee-Carter模型的假設，如式(4)所示：

(4)

將式(1)兩邊對管徑/管材x進行求和，如式(5)所示：

(5)

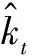
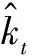
(6)

2)加權最小二乘法(WLS)

(7)

式中：dx,t為管道漏點數。

2.3 數據與擬合結果

采用OLS和WLS對該片區供水管網數據分析，可得不同管徑管道的Lee-Carter模型參數的估計值，如圖1所示。不同管材管道的Lee-Carter模型參數的估計值如圖2所示。kt值整體上變化幅度較小；ax代表管道的中心漏點率，隨著管徑增大漏點率減小；從bx的波動可以看出，小管徑管道對時間因子的敏感度較低，大管徑管道對時間更為敏感。

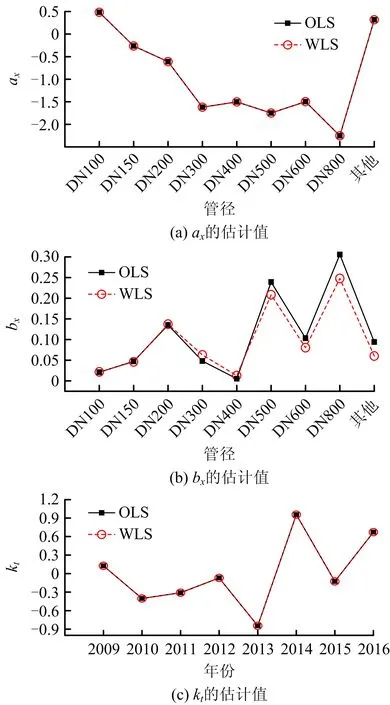
圖1 不同管徑管道經典模型的參數估計值

針對球墨鑄鐵管(DIP)、灰口鑄鐵管(GCIP)、鋼管(SP)、PE管(PEP)和水泥管(CP)進行模型參數估計，由圖2可知，2種估計方法得到的管材kt值整體上變化幅度比較小；ax的參數值反映出，DIP的管道漏點率較低，其余5種管材類型的管道均具有較高的漏點率；DIP，PEP和CP受時間因子影響較小，而GCIP和SP受時間因子影響較大。

圖2 不同管材管道經典模型的參數估計值

在2種參數估計方法中，OLS假設殘差獨立同分布；WLS假設殘差獨立，但方差與管道漏點數有關。為檢驗2種方法的殘差是否滿足各自的殘差假設，可根據參數估計時做的分布假設對2種方法殘差進行修正。若殘差的分布假設成立，則修正后的殘差應具有明顯的獨立同分布性。因此修正后殘差的獨立同分布性質可用來判別這2種估計方法的優劣。

根據式(1)可知，OLS估計的殘差假設為獨立同分布，因此不用對殘差進行修正，如式(8)所示：

(8)

WLS的殘差平方以管道漏點數作為權重，因此定義其修正后的殘差，如式(9)所示：

(9)

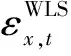
利用MATLAB編程，可得到不同管徑管道的殘差等高線圖如圖3所示，不同管材管道的殘差等高線圖如圖4所示。從圖3中管徑的殘差等高線圖中可以看出OLS和WLS均具有一定的聚集特性，而圖4中管材的殘差等高線圖都表現出了較好的隨機性。本文采用Levene方差齊性檢驗方法[15]對其進行分析，結果如表3所示。

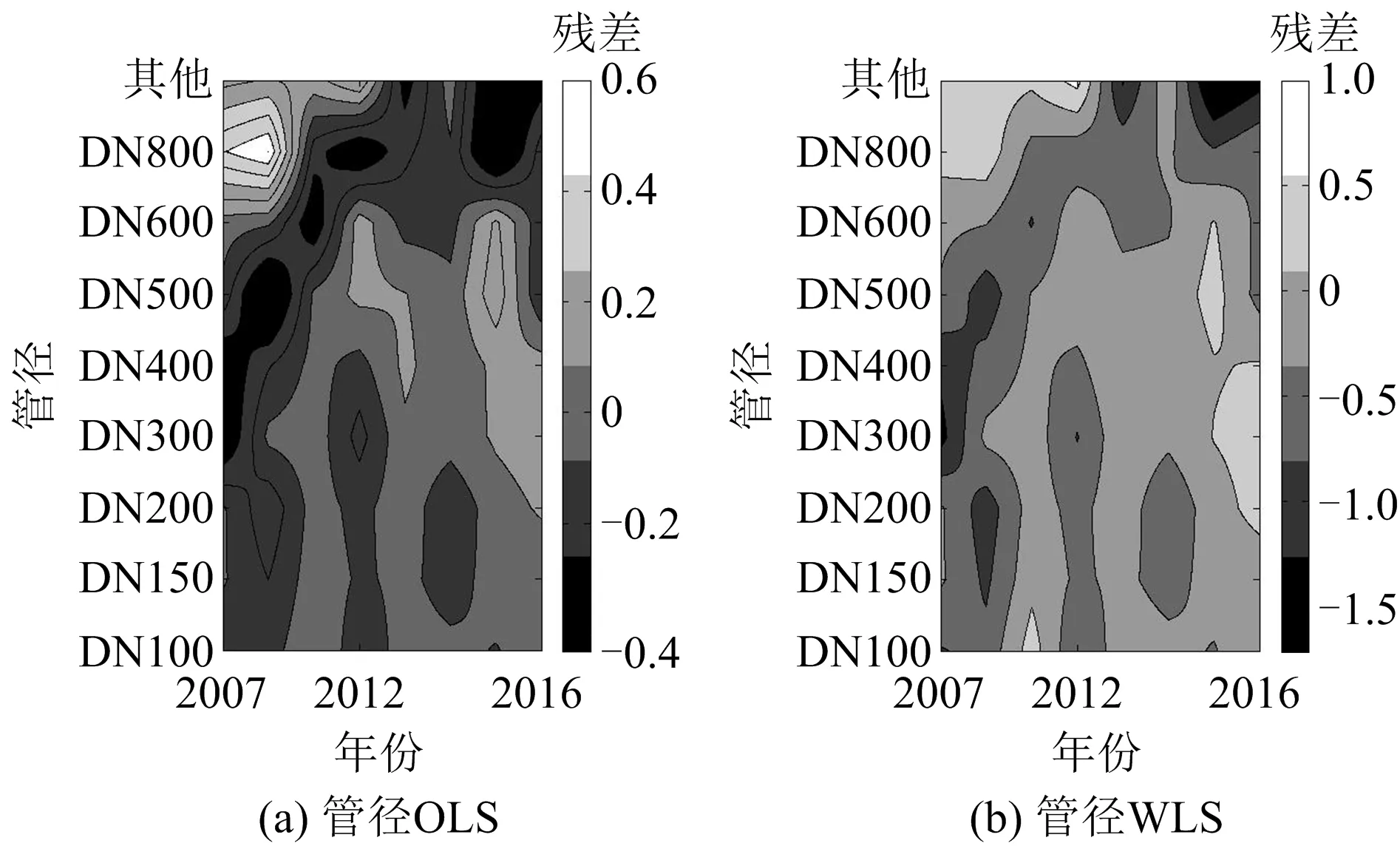
圖3 不同管徑管道的2種參數估計方法的殘差等高線

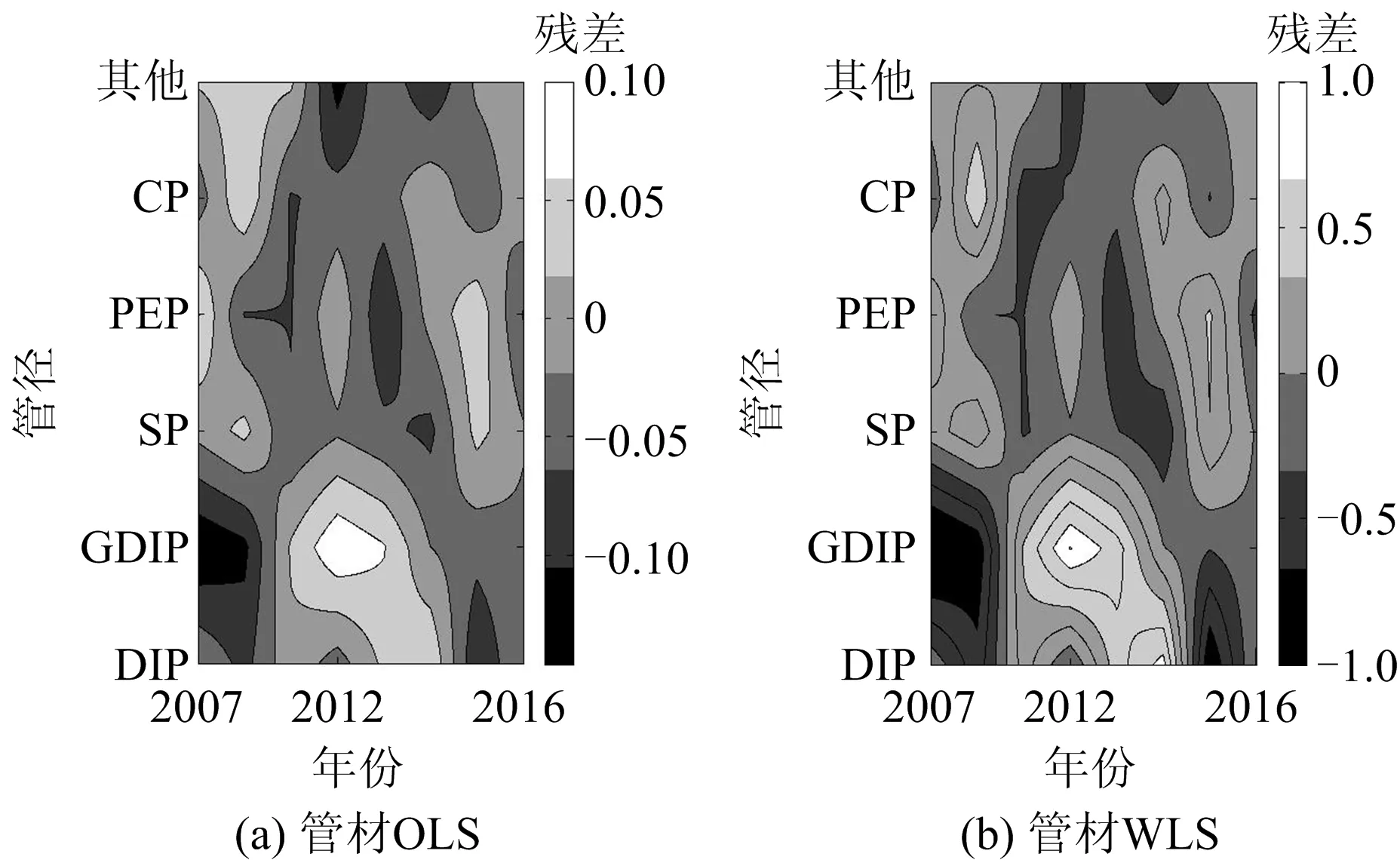
圖4 不同管材管道的2種參數估計方法的殘差等高線

基于Levene檢驗的參數值如表3所示。可知，無論按照管徑類別或管材類別，還是按照年齡，F>P，即第1列都大于最后1列，說明接收H0，不接受H1，不同方差齊性，各個樣本方差不相同。考慮時間因子，WLS的p值更大，結合殘差等高線圖，綜合考慮WLS作為參數的估計方法更優。

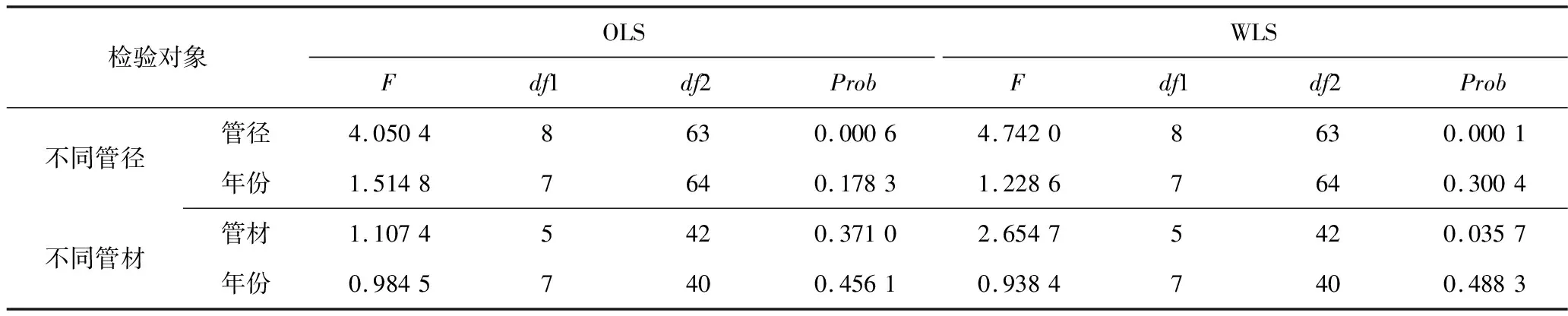
表3 基于Levene檢驗參數值

3 經典Lee-Carter模型預測管道漏點率

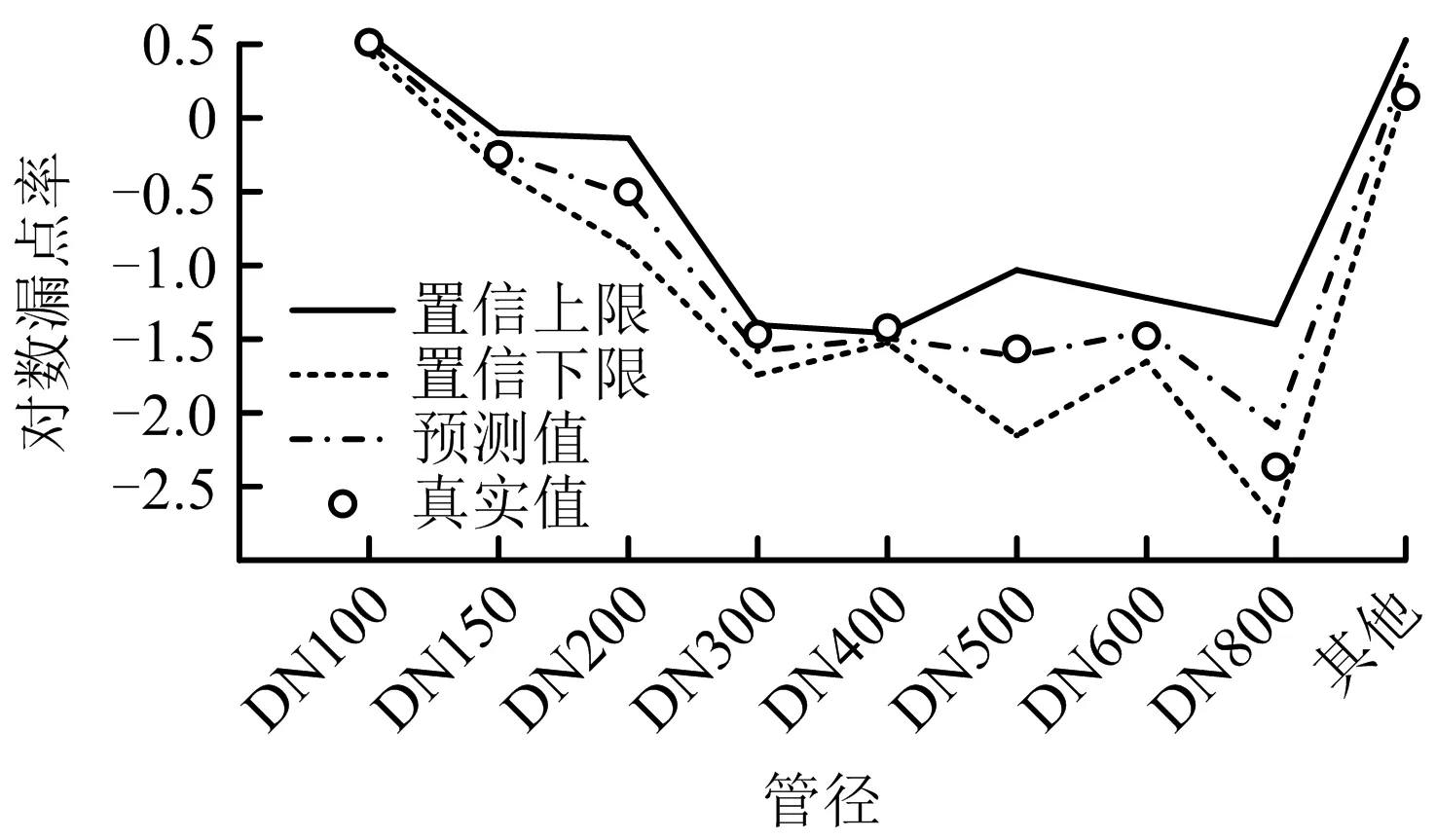
圖5 2017年不同管徑管道漏點率預測值置信區間

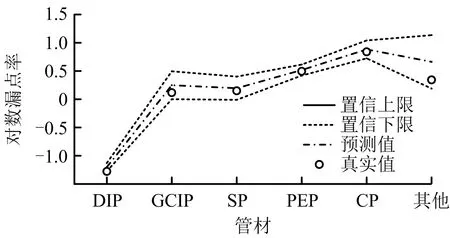
圖6 2017年不同管材漏點率預測值置信區間

由圖5和圖6可知，供水管道漏點率預測值的置信區間并不太準確，原因在于傳統的Lee-Carter模型沒有考慮其他2個參數ax，bx的變動性。而Lee-Carter模型不能通過傳統的檢驗方法對參數進行檢驗，其參數的分布不能由已知的分布函數進行描述，因此可結合Bootstrap方法對模型參數進行估計，并計算參數及漏點率的置信區間。

4 結合Bootstrap方法預測漏點率

以傳統Lee-Carter模型作為漏點率預測模型，基于Bootstrap方法計算參數置信區間的穩健性，同時在考慮所有參數變動性的基礎上預測未來漏點率的置信區間。具體實現步驟如下[13]：

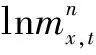
(10)

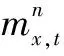
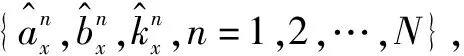
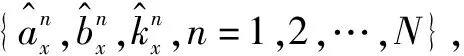
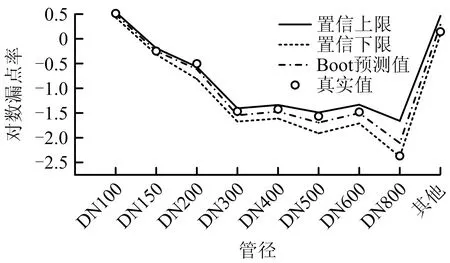
圖7 2017年不同管徑管道Bootstrap漏點率預測值置信區間

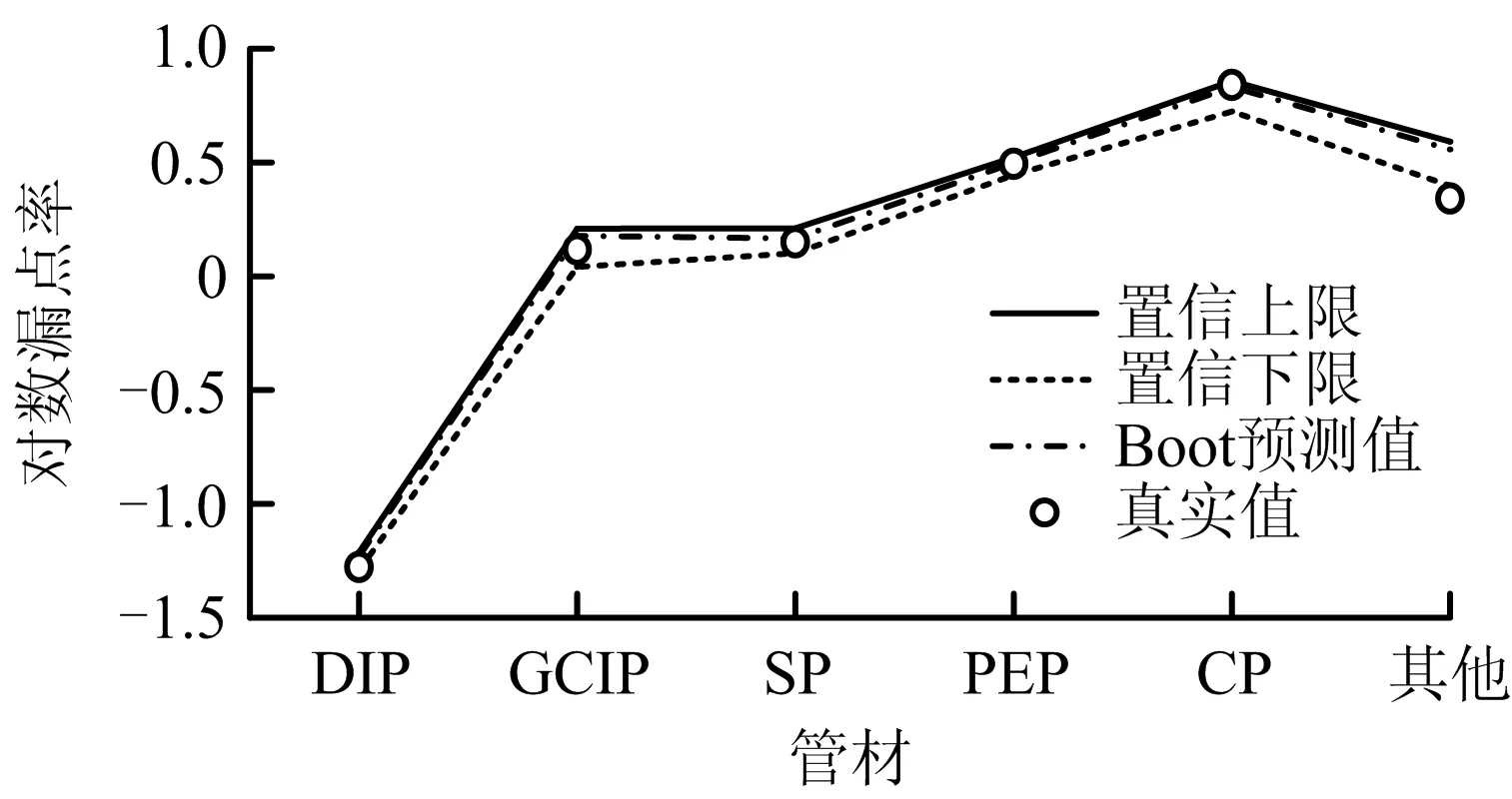
圖8 2017年不同管材管道Bootstrap漏點率預測值置信區間

將2017年不同管徑以及不同管材的管道Bootstrap預測的漏點率預測與實際的漏點率進行對比，誤差統計如表4所示。

由表4可知，DN800的管道的預測值和實際值之間誤差較大，其余管徑類型誤差較小，這是由于大管徑管道實際漏點率較低，計算相對誤差時作為分母較小，導致誤差增大，但就漏點率本身而言，預測值與實際值接近。對于不同管材的管道，計算結果顯示其他管材類型的管道誤差稍高，主要考慮到種類較多，因而漏點數的累積值較大，但預測值與實際值接近。

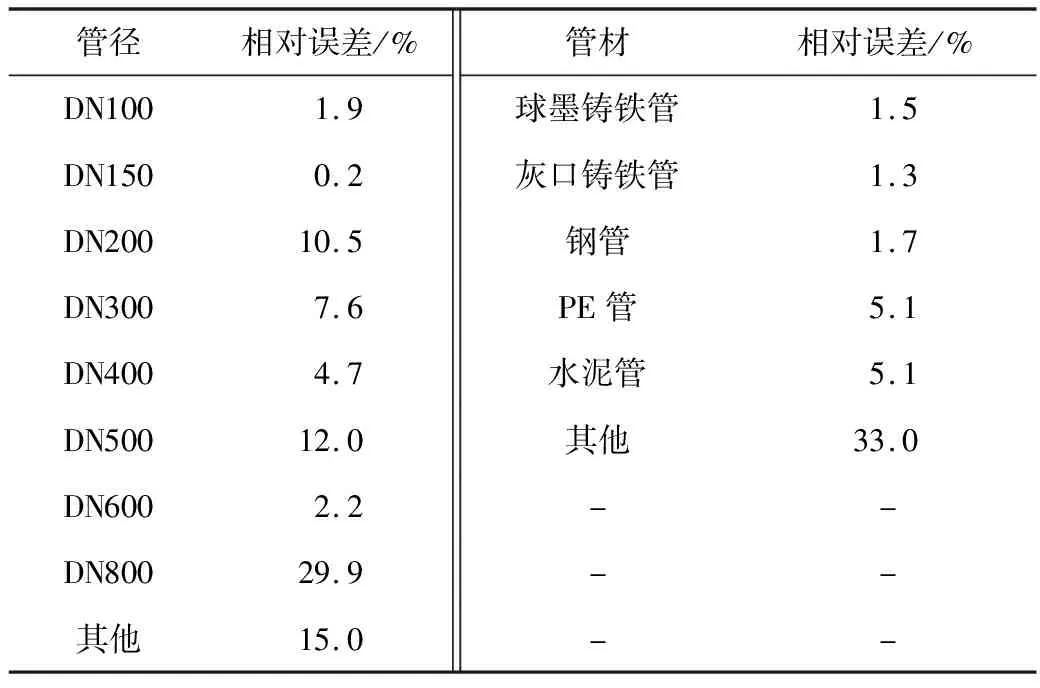
表4 2017年的Bootstrap漏點率預測值誤差統計

綜上，結合Bootstrap方法的Lee-Carter模型預測管道漏點率在精度上有較大提高，擬合效果貼近實際情況。

5 結論

1)基于Lee-Carter模型對昆明市某供水片區的管道漏點率進行擬合與預測，分析得到加權最小二乘法的殘差具有較好的獨立同分布性質。結果表明，利用Bootstrap方法預測的管道漏點率置信區間能夠包含真實的漏點率，具有較高的精度。

2)從分析結果可以得到影響管道剩余壽命的2個危險因子——管齡和管徑：管道的年限越長，管徑越小，管道剩余壽命愈短，即管道的漏損率越高。在城市供水管網系統中，為避免爆管事故的頻繁發生，需要采取針對性措施降低管道的滲漏風險，延長管道經濟剩余壽命。