勻變速荷載作用下Vlazov地基上梁的動力響應(yīng)分析

方昊，劉洋，鄭俊杰

(華中科技大學(xué) 巖土與地下工程研究所，湖北 武漢 430074)

運(yùn)動荷載作用下道路路面的動力響應(yīng)問題一直以來受到學(xué)者們的關(guān)注，道路路面結(jié)構(gòu)通常被視為置于彈性或黏彈性地基上的梁或板。Kim[1-2]考慮了板內(nèi)應(yīng)力以及板底剪切阻尼的影響，對黏彈性地基上板的動力響應(yīng)進(jìn)行了分析；Huang等[3]采用有限條分法研究了移動荷載作用下黏彈性地基上對邊簡支板的動力響應(yīng)；姚海林等[4]利用Fourier變換的方法，研究了多輪荷載作用下黏彈性Winkler地基上正交各向異性薄板的動撓度；王春玲等[5]利用積分變換法，得出了移動荷載作用下彈性半空間地基上矩形薄板的動力響應(yīng)解析解；顏可珍等[6]研究了在移動荷載作用下的Vlazov 地基上無限長梁的動力響應(yīng)。以上研究都將移動荷載假設(shè)成為勻速荷載，實際上，車輛在行駛過程中存在大量變速的情況，例如啟動、超車以及剎車，因此將移動荷載假設(shè)成變速荷載更為合理。

目前，學(xué)者們針對變速荷載下道路路面的動力響應(yīng)做了一些研究，但是非常有限。Beskou等[7]和Michaltsos[8]利用振型疊加以及Duhamel積分的方法，對勻變速荷載作用下黏彈性地基上兩端簡支梁的動力響應(yīng)進(jìn)行了分析；Huang等[9]利用有限條分法研究了黏彈性地基上對邊簡支板的動力響應(yīng)；Suziki[10]對Winkler地基上有限長梁的動撓度進(jìn)行了分析。上述都將地基簡化成黏彈性Winkler地基，但是Winkler地基模型過于簡化，不能反映土體的性質(zhì)。學(xué)者們?yōu)榱烁倪M(jìn)該模型的缺陷，研究了一系列雙參數(shù)地基模型。Vlazov地基就是這類模型中具有代表意義的一種。Nogami等[11-12]和高廣運(yùn)等[13-14]進(jìn)一步得到了修正的Vlazov地基模型。而勻變速荷載作用下Vlazov地基上梁的動力響應(yīng)還未見報道。

本文在已有研究的基礎(chǔ)上，采用一種Fourier變換與有限差分法相結(jié)合的方法，并利用數(shù)值積分，得出了勻變速荷載作用下Vlazov地基上梁的動撓度數(shù)值結(jié)果。利用數(shù)值結(jié)果，進(jìn)一步分析了荷載加速、減速和初速度對梁的動態(tài)撓度的影響。

1 控制方程及求解

如圖1所示，假設(shè)路面梁和地基完全接觸，位移連續(xù)且不考慮接觸面上的剪切應(yīng)力，根據(jù)Euler-Bernoulli梁和Vlazov地基理論，Vlazov地基上梁的動力控制方程可寫為[6]：

圖1 Vlazov均質(zhì)地基上梁模型

(1)

式中：EI為梁的抗彎剛度;W為梁的位移;p為施加在梁上的荷載。對于非均質(zhì)地基，假設(shè)彈性模量呈線性變化，且彈性層頂面的彈性模量為E1，彈性層底面的彈性模量為E2，則：

(2)

彈性層模量可寫為：

(3)

式中：Es和νs分別表示彈性層的彈性模量和泊松比；ρs表示彈性層的密度；H表示彈性層的厚度；d、ρ和h分別為梁的寬度、密度和厚度。對于均質(zhì)地基，則有E1=E2=Es。

邊界條件為：

(4)

定義對x的Fourier變換為：

(5)

其Fourier逆變換為:

(6)

對式(1)中的x進(jìn)行Fourier變換，可得到：

(7)

荷載可表示為：

p(x,t)=FdH[l2-(x-xc)2]

(8)

式中:

(9)

式中：F、2l、xc、x0、v、a依次表示線荷載的荷載大小、荷載寬度、任意時刻荷載位置的中心坐標(biāo)、初始時刻荷載中心坐標(biāo)、荷載速度以及荷載的加速度;H[·]為Heaviside函數(shù)。對荷載進(jìn)行Fourier變換，可得到：

(10)

利用有限差分法，則對于時間的二階微分可寫為：

(11)

tj=Δt(j-1)

(12)

將式(11)代入式(7),可得：

(13)

式中：

(14)

(15)

采用移動坐標(biāo)系的方法，可得出勻速荷載作用下的動力響應(yīng)的穩(wěn)態(tài)解[6]。本文采用同樣的方法，求出Vlazov地基上梁的動力響應(yīng)穩(wěn)態(tài)解，并將該穩(wěn)態(tài)解作為勻變速荷載作用下Vlazov地基上梁的動力響應(yīng)的初始條件。

引入移動坐標(biāo)系，對于任一勻速線荷載作用下的動力響應(yīng)，令X=x-x0-vt，則方程(1)可以簡化為：

(16)

定義對X的Fourier變換為：

(17)

其Fourier逆變換為:

(18)

同樣地，對X進(jìn)行Fourier變換，則式(1)可寫為：

(19)

其中：

(20)

可以得出：

(21)

對比式(6)和式(18)，由于：

W(x,t)=W(X)

(22)

可以得到：

(23)

(24)

對于第1個時間步和第2個時間步，即j=1,2的情況，將t=0，Δt代入式(24)，可得出:

(25)

將式(25)代入式(13)，作為式(13)的初始條件，并利用Fourier逆變換，就可得到勻變速荷載作用下Vlazov地基上梁的動力響應(yīng)：

(26)

2 數(shù)值驗證

為了驗證本文方法的正確性，假設(shè)荷載加速度為0，則可退化成文獻(xiàn)[6]中勻速線荷載的情況。取該文獻(xiàn)中的參數(shù)：地基土的質(zhì)量密度ρs=1 550 kg/m3，地基土的泊松比νs=0.3，地基土層厚度H=3 m，地基土的彈性模量Es=2.69×107N/m2，梁的彈性模量E=3.1×109N/m2，梁的截面是矩形截面，其中梁的寬度為d=0.3 m，梁的厚度為h=0.3 m，梁的質(zhì)量密度為ρ=2 450 kg/m3，初始時刻荷載的中心坐標(biāo)為x0=0，荷載強(qiáng)度F=3 333 N/m2，線荷載分布寬度2l=0.3 m。圖2表示不同荷載速度作用下板撓度沿x軸的分布情況。本文的計算結(jié)果與顏可珍等[6]的計算結(jié)果吻合得很好，說明本文的方法正確可行。

圖2 本文結(jié)果與文獻(xiàn)[6]結(jié)果的對比

3 數(shù)值分析

荷載速度、地基土的模量以及地基土層的厚度對板的動力響應(yīng)的影響已經(jīng)在文獻(xiàn)中有了詳細(xì)的討論。本文主要討論單軸勻變速荷載作用下加速度對Vlazov地基上梁的動撓度的影響。采用文獻(xiàn)[6]中的參數(shù)進(jìn)行數(shù)值分析。

3.1 不同初速度下加速對梁動撓度的影響

圖3為線荷載以不同的初速度和相同加速度a=3 m/s2運(yùn)動至xc=0,250, 500, 750 m處時，Vlazov地基上梁在靠近荷載中心的位置的動撓度曲線。從圖中可看出，撓度峰值發(fā)生在荷載中心，且隨著運(yùn)動距離xc的增加，動撓度峰值增加，振動更加劇烈。

圖3 加速荷載運(yùn)動至不同位置時梁在x方向的動撓度曲線

圖4表示線荷載在初速度分別為v=0,30, 60 m/s，加速度均為a=0,1, 2, 3 m/s2時，從坐標(biāo)原點沿x軸正方向運(yùn)動的過程中，梁上在x方向不同位置對應(yīng)的動撓度峰值圖像。從圖中可看出，當(dāng)加速度大于0時，動撓度峰值隨著x的增加而增加，說明勻變速狀態(tài)下的動力響應(yīng)是非穩(wěn)態(tài)響應(yīng)，且加速度越大，增加幅度越大。

對比圖4(a)、(b)、(c)，可以看出，當(dāng)初速度為v=0時，梁的撓度幅值隨著距離x的增加呈線性增加的趨勢，最大增幅達(dá)到6.448 μm，增加約23.412%；當(dāng)v=30 m/s，梁的撓度幅值隨著距離x的增加呈線性增加的趨勢，最大增幅達(dá)到7.384 μm，增加約25.874%；而當(dāng)初速度為v=60 m/s，且加速度為a=3 m/s2時，梁的撓度幅值隨著距離x的增加呈非線性增加的趨勢，最大增幅達(dá)到12.250 μm，增加約37.879%。說明初速度越大，隨著距離x的增加，動撓度增加幅度越大，加速度對于動撓度的影響越大。文獻(xiàn)[6]中的研究成果表明：速度越大，Vlazov地基上梁的動撓度響應(yīng)越大，且速度越大，速度的增加對梁的動撓度影響越大。由此可以分析，當(dāng)初速度一定時，加速度越大，到達(dá)位置x處的速度就越大，Vlazov地基上梁的非穩(wěn)態(tài)動撓度響應(yīng)就越大，且初速度越大，加速度對梁的動撓度影響越大。由此可見，加速度對于動撓度的影響是不可忽略的。

圖4 加速荷載作用下梁的撓度峰值沿x方向的分布

3.2 不同初速度下減速對梁動撓度的影響

圖5表示線荷載以不同的初速度和相同加速度a=-3 m/s2運(yùn)動至xc=0, 50, 100 m處時，Vlazov地基上梁在不同位置的動撓度曲線。從圖5中可看出，撓度峰值發(fā)生在荷載中心，且隨著運(yùn)動距離xc的增加，動撓度峰值減小，振動更加平緩。

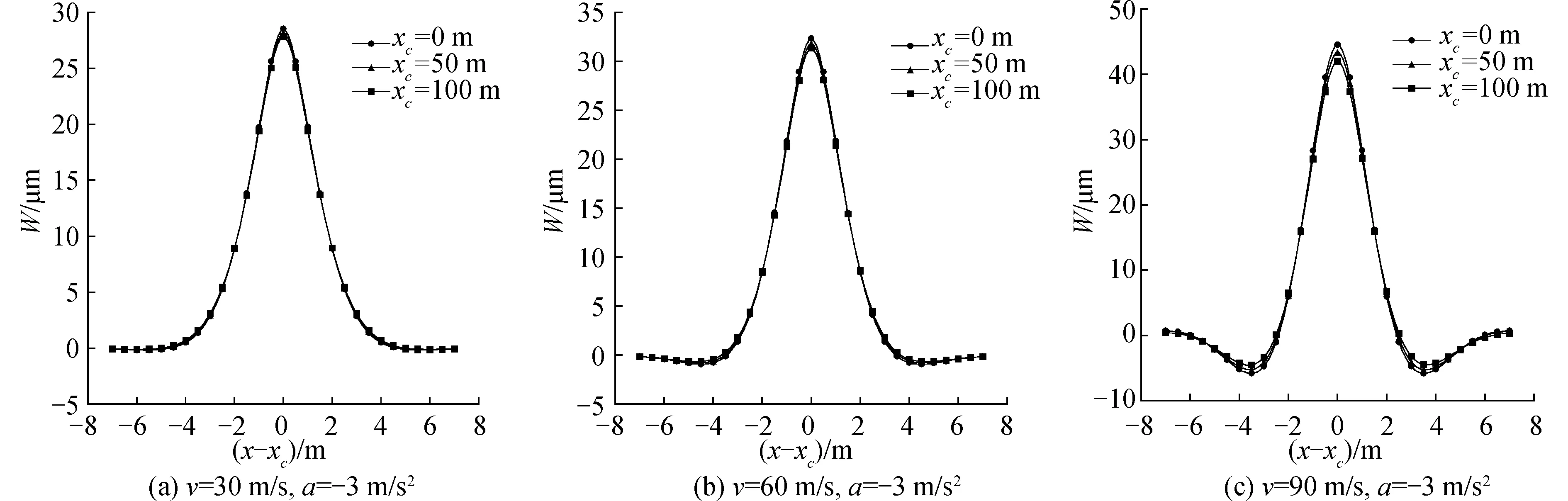
圖5 減速荷載運(yùn)動至不同位置時梁在x方向的動撓度曲線

圖6表示線荷載在初速度分別為v=30, 60, 90 m/s,加速度均為a=-1,-2,-3 m/s2時，從x=0運(yùn)動至不同位置時，梁上不同x位置對應(yīng)的動撓度峰值圖像。由圖可看出，隨著距離x的增加，撓度最大值減小，且減速越大，減小幅度越大。

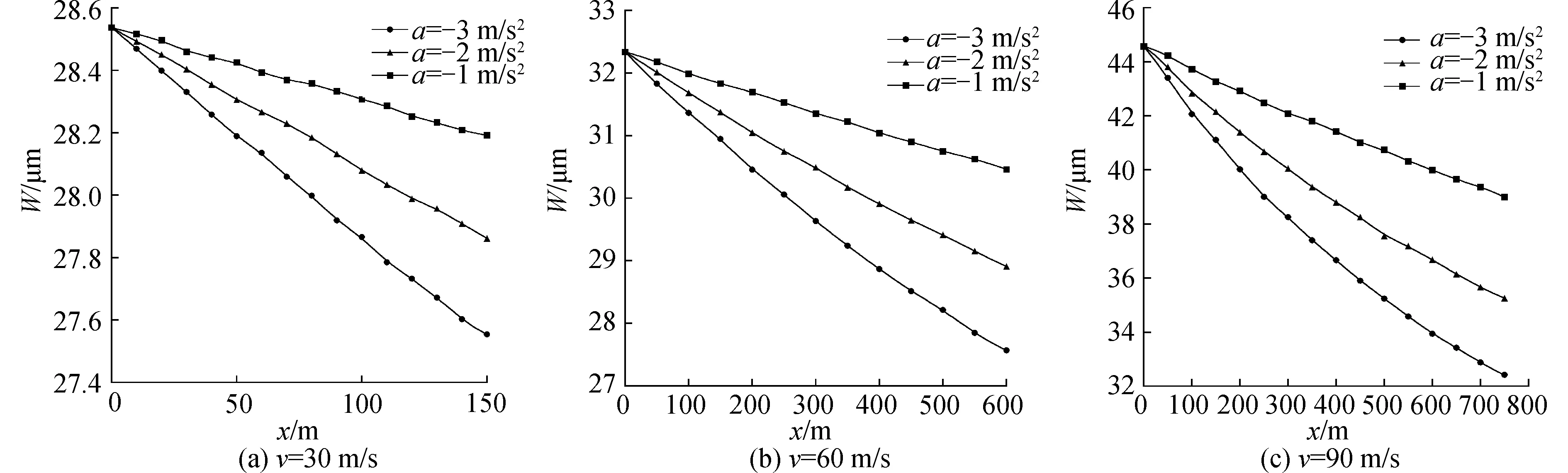
圖6 減速荷載作用下梁的撓度峰值沿x方向的分布

對比圖6(a)、圖6(b)和圖6(c)當(dāng)初速度為v=30 m/s時，梁撓度的最大減幅達(dá)到0.672×10-6m，減少約2.355%；v=60 m/s時，梁撓度的最大減幅達(dá)到0.977×10-6m，減少約3.021%，且梁的撓度最大值隨著距離x的增加呈線性減小的趨勢；當(dāng)v=90 m/s，且加速度為a=-3 m/s2時，梁撓度的最大減幅達(dá)到2.512×10-6m，減少約5.636%，梁的撓度最大值隨著距離x的增加呈非線性減小的趨勢，說明初速度越大，動撓度峰值減小幅度越大，減速對于動撓度的影響越大。同樣地可以分析出，當(dāng)初速度一定時，減速越大，到達(dá)位置x處的速度就越小，Vlazov地基上梁的非穩(wěn)態(tài)動撓度響應(yīng)就越小，且初速度越小，減速對梁的動撓度影響越小。由此可見，減速對于動撓度的影響是不可忽略的。

3.3 梁動撓度的參數(shù)敏感性分析

本文主要對荷載初速度、加速和減速進(jìn)行敏感性分析。從圖7和圖8可以看出，載荷在運(yùn)動過程中，對于梁上的不同位置x，梁的動撓度都對梁的初速度敏感；從圖9可以看出，當(dāng)x≤50 m，即靠近荷載初始位置時，梁的動撓度隨加速度的變化很小，即對加速度不敏感，對比a=0的情況，梁的撓度峰值增加最大也只有1.657%，但在遠(yuǎn)離荷載初始位置處，即x較大時，梁的動撓度對加速度敏感，且對比荷載勻速運(yùn)動的情況，a=3 m/s2情況下梁的撓度峰值最大可增加26.736%，a=-3 m/s2情況下梁的撓度峰值最大可減少14.808%，說明梁的動撓度響應(yīng)對加速更敏感。

圖7 減速荷載以不同初速度作用下梁的撓度峰值

4 結(jié)論

1)隨著運(yùn)動距離的增加，加速荷載作用下的梁的振動幅值越大，振動更加劇烈，減速荷載作用下的梁的振動幅度越小，振動越平緩，說明梁的動撓度與荷載的運(yùn)動距離有關(guān)，且加速荷載相較于減速荷載對梁的動撓度影響更大。

2)勻變速荷載的初速度對彈性地基上梁的動撓度影響非常明顯，初速度越大，梁的動撓度越大，加速或減速對梁的動撓度的影響越大，即加速越大，梁的動撓度增加的幅度越大；減速越大，梁的動撓度減小的幅度越大。

3)彈性地基上梁的動撓度峰值對荷載加速度的敏感程度與距離荷載初始位置的距離x有關(guān)，當(dāng)x≤50 m，即靠近荷載初始位置時，梁的動撓度峰值對加速度不敏感，但是在遠(yuǎn)離荷載初始位置處，即x較大時，梁的動撓度對加速度敏感，且對加速更敏感。在x=600 m處，對比勻速運(yùn)動的情況，a=3 m/s2情況下梁的撓度峰值最大可增加26.736%，因此在工程設(shè)計過程中，將荷載考慮成勻變速荷載更合理，且應(yīng)當(dāng)精確測量荷載的加速度，以減少計算誤差。