面向VR放置任務的自然手勢交互時間的預測

顏寶明，潘偉杰，呂 健，王 毅，趙澤宇

（貴州大學現代制造技術教育部重點實驗室，貴州 貴陽 550025）

隨著交互技術的快速發展，自然交互（natural interaction，NI）作為一種新的體驗技術被廣泛應用于虛擬現實（virtual reality，VR）環境中［1］。用戶在日常生活中與真實世界的互動可以轉化為人與機器之間的交互［2］。在人機自然交互中，用戶在人機系統中的輸入方式分為手勢行為輸入和其他肢體行為輸入。傳統的鼠標、鍵盤等交互設備僅適用于二維交互，無法滿足VR 環境中人機交互對交互設備和交互方法的新要求［3］。在三維交互中，Oculus手柄、HTC Vive手柄等設備［4-6］結合頭戴顯示器和定位系統，根據用戶發出的指令，在執行VR 交互任務時具有效率高、延遲低等特點。然而，在執行VR 交互任務時，雷金樹［5］發現相比于通過手柄交互，用戶更傾向于通過自然手勢直接與虛擬對象交互。隨著VR 技術的快速發展，一種更加接近真實人手操作的人機交互方式開始出現。梁民倉等［7］以Leap Motion控制器和Kinect控制器等為交互設備，通過機器視覺技術和圖像處理技術獲取圖像和視頻，達到手勢特征識別和重建的目的［7］。

為了在VR 環境中準確模擬用戶的放置任務并預測自然手勢的交互時間，筆者提出了一種基于改進Fitts 定律的面向VR 放置任務的自然手勢交互時間的預測方法。首先，構建“手勢交互—VR環境—VR交互任務”的交互邏輯；然后，進行自然手勢交互實驗，根據放置任務和改進Fitts 定律確定影響自然手勢交互時間的因素，并建立相應的預測模型，旨在為面向VR 放置任務的用戶交互時間的準確預測提供參考。

1 自然手勢交互和Fitts定律簡介

1.1 自然手勢交互

隨著Leap Motion 控制器、Kinect控制器等體感交互設備的不斷涌現，人機交互逐漸發展為在三維場景中的自然人機交互。為了實現二維場景到三維場景的可視映射，馮志全等［8］利用普通攝像機獲取手勢特征并引入“替身”，提出了一種基于自然手勢交互的三維人機交互方式。張鳳軍等［9］利用智能手機的慣性傳感器控制輸入，實現其與三維場景相連，這種交互方式具有實時、快速和易學習的優點，但難以實現對復雜動作的模擬。為了將手勢交互融入三維體驗系統，吳匯岳等［10］基于“paint-view-correct（描繪—觀察—修正）”構建了手勢界面工具IEToolkit，并將其應用于虛擬家居展示和城市漫游系統，取得了良好的三維交互效果。針對自然手勢與虛擬對象的直接交互，Huang 等［3］開發了一種沉浸式手勢系統，可以在VR環境中利用自然手勢很好地完成與復雜圖形的交互，其交互效果優于利用鼠標、鍵盤的交互。

雖然手勢交互被認為是目前最自然的交互方式之一，但現有的交互效果并不理想，存在人工跟蹤算法使用效率低、長時間交互易引起手部疲勞等不足［11］。因此，筆者在設計放置實驗時，綜合考慮了影響自然手勢交互時間的多種因素，并設計了多種面向VR放置任務的自然手勢。

1.2 Fitts定律

Fitts定律廣泛應用于二維交互界面的設計。針對交互界面的設計，ISO（International Organization for Standardization，國際標準化組織）提出了一種用于預測交互任務難度指數和交互時間的方法［12］。自1954 年Fitts 定律提出以來，其有效性已被諸多研究證明。在人因工程領域，Fitts定律是評價定向裝置有效性的重要數學模型，可用于測定輸入設備的指向和選擇。Fitts定律指出，將物體從一個目標區域移動到另一個目標區域所需的時間是關于目標物寬度和移動距離的函數［13］，其基本公式為：

式中：tM為移動時間；a、b為常數，可通過MATLAB擬合工具箱回歸分析得到［13］；ID為難度指數；A為移動距離；W為目標物寬度。

經典Fitts 定律為完成一維、二維場景中的指向任務提供了較好的理論依據。國內外學者基于經典Fitts定律開展了很多研究，如Dunagan等［14］利用Fitts定律較準確地預測了在觸摸平板上完成指向任務的交互時間。

經典Fitts 定律并不適用于三維場景，因此很多學者對經典Fitts 定律進行了改進。Jeong 等［15］用手指在觸摸屏上滑動來完成三維場景中的指向任務，利用改進的Fitts定律更加精確地預測了完成指向任務的交互時間。Burno 等［16］通過自然手勢完成了三維場景中的指向任務，并與利用鼠標和觸摸屏進行交互作了對比，發現基于自然手勢的交互時間長于基于鼠標和觸摸屏，但自然手勢交互的吞吐率較低。

Deng 等［17］利用光線投射算法對三維虛擬場景中的物體定位任務進行了系統研究，提出了面向VR放置任務的交互時間預測模型，并通過實驗改進了經典Fitts定律。其改進的Fitts定律表示為：

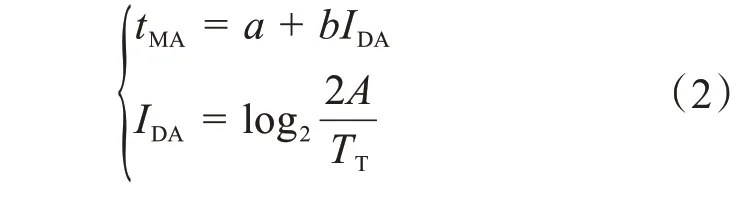
式中：tMA為改進后的移動時間；IDA為改進后的難度指數；TT為目標物容差。

Deng等的研究表明，影響交互時間的主要因素為難度指數、移動距離和目標物容差。通過手柄放置實驗發現，改進Fitts定律還有待進一步優化。Holmes 等［18］利用Leap Motion 控制器將手勢交互應用于VR 環境，所得結果同樣滿足改進Fitts 定律。雖然Deng 和Holmes等均對經典Fitts定律進行了改進，但其并未研究自然手勢交互在VR 放置任務中的適用性以及自然手勢交互時間與實際交互時間之間的一致性問題。基于此，筆者擬基于改進Fitts 定律和自然手勢交互理論，對VR環境中的放置任務作進一步研究，進行面向VR放置任務的自然手勢交互時間的預測。

2 自然手勢交互方法及設計

2.1 “手勢交互—VR 環境—VR 交互任務”交互邏輯

通過對交互方式、交互環境和交互任務的分析，在VR 環境中構建一個合理有效的自然手勢交互框架。在實際生活中，用戶常用的包含交互語義的手勢分為通信型手勢（如手語）和操作型手勢（如操縱具體物體）。在VR環境中，交互對象為虛擬對象和VR界面；交互方式分為桌面交互和自然手勢交互，其中自然手勢交互包括基礎手勢交互和組合手勢交互；交互任務分為導航、對象控制和放置。基于此，根據用戶活動和VR 環境中的交互任務，構建了“手勢交互—VR環境—VR交互任務”交互邏輯，如圖1所示。

圖1 “手勢交互—VR環境—VR交互任務”交互邏輯Fig.1 Interaction logic of"gesture interaction-VR environment-VR interaction task"

2.2 自然手勢設計原則

對于VR環境中的放置任務，Connolly等［19］指出用戶、計算機和任務是VR交互中必不可少的3個重要因素。基于Fitts定律和圖1所示的交互邏輯，提出3條面向VR放置任務的自然手勢設計原則，具體為：

1）用戶體驗原則。以用戶為中心，手勢交互應滿足易學、易操作的要求，符合用戶的正常交互習慣。在設計過程中，應降低無意識操作的影響，提高用戶的操作意識，把握用戶心理和顧及風俗等因素，將簡單手勢復用，減輕用戶學習和記憶的負擔。

2）目標需求原則。在基礎手勢的基礎上設計其他對比手勢，以豐富手勢類型。在本文中，手勢類型的設計須滿足放置任務的要求，確保對應的操作能夠完整地完成放置任務。

3）環境限定原則。設計的手勢應能適應特定環境。考慮到手勢感應范圍的有限性，劃定相應的操作范圍；考慮到手勢遮擋等問題，也須限定操作范圍。

2.3 自然手勢交互設計及語義映射

基于上述自然手勢設計原則，為了準確完成VR放置任務，結合VR 交互特點和用戶行為特點，設計了3種基礎自然手勢，如圖2所示。利用Leap Motion控制器以及虛幻引擎UE4調用手勢指令。在UE4中張手可調用射線，握拳使物體平移，張手和握拳交替進行可以實現物體放置。建立用戶、手勢指令與交互任務之間合理的語義映射關系是人機交互的關鍵。通過自然手勢與交互任務的準確映射，可實現用戶與虛擬對象的準確交互。自然手勢與交互任務之間的語義映射關系如表1所示。其中：自然手勢①適用于二維場景交互，不適用于三維場景交互；自然手勢②、③、④存在手遮擋等問題，在放置較小物體時，移動距離誤差較大；自然手勢⑤、⑥采用控制射線的方式間接完成交互任務，可以移動并放置距離較遠的物體。針對本文研究目的，選用自然手勢⑤、⑥進行面向VR放置任務的自然手勢交互實驗的設計。

圖2 面向VR放置任務的3種基礎自然手勢Fig.2 Three basic natural gestures for VR placement task

表1 自然手勢與交互任務之間的語義映射關系Table 1 Semantic mapping relationship between natural gesture and interaction task

3 面向VR放置任務的自然手勢交互實驗

3.1 實驗目的

VR放置任務如圖3所示。用戶使用自然手勢在VR環境中完成物體放置任務，并對其交互時間進行預測，主要包括：1）在VR 環境中通過自然手勢控制射線移動物體，完成放置任務；2）驗證經典Fitts 定律和改進Fitts 定律預測面向VR 放置任務的自然手勢交互時間的適用性。

圖3 VR放置任務示意Fig.3 Schematic of VR placement task

3.2 實驗設備

面向VR 放置任務的自然手勢交互實驗的設備如圖4 所示。軟件設備：虛幻引擎UE4 和繪圖軟件Vision 等。硬件設備：1 臺搭配LG 曲面屏的Windows10 系統臺式電腦、Leap Motion 控制器和THC頭盔。

圖4 面向VR放置任務的自然手勢交互實驗的設備Fig.4 Equipment of natural gesture interaction experiment for VR placement task

3.3 實驗對象

在貴州大學招募14名學生參與實驗，其中男性9名，女性5名，年齡為（23±2.0）歲，身高為（165.8±9.2）cm。所有參與者均視力正常，為右手使用習慣，且從未使用過Leap Motion 控制器，對VR 設備的操作不熟練。

3.4 實驗方法

在虛幻引擎UE4中搭建一個長、寬均為20 m，高為5 m的VR場景，任務開始前移動球體和目標球體均放在0.5 m×0.5 m×1.0 m立方柱的正中央。參照文獻［17，20］，選取7個不同直徑的移動球體（其直徑SO=0.06，0.12，0.18，0.24，0.30，0.36，0.42 m）、2 個移動距離（A=0.6，1.6 m）和3 個不同的目標物容差（TT=0.1，0.2，0.3 m）。在VR環境中，移動球體為綠色球體；目標球體為半透明的黃色球體，其直徑W=0.16～0.72 m。為了確保移動球體出現在用戶視覺范圍內，移動球體和目標球體距離地面的高度均為0.8 m，移動球體與實驗對象的距離為1 m。考慮到用戶移動物體的習慣，設物體移動方向為水平方向。根據設計的實驗任務，每名參與者須完成42個放置任務，每個放置任務重復10 次，則每名參與者須完成420次實驗，共采集14×420=5 880個實驗數據。

在VR空間中，移動物體的速度v與其在水平方向（x方向）上的分量vx的大小基本一致，而另外2 個方向的分量vy和vz較小，對移動物體速度的影響較小，因此采用水平方向作為物體的移動方向來設計手勢交互實驗。

3.5 實驗過程

在實驗前，提醒實驗者注意實驗事項，并協助他們佩戴好HTC頭盔，調整好所在位置。隨后，讓實驗者完成如下任務：迅速、準確地用自然手勢將移動球體放入目標球體，如圖5所示。

面向VR 放置任務的自然手勢交互實驗的場景如圖6所示。實驗者使用自然手勢⑤和⑥執行放置任務，即張手發射射線，然后迅速握拳，快速、準確地選中移動球體并將其放置到目標球體中。在實驗過程中，實驗者張手將射線朝向移動球體，當射線觸及移動球體時，其表面出現藍色光標且顏色由綠變紅；當實驗者將移動球體完全放入黃色目標球體時，移動球體立即變成綠色，并發出清脆的“叮鈴”聲，提示放置任務成功，記錄此時的交互時間。成功完成一次放置任務后，實驗者停頓6 s再進入下一個試次。每名實驗者的實驗時間為40 min 左右。在正式開始前，實驗者可進行20 次適應性練習，時長大約為5 min，練習結束后進行正式實驗。

3.6 實驗結果及分析

在實驗過程中，由于實驗者長時間保持操作狀態導致手部疲勞以及Leap Motion 控制器自身的靈敏度問題，使得一部分實驗數據無效，因此須剔除無效數據再進行數據的處理和分析。有2名實驗者將移動球體放入目標球體的失誤率為50%和43%，因此他們的實驗數據為無效數據，予以剔除。其余12名實驗者的失誤率為（7.381±2.143）%，其實驗數據予以保留，則共獲得5 040個有效數據。當實驗者出現個別組10次放置任務均未完成的情況時，采用該組對應條件下的總體平均值代替。對12名實驗者的自然手勢交互時間取平均值，得到每個組別的交互時間tMA。實驗結果如表2所示。

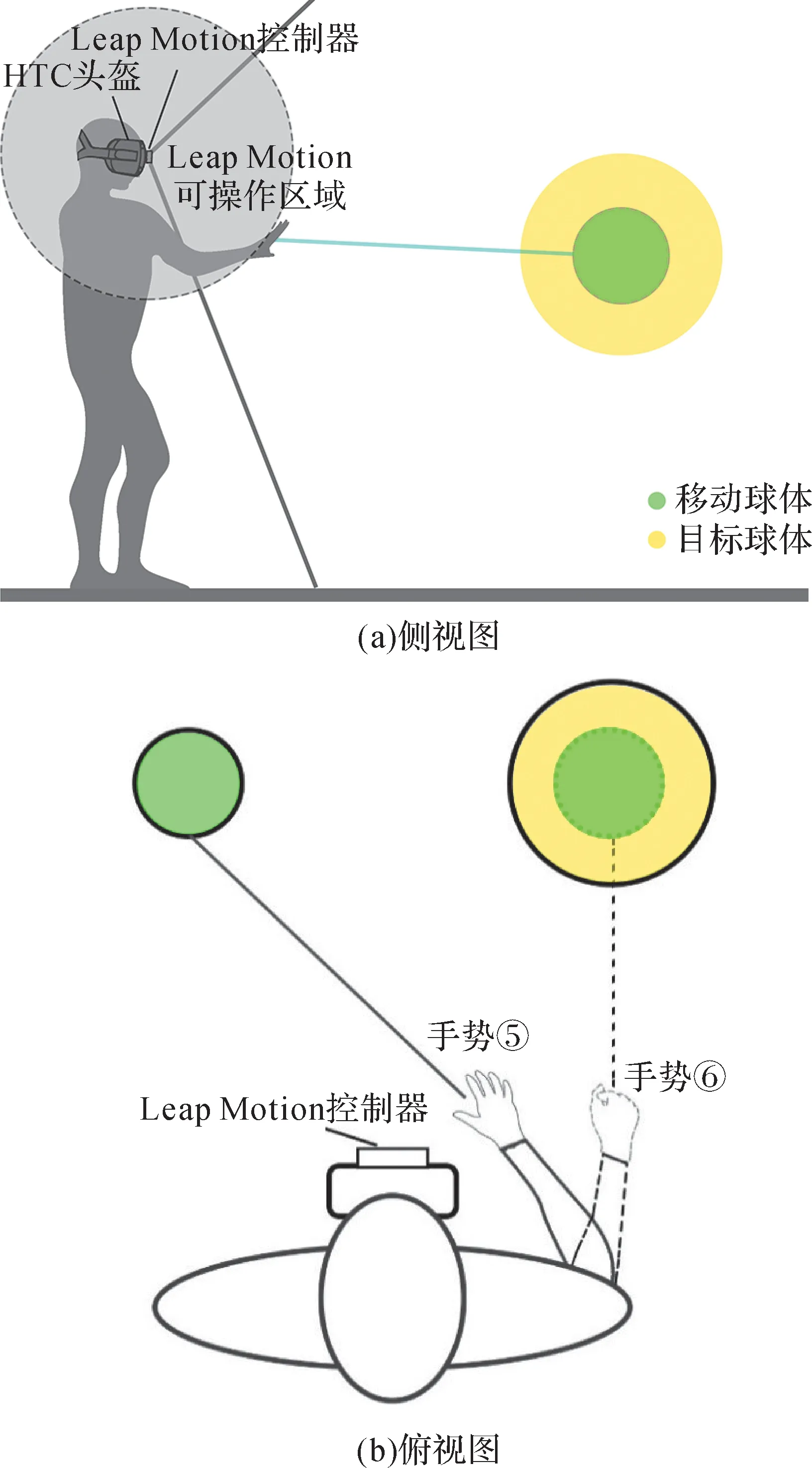
圖5 面向VR放置任務的自然手勢Fig.5 Natural gestures for VR placement task

圖6 面向VR放置任務的自然手勢交互實驗的場景Fig.6 Scene of natural gesture interaction experiment for VR placement task

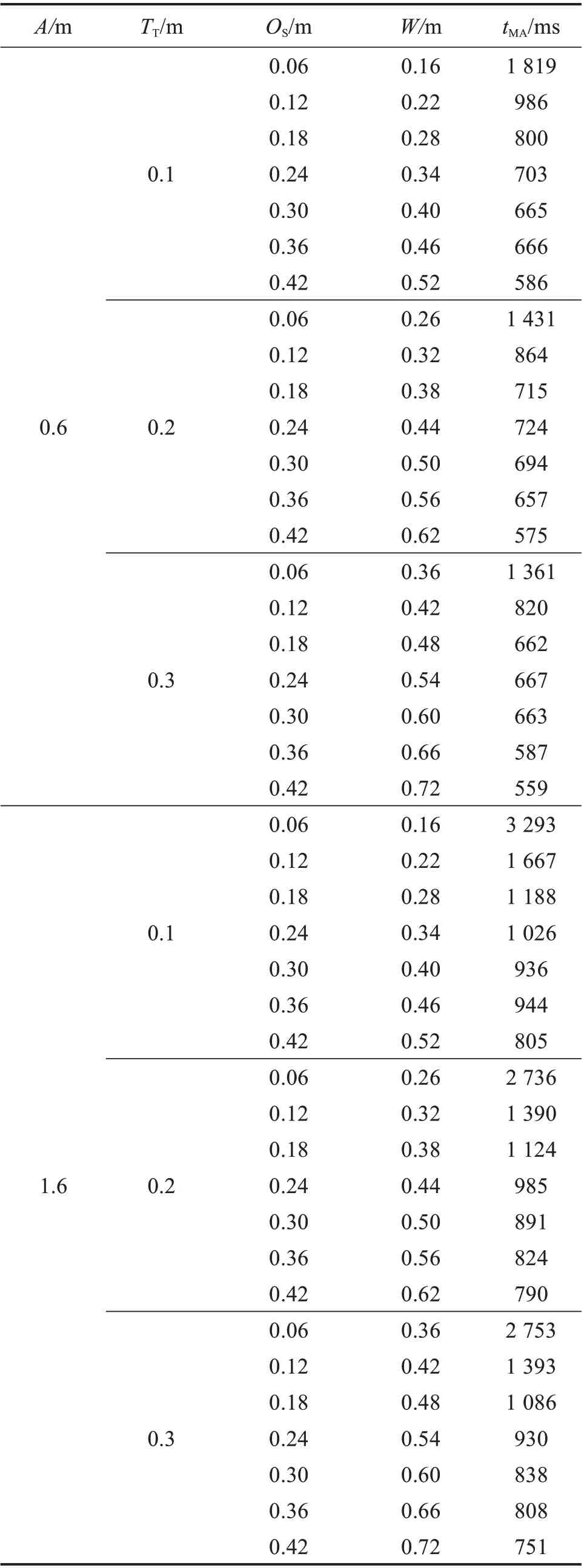
表2 面向VR放置任務的自然手勢交互實驗的結果Table 2 Results of natural gesture interaction experiment for VR placement task

根據表2，制作了面向VR 放置任務的自然手勢交互時間與各影響因素的關系，如圖7所示。為了分析移動距離、目標物容差和移動球體直徑對自然手勢交互時間的影響，在SPSS（statistical product and service solutions，統計產品與服務解決方案）軟件中，進行2×3×7 的三因素重復測量方差分析，設水平點α=5%。通過箱式圖判斷，各組數據無異常值。經過Mauchly 球形度檢驗后可知，移動距離、目標物容差和移動球體直徑的p＜0.05，違背了Mauchly球形度檢驗，須進行Greenhouse-Geisser矯正。通過主體內效應檢驗可得，對于移動距離，F（1，11）=110.264，p＜0.001，p=0.000（經Greenhouse-Geisser矯正），說明其對交互時間有顯著效應，交互時間隨移動距離的增大而顯著增長，如圖7（a）所示；對于目標物容差，F（1.160，12.757）=108.633，p＜0.001，p=0.000（經Greenhouse-Geisser矯正），說明其對交互時間的主效應也較為顯著，交互時間隨目標物容差的增大而快速縮短，如圖7（b）所示；對于移動球體直徑，F（3.026，33.283）=27.192，p＜0.001，p=0.000（經Greenhouse-Geisser 矯正），說明其對交互時間的主效應也較為顯著，交互時間隨著移動球體直徑的增大而縮短，但是當球體直徑增大到0.24 m后，交互時間的變化逐漸趨于平緩，如圖7（c）所示。由于目標球體直徑隨目標物容差和移動球體直徑的變化而變化，為了得到其對交互時間的影響，作交互時間隨目標球體直徑的變化曲線，如圖7（d）所示。隨著目標球體直徑的增大，交互時間并不一直減小，說明移動球體直徑和目標物容差存在交互作用。為了判斷交互項因變量（移動距離、目標物容差和移動球體直徑）的交互作用是否具有統計學意義，進行了Mauchly 球形度檢驗，檢驗發現交互項因變量的p＜0.05，須進行Greenhouse-Geisser 矯正；F（3.793，41.721）=45.146，p＜0.001，p=0.000（經Greenhouse-Geisser 矯正），說明移動距離、目標物容差和移動球體直徑的交互作用對交互時間的主效應顯著，具有統計學意義。另外，移動球體直徑對交互時間的影響與真實環境中的結果存在差異。VR 放置任務不同于二維平面上的指向任務，移動物體大小對交互時間有顯著影響，因此在預測交互時間時不可忽略該因素。

4 面向VR放置任務的自然手勢交互時間的測定

圖7 面向VR放置任務的自然手勢交互時間與各影響因素的關系Fig.7 Relationship between the natural gesture interaction time and the influencing factor for VR placement task

將實驗數據導入MATLAB擬合工具箱［13］，采用多元線性回歸分析法進行回歸分析。基于經典Fitts定律擬合得到的相關系數R2=0.515，結果如圖8（a）所示。通過回歸分析得出：a=-23.241，其95%CI（confidence interval，置信區間）為［-383.26，336.78］；b=480.28，其95%CI為［331.49，629.06］。將a、b代入式（1），可得：

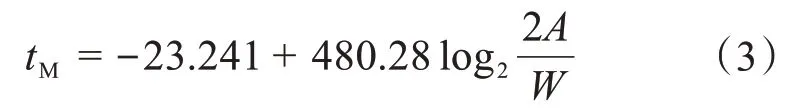
圖8（a）表明交互時間預測值與真實值間存在偏差。出現偏差的原因有2個：1）未考慮移動球體的直徑；2）未考慮目標物容差。通過上文分析可知，移動物體大小和目標物容差對交互時間有顯著性影響，在構建面向VR 放置任務的自然手勢交互時間預測模型時須考慮這2個因素。式（1）展開后變為：

Deng等利用目標物容差TT代替目標物寬度W，基于式（2）擬合得到的相關系數R2=0.927，表明采用目標物容差TT更合理。基于上文三因素重復測量方差分析結果可知，交互時間與移動物體大小成反比。考慮移動物體大小的影響，對式（2）進行改進，可得［17］：

圖8 面向VR 放置任務的自然手勢交互時間與難度指數的關系Fig.8 Relationship between the natural gesture interaction time and the difficulty index for VR placement tasks

利用MATLAB擬合工具箱，基于式（5）擬合得到的相關系數R2=0.970，結果如圖（b）所示。其中：a=51.56，其95% CI 為［-79.95，183.1］；b=135.40，其95% CI 為［100.6，170.1］；c=0.611，其95% CI 為［0.446，0.777］。對比圖8（a）和圖8（b）可知，基于式（5）的擬合結果優于基于經典Fitts定律的擬合結果。將a、b、c代入式（5），可得：

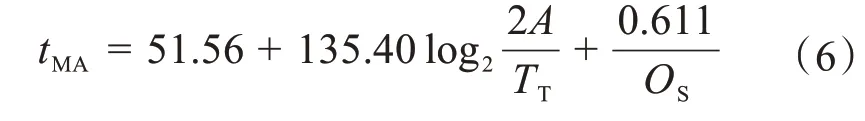
由上文分析可知，在自然手勢交互中，移動距離、目標物容差和移動物體大小對交互時間的影響程度不同，且移動距離和目標物容差對交互時間的影響更大，而式（2）只體現了移動距離和目標物容差的影響，式（6）則體現了移動距離、目標物容差和移動物體大小對交互時間的影響。進一步分析圖8（b）發現，有些點不在擬合曲線上甚至嚴重偏離。通過方差分析可知，除了因控制器抖動造成的人為誤差外，偏離點對應的均是直徑較小的移動球體，因此必須考慮移動物體大小對交互時間的影響。故在自然手勢交互時間的預測上，式（6）的預測精度更高。

根據表2 數據和公式（6）進行計算，得到自然手勢交互時間隨難度指數的變化曲線，如圖9所示。對比圖9（a）和圖9（b）發現：移動距離越大，目標物容差越小，則難度指數越大，對應的交互時間越長；移動球體直徑越小，其對應的交互時間越長。

圖9 基于改進Fitts 定律的自然手勢交互時間隨難度指數的變化曲線Fig.9 Changing curve of natural gestur interaction time with difficulty index based on improved Fitts Law

5 結 論

自然手勢交互是一種重要的VR界面交互方法。利用自然手勢進行了VR放置任務的研究，通過實驗對面向VR 放置任務的交互時間進行了測定。基于改進Fitts定律的自然手勢交互時間的預測為后續物體VR的放置和使用研究提供了基礎，為VR 環境中人機交互界面的設計提供指導。