基于滾筒載荷的采煤機滑靴振動分析及實驗驗證
白楊溪,陳洪月,,陳洪巖,王 鑫,李建剛,
(1.遼寧工程技術大學機械工程學院,遼寧 阜新 123000;2.遼寧工程技術大學礦產資源開發利用技術及裝備研究院,遼寧 阜新 123000)
采煤機作為煤礦井下綜采工作面的主要設備,其運行狀態直接影響開采效率。由于井下煤層結構復雜,采煤機在截割過程中會產生劇烈振動。振動不僅會對采煤機的截割性能及生產效率產生影響,還會通過機身傳遞至行走部——滑靴,加速滑靴的磨損,從而縮短采煤機的使用壽命[1-4]。因此,對采煤機的振動特性進行分析是十分重要的。目前,國內外許多學者已針對采煤機的振動特性展開相關研究。例如:劉春生等考慮煤層傾角和俯仰角等因素,構建了采煤機整機力學模型,并采用Krylov 子空間方法和最小二乘法進行求解,獲得了煤層傾角和俯仰角對采煤機滑靴力學特性的影響規律[5-6];毛君等考慮煤巖硬度和牽引速度等因素,構建了采煤機豎直方向和水平方向的動力學模型,并利用數值仿真方法進行求解,分析了煤巖硬度和牽引速度對采煤機關鍵部件振動的影響[7-8];陳洪月等對隨機激勵和多種混合激勵下采煤機機身及搖臂的振動特性進行了研究[9-11];姜鵬等以MG400/930-WD 型滾筒采煤機為研究對象,構建了采煤機垂直方向的動力學模型,并采用MATLAB軟件進行求解,分析了搖臂擺角、滾筒轉速和外載荷等因素對采煤機動力學特性的影響[12];武健康等通過構建采煤機整機的動力學理論模型,并利用ADAMS(automatic dynamic analysis of mechanical systems,機械系統動力學自動分析)軟件進行虛擬仿真,驗證了理論模型的準確性[13];Liu等搭建了采煤機行走部振動測試試驗臺,并基于測試數據分析了采煤機行走部的振動規律[14];Zhang等對采煤機的振動特性進行了時域分析和頻域分析,獲得了采煤機機身不同部位的振動規律[15]。
目前,學者們對采煤機的研究主要集中在采煤機整機靜力學特性以及單一方向上采煤機整機動力學特性等方面,而對采煤機整機耦合動力學特性的研究較少。為此,筆者采用拉格朗日法構建采煤機整機動力學模型,并選用Wilson-θ算法對動力學模型進行求解,得到采煤機滑靴的三向振動加速度曲線,最后通過采煤機振動實驗來驗證理論模型的準確性。
1 采煤機整機動力學模型構建
由于采煤機整機的結構復雜,在構建采煤機整機動力學模型時,須對采煤機進行簡化處理。以采煤機的機械結構為主導,忽略電氣系統、液壓系統以及輔助系統,根據采煤機的結構特征及其各部件的功能,將采煤機劃分成前、后滾筒,前、后搖臂,機身,前、后導向滑靴以及前、后平滑靴等9個部分。構建采煤機三向耦合動力學模型,如圖1 所示。圖中:Rfx、Rfy、Rfz分別為前滾筒在側向方向(X方向)、垂直方向(Y方向)、牽引方向(Z方向)上所受的載荷;Rbx、Rby、Rbz分別為后滾筒在側向方向、垂直方向、牽引方向上所受的載荷;lo、wo、ho分別為機身的長度、寬度、高度;la為搖臂的長度;mfd、mbd分別為前、后滾筒的質量;mfa、mba分別為前、后搖臂的質量;mo為機身的質量;mfg、mbg為分別前、后導向滑靴的質量;mfs、mbs分別為前、后平滑靴的質量;φfa、φba分別為前、后搖臂的舉升角;ψfa、ψba分別為前、后搖臂的擺角;θfox、θbox為前、后搖臂繞機身X方向的轉角;θfoy、θboy分別為前、后搖臂繞機身Y方向的轉角;kij為連接剛度,其中i表示連接的部件,i∈{ofg,obg,ofs,obs,ofa,oba,fgp,bgp,fsc,bsc},分別表示機身與前導向滑靴、機身與后導向滑靴、機身與前平滑靴、機身與后平滑靴、機身與前搖臂、機身與后搖臂、前導向滑靴與銷排、后導向滑靴與銷排、前平滑靴與鏟煤板和后平滑靴與鏟煤板的連接,j表示方向,j∈{X,Y,Z};cij為阻尼,i、j含義與上同;ffg、fbg分別為前導向滑靴的摩擦力;ffs、fbs分別為平滑靴的摩擦力;xb、yb、zb分別為部件b(b∈{o,fg,bg,fs,bs})的X、Y、Z向振動位移。
根據圖1,采用拉格朗日法構建采煤機三向耦合動力學方程。
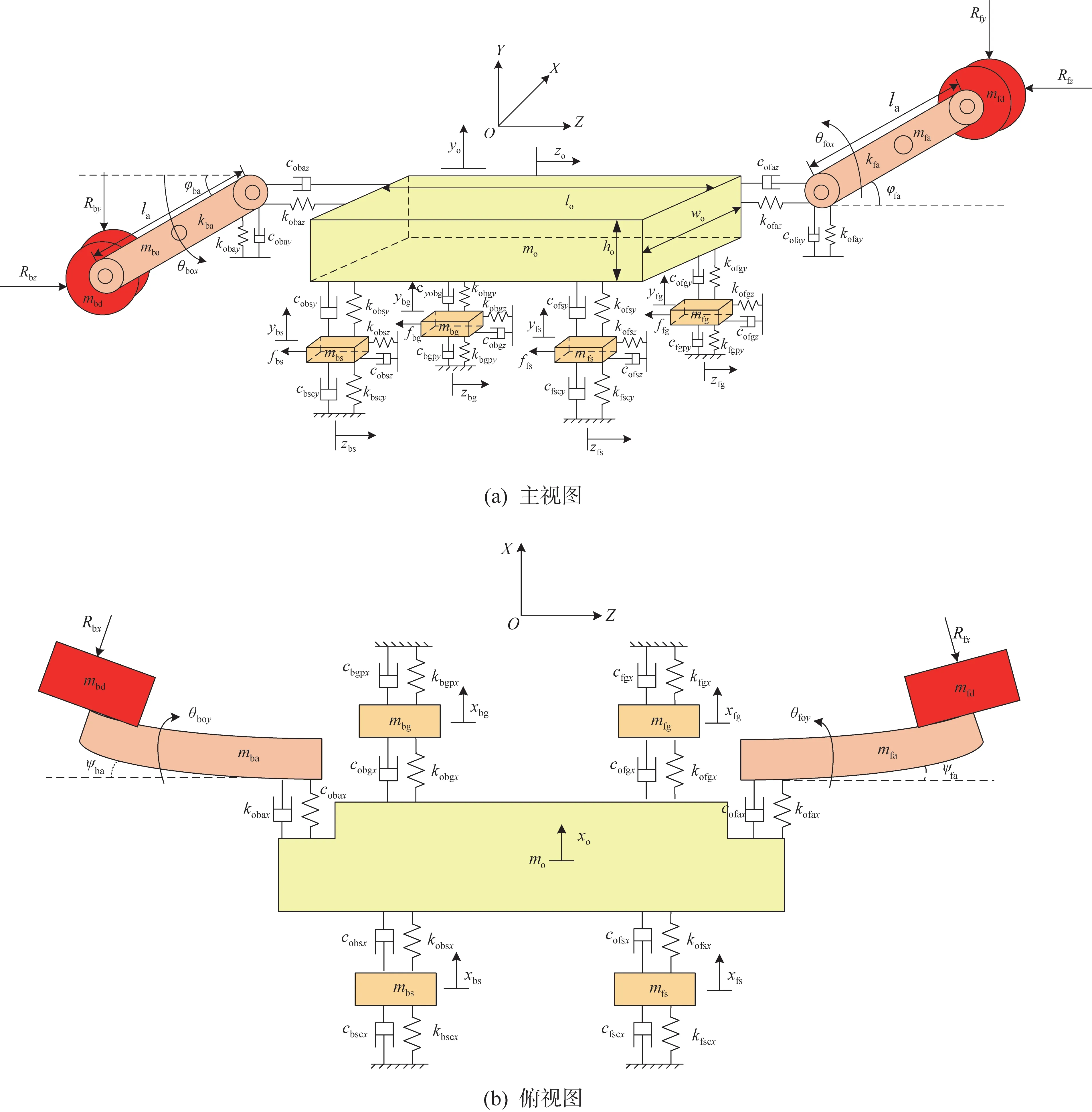
圖1 采煤機三向耦合動力學模型Fig.1 Three-directional coupling dynamics model of shearer
采煤機振動系統的動能T為:

其中:
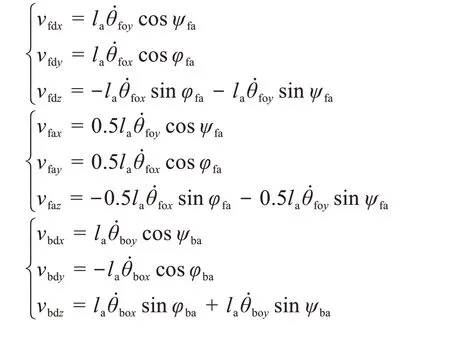

采煤機振動系統的勢能U為:



采煤機振動系統的耗散能D為:
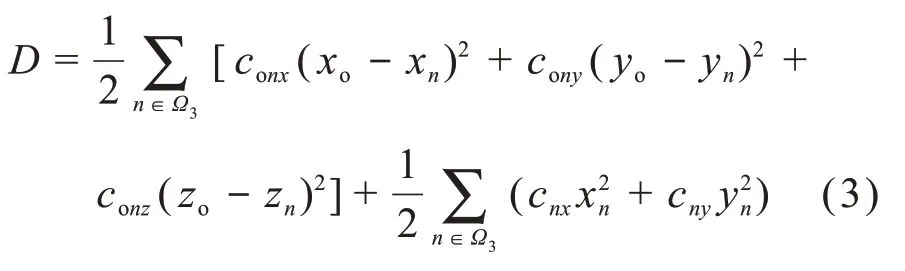
拉格朗日方程可表示為:
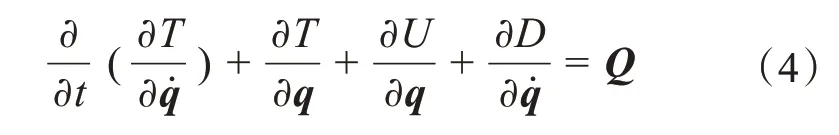
式中:q為廣義坐標;Q為外界激勵。

將式(1)至式(3)代入拉格朗日方程,整理可得:
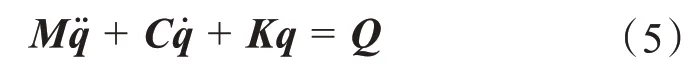
其中:
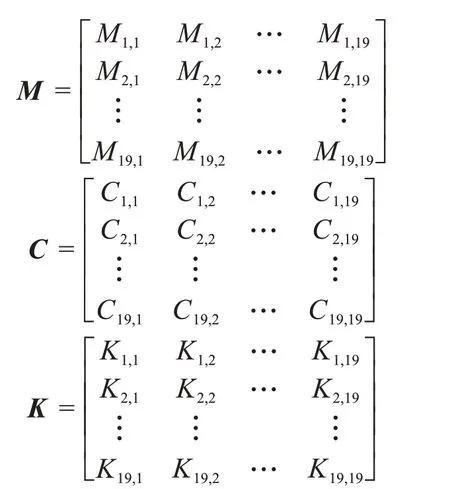
式中:M、C、K分別為質量、阻尼和剛度矩陣。
質量矩陣M為對稱矩陣,其主對角線上的元素為:
人才隊伍的建設是工程質量的人員保障,同時也不應當放棄對先進管理經驗的學習。先進的質量管理經驗不僅能夠提升工作效率,還能提升質量管理的效果。公路工程建設施工的管理非常復雜,其管理主體呈現多元化的趨勢,如果不能進行科學有效的管理,就可能導致整個公路工程建設停滯不前。可見科學合理的管理工作能夠適應各種環境下的工程施工。對于整個工程質量能夠進行有效管理。企業也應該定期舉辦專業講座,邀請行業內頂尖的工程質量管理人員對員工進行有效培訓,讓員工緊跟新的管理理念的步伐,增強自身對于先進管理經驗的敏感程度,時刻保持對先進管理理念的熱情。

其他非零元素為:
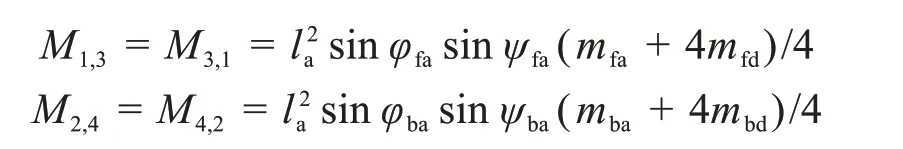
阻尼矩陣和剛度矩陣同樣為對稱矩陣,此處不再詳細列舉。質量矩陣、阻尼矩陣和剛度矩陣均為非對角矩陣,即矩陣中存在耦合項[16-17]。對于多自由度無阻尼振動系統,可采用模態坐標法對其動力學模型進行解耦。將質量矩陣M和剛度矩陣K代入頻率方程Δ(ω2)=|k-ω2m|=0,求得系統的自然頻率ω,然后將ω代入(K-ω2M)Φ=0,可得到系統的模態向量矩陣。令q=Φx,通過坐標變換,可得:
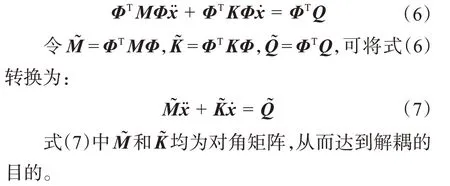
對于多自由度有阻尼振動系統,其頻率方程為Δ(ω2)=|k-ω2m+jωc|=0。假設系統的自由度為N,當阻尼矩陣對稱正定時,其頻率方程的解為N對共軛復數。對于具有N個自由度的有阻尼振動系統,其存在2N個復模態,而獨立變量僅為N個,故無法采用模態坐標變換法對其動力學模型進行解耦,而數值求解方法可有效解決這類耦合問題。因此,本文采用Wilson-θ算法對式(5)進行求解,計算步驟如下。
步驟1 給出初始值x0、、,設置總時長為T。
步驟2 設置時間步長Δt及θ,計算積分常數:
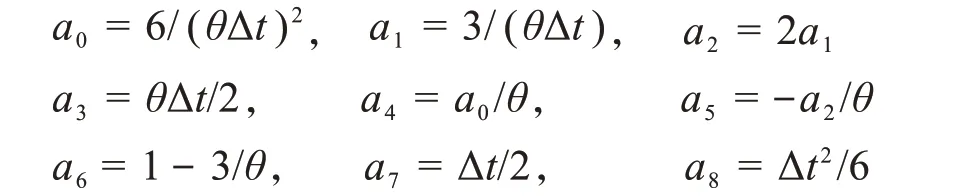
步驟3 計算t+θΔt時刻的有效載荷Qt+θΔt:
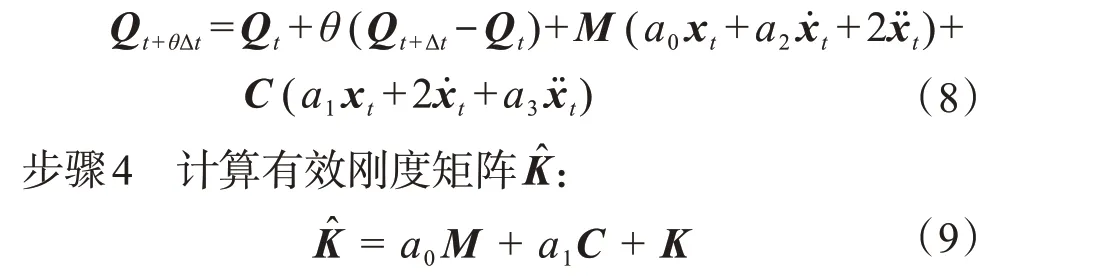
步驟5 計算t+θΔt時刻的位移xt+θΔt:

步驟7 重復步驟3至步驟6,直至t+Δt≥T。
2 采煤機滑靴振動測試實驗
為了驗證所構建的采煤機三向耦合動力學理論模型的準確性,借助國家能源煤礦采掘機械裝備研發(實驗)中心的1∶1模擬煤礦井下真實環境的采煤機實驗平臺進行采煤機振動測試。以采煤機滑靴(如圖2(a)、(b)所示)為主要研究對象,在其開槽處安裝三向無線振動加速度傳感器,通過無線網關接收傳感器信號并傳輸至上位機。采煤機滑靴處的振動加速度傳感器布置情況如圖2(c)所示。
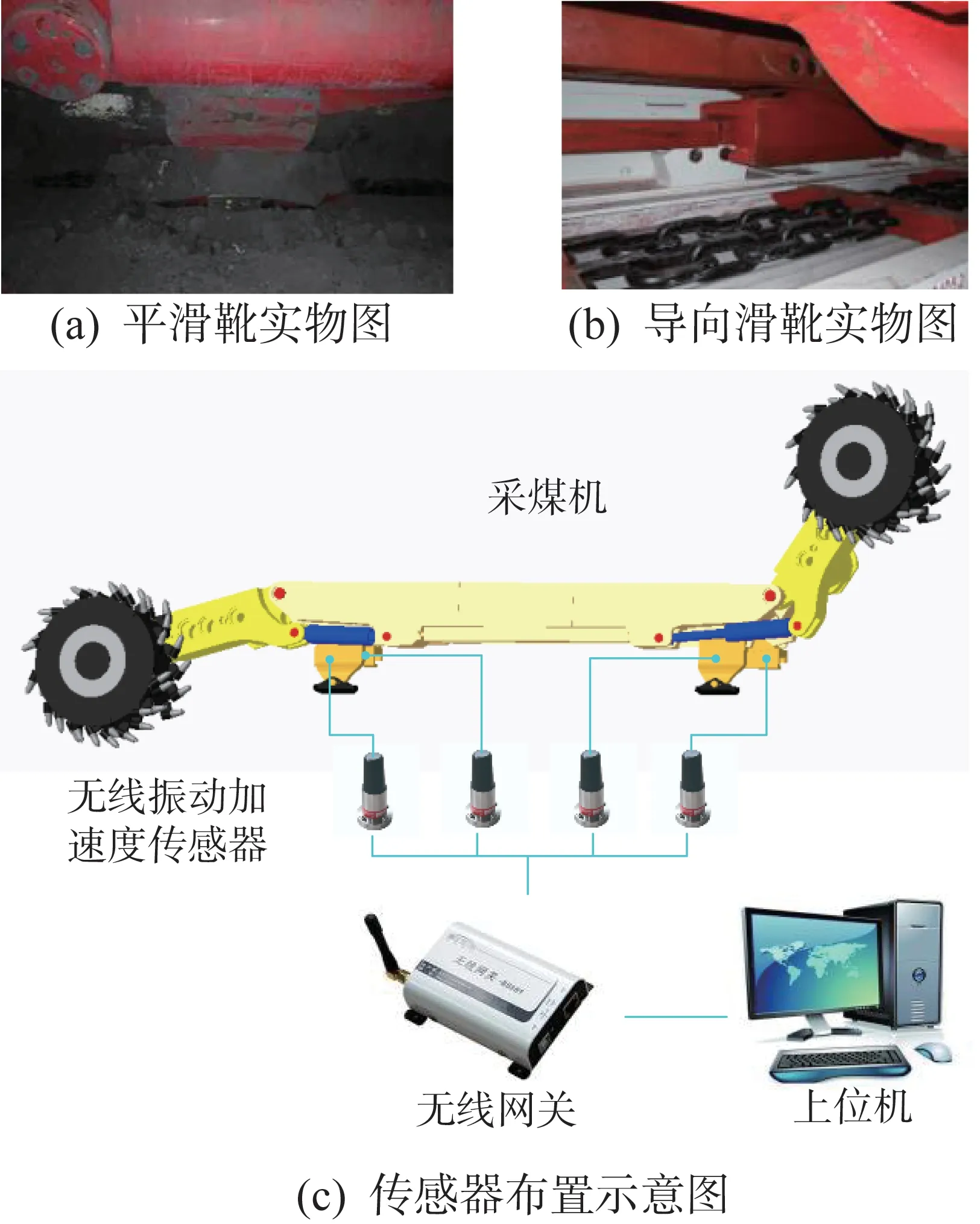
圖2 采煤機滑靴處振動加速度傳感器的布置情況Fig.2 Arrangement of vibration acceleration sensor at the sliding shoe of shearer
為采集采煤機截齒所受的載荷,在采煤機截齒上安裝DH1210型應變傳感器(如圖3(a)、(b)所示),用于采集其截齒所受的三向載荷。采煤機截齒上應變傳感器的布置情況如圖3(c)所示。
采煤機截齒所受載荷的采集及傳輸過程與滑靴振動信號類似,安裝在截齒上的應變傳感器將力學信號轉變為電信號,經無線應變采集模塊和無線通信主站接收模塊的傳輸,最終傳遞至上位機。
采煤機滑靴振動實驗現場如圖4所示,實驗條件為:煤壁高度為3 m,煤壁硬度為3;采煤機型號為MG500/1130WD,其滾筒轉速為32 r/min,牽引速度為3 m/min,工作面總長度為70 m;實驗總時長為22 min,采樣頻率為20 Hz。根據文獻[18]中的公式,將DH1210 型應變傳感器采集的截齒所受載荷轉換為前、后滾筒所受載荷,其時間歷程曲線如圖5所示。
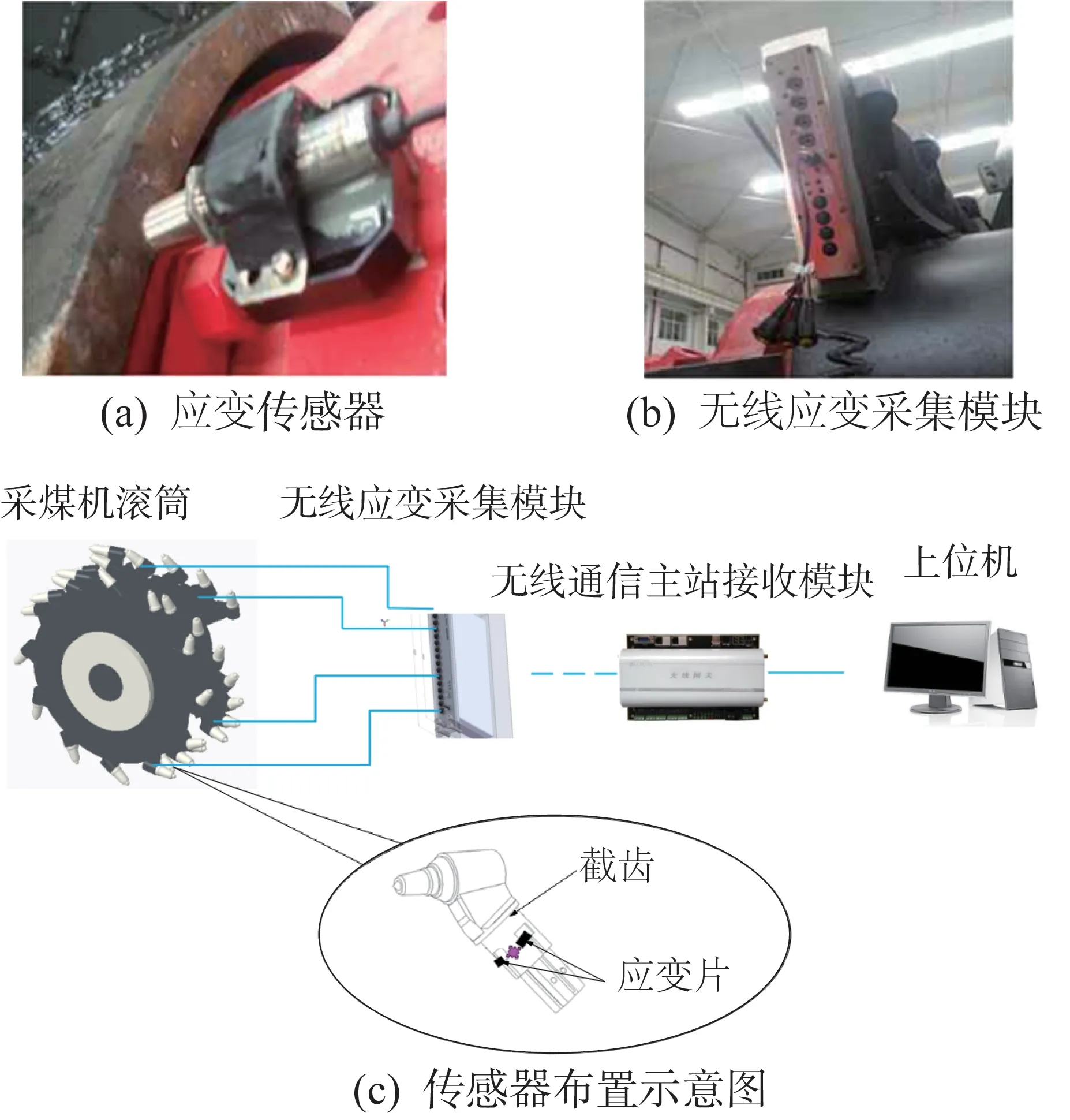
圖3 采煤機截齒上應變傳感器的布置情況Fig.3 Arrangement of strain sensors on picks of shearer

圖4 采煤機滑靴振動實驗現場Fig.4 Vibration experiment site of shearer sliding shoe
3 采煤機滑靴動力學仿真及結果對比
基于上述分析,選用MG500/1130WD型采煤機為研究對象,對其動力學特性進行仿真分析。該型采煤機的結構參數如表1所示。設采煤機前搖臂的舉升角φfa=30°,后搖臂的舉升角φba=-15°,采用Wilson-θ算法對式(5)進行仿真求解,設置仿真時長為10 s,將通過實驗測得的采煤機滾筒所受載荷作為激勵輸入。通過仿真分析,得到采煤機導向滑靴、平滑靴的三向振動加速度仿真曲線,并與實驗曲線進行對比,結果如圖6和圖7所示。
由圖6和圖7可知,采煤機導向滑靴和平滑靴的Y向最大振動加速度約為5 m/s2,大于其他2 個方向的振動加速度,而X向最大振動加速度與其他2個方向的振動加速度相差1個數量級,說明采煤機滑靴的側向振動很小,相對其他2個方向的振動來說可被忽略。采煤機導向滑靴與平滑靴在3個方向上對應的最大振動加速度相近。
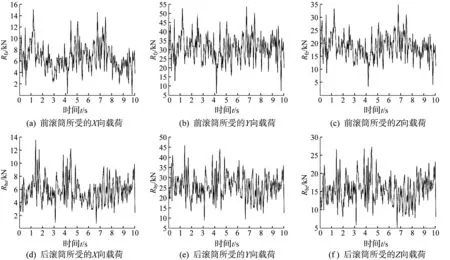
圖5 采煤機滾筒所受載荷的時間歷程曲線Fig.5 Time-history curve of load on shearer drum

表1 MG500/1130WD型采煤機的結構參數Table 1 Structural parameters of MG500/1130WD shearer
雖然采煤機滑靴最大振動加速度的仿真值與實驗值相差不大,但須對其中位數、相關系數和P值等指標進行對比,以更準確地分析振動加速度的分布規律以及仿真結果與實驗結果的相似程度。其中,相關系數選用皮爾遜(Pearson)相關系數。
采煤機滑靴振動加速度仿真值與實驗值對比的箱線圖以及其相關系數和P值直方圖如圖8所示。
由圖8(a)可知,采煤機滑靴振動加速度仿真值與實驗值的中位數均集中在平衡位置“0 m/s2”上,從整體上看,仿真結果的四分位數全距大于實驗結果,表明仿真結果相對發散、而實驗結果更為聚集;仿真結果和實驗結果的異常值均較少,說明采煤機滑靴的振動加速度不具有偏態性。由圖8(b)可知,采煤機前、后導向滑靴,前、后平滑靴的三向振動加速度的仿真值與實驗值的相關系數分別為0.582,0.668,0.481,0.596,0.544,0.654,0.311,0.381,0.377,0.492,0.432和0.583,各相關系數均大于0.3,呈實相關,部分相關系數大于0.5,呈顯著相關。由圖8(c)可知,采煤機前、后導向滑靴,前、后平滑靴的三向振動加速度的仿真值與實驗值的P值均大于0.05,說明在95%置信區間內,仿真結果與實驗結果無顯著差異。
4 結 論
為了研究采煤機滑靴的振動特性,將采煤機劃分成前、后滾筒,前、后搖臂,機身,前、后導向滑靴以及前、后平滑靴等9個部分。采用拉格朗日法構建采煤機三向耦合動力學模型,并對動力學模型的坐標耦合問題進行分析,選用Wilson-θ算法對所構建的動力學模型進行求解,得到采煤機滑靴的三向振動加速度仿真曲線。通過分析仿真曲線,得到采煤機滑靴的垂直方向振動加速度最大,側向方向振動加速度相對較小。最后,通過采煤機振動實驗測得采煤機滑靴的三向振動加速度,并與仿真結果進行對比。通過比較采煤機滑靴三向振動加速度仿真值與實驗值的中位數、相關系數以及P值等指標發現,仿真結果與實驗結果有較好的一致性,說明仿真結果可以近似替代實驗結果,同時也驗證了采煤機三向耦合動力學理論模型的準確性。

圖6 采煤機導向滑靴振動加速度時間歷程曲線對比Fig.6 Comparison of vibration acceleration time-history curves of shearer guide sliding shoe
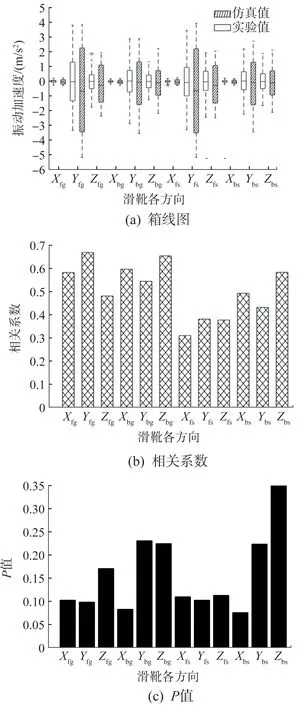
圖8 采煤機滑靴振動加速度仿真結果與實驗結果對比的評價指標Fig.8 Evaluation index for comparison of simulated result and experimental result of shearer sliding shoe vibration acceleration

