使民以時

王小靜

摘要：孔子曰：“道千乘之國，敬事而信，節用而愛人，使民以時。”孔子是站在君主治理天下的立場，從物質時間的節約角度提出要求。“十年樹木百年樹人”有些事情或許可以得過且過，但教學不能敷衍塞責，來不得半點馬虎。作為教師，我們應站在育人、教學的立場，從時間成本的角度去要求自己提高教學質量，打造“陽光高效課堂”。

關鍵詞：陽光高效課堂；學案；自主探索；變式與發散

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2021）09-0071

在“減負提質”的教育理念下，我校提出了“陽光高效課堂”，為我們九年級復習課堂指明了方向，在九年級復習課中如何取得高效？這些問題困惑著筆者，一節課的時間極為有限，在有限的時間里將整章知識點逐一講到，是不現實也是不科學的。“使民以時”給筆者很大的啟發，真正領悟“陽光高效課堂”中的高效，把握時間、教學以時，提高教學效率。

一、教學相長

只有思考的教師才能引導學生思考，而思考著的學生反之亦能促使教師思考，如果教師沒有這個意識，那么“取法乎下”，學生只能“僅得下下”，談何效果。所以，教師要做到“學生未思我先想”“我與學生共成長”。在教學中，筆者搭建知識體系，串聯學科網絡通過“聯”性問題的出示，使學生在短時間內有效地建構數學知識網絡，在整理復習中進而掌握了知識的應用。例如，我們在復習矩形性質這節課時要掌握并運用矩形的以下知識：矩形的四個角都是直角；對角線互相平分且相等；對角線把矩形分成兩對全等的直角三角形；矩形是軸對稱圖形；矩形的面積等于兩鄰邊的乘積。

問題出示：如圖，矩形ABCD的兩條對角線相交于點O，

（1）找找圖形中有哪些特殊的三角形。

（2）要添加什么條件時，能使△AOB更特殊呢？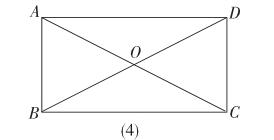

（3）在（2）的基礎上，能不能求出對角線的長度？若不能，那要增加什么條件呢？若AB=4cm，矩形ABCD的對角線是多少？

（4）過點D作DE∥AC，交BC的延長線于E，這時，∠DBE與∠DEB有什么特殊的關系？

“聯”在問題上，有時我們也“聯”在圖形上，筆者在課堂上也是經常設計。時常總結鞏固，學會觸類旁通。“學而時習之”學習了時時練習，時常進行整理和復習，獲得知識和智慧。我們在講述一個問題后，若能及時總結和鞏固練習，才會達到觸類旁通的效果，進行思維。

二、多算勝少算不勝

多算勝，少算不勝，古代一種作戰思想。語源于《孫子·計篇》：“夫未戰而廟算勝者，得算多也，未戰而廟算不勝者，得算少也。多算勝，少算不勝，而況于無算乎！吾以此觀之，勝負見矣。”意為作戰前計算周密，勝利條件多，可能勝敵；計算不周，勝利條件少，就不能勝敵。深化變式練習，筆者有時要一題多講和變式練習，來引導學生尋找解決問題策略的多樣化及優化，促使學生的思維得到發散和升華。在一題多講中，學生可以從不同的角度分析、解決問題，促使學生根據自己的認知基礎和思維特點進行選擇，發現具有個性差異的解題方法，從而使每一個學生探索出解決問題的有效方法。展現不同解法，發散學生的思維，發展學生的數學思維能力。變式練習是為了把問題講透、思路展開揭示本質，促使學生的分析能力得到提高、認識得到深化。試題變式促進學生對知識點本質的掌握，在對知識進行系統梳理，形成知識網絡的同時對典型問題進行變式訓練，達到舉一反三、觸類旁通的目的。

三、好為人師授人以漁

孟子說：“人之患在于好為人師。”總以為自己知道的，不遺余力地去教給學生，生怕學生自己弄不明白。可是教不是萬能的。陶行知先生告訴我們：教是為了不教。教學生知識，不如讓學生學會怎么學，所謂“授人以魚，不如授人以漁”。九年級的學生有獨立思考和探索知識的能力，并能通過閱讀課本，結合自己的理解逐漸完善自己的想法，把所學內容整理成有綱有目的內容體系，抓住思想方法的脈絡，把書本看“薄”，從而發現知識之間的聯系，學會知識之間的轉化，做到心中有數、觸類旁通，促進知識技能的形成。此外，教師還要善用網絡，事半功倍。利用釘釘上的學習功能上傳一些資料和視頻供學生學習，讓學生及時完成，并及時反饋學生的做題情況。這樣，在備課時可以更有針對性，對上課的教學內容更有指向性，從而收獲更好的效果。

四、三省吾身

僅僅停留在做題與改錯題的層面上，那么所謂使得內化、能力的培養與智慧的提升便成為一句空話。針對不同層次的學生，教師可以引導學生做好復習反思。在復習中有一種簡單而又高效的方法，那就是編寫錯集。讓我們把有限的、寶貴的時間全都花在自己最該花時間的地方，以保證自己有限的精力真正做到“好鋼用在刀刃上”，同時也避免了復習時的單調與乏味。編寫的目的是誘導學生暴露他們原有的思維方法和過程，利用它來反思自己學習中存在的問題，尋找錯誤產生的原因。通過反思，可以加深對知識的掌握、提高數學的思維能力，調動其學習的積極性，培養學生的思維能力，保證每一個字、每一個步驟都不能出錯，不能再犯類似的錯誤，給學生對待學習、對待成長以深刻的啟迪。另外，教師提供一些資料、開放性的問題來引導學生圍繞一定的主題，根據自身能力選一些“跳一跳可以摘得到”的題目自行練習，讓學生感悟數學思想方法，體會探究實際上并不神秘，也并非高不可攀。同時，教師還要進行自主探索，使學生在探索的過程中進一步理解所學知識，讓學生經歷多角度認識問題、多種形式表現問題、多種策略思考問題、嘗試解釋不同解答的合理性，以發展其創新意識和實踐能力。在完成的過程中，學生運用所學知識提出問題、解決問題，對學生的解題能力和方法也有了質的飛躍。

筆者不敢奢望在教育事業的大課堂中能“得其志”“得其人”，僅“得其曲”“得其數”的筆者明白論語中的“雖曰未學，吾必謂之學矣”，也就是說真正的學習者、研究者首先是行動者。在已“得其志”的教師的指引下，路是正確的，教育的前方是光明的，我們只有行動起來，以勤補拙，才會有所進步、有所領悟，爭取做到“使民以時”為學生打造“陽光高效課堂”。

參考文獻：

[1]胡愛民.用《論語》思想提升數學教育智慧[M].重慶：西南師范大學出版社，2010.

（作者單位：浙江省溫州市第二十中學325011）