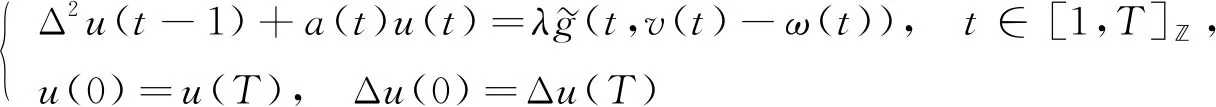一類含參半正二階離散周期邊值問題正解的存在性

王 瑞, 路艷瓊

(西北師范大學 數學與統計學院, 蘭州 730070)

0 引 言

微分方程或差分方程邊值問題在計算機科學、 物理學、 經濟學、 生態學、 動力系統、 機械系統及交通系統等領域應用廣泛. 目前, 邊值問題正解的研究已由非線性項正定的條件逐漸拓展到非線性項具有負下界的情形, 這類問題稱為半正問題. Castro等[1]在考察二階微分方程Dirichlet邊值問題

(1)

非負解的存在性時, 提出了半正假設:f(0)<0.Anuradha等[2]用錐上不動點定理考察了二階微分方程

(2)

正解的存在性, 其中λ>0為參數,f: [r,R]×[0,∞)→連續, 且存在常數M>0, 使得f(t,u)≥-M,t∈[r,R],u≥0.Webb等[3]在半正情形下建立了任意階微分方程

u(n)(t)=λf(t,u(t)),λ>0

(3)

多個正解的存在性.Zhu等[4]基于Leray-Schauder非線性抉擇和Guo-Krasnoselskii不動點定理研究了含參半正二階微分方程周期邊值問題

(4)

正周期解的存在性和多解性, 其中λ>0是參數,f: [0,2π]×[0,∞)→滿足Carathédory條件. 金立蕓等[5]用Guo-Krasnoselskii不動點定理討論了二階差分方程m-點特征值問題

(5)

至少一個正解的存在性, 其中f: [0,∞)→連續, 且存在常數M>0使得f(y)≥-M,t∈[a+1,b],λ>0為參數,α,β,ν,δ∈[0,∞),ci,di∈[0,∞),i∈{1,2,…,m-2}.李建平等[6]利用錐拉伸與錐壓縮不動點定理在非線性項具有負下界和非減性條件下, 討論了二階半正定非線性差分方程

(6)

正解的存在性, 其中T>1是一個給定的正整數.

離散周期邊值問題是一類重要的差分問題, 在非線性項f非負的情形下關于其解的存在性與多解性研究已有很多結果[7-10].王晶晶等[8]在非線性項f非負時給出了

(7)

正解的存在性結果, 其中a: [1,N]→(0,∞), 且但目前關于半正離散周期邊值問題正解的存在性研究尚未見文獻報道, 基于此, 本文研究半正二階離散變系數周期邊值問題

(8)

其中λ>0, [1,T]={1,2,…,T},a: [1,T]→(0,∞)且連續, 且滿足如下假設:

(H1) 存在常數D>0, 使得f(t,u)≥-D, (t,u)∈[1,T]×[0,∞);

(H3) 存在兩個常數b,d∈(0,∞), 使得0

1 預備知識

令[a,b]={a,a+1,…,b}, 設u(t)是定義在[a,b]上的函數, 則Δu(t)=u(t+1)-u(t)稱為u(t)在t點的一階差分, Δ稱為(前向)差分算子, 記I為恒等算子, 即Iu(t)=u(t).當n2

E∶={u|u: [0,T+1]→,u(0)=u(T), Δu(0)=Δu(T)},

由文獻[11]中推論2.5可知, 問題(8)對應的齊次問題

(9)

是非共軛問題, 只有平凡解且格林函數G(t,s)>0, (t,s)∈[1,T]×[1,T].

設φ和ψ分別是初值問題

的唯一解, 則:

1)φ(t)≥0且Δφ(t)≥0,t∈[1,T];

2)ψ(t)≥0且Δψ(t)≤0,t∈[1,T].

引理1[11]設a: [1,T]→(0,∞)且則問題(9)的格林函數為

(10)

引理2設u滿足邊值問題

(11)

其中v: [1,T]→且v≥0, 則

證明: 設存在t0∈[1,T], 使得‖u‖=u(t0), 則對?t∈[1,T], 有

(12)

證明: 對?t∈[1,T],

1) ‖Au‖≤‖u‖, ?u∈K∩?Ω1; ‖Au‖≥‖u‖, ?u∈K∩?Ω2;

2) ‖Au‖≥‖u‖, ?u∈K∩?Ω1; ‖Au‖≤‖u‖, ?u∈K∩?Ω2.

2 主要結果

(13)

(14)

(15)

的解, 則

由引理2可知, 對?u∈K,

即AK?K, 且因為E是有限維空間, 故易證A:K→K是全連續的.

定義Ω1={u∈E|‖u‖<1}.設u∈K∩?Ω1, 則

即?u∈K∩?Ω1, ‖Au‖≤‖u‖.

從而

故

且

于是

即?u∈K∩?Ω2, ‖Au‖≥‖u‖.

則問題(8)至少存在兩個正解, 其中C2=max{|f(t,u)||t∈[1,T], 0≤u≤L}.

證明: 由定理1的證明可知, 問題(8)存在第一個正解u1滿足‖u1‖>m/(2M).下面證明存在第二個正解.記

(16)

則0

考慮問題(8)的輔助問題:

(17)

定義Ω3={u∈E|‖u‖

即?u∈K∩?Ω3, ‖Fu‖≤‖u‖.

定義Ω4={u∈E|‖u‖

其中t*∈[1,T]為任意一點.因此?u∈K∩?Ω4, ‖Fu‖≥‖u‖.

注2文獻[8]建立了非線性項f≥0且格林函數G(t,s)≥0時問題(7)正解的存在性結果, 本文在G(t,s)>0時將非線性項f推廣到半正情形, 得到了問題(8)正解的存在性與多解性結果.

例1考慮二階離散周期邊值問題：

(18)

容易驗證對?t∈[1,10]和u∈[0,∞), 有即存在一個常數使得假設(H1)成立;對?t∈[1,10]一致成立, 即假設(H2)成立; 存在正常數使得即假設(H3)成立.因此由定理1可知, 當時, 問題(18)至少存在一個正解; 由定理2可知, 當

時, 問題(18)至少存在兩個正解.