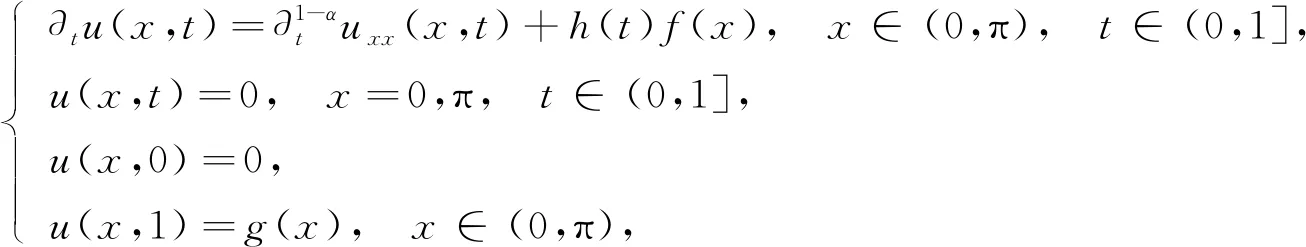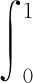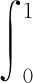帶有Riemann-Liouville導數的分數階熱傳導方程逆源問題的正則化方法
史暖峰, 馮立新
(1. 黑龍江大學 數學科學學院, 哈爾濱 150080;2. 利沃夫國立理工大學 應用數學與基礎科學學院, 烏克蘭 利沃夫 79013)
0 引 言
熱傳導方程逆源問題是一類重要的熱傳導反問題, 目前已得到廣泛關注. 文獻[1]把熱能量作為測量數據重構僅依賴于時間的逆源問題, 數值上采用邊界元法與二階Tikhonov正則化法, 通過廣義Fourier方法證明了反問題解的存在性、 唯一性以及對測量數據的連續依賴性; 文獻[2]把若干空間上的積分作為測量數據重構二維熱傳導方程的熱源項, 數值上采用共軛梯度法對該問題進行求解; 文獻[3]根據初始數據和邊界數據及兩個附加數據重構熱傳導方程中的兩個可分離源項, 并提出了一種連續逼近的數值迭代算法; 文獻[4]把僅依賴于時間的逆源問題轉化為第一類Volterra積分方程, 用Tikhonov正則化方法求解了該問題; 文獻[5]基于分離變量法, 利用Tikhonov正則化方法, 重建時間分數階熱傳導方程熱源項, 并分析了正則解的收斂性; 文獻[6]研究了帶有Caputo導數的一階時間分數階熱傳導方程反問題, 并基于特征函數展開, 利用解析延拓反演源項證明了時間分數階只與空間變量有關的源項反問題的唯一性; 文獻[7]基于疊加原理, 提出了一種改進的擬邊界值方法解決時間分數擴散方程的逆源問題; 文獻[8]利用Landerweb迭代正則化方法解決時間分數階擴散方程逆源問題, 并給出了先驗和后驗兩種選取策略下正則解和精確解的誤差估計; 文獻[9]采用分數階Landerweb方法反演了未知空間源項, 該方法優于傳統Landerweb方法, 計算速度較快; 文獻[10]研究了多項時間分數階擴散方程, 根據Laplace變換證明了解的衰減率由時間分數導數的最小階數給出; 文獻[11]研究了帶有Riemann-Liouville導數的熱擴散方程反問題, 利用準邊界值法克服問題的不適定性, 給出了先驗參數選取時正則解和精確解的誤差估計. 目前, 對帶有Caputo導數的分數階熱傳導逆源問題已有許多研究成果, 但對于帶有Riemann-Liouville導數的分數階熱傳導方程逆源問題的研究文獻報道較少. 本文主要討論帶有Riemann-Liouville導數的分數階熱傳導方程逆源問題, 利用分離變量和Laplace變換構造Tikhonov正則化近似解, 并證明正則解的收斂性.
1 問題描述
考慮如下分數階導數熱傳導方程:

(1)
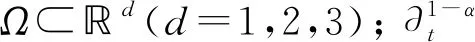

(2)
Γ(·)是Gamma函數;A是一個對稱的橢圓算子[13], 定義為

(3)
逆源問題: 給定A,h(t), 根據末時刻T的觀測數據gδ(x)重構未知源項f(x), 其中觀測數據gδ(x)滿足
‖gδ(x)-g(x)‖L2(Ω)≤δ,
(4)
這里δ為誤差水平.
2 正則解的構造及誤差估計
橢圓算子A在Ω上滿足齊次Dirichlet邊值條件的特征值與規范的特征向量(λp,φp(x)), 即

(5)
利用分離變量法假設精確解u(x,t)為
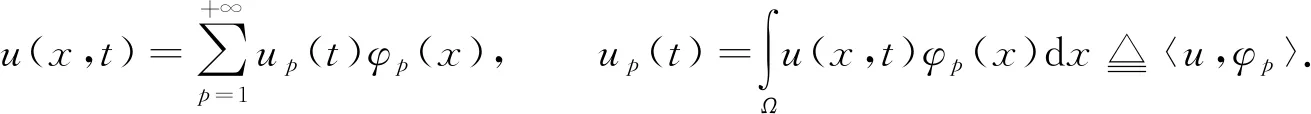
(6)
對方程(1)中t變量做Laplace變換, 有
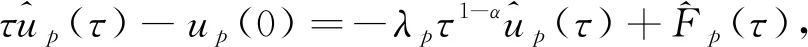
(7)
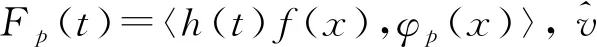
根據文獻[12]可知,
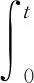
(8)
其中Eα,β是Mittage-Leffler函數[14], 其定義為

利用u(x,0)=0和Fp(τ)=〈h(τ)f(x),φp(x)〉, 可得
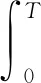
(9)
從而可得
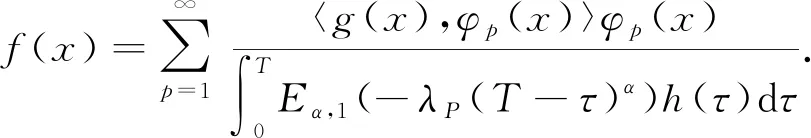
(10)

下面引進線性算子K:L2(Ω)→L2(Ω), 定義為
其中

(12)
引理1[11]K是L2(Ω)→L2(Ω)上的自伴緊算子且為單射.
本文考慮的逆源問題可抽象地寫為如下算子方程形式:
Kf(x)=g(x).
(13)

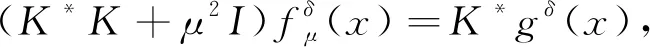
(14)
其中μ>0, 為正則化參數.由式(12),(14)計算得
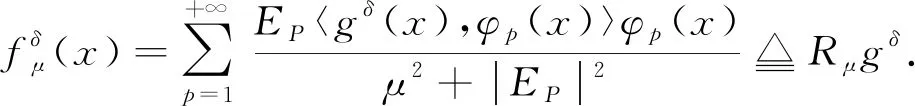
(15)
2.1 先驗參數選取下正則解與精確解的誤差估計
假設fμ(x)是如下方程的解:
K*Kfμ(x)+μ2fμ(x)=K*g(x).
(16)
由算子K的定義易知

(17)
由式(15),(17)得
即

(18)
引理2設f(x)∈Hk(Ω),E為常數, 滿足E≥‖f‖Hk(Ω), 則如下估計成立:

(19)
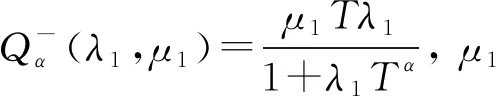
證明: 由式(10),(17)可得


(20)
根據文獻[11]知,

(21)
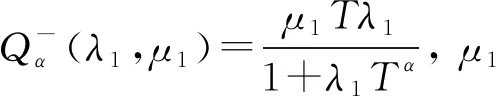

(22)
情形1) 當0 N1={p∈,, (23) 則有 選取m=1-k且‖f(x)‖Hk(Ω)≤E, 有 即 (24) (25) 從而式(19)成立, 證畢. 根據引理2, 式(26)有兩種情形. 情形1) 當0 情形2) 當k≥1時, 有 (28) 由引理2和式(27),(28)可得如下定理. 基于Morozov相容性原理, 選取正則化參數, 即選擇μ>0, 使得 (29) 直接計算可得 某公司6萬t/a鎳電解項目采用硫化鎳電解精煉工藝,主要包括電解、三段凈化、電溶造液3個子項,于2012年8月建成投產。在項目論證、設計、建設過程中,充分考慮了混酸體系含有介質腐蝕環境,結合防腐新技術的發展,對本項目防腐方法進行了優化改進。6萬t/a鎳電解項目整體工程質量優良,并獲得了2012至2013年度中國建筑行業工程質量最高榮譽——魯班獎。項目建成后經過5年多的生產運行跟蹤,生產能力達到或超過設計指標,防腐效果基本達到了生產運行要求,保障了生產的順利、穩定運行。 (30) 因此 即 從而 于是 (31) 證明: 因為 假設觀測數據gδ(x)滿足條件(4)和‖gδ(x)‖≥τδ, 則有 由式(14)知 再結合式(29)得 (32) 根據式(31),(32)可知選取后驗參數時, 正則化參數選取范圍為 (33) 由式(29),(33)可得如下定理. 定理2在后驗參數選取準則(29)下, 正則化參數的選取范圍為式(33). 所以 于是 (34) 因為K:L2(Ω)→L2(Ω)是有界線性算子, 對任意z∈L2(Ω), 有 (35) 所以 即 (36) 又因為K:L2(Ω)→L2(Ω)是單射算子, 所以Range(K*)在L2(Ω)中稠密, 由式(36)可知 由式(29),(36)可得如下定理. 為驗證本文正則化方法的可行性, 下面給出求解分數階導數逆源問題的實例.考慮邊值問題: (37) 其中 方程(37)的精確解為 u(x,t)=t1+αsin(3x). 數值實驗過程如下: 1) 對空間Ω進行等距剖分, 剖分節點為 2) 對g(x)加擾動可得觀測數據gδ(x): eprand(·)=δ(2rand(·)-1),gδ(·)=g(·)(1+eprand(·)); 3) 為方便比較, 給出精確解和正則解的相對誤差為 4) 根據文獻[15]的算法計算Mittag-Leffler函數, 利用 可得 由式(15)得正則解為 表1列出了5種α取值下精確解和先驗參數選取正則解的相對誤差, 表2列出了5種α取值下精確解和后驗參數選取正則解的相對誤差, 其中α∈{0.1,0.3,0.5,0.7,0.9}.圖1為先驗參數選取時精確解和正則解的比較, 圖2為后驗參數選取時精確解和正則解的比較, 其中N=50,α∈{0.1,0.3,0.5,0.7,0.9}. 表1 先驗參數選取精確解與正則解的相對誤差 表2 后驗參數選取精確解與正則解的相對誤差 由表1、 表2及圖1、 圖2中反演結果可見, 當δ→0時, 誤差減小, 正則解接近于精確解, 且后驗參數選取策略結果優于先驗參數選取策略, 表明本文的正則化方法有效. 圖1 先驗參數選取精確解與正則解的比較Fig.1 Comparison between exact solution and regularization solution for priori parameter choice rule 圖2 后驗參數選取精確解與正則解的比較Fig.2 Comparison between exact solution and regularization solution for posterior parameter choice rule 綜上, 本文利用Tikhonov正則化方法, 討論了帶有Riemann-Liouville導數的分數階熱傳導方程逆源問題, 給出了先驗正則化參數選取時正則解的收斂速度估計及后驗正則化參數選取時正則化參數的取值范圍, 并證明了其正則解的弱收斂性. 數值實驗結果表明該方法有效.


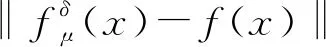







2.2 后驗參數選取下正則解與精確解的誤差估計

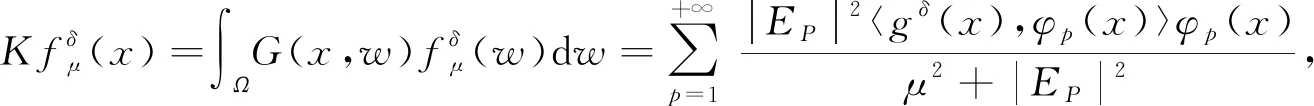
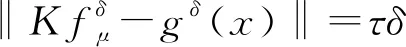
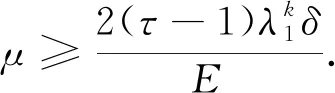

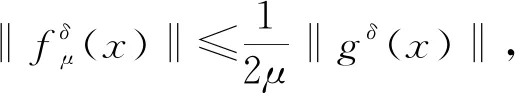



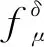



3 數值實驗