低維Hom-Jacobi-Jordan代數的分類

李 小 朝

(黃淮學院 數學與統計學院, 河南 駐馬店 463000)

1 引言與預備知識

Hom-代數是一類更廣泛的代數結構, 目前已得到廣泛關注： 文獻[1-2]將李代數的Jacobi等式通過線性映射進行形變得到了Hom-李代數, Hom-李代數可視為通常李代數的一種形變或推廣； Hu[3]給出了李代數形變的q-李代數； 文獻[4-6]研究了Hom-李代數的結構和低維分類等； 文獻[7-8]分別在低維Leibniz代數分類和低維Poisson代數分類的基礎上, 利用待定系數法給出了低維Hom-Leibniz代數分類和低維Hom-Poisson代數分類. 文獻[9]通過將向量空間L上李代數的反對稱性條件[x,y]=-[y,x]換為對稱性條件[x,y]=[y,x](?x,y∈L), 給出了Jacobi-Jordan代數的概念, 指出Jacobi-Jordan代數是一類特殊的Jordan代數, 并給出了其低維分類； 文獻[10]將Jordan代數的研究推廣到δ-Jordan李超代數上, 研究了帶有對稱根系的任意分裂δ-Jordan李超代數的結構； 文獻[11]給出了二次Hom-Leibniz代數的概念， 并研究了其若干重要性質; 文獻[12]考慮滿足Jacobi等式的交換代數——Mock李代數, 即Jacobi-Jordan代數. Jacobi-Jordan代數可通過反結合代數, 即滿足(xy)z+x(yz)=0的代數, 類似于結合代數構造李代數的方法實現. 類似于文獻[1-2,4]構造Hom-李代數的方法, 本文將Jacobi-Jordan代數的Jacobi等式通過線性映射進行扭曲, 給出Hom-Jacobi-Jordan代數, 并利用待定系數法, 給出低維Hom-Jacobi-Jordan代數的分類.

定義1[9]設L是數域K上的向量空間, 二元運算[,]:L×L→L是雙線性的, 滿足[x,y]=[y,x]和Jacobi等式： ?x,y,z∈L, [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0.則稱(L,[,])是一個Jacobi-Jordan代數.

定義2設(L,[,],α)是一個三元組, 其中L是數域K上的向量空間,α:L→L是一個線性映射, 二元運算[,]:L×L→L是雙線性的, 若對?x,y,z∈L, 滿足下列條件:

1) [x,y]=[y,x];

2) [α(x),[y,z]]+[α(y),[z,x]]+[α(z),[x,y]]=0.

則稱(L,[,],α)是一個Hom-Jacobi-Jordan代數. 條件2)稱為Hom-Jacobi等式.若還滿足α是自同態：α([x,y])=[α(x),α(y)], 則稱(L,[,],α)為保積Hom-Jacobi-Jordan代數.

注1當α是恒等變換時, Hom-Jacobi-Jordan代數即為Jacobi-Jordan代數.

定義3設(L,[,],α)為Hom-Jacobi-Jordan代數.若L的子空間L1滿足α(L1)?L1,[L1,L1]?L1, 則稱(L1,[,],α|L1)是(L,[,],α)的Hom-子代數.若L的子空間L2滿足α(L2)?L2, [L2,L]?L2, 則稱(L2,[,],α|L2)是(L,[,],α)的Hom-理想.

定義4設(L1,[,]1,α1)和(L2,[,]2,α2)是兩個Hom-Jacobi-Jordan代數,f:L1→L2是一個線性映射.若對?x,y∈L1, 均有f([x,y]1)=[f(x),f(y)]2和f°α1=α2°f, 則稱f是一個Hom-Jacobi-Jordan代數同態.特別地, 若f是可逆的線性映射, 則稱f是一個Hom-Jacobi-Jordan代數同構, 且(L1,[,]1,α1),(L2,[,]2,α2)是同構的.

注2若Hom-Jacobi-Jordan代數(L1,[,]1,α1)和(L2,[,]2,α2)同構, 則線性映射α1和α2相似.

命題1設(L,[,])是一個Jacobi-Jordan代數,α:L→L是L的自同態.?x,y∈L, 令[x,y]α=α([x,y]), 則(L,[,]α,α)是一個保積Hom-Jacobi-Jordan代數.

證明： 由于α([x,y])=[α(x),α(y)], 因此

[α(x),[y,z]α]α=α([α(x),α([y,z])])=α2([x,[y,z]]),

結論易證.

命題2設(L,[,],α)是一個保積Hom-Jacobi-Jordan代數,α是可逆的.?x,y∈L, 令[x,y]α-1=α-1([x,y]), 則(L,[,]α-1)是一個Jacobi-Jordan代數.

證明： 由于α([x,y])=[α(x),α(y)]和α可逆, 故有α-1([x,y])=[α-1(x),α-1(y)], 從而可得

因此(L,[,]α-1)是一個Jacobi-Jordan代數.

注3保積Hom-Jacobi-Jordan代數(L,[,],α)(α可逆)均可由Jacobi-Jordan代數及其自同構利用命題1的方法得到.

定義5設(L1,[,],α1),(L2,[,],α2)是Hom-Jacobi-Jordan代數(L,[,],α)的理想, 且L有線性子空間的直和分解L=L1+L2, 則稱(L,[,],α)為理想(L1,[,],α1)和(L2,[,],α2)的直和, 記為(L,[,],α)=(L1,[,],α1)⊕(L2,[,],α2).

2 主要結果

文獻[9]在同構意義下給出了低維Jacobi-Jordan代數的分類. 因此, 本文給出的低維Hom-Jacobi-Jordan代數分類, 都不是Jacobi-Jordan代數. 用span(x1,x2,…,xk)表示向量空間L中元素x1,x2,…,xk生成的子空間.

引理1[9]設(L,[,])為Jacobi-Jordan代數, 則在同構意義下, 有:

1) 二維Jacobi-Jordan代數有J20: [xi,xj]=0(i,j=1,2)和J21: [x1,x1]=x2；

2) 三維Jacobi-Jordan代數有J30: [xi,xj]=0(i,j=1,2,3),J31: [x1,x1]=x2和J32: [x1,x1]=x2, [x3,x3]=x2(本文未給出的括積均為0, 下同).

定理1設(L,[,],α)為保積Hom-Jacobi-Jordan代數, 若α=0, 則：

證明： 由于α=0, 則有α(x)=0(?x∈L), 即Hom-Jacobi等式成立.因此只需L中某些元素不滿足Jacobi等式.證畢.

下面給出的保積Hom-Jacobi-Jordan代數(L,[,],α)都是α非零的情形.

證明： 設[x1,x1]=ax1,α(x1)=bx1, 由Hom-Jacobi等式可得3a2bx1=0.由于α非零, 因此有b≠0, 從而可得a=0, 即[x1,x1]=0, 證畢.

定理3設(L,[,],α)為二維保積Hom-Jacobi-Jordan代數,x1,x2是L的一組基, 則在同構意義下, 有:

證明： 設

[x1,x1]=a11x1+a12x2, [x1,x2]=a21x1+a22x2, [x2,x2]=a31x1+a32x2,

再設α在基x1,x2下的矩陣為B=(bij)2×2.由定義4知, 只需考慮矩陣B對應的Jordan標準形即可.

定理4設(L,[,],α)為三維保積Hom-Jacobi-Jordan代數,x1,x2,x3是L的一組基,α的秩為3, 則Hom-Jacobi-Jordan代數(L,[,],α)也是Jacobi-Jordan代數.

證明： 由于α的秩為3, 則α是可逆的.由命題1和命題2知, 只需對Jacobi-Jordan代數求出自同構, 利用命題1的方法即可構造Hom-Jacobi-Jordan代數.

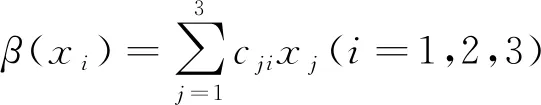
對J32: [x1,x1]=x2, [x3,x3]=x2同理可證.證畢.

定理5設(L,[,],α)為三維保積Hom-Jacobi-Jordan代數,x1,x2,x3是L的一組基,α的秩為2, 則在同構意義下, 有:

1) 對B1,B2, 由于α是自同態, 即α([xi,xj])=[α(xi),α(xj)](i,j=1,2,3), 可得

a13=a23=a33=a41=a42=a51=a52=a61=a62=0.

由x2,x2,x3滿足Hom-Jacobi等式, 可得a53=0.再由x1,x1,x3滿足Hom-Jacobi等式, 可得a43=0.即有

[x1,x1]=a11x1+a12x2, [x1,x2]=a21x1+a22x2, [x2,x2]=a31x1+a32x2,

[x1,x3]=[x2,x3]=0, [x3,x3]=a66x3.

令x1,x2和x3生成的子空間分別為L1=span(x1,x2)和L2=span(x3),α1=α|L1,α2=α|L2=0, 則(L1,[,],α1)和(L2,[,],α2)均為(L,[,],α)的理想, 即有(L,[,],α)=(L1,[,],α1)⊕(L2,[,],α2).

因此有(L,[,],α)?(J20,[,]β1,β1)⊕(L2,[,],α2)或(L,[,],α)?(J21,[,]β2,β2)⊕(L2,[,],α2), 當a66≠0時, (L,[,],α)不是Jacobi-Jordan代數.

3) 對B4同理可得.證畢.

定理6設(L,[,],α)為三維保積Hom-Jacobi-Jordan代數,x1,x2,x3是L的一組基,α的秩為1, 則在同構意義下, 有:

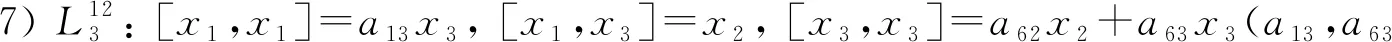
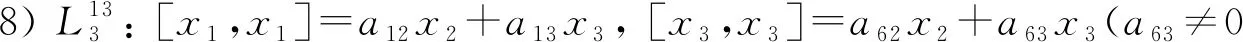
1) 對B5, 由于α是自同態, 即α([xi,xj])=[α(xi),α(xj)](i,j=1,2,3), 可得a12=a13=a21=a31=a41=a51=a61=0.由x1,x1,x1滿足Hom-Jacobi等式, 可得a11=0.再由x1,x1,x2滿足Hom-Jacobi等式, 可得

a22a22+a42a23=0,a23a22+a43a23=0.

(1)

同理由xi,xj,xk(i,j,k=1,2,3)滿足Hom-Jacobi等式, 分別可得

a22x+a42y=0,a23x+a43y=0

(6)

的解.

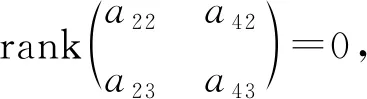
令子空間L1=span(x1),L2=span(x2,x3),α1=α|L1≠0,α2=α|L2=0, 則(L1,[,],α1)和(L2,[,],α2)都是(L,[,],α)的理想, 即有

[x1,x3]=x2, [x2,x2]=a32x2, [x2,x3]=a52x2, [x3,x3]=a62x2.

易驗證當a32,a52不全為0時, 所得的Hom-Jacobi-Jordan代數不是Jacobi-Jordan代數.

2) 對B6, 由于α是自同態, 即α([xi,xj])=[α(xi),α(xj)](i,j=1,2,3), 可得a21=a31=a41=a51=a61=a33=0,a11=a32.由x1,x2,x2滿足Hom-Jacobi等式, 可得a32=0, 進而有a11=0.由x1,x2,x3滿足Hom-Jacobi等式, 可得a53=0.再由其他元素滿足Hom-Jacobi等式, 可得a52a13=a52a23=a52a43=a52a63=0.

① 若a52≠0, 則有a13=a23=a43=a63=0.再經過適當的基變換, 可得[x1,x1]=a12x2, [x2,x3]=x2, 其他括積均為0.易驗證x2,x3,x3不滿足Jacobi等式, 即所得的Hom-Jacobi-Jordan代數不是Jacobi-Jordan代數.

② 若a52=0, 則有[x2,x2]=0, [x2,x3]=0.下面討論a22,a23的取值情況.

(i) 當a22≠0時, 做適當的基變換, 把a12和a42化為0, 則得

[x1,x1]=a13x3, [x1,x2]=a22x2+a23x3(a22≠0),

[x1,x3]=a43x3, [x3,x3]=a62x2+a63x3.

易驗證x1,x1,x2不滿足Jacobi等式.

(ii) 當a22=0,a23≠0時, 做適當的基變換, 把a23化為1,a13和a43化為0, 則可得

[x1,x1]=a12x2, [x1,x2]=x3, [x1,x3]=a42x2, [x3,x3]=a62x2+a63x3.

易驗證當a12,a42,a62,a63不全為0時, 所得的Hom-Jacobi-Jordan代數不是Jacobi-Jordan代數.

(iii) 當a22=a23=0時, 討論a42,a43, 分別可得不是Jacobi-Jordan代數的Hom-Jacobi-Jordan代數

[x1,x1]=a12x2, [x1,x3]=a42x2+a43x3(a43≠0), [x3,x3]=a62x2+a63x3,

[x1,x1]=a13x3, [x1,x3]=x2, [x3,x3]=a62x2+a63x3(a13,a63不全為0),

[x1,x1]=a12x2+a13x3, [x3,x3]=a62x2+a63x3(a63≠0或者a13a62≠0).

證畢.