不同階次下分數階SIR傳染病模型的穩定性分析

錢 蓉, 肖 敏, 王 璐

(南京郵電大學 自動化學院, 人工智能學院, 南京 210023)

0 引 言

傳染病的傳播嚴重威脅人類的生命安全, 如目前全球傳染規模最大的COVID-19(corona virus disease 2019, 新型冠狀病毒肺炎). 由于傳染病的研究不能通過大規模的實驗進行, 因此建立具有傳染病典型特征的數學模型, 進行傳染病動力學分析, 探索傳染病傳播規律, 并預測其發展趨勢是對傳染病進行預防和控制的有效方法之一[1]. 自Kermack等[2]提出經典的SIR(susceptible-infected-removed)模型以來, SIR傳染病模型在傳染病動力學分析中備受關注. 時滯對系統動力學有較大影響, 其可以破壞系統的穩定性, 誘發更復雜的動力學行為, 如周期振蕩、 分岔或混沌[3]. 在多數情況下, 傳染病患者康復后會產生抗體, 再次感染的機率很小, 因此本文研究的SIR模型考慮患者康復后不再受到感染, 主要研究病毒潛伏期時滯的影響.

分數階微積分是由經典微積分到非整數階微積分的推廣[4], 近年來, 因其在化學、 混沌和分形、 控制系統等領域中的應用而受到廣泛關注[5], 分數階微分方程為描述各種過程的記憶和遺傳特性提供了一個強有力的工具[6]. 文獻[7]研究了一類時滯分數階捕食者-食餌模型, 以時滯為分岔參數討論了該模型的Hopf分支問題； 文獻[8]基于一類分數階生態流行病學模型, 研究了該模型解的性質和平衡點的穩定性. 但目前已有的分數階傳染病模型研究都假設分數階次一致, 未進一步考慮不同階次下分數階傳染病模型的動力學性質. 而階次不一致的分數階系統在控制領域已得到廣泛關注[9], 研究表明, 不同階次的分數階系統中存在更多的自由度[10], 使系統的動力學行為更復雜. 目前大多數研究者在建立傳染病模型時都假設易感者人數為一個恒定輸入, 但一旦爆發疫情, 各地區的易感人群數量不會是恒定增長的, 因此本文假設易感人群數量滿足Logistic增長, 更符合實際意義[11]. 由于單位時間內一個感染者接觸到易感者的數量有限, 故傳統建模中采用的標準傳染率和雙線性傳染率[12]不能準確描述傳染病的傳播特性, 因此, 不同形式的非線性傳染率被相繼引入到傳染病模型中[13]. 文獻[14]將飽和傳染率g(I)S引入到傳染病建模中, 為人們研究傳染病模型提供了一種新思路； 文獻[15]引入了一種標準飽和傳染率βSI/(S+I+R), 但并未考慮感染者和易感者接觸的隨機性; 文獻[16]通過引入飽和傳染率βSI/(1+αS), 研究了具有飽和傳染率的分數階SIR傳染病模型的穩定性, 該飽和傳染率不但考慮了感染者聚集對傳染病傳播的影響, 并且通過選取適當的參數α, 可調節感染者和易感者的接觸率.因此, 采用飽和傳染率βSI/(1+αS)建立SIR傳染病數學模型能更好地描述傳染病傳播的實際情況[17]. 本文研究一類具有Logistic增長與飽和傳染率的不同階次分數階時滯SIR傳染病模型的穩定性和分岔分析.

1 預備知識

1.1 分數階導數的定義

目前, 分數階導數定義主要有Riemann-Liouville(R-L)定義、 Caputo定義和Grünwald-Letnikov(G-L)定義. 不同定義下的分數階導數各有特點, 其中Caputo定義允許將分數階方程的初始條件以整數階導數的形式表示, 更適合實際問題的數學建模[18]. 因此本文選取Caputo導數定義處理SIR傳染病模型.

定義1[19]連續函數f(t)的α階Caputo導數定義為

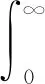
1.2 系統穩定性判據

引理1[20]考慮如下形式的分數階系統：

(1)

其中α∈(0,1],x(t)∈n.如果系統的特征值λi均具有負實部或滿足條件|arg(λi)|>(αiπ)/2, 則系統的平衡點是局部漸近穩定的[21].

α階系統的穩定區域如圖1所示, 因此分數階系統比整數階系統的穩定域更大.

圖1 分數階系統的穩定區域Fig.1 Stable region of fractional-order system

2 模型的建立

文獻[22]研究了一類考慮時滯與飽和傳染率的整數階SIR傳染病模型：

(2)

其中：S(t),I(t),R(t)分別表示t時刻易感者、 感染者和康復者的數量；xS(t)(1-S(t)/y)表示易感患者人數滿足Logistic增長,x表示內在增長率,y表示系統承載力； 時滯τ表示病毒傳播的潛伏期, (mS(t)I(t-τ))/(1+nS(t))表示在t-τ到t時間段內感染的患者數量,m表示病毒傳染率,n表示感染者和易感者的接觸率；a表示感染患者的因病死亡率,b表示傳染病康復率,c表示自然死亡率.由生態學意義可知, 系統(2)所有參數均為非負常數.

相對于傳統模型, 模型(2)綜合考慮了時滯的影響及傳染病傳播的生物學特性.文獻[22]以時滯τ為分岔參數分析了系統(2)的穩定性, 并討論了系統Hopf分岔的存在性. 但這些分析都基于整數階系統, 缺少人口模型的記憶特性. 本文在模型(2)的基礎上, 考慮到Logistic增長與飽和傳染率, 通過引入不同階次下的分數階模型, 建立一類新型時滯SIR傳染病模型：

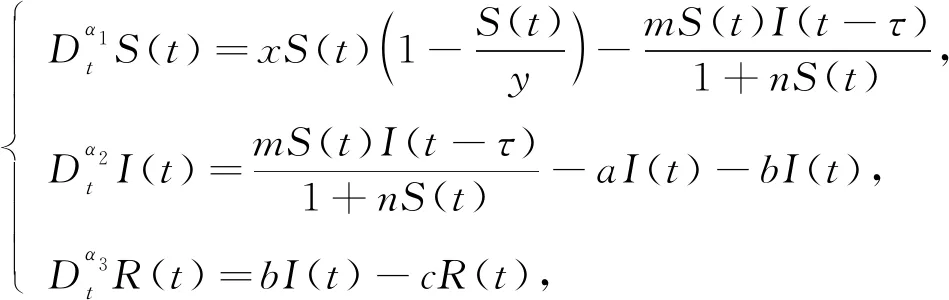
(3)

其中0<αi≤1(i=1,2,3).系統(3)滿足初始條件：S(θ)=φ1(θ)≥0,I(θ)=φ2(θ)≥0,R(θ)=φ3(θ)≥0,θ∈[-τ,0].

3 平衡點及穩定性分析

3.1 系統解的非負性

定理1若S(0),I(0),R(0)是系統(3)的非負初始條件, 則系統(3)的解S(t),I(t),R(t)對所有的t∈[0,+∞)都是非負的.

證明： 根據系統(3)的第一和第二個方程, 結合一階線性方程求解法, 可得

根據系統(3)的第三個方程可得

因此, 若初始條件滿足S(0),I(0),R(0)都是非負數, 則對所有的t∈[0,+∞)系統的可行解都是非負的.

3.2 平衡點的局部穩定性分析

3.2.1 平衡點及基本再生數

平衡點就是當改變系統變量時, 系統狀態不隨其變化的時刻.因此分數階系統平衡點的定義和整數階一致.以系統(1)為例, 分數階系統的平衡點通過求解f(t,x(t))=0計算.

計算求得系統(3)的平衡點為E=(S′,I′,R′), 其中平凡平衡點為E0=(0,0,0), 無病平衡點為E1=(y,0,0), 地方病平衡點為E2=(S*,I*,R*), 且

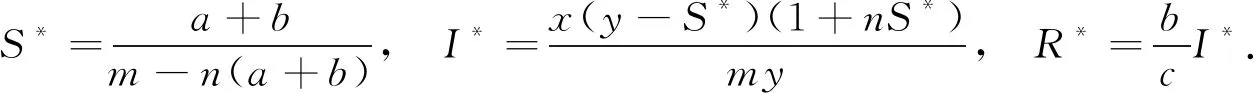
(4)

基本再生數R0是決定傳染病能否得到控制的閾值, 根據感染倉理論可知,R0只與身體內攜帶病毒的感染者數量I(t)有關, 本文采用文獻[23]中的第二代生成矩陣法計算得到無病平衡點E1處的基本再生數.再生矩陣

其在無病平衡點E1=(y,0,0)處的Jacobi矩陣為

因此系統(3)的基本再生數為

定理2若R0>1, 則系統(3)存在唯一的地方病平衡點E2=(S*,I*,R*)； 若R0<1, 則系統(3)不存在地方病平衡點.

證明： 由于地方病平衡點滿足式(4), 所以當R0>1時,my>(1+ny)(a+b)>ny(a+b), 即m>n(a+b), 從而可知S*>0, 對于I*考慮

顯然此時I*>0,R*>0, 即系統(3)存在唯一的地方病平衡點； 而當R0<1時,S*<0, 即系統(3)不存在地方病平衡點.證畢.

3.2.2 無病平衡點的局部穩定性分析

由于本文模型中康復患者的數量R(t)對易感人群的數量S(t)和已感染人群的數量I(t)均無影響, 系統的動力學行為主要由系統(3)的前兩個方程決定, 因此為討論方便, 本文將系統(3)簡化為

(5)

為分析系統的局部漸近穩定性, 將系統(5)線性化得到平衡狀態下的線性系統：

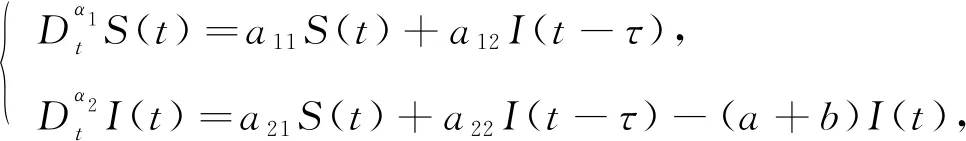
(6)

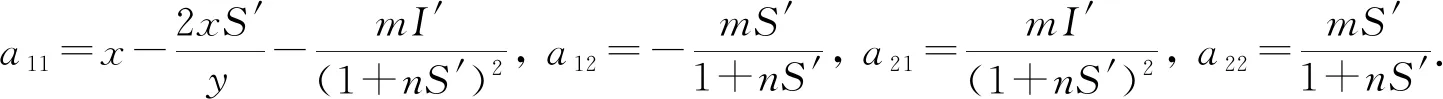
令S1(t)=S(t)-S′,I1(t)=I(t)-I′, 將系統(6)的平衡點移動到原點, 并進行Laplace變換, 得

(7)

其中L[f(t)]表示對f(t)的Laplace變換.系統(7)可以寫成如下形式：

(8)

其中

令det(Δ(s))=0可得系統(3)的特征方程為

μ1(s)+μ2(s)e-sτ=0,

(9)

其中μ1(s)=sα1+α2+(a+b)sα1-a11sα2-a11(a+b),μ2(s)=-a22sα1-a12a21+a11a22.

將平凡平衡點E0=(0,0,0)代入方程(9)計算可得特征方程為

(λ1-x)(λ2+a+b)=0,

(10)

其中λ1=sα1,λ2=sα2,x,a,b均為是非負數.顯然平凡平衡點E0=(0,0,0)是一個不穩定的鞍點.所以本文下面主要討論無病平衡點E1=(y,0,0)和地方病平衡點E2=(S*,I*,R*)的穩定性.

定理3若R0<1, 則當τ=0時, 系統(3)的無病平衡點E1=(y,0,0)是局部漸近穩定的.

證明： 計算可得系統(3)在無病平衡點E1=(y,0,0)處的特征方程為

(11)

當τ=0時, 方程(11)轉化為

(12)

令λ1=sα1,λ2=sα2, 系統的特征根為

λ1=-x,λ2=my/(1+ny)-(a+b)=(a+b)(R0-1),

顯然可知, |arg(λ1)|=π>α1π/2.當R0<1時, |arg(λ2)|=π>α2π/2, 根據引理1可知, 系統(3)的無病平衡點E1局部漸近穩定, 證畢.

定理4若R0<1, 則對任意的τ≥0, 系統(3)的無病平衡點E1=(y,0,0)是局部漸近穩定的.

證明： 當R0<1時, 定理3成立.因為方程(11)中只有sα2含有時滯項, 因此只需考慮當τ>0時, 方程

(13)

根的分布情況.假設方程(13)存在一對純虛根s1,2=±iω(ω>0), 將s1=iω代入方程(13)得

(14)

對方程(14)分離實部、 虛部可得

(15)

將式(15)兩邊平方并相加整理可得

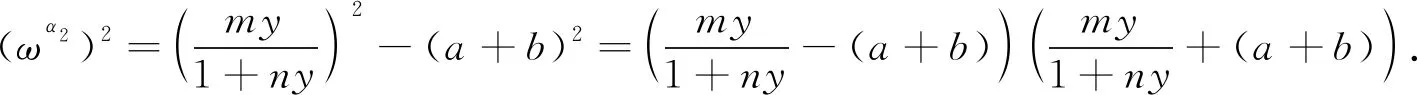
(16)

顯然, 當R0<時式(16)不成立, 即方程(13)不存在純虛根, 再結合定理3及特征根關于時滯的連續性可知, 當R0<時, 對于任意的τ≥0, 系統(3)的無病平衡點E1都是局部漸近穩定的.證畢.

注1定理4表明, 當基本再生數R0<時, 時滯對系統(3)的穩定性無影響.

3.2.3 地方病平衡點的局部穩定性分析

根據方程(9)可知, 地方病平衡點E2=(S*,I*,R*)處的特征方程為

sα1+α2+(a+b)sα1-a11sα2-a11(a+b)+(-a22sα1-a12a21+a11a22)e-sτ=0.

(17)

定理5若α1,2∈(0,1],R0>1, 則當τ=0,a11<0且a+b-a22>0時, 系統(3)的地方病平衡點E2局部漸近穩定.

證明： 由定理2可知, 當R0>1時, 系統(3)才存在地方病平衡點, 且當時滯τ=0時, 特征方程(17)可以改寫為

sα1+α2+(a+b-a22)sα1-a11sα2-a11(a+b)-a12a21+a11a22=0.

(18)

由于無法通過直接計算得到方程(18)的根, 所以本文采用反證法, 證明該特征方程的特征根均具有負實部.

首先, 將s=0代入特征方程(18), 等式不成立, 即特征方程(18)沒有零根.

其次, 假設特征方程(18)有正實根或純虛根記為Xeθi, 其中X>0,θ∈[-π/2,π/2].將s=Xeθi代入方程(18), 并分離實部和虛部, 得

Xα1+α2[sin(θα1+θα2)]+(a+b-a22)Xα1sin(θα1)-a11Xα2sin(θα2)=0,

(20)

分析方程(20)發現： 三項正弦函數前系數滿足Xα1+α2>0, (a+b-a22)Xα>0, -a11Xα>0.因此方程(20)左側公式的符號和sinθ符號一致.

當且僅當θ=0時方程(20)成立, 將θ=0代入方程(19),a12a21=-m2SI/(1+nS)3<0, 可得

Xα1+α2+(a+b-a22)Xα1-a11Xα2-a11(a+b-a22)-a12a21>0,

即θ=0不滿足方程(19).方程組(19)-(20)無解, 原假設不成立, 即特征方程(18)沒有正實部根或純虛根.再結合引理1, 結論得證.

3.3 Hopf分岔

本文選取時滯τ為分岔參數討論系統地方病平衡點的分岔情況.根據Hopf分岔定理[24]可知, 若使系統發生Hopf分岔, 則需系統在平衡點處對應的特征方程有一對共軛復根ρ(τ)±iω(τ), 且在τ=0時該共軛復根滿足ρ(0)=0,ω(0)=ω0>0, 并滿足橫截條件ρ′≠0, 即ρ(τ)±iω(τ)軌跡在τ=τ0處橫穿虛軸.

定理6若R0>1,a11<0,a+b-a22>0,ω存在且P1Q1+P2Q2>0成立, 則：

1) 當τ<τ0時, 系統(3)的地方病平衡點E2是局部漸近穩定；

2) 當τ>τ0時, 系統(3)的地方病平衡點E2不穩定, 即系統(3)在τ=τ0附近發生Hopf分岔.

證明： 假設當τ≥0時, 特征方程(9)存在一對純虛根s1,2=±iω(ω>0), 將s=iω=ωe(πi)/2代入方程(9), 得

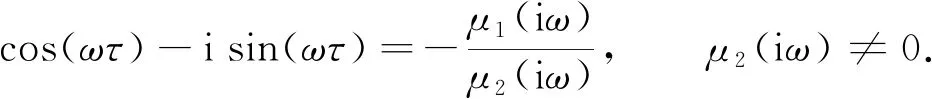
(21)

對式(21)進行實部和虛部的分離, 得

(22)

其中Re[μk(iω)]和Im[μk(iω)]分別表示μk(iω)(k=1,2)的實部和虛部, 并且

將特征方程(9)對τ求導驗證橫截條件：

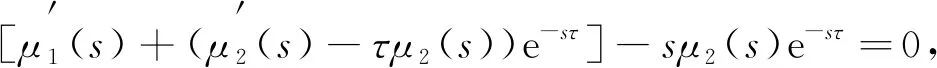
(23)

從而可得

(24)

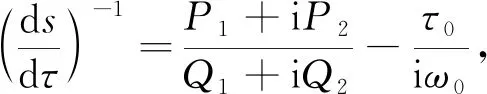
(25)

其中

因此可知

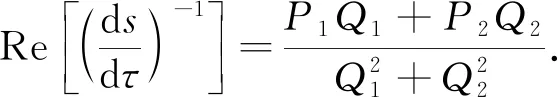
(26)

令f1(ω)=cos(ωτ),f2(ω)=sin(ωτ), 則

(27)

假設方程(27)有正實根, 結合方程(22)可得分岔閾值表達式為

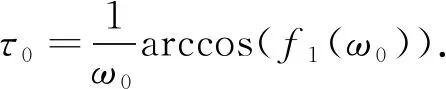
(28)

系統(3)的地方病平衡點E2在τ=τ0處發生Hopf分岔, 根據定理5及特征根關于時滯τ的連續性可知: 當τ<τ0時, 系統(3)的地方病平衡點E2漸近穩定； 當τ>τ0時, 系統(3)的地方病平衡點E2不穩定.證畢.

注2由分岔閾值τ0的表達式可知,τ0隨著分數階次αi的變化而變化, 即分數階次的改變會影響系統的動力學行為.

4 數值模擬和仿真實驗

下面利用MATLAB工具進行數值模擬和仿真實驗.首先給出模型(2)的相關參數, 此時系統為

(29)

根據系統(29)計算可得R0=0.865<1, 且系統僅存在一個無病平衡點E(1,0,0).選取3組不同的時滯參數τ1=0.5,τ2=1.5,τ3=2.5, 系統分數階次分別取α1=0.7,α2=0.99,α3=0.9.由定理4可知, 無病平衡點E1在任意時滯τ≥0下都是局部漸近穩定的, 如圖2所示.

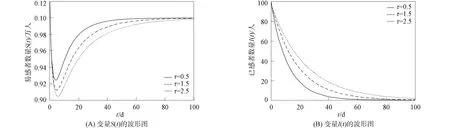
圖2 系統(29)在無病平衡點E1處的全時滯漸近穩定性Fig.2 Asymptotic stability of system (29) at disease-free equilibrium point E1 with full time delay

為驗證地方病平衡點E2在時滯τ=0的穩定性, 根據生態學理論重新調整參數得到系統

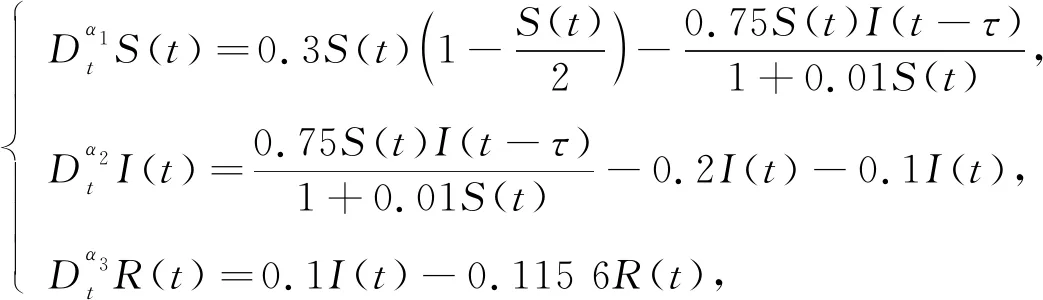
(30)

其仿真結果如圖3所示.根據系統(30)計算可得R0=4.9>1, 且系統存在唯一的地方病平衡點E2=(0.401 6,0.320 9,0.277 5).顯然系統(30)參數滿足a+γ-a22=0.000 01>0,a11=-0.06<0.取模型分數階次α1=0.8,α2=0.99,α3=0.9, 在時滯τ=0的情形下, 由定理5可知, 系統(30)的地方病平衡點E2是局部漸近穩定的.

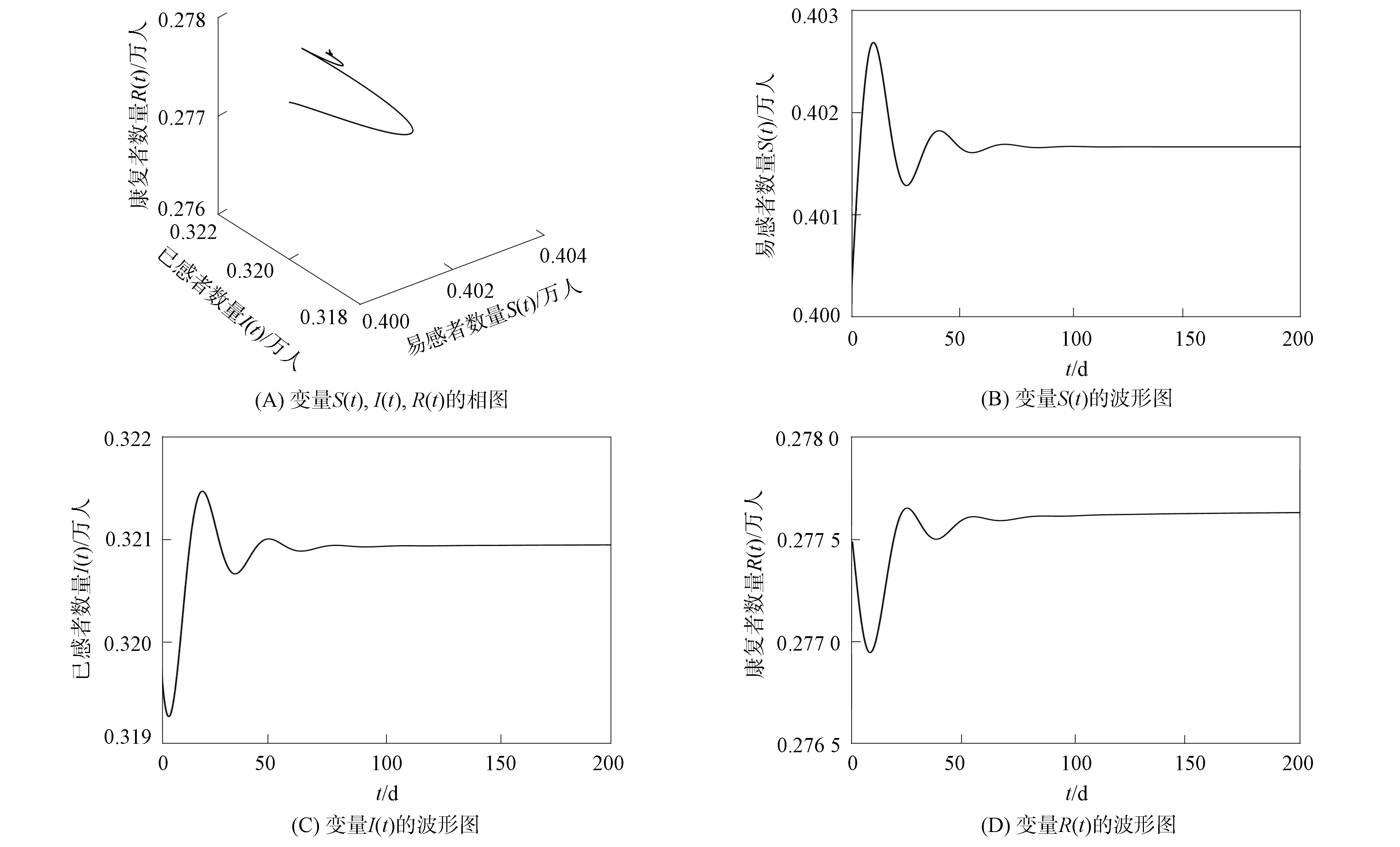
圖3 當τ=0時系統(30)地方病平衡點E2的漸近穩定性Fig.3 Asymptotic stability of system (30) at endemic equilibrium point E2 when τ=0

由Hopf分岔的討論可知, 系統(30)發生Hopf分岔的閾值τ0=5.554.選取時滯參數τ=10, 根據定理6中2)可知, 系統(30)的地方病平衡點E2不穩定, 如圖4所示； 選取時滯參數τ=5, 根據定理6中1)可知, 系統(30)的地方病平衡點E2是局部漸近穩定的, 如圖5所示.

圖4 當τ=10時系統(30)地方病平衡點E2的不穩定性Fig.4 Instability of system (30) at endemic equilibrium point E2 when τ=10

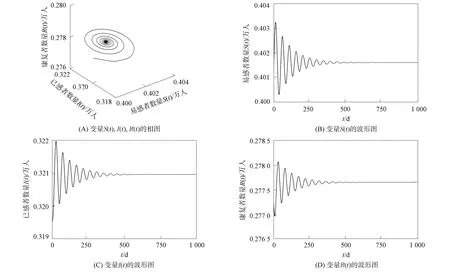
圖5 當τ=5, α1=0.8時系統(30)地方病平衡點E2的漸近穩定性Fig.5 Asymptotic stability of system (30) at endemic equilibrium point E2 when τ=5, α1=0.8

為突出階次不一致分數階系統動力學行為的復雜性, 本文假設系統(30)的分數階次α2=0.99,α3=0.9,τ=5.取α1=0.8, 如圖5所示, 系統(30)的地方病平衡點E2是局部漸近穩定的； 但當取α1=0.9時, 如圖6所示, 系統(30)的地方病平衡點E2開始不穩定了.這主要是因為改變分數階次αi會導致系統分岔閾值發生變化.當α1=0.8時, 系統(30)的分岔閾值τ0=5.554； 當α1=0.9時, 系統(30)的分岔閾值τ0=4.129.

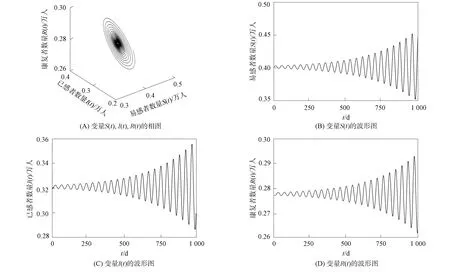
圖6 當τ=5, α1=0.9時系統(30)地方病平衡點E2的不穩定性Fig.6 Instability of system (30) at endemic equilibrium point E2 when τ=5, α1=0.9

為進一步分析分數階次對系統(30)動力學的影響, 固定分數階次α3=0.9不變.先選擇分數階次α2=0.99, 考察分數階次α1與系統分岔閾值τ0之間的關系； 然后選擇分數階次α1=0.9, 考察分數階次α2與系統分岔閾值τ0之間的關系.

當α2=0.99,α3=0.9時, 由圖7(A)可見, 隨著分數階次α1的增大, 分岔閾值τ0增大, 系統(30)的穩定性增強； 當α1=0.9,α3=0.9時, 由圖7(B)可見, 隨著分數階次α2的增大, 分岔閾值τ0減小, 表明系統(30)的穩定性減弱.

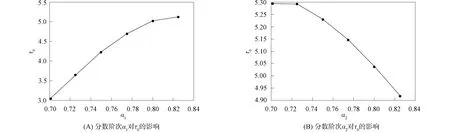
圖7 分數階次α1,α2對系統(30)分岔閾值τ0的影響Fig.7 Effects of fractional orders α1,α2 on bifurcation threshold τ0 of system (30)

綜上所述, 本文首先研究了一類具有Logistic增長與飽和傳染率的不同階次分數階SIR傳染病模型. 通過公式推導得到了R0<1時系統(3)的無病平衡點E1是全時滯漸近穩定的, 給出了系統(3)地方病平衡點E2局部漸近穩定的充分條件, 并結合Hopf分岔定理給出了系統(3)產生Hopf分岔的充分條件及分岔閾值τ0的數學表達式. 其次， 采用MATLAB工具對本文研究的SIR傳染病模型進行了數值仿真, 仿真結果證明了理論分析的正確性. 研究表明, 引進分數階提高了系統的穩定性, 時滯和不同階次分數階使得SIR傳染病模型的動力學行為更復雜, 在某些情況下隨著分數階次的改變, 系統的穩定性也隨之改變.