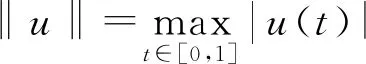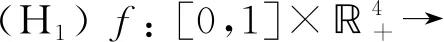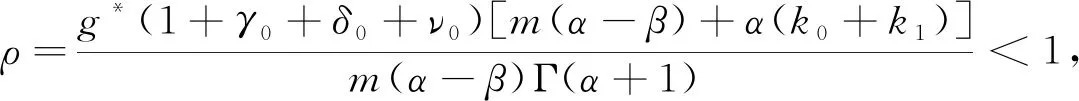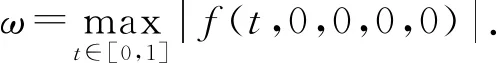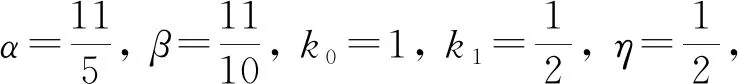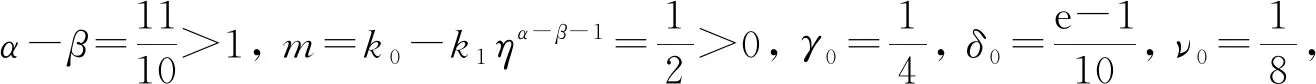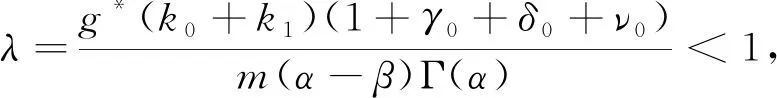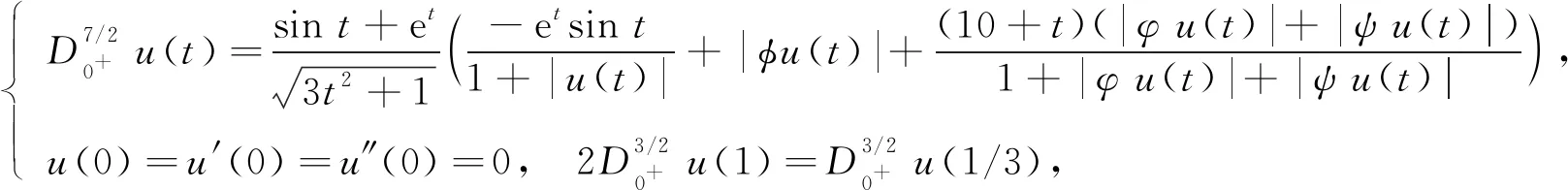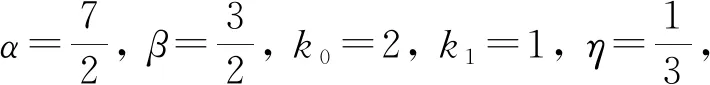一類(lèi)非線性分?jǐn)?shù)階積分微分方程解的存在性與模擬仿真
孫文超, 蘇有慧, 孫 愛(ài)
(1. 沈陽(yáng)工業(yè)大學(xué) 理學(xué)院, 沈陽(yáng) 110870; 2. 徐州工程學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 江蘇 徐州 221018)
0 引 言
微分方程問(wèn)題在物理、 化學(xué)、 生物和工程等領(lǐng)域應(yīng)用廣泛[1-5], 目前, 關(guān)于分?jǐn)?shù)階微分方程解的存在性研究已有很多結(jié)果[6-12]. 但實(shí)際問(wèn)題中抽象出的方程通常可能是較復(fù)雜的且含有積分的分?jǐn)?shù)階微分方程, 如擴(kuò)散過(guò)程、 封閉系統(tǒng)中種群增長(zhǎng)的Volterra模型及控制理論等[13-16]. 因此, 研究分?jǐn)?shù)階積分微分方程尤為重要.
文獻(xiàn)[14]研究了如下分?jǐn)?shù)階積分微分方程正解的存在性:
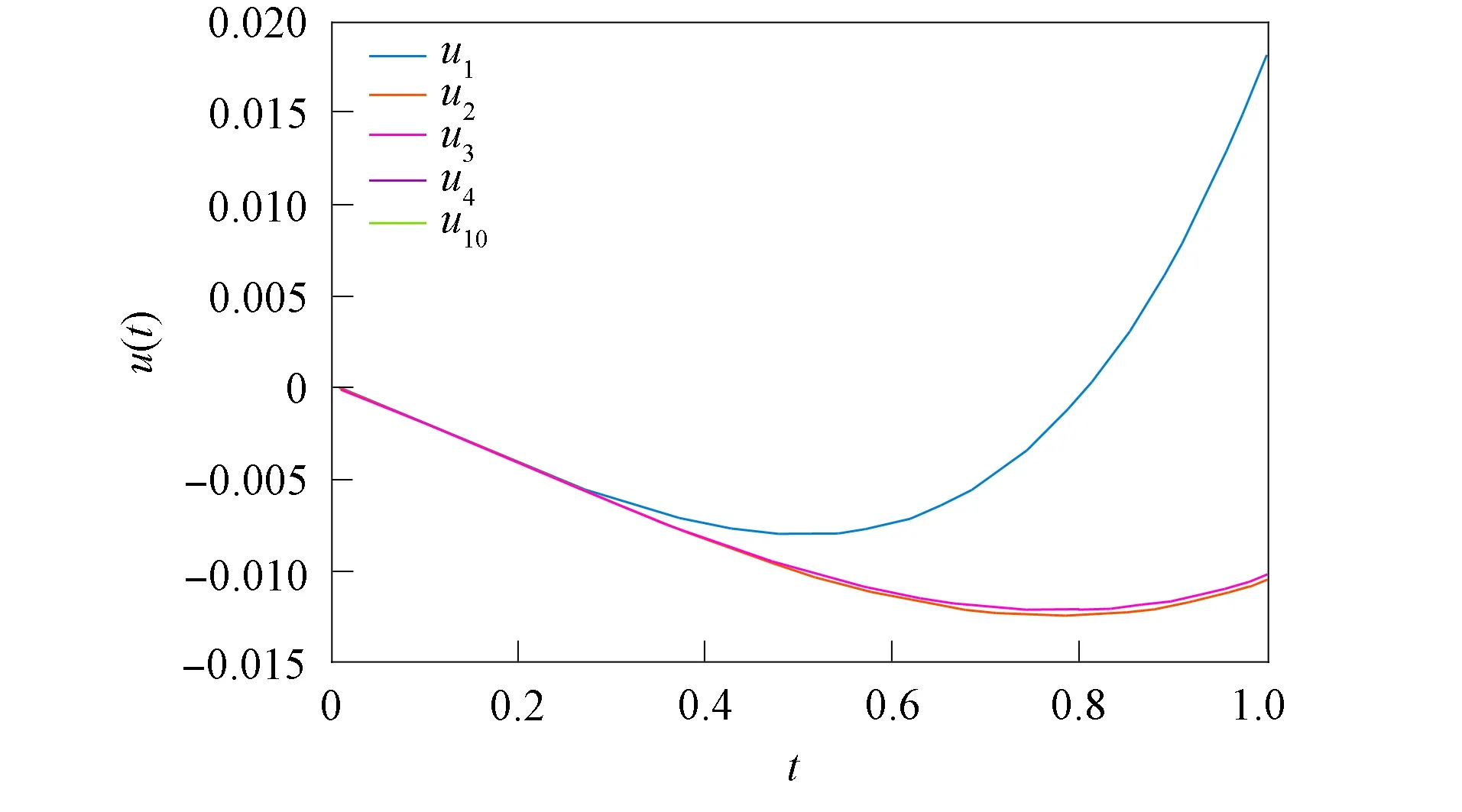
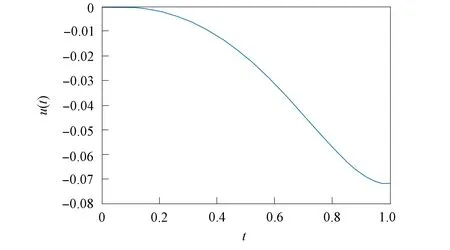
得到了其解的存在性和唯一性結(jié)果, 其中:n-1<α≤n, 0<μ 使用Krasnoselskii不動(dòng)點(diǎn)定理, 得到了其至少存在一個(gè)解的結(jié)果, 其中: 1<α≤2, 0<β≤1;f: [0,1]×3→是連續(xù)的; 定義映射但上述結(jié)果都只從理論方面研究了分?jǐn)?shù)階積分微分解的存在性, 關(guān)于其數(shù)值解方面的研究目前報(bào)道較少[17-18].基于此, 本文考慮如下非線性分?jǐn)?shù)階積分微分方程: (1) 且滿足 通過(guò)使用Banach壓縮映射原理和Krasnoselskii不動(dòng)點(diǎn)定理, 給出分?jǐn)?shù)階積分微分方程(1)至少存在一個(gè)解和存在唯一解的結(jié)論.特別地, 通過(guò)模擬仿真實(shí)例說(shuō)明本文主要結(jié)果的正確性. 定義1[19]令α>0, 函數(shù)u: (0,+∞)→的Riemann-Liouville分?jǐn)?shù)階積分定義為 其中等式右端在(0,+∞)上有定義. 定義2[19]令α>0, 函數(shù)u: (0,+∞)→的Riemann-Liouville分?jǐn)?shù)階導(dǎo)數(shù)定義為 其中n-1≤α 引理1[20]令α>0, 則有分?jǐn)?shù)階微分方程 這里Ci∈,i=1,2,…,n,n=[α]+1. 引理2假設(shè)y∈C[0,1]且n-1<α (2) 有唯一解 (3) 這里m=k0-k1ηα-β-1>0. 證明: 根據(jù)引理1, 有 由u(0)=u′(0)=…=u(n-2)(0)=0, 可得 C2=C3=…=Cn-2=0, 因此 (4) 進(jìn)一步可得 (5) 將式(5)代入式(4)即可推出式(3). 引理3(Krasnoselskii不動(dòng)點(diǎn)定理)[21]設(shè)X是Banach空間E中的非空閉子集, 映射A,B滿足如下條件: 1) 當(dāng)x,y∈X時(shí),Ax+By∈X; 2)A是連續(xù)且緊的; 3)B是一個(gè)壓縮映射. 則存在z∈X, 使得z=Az+Bz. 假設(shè): (H3) 存在一個(gè)常數(shù)b∈(0,α-n+1)和非負(fù)函數(shù)g(t)∈L1/b([0,1],(0,+∞)), 使得對(duì)任意的t∈[0,1],u,x,y,z,u′,x′,y′,z′∈, 均有 |f(t,u,x,y,z)-f(t,u′,x′,y′,z′)|≤g(t)(|u-u′|+|x-x′|+|y-y′|+|z-z′|). 定理1假設(shè)條件(H1)~(H3)成立, 且存在一個(gè)常數(shù)ρ, 如果 (6) 則邊值問(wèn)題(1)有唯一解. 證明: 定義算子A:X→X為 令ΩR={u∈X: ‖u‖ 1) 對(duì)任意的u∈ΩR,Au∈ΩR. 對(duì)u∈?ΩR, 有 因此‖Au‖≤R, 從而A:ΩR→ΩR. 2)A是壓縮映射. 對(duì)任意的u,v∈ΩR,t∈[0,1], 有 因此, |Au(t)-Av(t)|≤ρ‖u-v‖, 故A在ΩR上是壓縮映射.根據(jù)Banach壓縮映射原理可知, 邊值問(wèn)題(1)有唯一解. 例1考慮邊值問(wèn)題: (9) 根據(jù)定理1可知, 分?jǐn)?shù)階積分微分方程(9)有唯一解. 下面用迭代法對(duì)邊值問(wèn)題(9)進(jìn)行模擬仿真, 并給出其迭代過(guò)程曲線與逼近解.令 θ(t)=f(t,u(t),φu(t),φu(t),ψu(yù)(t)), (10) 其中 取初始值 迭代公式為 邊值問(wèn)題(9)的迭代過(guò)程如圖1所示.由圖1可見(jiàn), 其迭代過(guò)程是收斂的.圖2是邊值問(wèn)題(9)經(jīng)過(guò)10次迭代后的逼近解.由圖2可見(jiàn), 分?jǐn)?shù)階積分微分方程(9)有唯一解. 圖1 邊值問(wèn)題(9)的迭代過(guò)程Fig.1 Iterative process of boundary value problem (9) 圖2 邊值問(wèn)題(9)的逼近解Fig.2 Approximate solution of boundary value problem (9) 定理2假設(shè)條件(H1)~(H3)成立, 并且存在一個(gè)常數(shù)λ, 使得 (11) 則邊值問(wèn)題(1)在X中至少存在一個(gè)解. 證明: 先將ΩR上的映射A分成A1和A2, 其中 下面分為三步證明. 1) 對(duì)任意的x,y∈ΩR, 有A1x+A2y∈ΩR. 根據(jù)式(7)中倒數(shù)第二個(gè)不等式, 可得 對(duì)任意的x,y∈ΩR,t∈[0,1], 有 因此,A1x+A2y∈ΩR. 2)A1是連續(xù)且緊的. 首先, 證明A1在ΩR上一致有界.顯然, 根據(jù)式(7)倒數(shù)第二個(gè)不等式的前兩項(xiàng), 有 因此, 對(duì)任意的u∈ΩR,A1在ΩR上一致有界. 其次, 證明A1是等度連續(xù)的.由于f是連續(xù)的, 易知A1也是連續(xù)的.令u∈ΩR,t1,t2∈[0,1], 且 可得 因此, 如果t2→t1, 則有 |(A1u)(t2)-(A1u)(t1)|→0, 故A1是等度連續(xù)的.根據(jù)Arzela-Ascoli定理可知,A1在ΩR中是連續(xù)且緊的. 3)A2是一個(gè)壓縮映射. 對(duì)任意的u,v∈ΩR,t∈[0,1], 根據(jù)假設(shè)條件(H3), 有 由式(11)可知,A2是一個(gè)壓縮映射.因此, 引理3所有的條件都滿足, 故邊值問(wèn)題(1)至少存在一個(gè)解. 例2考慮邊值問(wèn)題: (12) 根據(jù)定理2可知, 分?jǐn)?shù)階積分微分方程(12)至少存在一個(gè)解. 下面利用迭代法對(duì)邊值問(wèn)題(12)進(jìn)行模擬仿真, 并給出其迭代過(guò)程曲線與逼近解.令θ(t)定義如式(10), 其中 取初始值 迭代公式為 邊值問(wèn)題(12)的迭代過(guò)程如圖3所示.由圖3可見(jiàn), 其迭代過(guò)程收斂.圖4是邊值問(wèn)題(12)經(jīng)過(guò)15次迭代后的逼近解.由圖4可見(jiàn), 分?jǐn)?shù)階積分微分方程(12)至少存在一個(gè)解. 圖4 邊值問(wèn)題(12)的逼近解Fig.4 Approximate solution of boundary value problem (12)
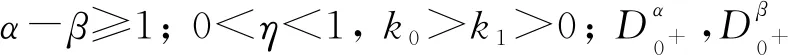
1 預(yù)備知識(shí)
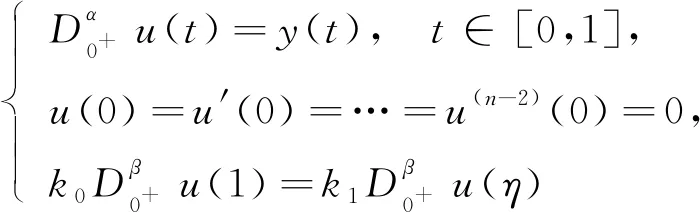

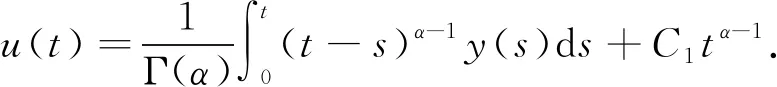
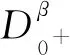

2 主要結(jié)果