旋轉(zhuǎn)直驅(qū)閥的雙閉環(huán)模糊PID控制仿真分析

鄧新陽(yáng), 李 偉, 胡春艷, 王 銳, 李海濤

(1. 中國(guó)科學(xué)院 工程熱物理研究所, 北京 100089； 2. 中國(guó)科學(xué)院大學(xué) 工程科學(xué)學(xué)院, 北京 101400)

在傳統(tǒng)航空發(fā)動(dòng)機(jī)燃油系統(tǒng)中, 通常采用電液伺服閥或者步進(jìn)電機(jī)驅(qū)動(dòng)計(jì)量活門開度. 但電液伺服閥結(jié)構(gòu)復(fù)雜, 加工困難, 同時(shí)對(duì)工作液的清潔要求較高, 而步進(jìn)電機(jī)存在齒輪空回等問題, 從而限制了其在航空發(fā)動(dòng)機(jī)中的應(yīng)用. 旋轉(zhuǎn)直驅(qū)閥(rotate direct drive valve, RDDV)沒有尺寸精密的噴嘴擋板及射流管等易堵塞結(jié)構(gòu), 具有結(jié)構(gòu)簡(jiǎn)單、 抗污染能力強(qiáng)、 可靠性高等優(yōu)點(diǎn), 目前已成為伺服閥的主要發(fā)展趨勢(shì)[1-5]. 采用有限轉(zhuǎn)角力矩電機(jī)(limited angle torque motor, LATM)直接驅(qū)動(dòng)閥芯旋轉(zhuǎn), 結(jié)構(gòu)簡(jiǎn)單, 便于安裝和拆卸； 同時(shí)控制器通過電機(jī)直接控制閥口開度, 有利于數(shù)字化控制, 因此旋轉(zhuǎn)直驅(qū)閥在各領(lǐng)域中廣泛應(yīng)用. 但RDDV系統(tǒng)通過電機(jī)直接驅(qū)動(dòng)閥芯旋轉(zhuǎn)的結(jié)構(gòu)不存在限位機(jī)構(gòu), 因此對(duì)控制系統(tǒng)的精度和穩(wěn)定性提出了較高的要求. 同時(shí), 有限轉(zhuǎn)角力矩電機(jī)在驅(qū)動(dòng)計(jì)量活門旋轉(zhuǎn)時(shí), 會(huì)受液動(dòng)力負(fù)載的影響, 因此系統(tǒng)對(duì)負(fù)載適應(yīng)性也提出了較高要求.

目前, 對(duì)電機(jī)的控制通常采用經(jīng)典的比例-積分-微分(PID)控制. 但隨著對(duì)控制性能越來(lái)越高的要求, 傳統(tǒng)的單閉環(huán)PID控制已經(jīng)不能滿足系統(tǒng)的快速性和準(zhǔn)確性要求, 為提高PID控制器的性能, 已提出了很多改進(jìn)方法. 如文獻(xiàn)[6]通過比較電流環(huán)/位置環(huán)和速度環(huán)/位置環(huán)兩種雙閉環(huán)控制器, 提出了采用電流環(huán)+位置環(huán)的結(jié)構(gòu)模式, 有效提高了系統(tǒng)的快速性和靈活性. 但雙閉環(huán)PID控制器仍是線性控制器, 僅在工作點(diǎn)附近才能保持良好的控制性, 若在偏離工作點(diǎn)較遠(yuǎn)的非線性區(qū)域, 則難以保證系統(tǒng)的動(dòng)態(tài)品質(zhì). 因此, 文獻(xiàn)[7]提出了將模糊控制與PID控制相結(jié)合的方法, 解決了傳統(tǒng)PID控制中抗擾動(dòng)能力差的缺點(diǎn), 提高了系統(tǒng)的控制能力.

本文首先建立旋轉(zhuǎn)直驅(qū)閥的數(shù)學(xué)模型, 并通過MATLAB軟件進(jìn)行仿真分析. 在此基礎(chǔ)上, 提出采用位置環(huán)+電流環(huán)的雙閉環(huán)控制系統(tǒng). 電流環(huán)采用PI控制, 在消除噪聲影響的前提下, 保證系統(tǒng)的輸出力矩快速收斂且無(wú)殘差； 位置環(huán)采用PID控制, 并與模糊控制相結(jié)合, 這是因?yàn)槟：?PI控制器對(duì)高階被控過程動(dòng)態(tài)性能較差, 而模糊-PD控制器會(huì)產(chǎn)生較大的穩(wěn)態(tài)誤差. 最后通過系統(tǒng)仿真驗(yàn)證了該控制方法的快速性、 準(zhǔn)確性及負(fù)載適應(yīng)性[7].

1 RDDV系統(tǒng)結(jié)構(gòu)及建模

1.1 RDDV系統(tǒng)結(jié)構(gòu)

RDDV系統(tǒng)結(jié)構(gòu)如圖1所示, 直驅(qū)閥閥芯在有限轉(zhuǎn)角力矩、 電機(jī)輸出力矩和閥芯受到負(fù)載力矩(僅考慮負(fù)載的液動(dòng)力)的共同作用下開始旋轉(zhuǎn), 角位移傳感器將閥芯的實(shí)際角度反饋給控制器, 并與輸入位置信號(hào)做差產(chǎn)生控制信號(hào), 從而實(shí)現(xiàn)對(duì)系統(tǒng)的閉環(huán)控制.

圖1 RDDV伺服系統(tǒng)UG三維效果Fig.1 RDDV servo system UG three-dimensional effect

1.2 有限轉(zhuǎn)角力矩電機(jī)建模

力矩電機(jī)是一種單相的無(wú)刷直流電機(jī), 在輸入電流作用下, 可在一定旋轉(zhuǎn)角度內(nèi)產(chǎn)生驅(qū)動(dòng)力矩, 其等效電路圖如圖2所示. 由圖2可列出電機(jī)各環(huán)節(jié)的微分方程[8].

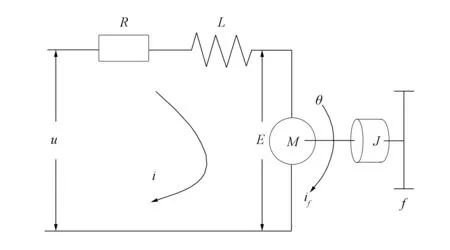
圖2 有限轉(zhuǎn)角力矩電機(jī)的等效電路圖Fig.2 Equivalent circuit diagram of limited-angle torque motor

有限轉(zhuǎn)角力矩電機(jī)電壓平衡方程為

(1)

其中U為電機(jī)控制電壓,R為電機(jī)電樞電阻,i為電流,L為電機(jī)電樞電感,e為電機(jī)反電動(dòng)勢(shì).在不考慮電機(jī)干摩擦且為線性階段時(shí), 機(jī)械系統(tǒng)的力矩平衡方程為

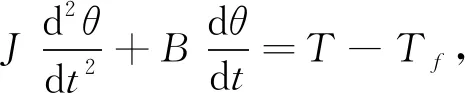
(2)

其中J為轉(zhuǎn)子與閥芯的轉(zhuǎn)動(dòng)慣量,θ為旋轉(zhuǎn)角度,B為黏性阻尼系數(shù),T為電磁轉(zhuǎn)矩,Tf為負(fù)載轉(zhuǎn)矩.額定勵(lì)磁下電樞回路的反電動(dòng)勢(shì)方程為

e=Kbω,

(3)

其中Kb為電機(jī)反電動(dòng)勢(shì)系數(shù),ω為電機(jī)轉(zhuǎn)速.額定勵(lì)磁下電磁轉(zhuǎn)矩方程為

T=Kti,

(4)

其中Kt為電機(jī)電磁轉(zhuǎn)矩常數(shù).

1.3 液動(dòng)力負(fù)載建模

閥芯在工作時(shí)會(huì)受到外部作用力、 慣性力、 阻尼力以及工作介質(zhì)對(duì)閥芯的作用力.外部作用力即電機(jī)驅(qū)動(dòng)閥芯運(yùn)動(dòng)的力, 慣性力和阻尼力是由于閥芯具有一定質(zhì)量和運(yùn)動(dòng)時(shí)的阻尼作用而產(chǎn)生的力, 對(duì)于航空發(fā)動(dòng)機(jī)轉(zhuǎn)速控制器, 這兩個(gè)力都很小, 在分析受力時(shí)可忽略不計(jì)[9].工作介質(zhì)對(duì)閥芯的作用力包括液動(dòng)力和側(cè)向液壓力, 其中側(cè)向液壓力常通過在閥芯工作表面沿圓周設(shè)置寬度較小的均壓槽, 以減小其對(duì)閥芯運(yùn)動(dòng)的影響； 而液動(dòng)力根據(jù)其性質(zhì)又分為穩(wěn)態(tài)液動(dòng)力和瞬態(tài)液動(dòng)力[10].

穩(wěn)態(tài)液動(dòng)力Ts是指工作介質(zhì)通過節(jié)流窗口時(shí)流量不變, 由流速大小及方向變化而產(chǎn)生的對(duì)閥芯的作用力[11]：

Ts=2cvμAΔprcosα=Ksθ,

(5)

其中cv為工作介質(zhì)流經(jīng)節(jié)流窗口時(shí)的速度系數(shù),μ為流量系數(shù),A為節(jié)流窗口的節(jié)流面積, Δp為節(jié)流窗口前后的壓力差,r為閥芯半徑,α=69°為射流角,Ks為穩(wěn)態(tài)液動(dòng)力系數(shù).瞬態(tài)液動(dòng)力Tr是指閥芯開度變化時(shí), 流體速度和加速度變化對(duì)閥芯產(chǎn)生的作用力:

(6)

其中W為面積梯度,L為阻尼長(zhǎng)度,Kr為瞬態(tài)液動(dòng)力系數(shù).

1.4 RDDV系統(tǒng)建模

對(duì)式(1)和式(2)進(jìn)行拉氏變換:

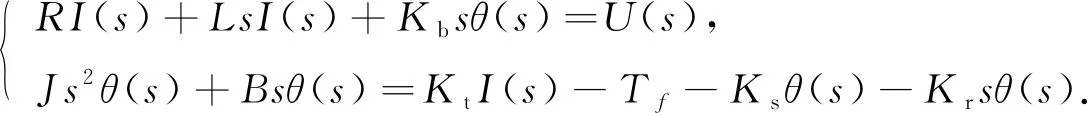
(7)

忽略閥芯所受的機(jī)械摩擦和Coulomb摩擦, 聯(lián)立式(7)得到角位移θ(s)和輸入電壓U(s)的傳遞函數(shù)為

(8)

2 控制器設(shè)計(jì)

為提高系統(tǒng)性能, 通常采用多閉環(huán)控制方法.傳統(tǒng)“三環(huán)”結(jié)構(gòu)能有效改善系統(tǒng)的動(dòng)態(tài)特性, 但由于閉環(huán)數(shù)多, 不能滿足系統(tǒng)的快速性要求.因此, 考慮采用位置環(huán)+速度環(huán)或位置環(huán)+電流環(huán)的雙閉環(huán)結(jié)構(gòu)[12-14].由文獻(xiàn)[6]可知, 位置環(huán)+速度環(huán)系統(tǒng)的負(fù)載適應(yīng)性更好, 而位置環(huán)+電流環(huán)系統(tǒng)快速性更好.根據(jù)需求選取系統(tǒng)快速性更好的位置環(huán)+電流環(huán)結(jié)構(gòu).

2.1 電流環(huán)設(shè)計(jì)

電機(jī)中電流與電動(dòng)機(jī)的輸出力矩成正比, 電流環(huán)的作用是增強(qiáng)系統(tǒng)的抗擾動(dòng)能力, 在無(wú)電流環(huán)時(shí), 系統(tǒng)輸出電流會(huì)隨擾動(dòng)的變化而發(fā)生波動(dòng), 直接影響電機(jī)的輸出力矩, 進(jìn)而影響電機(jī)對(duì)角度或速度的響應(yīng).同時(shí), 在電流環(huán)中需設(shè)置限幅結(jié)構(gòu), 以防止加減速過程中產(chǎn)生的力矩過大.

RDDV有限轉(zhuǎn)角力矩馬達(dá)的繞組可視為電阻R與電感L的串聯(lián)模型, 則繞組電流I(s)和驅(qū)動(dòng)電壓U(s)之間的傳遞函數(shù)[15]為

I(s)/U(s)=1/(Ls+R),

(9)

PI控制的動(dòng)態(tài)方程為

(10)

傳遞函數(shù)為

Gi(s)=Ki[1+1/(Tis)],

(11)

其中Ti為積分時(shí)間常數(shù),ui(t)和ei(t)分別為控制器的輸出、 輸入信號(hào),Ki為控制器比例系數(shù).

考慮到電機(jī)需濾除電樞電流中所有的交流噪聲, 因此電流負(fù)反饋需帶有一階低通濾波, 其表達(dá)式為a/(Tts+1), 其中Tt為濾波時(shí)間常數(shù),a為電流環(huán)反饋系數(shù). 從而可得如圖3所示電流環(huán)的Simulink建模結(jié)構(gòu).

圖3 電流環(huán)閉環(huán)模型Fig.3 Current loop closed-loop model

電流環(huán)的開環(huán)傳遞函數(shù)為

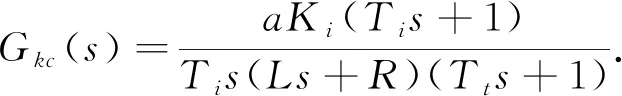
(12)

為使控制回路盡可能簡(jiǎn)單, 本文采用零極點(diǎn)對(duì)消的方法選取電流環(huán)的積分時(shí)間常數(shù)為

Ti=L/R.

(13)

從而開環(huán)傳遞函數(shù)為

(14)

閉環(huán)傳遞函數(shù)為

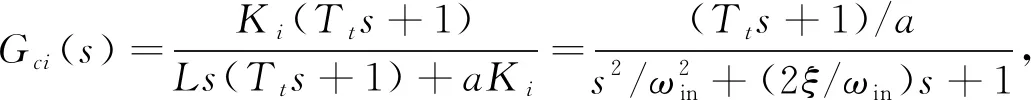
(15)

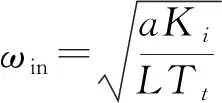
取反饋系數(shù)為a=1,Tt=0.000 1 s[15]. 選取不同的Ki值, 使得電流環(huán)的截止頻率在500 Hz附近, 經(jīng)過調(diào)試, 選取Ki=6. 圖4為電流環(huán)閉環(huán)Bode圖. 由圖4可見, 系統(tǒng)帶寬為484 Hz, 滿足設(shè)計(jì)要求.

圖4 電流環(huán)閉環(huán)Bode圖Fig.4 Current loop closed-loop Bode diagram

2.2 位置環(huán)設(shè)計(jì)

位置環(huán)作為電機(jī)控制系統(tǒng)的外環(huán), 可直接決定伺服控制系統(tǒng)的動(dòng)態(tài)性能和靜態(tài)性能指標(biāo). 因此, 位置環(huán)應(yīng)采用PID控制器. PID的傳遞函數(shù)[14-15]為

Gpi(s)=Kp[1+1/(Tis)+Tds],

(16)

位置環(huán)的開環(huán)傳遞函數(shù)為

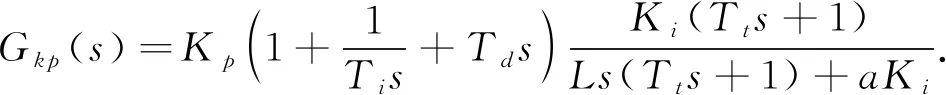
(17)

2.3 模糊控制器設(shè)計(jì)

位置環(huán)采用PID控制方法, 可使系統(tǒng)的動(dòng)態(tài)性能和穩(wěn)態(tài)性得到大幅度提升, 但當(dāng)系統(tǒng)受到液動(dòng)力負(fù)載時(shí), PID的定常參數(shù)無(wú)法適應(yīng)多變的負(fù)載, 因此采用將模糊控制與PID結(jié)合的方法, 使系統(tǒng)既能滿足控制精度高、 響應(yīng)速度快的要求, 又能保證其靈活性和較強(qiáng)的適應(yīng)性.

以角位移誤差E和誤差變化率EC作為輸入, 以控制參數(shù)的變化量ΔKP,ΔKI,ΔKD作為輸出, 采用模糊控制方法對(duì)系統(tǒng)進(jìn)行控制參數(shù)的實(shí)時(shí)整定. 選取7個(gè)模糊語(yǔ)言值, 記為{NB,NM,NS,ZO,PS,PM,PB}, 作為輸入和輸出的模糊狀態(tài)描述, 三角函數(shù)在論域范圍內(nèi)靈敏度較高, 將其選作NM,NS,ZO,PS,PM等中間模糊狀態(tài)的隸屬度函數(shù). 而NB和PB選用高斯形隸屬函數(shù), 以保證系統(tǒng)兩端能平滑過渡. 圖5為模糊控制器隸屬函數(shù)示意圖.

圖5 模糊控制器隸屬函數(shù)示意圖Fig.5 Schematic diagram of membership function of fuzzy controller

根據(jù)文獻(xiàn)[15-16]建立模糊控制規(guī)則, 使系統(tǒng)在不同的輸入條件下, 輸出不同的ΔKP,ΔKI,ΔKD, 從而對(duì)PID控制參數(shù)KP,KI,KD進(jìn)行在線整定. PID中的控制參數(shù)為

KP=KP0+ΔKP,KI=KI0+ΔKI,KD=KD0+ΔKD,

(18)

其中KP0,KI0,KD0為控制參數(shù)的初始值.模糊控制規(guī)則表如圖6所示.

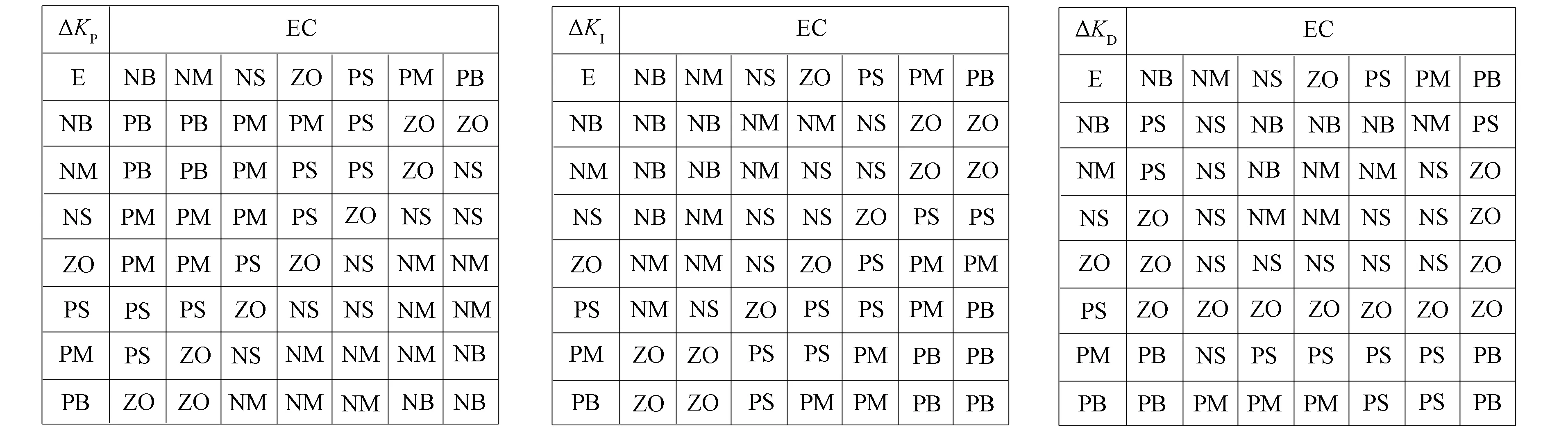
圖6 ΔKP,ΔKI,ΔKD模糊控制規(guī)則表Fig.6 ΔKP,ΔKI,ΔKD fuzzy control rule tables

3 仿真校驗(yàn)

下面利用MATLAB/Simulink軟件搭建旋轉(zhuǎn)直驅(qū)閥模型, 分析其在不同控制方法下的響應(yīng).

3.1 階躍響應(yīng)

分別對(duì)傳統(tǒng)PID、 雙閉環(huán)PID和模糊雙閉環(huán)PID控制器下的旋轉(zhuǎn)直驅(qū)伺服系統(tǒng)輸入一個(gè)階躍信號(hào), 得到響應(yīng)曲線如圖7所示. 由圖7可見, 常規(guī)的PID控制器、 位置/電流雙閉環(huán)控制器和模糊雙閉環(huán)PID控制器在階躍信號(hào)下, 響應(yīng)時(shí)間分別為0.22,0.19,0.02 s, 并且常規(guī)的PID控制會(huì)出現(xiàn)較大的超調(diào)量. 模糊PID控制極大縮短了響應(yīng)時(shí)間, 這是因?yàn)楫?dāng)系統(tǒng)的輸入信號(hào)E較大時(shí), 控制器會(huì)取較大的ΔKP和較小的ΔKI, 在保證系統(tǒng)快速響應(yīng)的基礎(chǔ)上, 防止出現(xiàn)較大的超調(diào)； 當(dāng)E為中間值時(shí), ΔKP會(huì)適量減小, 同時(shí)ΔKI和ΔKD取值適中, 以保證響應(yīng)速度； 當(dāng)E較小時(shí), 為保證系統(tǒng)的穩(wěn)定, ΔKP和ΔKI會(huì)適當(dāng)增大. 因此, 常規(guī)PID控制效果不理想, 模糊雙閉環(huán)控制縮短了調(diào)節(jié)時(shí)間, 改善了控制效果.

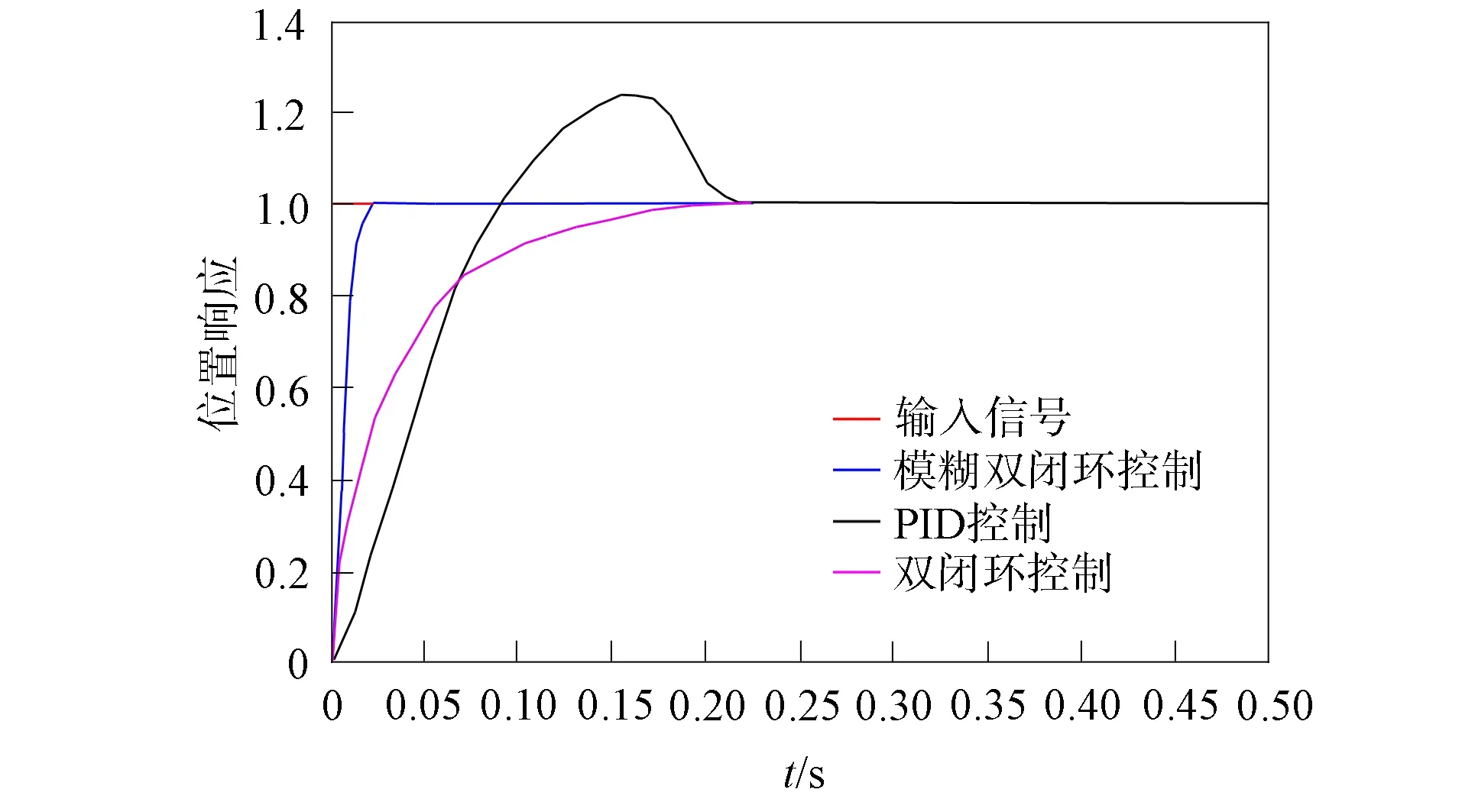
圖7 不同控制器的位置階躍響應(yīng)曲線Fig.7 Position step response curves of different controllers

3.2 正弦響應(yīng)

對(duì)常規(guī)PID控制和模糊PID控制輸入不同頻率的正弦波信號(hào), 響應(yīng)結(jié)果如圖8和圖9所示. 由圖8和圖9可見： 當(dāng)輸入信號(hào)的頻率較低時(shí), 兩種控制方法均具有良好的跟蹤性能； 但當(dāng)系統(tǒng)的輸入信號(hào)頻率較高時(shí), 常規(guī)PID控制方法出現(xiàn)明顯的超調(diào), 并且大幅度滯后, 而模糊PID控制雖然有小幅度滯后, 但響應(yīng)速度明顯更快, 并且無(wú)超調(diào)量, 其動(dòng)態(tài)跟蹤特性明顯優(yōu)于常規(guī)PID控制. 這是因?yàn)樵趨?shù)整定過程中, 當(dāng)系統(tǒng)輸出大于給定輸出時(shí), ΔKI會(huì)取小值甚至負(fù)值以減小KI, 保證系統(tǒng)的穩(wěn)態(tài)精度, 系統(tǒng)上升時(shí)間長(zhǎng)于要求時(shí)間時(shí), ΔKI和ΔKP同時(shí)增大, 保證了系統(tǒng)的快速性.

圖8 輸入20 rad/s時(shí)的正弦響應(yīng)曲線Fig.8 Sine response curves at 20 rad/s

圖9 輸入200 rad/s時(shí)的正弦響應(yīng)曲線Fig.9 Sine response curves at 200 rad/s

3.3 系統(tǒng)Bode圖

圖10為采用模糊PID控制時(shí)系統(tǒng)的閉環(huán)Bode圖. 由圖10可見, 當(dāng)頻率的回路增益為-3 dB時(shí), 系統(tǒng)的相位裕度為48.4°, 帶寬為98.3 Hz, 系統(tǒng)閉環(huán)穩(wěn)定.

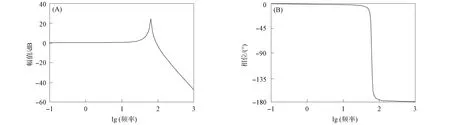
圖10 系統(tǒng)閉環(huán)Bode圖Fig.10 System closed-loop Bode diagram

綜上所述, 為提高旋轉(zhuǎn)直驅(qū)閥的動(dòng)態(tài)特性, 本文通過MATLAB建立了RDDV系統(tǒng)的數(shù)學(xué)模型, 并在此基礎(chǔ)上提出了采用位置環(huán)/電流環(huán)的雙閉環(huán)控制結(jié)構(gòu), 位置環(huán)采用PID控制, 并與模糊控制相結(jié)合, 從而實(shí)現(xiàn)對(duì)PID控制參數(shù)的自整定. 由仿真分析可得如下結(jié)論：

1) 采用模糊PID控制方法可顯著提高系統(tǒng)的響應(yīng)速度, 縮短調(diào)節(jié)時(shí)間；

2) 通過施加負(fù)載擾動(dòng), 系統(tǒng)可在極短的時(shí)間內(nèi)恢復(fù)到正常工作狀態(tài), 因此采用模糊PID控制可有效克服未知擾動(dòng)對(duì)系統(tǒng)性能的影響；

3) 由輸入不同頻率正弦信號(hào)的仿真分析可見, 模糊PID在保證系統(tǒng)無(wú)超調(diào)的前提下, 相位滯后明顯低于常規(guī)PID控制, 具有更好的跟蹤性.