物流配送中心選址問題求解模型優化設計

彭宏春

（上海市現代流通學校，上海 200444）

0 引言

成本是物流企業發展最為關鍵的因素之一，配送中心選址會直接影響配送成本，由此可見，配送中心選址模型的建立以及模型求解算法的選擇至關重要。

隨著物流系統復雜程度的增加，物流配送中心的選址受到越來越多因素的影響，線性規劃、重心法、層次分析法等傳統方法很難得到最優解。為了解決上述傳統分析方法的不足，將智能算法引入物流配送中心選址問題中，如粒子群算法（PSO）、傳統群狼算法（BWPA）等，由于各個選址方法在應用過程中都有一定的局限性，因此，在實際的物流配送中心選址中，需要根據實際情況進行一定的改進優化。本文在進行物流配送中心選址時，基于傳統的群狼算法，再結合分數階模型，從而提升選址的準確性。

群狼算法（WPA）是模仿狼群捕食的過程而建立的算法。狼群在捕食時，各狼具有明確的分工，可分為頭狼、探狼和猛狼，群狼依據頭狼號召、探狼游走和猛狼圍攻的分工協作實現了對獵物的高效圍捕[1]。在基本群狼算法中，徐小平，等[2]為了解決傳統群狼算法在圍攻步長不確定方面的問題，采用擾動操作進行優化改進，從而使算法的精確性大幅度提升。針對群狼算法求解精度較低等缺陷，張惠珍，等[3]引入拉格朗日松弛策略，設計了一種拉格朗日群狼算法，孫冉，等[4]應用群狼算法，重新定義游走、召喚、圍攻等操作以及種群更新策略，有效解決了新型醫療服務體系的構建問題。

目前群狼算法仍處于不斷深化研究階段。本文主要是基于前人的研究成果，采用群狼算法求解物流配送中心選址問題，為了提升最終的求解精度，將分數階模型與群狼算法相結合，從而得到配送中心最優選址。

1 物流配送中心選址模型建立

本文物流配送中心選址的核心目標是降低成本，在選擇的配送中心數量不變的情況下，在一定的區域內選擇最優地址，使整個配送網絡所需的成本降至最低。

根據物流配送中心選址的核心目標，最優地址即是使需求點的需求量與距離值乘積達到最小，目標函數為：

約束條件：

K={1，2,...,n}表示需求點的集合；Mi表示到需求點i的距離小于l的備選配送中心的集合；wi表示需求點i對應的需求量；bij表示需求點i到離它最近配送中心j的距離；zij是0-1變量，當其為1時，表示需求點i的需求量由配送中心j供應，否則zij=0；sj是0-1變量，當其為1時，表示點j被選中，作為配送中心；l表示選中的配送中心到由它配送的需求點的距離上限。式（2）表示配送網絡中每個位置只能由一個配送中心供應；式（3）表示每個需求點所對應的配送中心是唯一的；式（4）表示被選中的配送中心數量為g；式（5）表示變量zij和sj是0-1變量；式（6）確保每個需求點都處于配送區域內。

2 選址模型求解方法分析

2.1 傳統的群狼算法

群狼算法主要是根據群狼的游走、召喚和圍攻三個捕食行為而設計出的一種算法，其中游走行為選擇出目前所在區域的局部最優位置；召喚行為過程中，頭狼會召喚周圍的猛狼去尋找附近區域更優的位置；圍攻行為是群狼對獵物進行圍捕的過程。

群狼算法求解相關問題時，需要經過以下過程：

（1）頭狼的確定。假設群狼擁有的狼數量為N，首先在群狼中隨機選取一頭狼作為頭狼，在求解過程中，實時記錄和對比群狼各個狼的空間位置，將最優目標函數值的狼更新替代為頭狼Ytoulang。頭狼作為群狼的首領，其主要職責是發號指令，無需參與游走和圍攻過程。

（2）游走行為。游走行為的主要參與者是探狼，假設群狼中具有的探狼數量為Smum，當探狼向前進一步時，會把此時的目標函數值記錄下來，同時與之前的目標函數值進行對比分析，然后探狼選擇目標函數值大的方向前進，根據其前進情況實時更新探狼位置。探狼向第j(j=1,2,...,h)個方向前進后，探狼i在第d維的位置為：

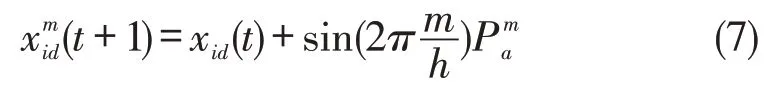
式（7）中，m取值范圍為{1,2,...,h}；Pa表示游走步長；a表示探狼的比例因子。

記探狼i在方向j處的目標函數值為Yij，計算獲得一次游走行為結束后最大的目標函數值所對應的探狼Ymax，接著與頭狼Ytoulang比較，若Ytoulang＜Ymax，則Ytoulang=Ymax，此時探狼Ytoulang將成為群狼的新頭狼，同時會對群狼發出召喚行為，若Ytoulang＞Ymax，則繼續實行游走行為，一直到探狼i的目標函數值Ytoulang＜Yi或達到最大游走次數。

（3）召喚行為。召喚行為的主要參與者為猛狼，首先頭狼向群狼發出召喚指令，頭狼附近區域的猛狼以步長Pb快速向頭狼所在位置靠近。假設頭狼附近區域擁有的猛狼數量為Mmum，且有Mmum=N-Smum，則會有：

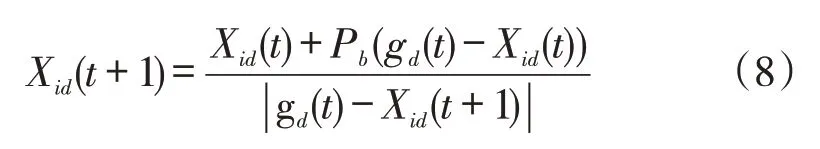
式（8）中，gd為第t代頭狼的位置，若猛狼的目標函數值大于頭狼，此時其將會被選取成為頭狼，并由該狼繼續召喚行為。如果一直未出現大于頭狼的目標函數值，則在猛狼前進至與頭狼的位置小于dnear時，停止召喚行為。其中dnear可以采用式（9）進行計算：

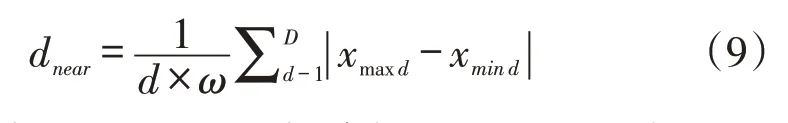
式（9）中，Xmaxd,Xmind分別表示d維空間內猛狼與頭狼之間的最大距離與最小距離；ω為距離判定因子。

（4）圍攻行為。頭狼具有最優目標函數值，為了成為頭狼，猛狼會對頭狼發出圍攻行為，假設猛狼圍攻步長為PC，則猛狼的圍攻行為見式（10）。

式（10）中，λ是[-1,1]范圍內的任一數值，在圍攻行為進行過程中，如果出現某猛狼的目標函數值大于頭狼，則該猛狼將取代原頭狼，成為新的頭狼，如果一直未出現狼當前位置的目標函數值大于原位置的情況，則狼位置一直保持不變。

此外，三種不同狼的圍攻步長之間的關系為：

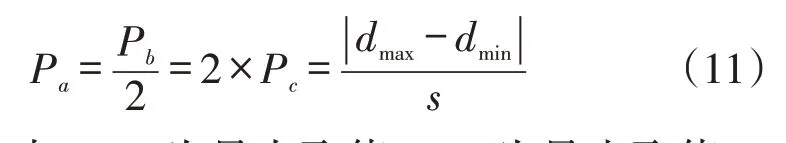
式（11）中，dmax為最大取值，dmin為最小取值，S為步長因子。

（5）更新群狼。根據“優勝劣汰適者生存”的原則，淘汰目標函數值最小的R匹狼，同時R是[N/2×ξ,N/2]中的任意數值，而ξ為群狼更新比例因子。

2.2 算法的優化改進

上述傳統的群狼算法中，群狼在進行游走行為的過程中，計算結果的精度受到h取值的限制，如果h值太小，則最終的計算結果只能是局部最優值，而非全局最優值；雖然h取值越大，最終計算的精度會越高，但是計算過程中的收斂速度會越來越慢，增加計算的復雜性。

為了解決游走行為過程中h取值的限制，提升計算精度，本文采用分數階對群狼算法進行改進，分數階導數結果雖然受到之前狀態的影響，但是隨著時間的推移，分數階導數結果會越來越小，同時具有極易固定的特點，非常適用于群狼游走行為這種不可逆問題的求解。綜上所述，本文將分數階應用于群狼算法優化后，游走行為可以描述為：

2.3 改進算法的求解過程

用上述改進的群狼算法求解建立的物流配送中心選址模型，將由配送中心組成的配送網絡看成群狼，配送中心則為狼，備選地址為搜索的空間維數，而需選擇的配送中心則為頭狼，具體步驟如下：

step1：頭狼選取。根據式（7）計算得到每一匹狼所在的位置，把目標函數值最大的狼作為頭狼。

step2：設置一個標準的適應度目標函數值，假如人工狼對氣味的感知濃度ω與適應度函數值相差較小，說明人工狼感知氣味濃度較小，反之，說明感知氣味濃度較大，將記錄為游走起點。

step3：頭狼向猛狼發出嚎叫，猛狼聽到召喚指令后，根據式（9）和式（11）向頭狼方向對附近區域進行搜索，不斷地靠近頭狼。

step4：頭狼通過嚎叫向群狼發出通知，群狼會根據式（10）和式（12）對頭狼發起圍攻。

step5：為了更好地適應自然的生存法則，根據式（7）對群狼進行淘汰選擇，最終只有m匹狼保存下來。

step6：不停重復上述操作，直至終止條件運行得到滿足，整個流程結束，得到計算結果和物流配送中心的最佳模擬選址情況。

3 仿真分析

3.1 仿真數據來源

為了對上述設計模型的科學性進行驗證，選取我國30個城市，從這些城市中選取6個物流配送中心。選取的30個城市坐標（x，y）和需求量（Wi）見表1。本文仿真采用的物流配送中心選址算法為改進群狼算法，同時為了分析改進后群狼算法的求解效果，將其與PSO算法和傳統群狼算法進行了對比分析。

表1 選取城市坐標及需求量

3.2 仿真分析

將本文優化改進的群狼算法應用至式（1）的物流配送中心選址模型中，尋優曲線如圖1(b)所示，根據尋優曲線，可得到改進群狼算法計算得到的目標函數最優解為5.478 0×105，仿真得到的最終選址方案結果如圖1(a)所示，由此可以看出，群狼算法計算獲得的6個配送中心所在城市分別為12，27，6，25，18，9。

圖1 改進群狼物流配送中心選址方案

3.3 不同算法對比分析

為了分析改進群狼算法的效果，采用粒子群算法（PSO）、傳統群狼算法（BWPA）對物流配送中心選址模型進行求解，同時對三種不同算法的求解結果進行對比分析。

由圖2(b)仿真計算的尋優曲線結果可知，采用粒子群算法獲得的目標函數最優解為5.727 0×105，同時由圖2(a)的選址方案結果可知，粒子群算法計算出的6個配送中心所在城市分別為29，28，5，20，3，9。

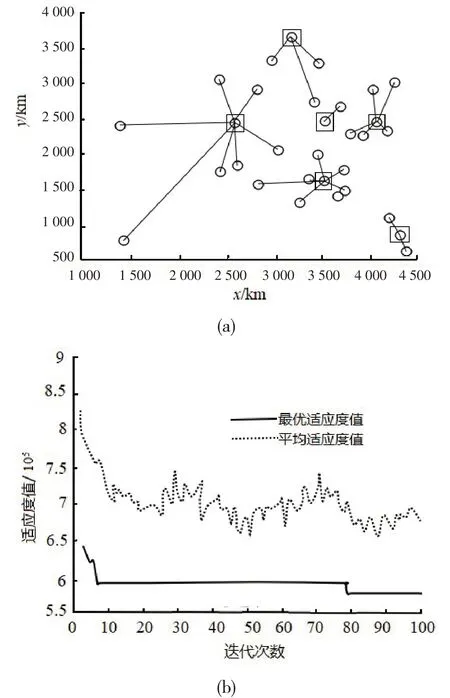
圖2 粒子群算法物流配送中心選址方案

傳統群狼算法仿真計算得到的尋優曲線如圖3(b)所示，得到的目標函數最優解為5.840 9×105，同時由圖3(a)的物流配送中心選址方案結果可知，獲得的6個配送中心所在城市分別為12，28，5，20，3，9。

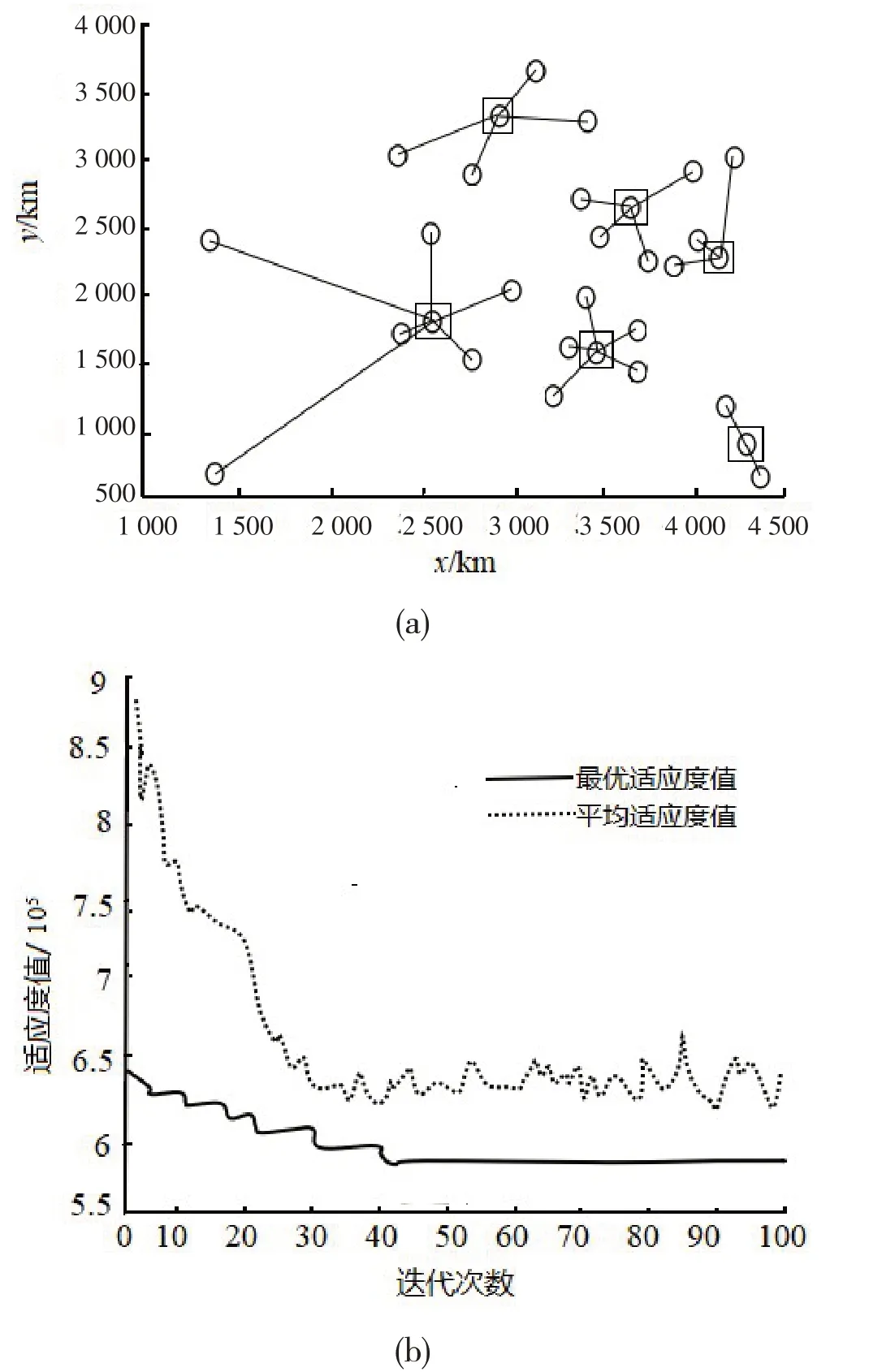
圖3 傳統群狼算法物流配送中心選址方案

為了比較分析以上三種算法的優劣勢，采用改進群狼算法、PSO算法和傳統群狼算法進行30次求解，其最優值、最差值、平均值和方差結果見表2。

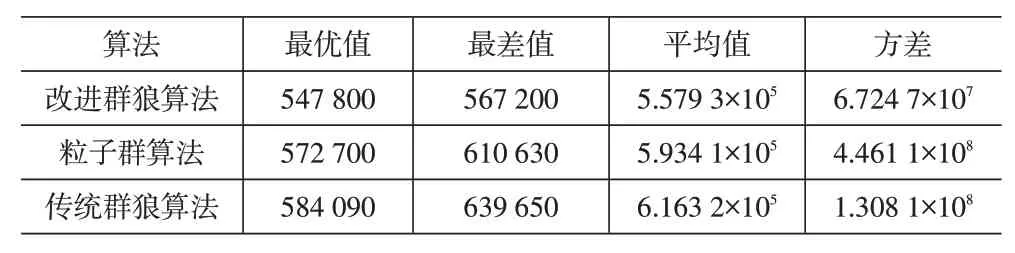
表2 3種不同算法獲得的計算結果

根據表2計算結果可以看出，本文設計的改進群狼算法方差最小，表明改進群狼算法求解得到的結果浮動性最低，最為穩定，可以很好地應用到物流配送中心選址中。

4 結語

近年來，我國物流行業業務量增長迅速，相應的物流配送中心數量也不斷增加，而物流配送中心的選址需要充分考慮客戶需求、物流效率、運輸成本和服務范圍等方面。因此，物流配送中心選址的合理性至關重要。目前配送中心選址的算法種類較多，但是都存在一定的局限性，群狼算法在物流配送中心選址方面得到了較為廣泛的應用，但是該算法在全局求解方面存在較大局限性。本文在傳統的群狼算法基礎上進行改進，且對改進的群狼算法的效果進行了對比分析，結果顯示，改進的群狼算法求解結果穩定性好，在物流配送中心的選址方面具有很好的應用效果。