生活性·直觀性·獨創性：構建自主探究的小學數學課堂

王麗慧

（詔安縣第一實驗小學，福建 漳州 363500）

學生是數學學習和發展的主體，在教學中，教師應以《義務教育數學課程標準（2011 年版）》理念為指導，“創造性地理解和使用教材”［1］，積極創新思路，改進教學策略，營造有利于學生自主、合作和探究學習的課堂氛圍，做到“從兒童視角出發，關注兒童的思維特點、心理特征、認知水平、思考習慣、知識經驗等富有兒童特性的數學思考”。［2］讓學生在掌握數學知識的過程中，激發數學情感，發展思維能力，培育創新精神。

一、生活性：激發數學情感

數學情感是指學生在學習數學的過程中，真切感受數學與生活的廣泛聯系，形成學習有意義的數學的積極心理情緒。數學知識由于其高度概括性與抽象性的特點，學生常常感到枯燥乏味，容易產生厭學情緒。教師要采用生活化的教學策略，激發學生的數學情感，使他們熱情地投入學習中。《數學課程標準解讀》指出：“學生學習數學，是學生生活常識的系統化，離不開學生現實的生活經驗。”在教學中，要采用生活化情境呈現的方法，營造生動、有趣的問題情境，使數學問題生活化，引領學生從數學的角度觀察、思考和解決問題，認識到“數學就在生活中”，感受學習“有用的數學”的樂趣，興致勃勃地參與問題探究。例如，教學有關“折扣”的知識，課前讓學生收集生活中有關“打折”的資料，課堂上出示以下問題：

學校響應“新冠肺炎疫情”防控號召，要買25 瓶洗手液。恒盛、萬利、旺城三家超市同時銷售一個品牌的洗手液，該品牌原價每瓶為16 元，恒盛超市打“八五”折，萬利超市“滿300 元打七五折”，旺城超市“買四送一”。請問學校到哪家商店購買最省錢？

學生經過討論，得出以下幾種購買方案：

（1）到恒盛超市購買：16×25×85%=340（元）

（2）到萬利超市購買：16×25=400（元），400×75%=300（元）

（3）到旺城超市購買：25÷（4＋1）=5，5×4×16=320（元）

教師啟發：哪個方案最為省錢？學生比較后得出：340 元〉320 元〉300 元，所以到萬利超市購買最省錢。學生知道哪家超市的“打折”方案更優惠，深入掌握“打折”的數學知識，形成實際數學應用的能力，數學情感得到培養。

二、直觀性：優化思維過程

數學學習中的思維過程，指的是學生運用數學知識、原理對問題進行分析、判斷，進而有效解決問題的思維活動。優化的思維過程體現數學學習的有效和高效。在教學中，教師積極創設直觀化問題情境，“是實施合作學習、自主探究、小組互動的前提條件”。［3］與以往的課本相比，現行數學教材添加了許多數學問題主題插圖，化抽象的數量關系、文字信息為直觀可感的形象，有利于拓寬思路、活躍思維。小學數學教材編排，其目的在于通過色彩豐富的主題插圖，吸引學生的注意力，并使其透過主題插圖展示的生活小情景，喚起生活經驗，感悟數學基本概念、數量關系及其計算方法，使數學學習思維過程簡單化。因此，應該充分發揮主題插圖的直觀作用，活躍互動氛圍，力求簡化、優化思維過程，提高學習質量與效率。例如，四年級下冊《旅游中的數學》，插圖展示以下問題：

四年級師生共32 名去公園劃船游玩，請你根據下面的說明，設計一種最省錢的租船方案。大船限乘6 人，租金30 元；小船限乘4 人，租金24 元。

讓學生題、圖結合，先算單人價格，尋找便宜的租船方案。直觀、形象的主題圖，直接喚起生活記憶，結合題目中的描述，學生提出：

生1：大船人均5 元，小船人均6 元，租大船比較便宜。

生2：全部租坐大船，有空位，會形成浪費。要看具體人數，才能判斷如何租船更便宜。

顯然，學生已經能夠借助主題圖進行細致思考。教師指導列表（表1），比較、確定最優方案：

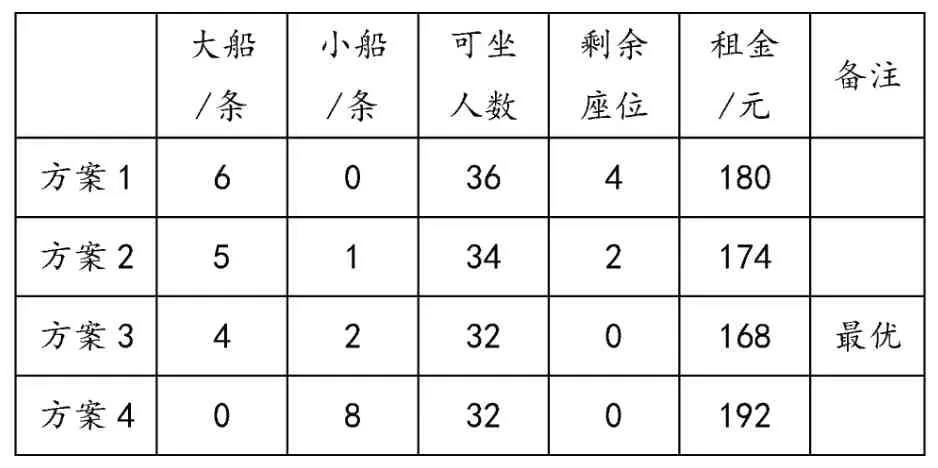
表1

通過主動交流、討論，學生經歷簡潔、明了的思維過程，獲得啟示：解決這類問題，不僅要考慮哪一種船便宜，還要考慮盡可能地使座位都坐滿。運用直觀的主題圖，化抽象的數量關系為具體可感的形象，學生通過觀察、分析、轉換解決問題，思維的靈活性得到培養。

三、獨創性：培育創新精神

數學創新精神是指學生懂得并且善于綜合運用數學知識、技能與方法，探索富有創意的問題解決思路的心理智慧品質。培養學生的創新精神，是新課程改革重要目標之一。在教學中，教師是學習的組織者、引導者與合作者，引導、鼓勵學生大膽嘗試，敢于探究，善于質疑，表達自己獨特的感悟。例如，教學六年下冊《圓柱的體積》，設計以下環節：1.將圓柱體教具沿底面直徑切分成32 等份。

2.將兩個半圓柱教具分別對拼成一個近似的長方體。

3.觀察割拼過程，想象：分得份數越來越多，直到足夠多份時，所拼成的立體圖形最終可以得到一個長方體。

4.比較得出：圓柱體的體積=底面積×高=圓周率×半徑的平方×高。

學生通過認真觀察、積極思考，進而發現規律，提高解題能力，培養創新精神。

教師再設計以下一道題：

一個圓柱形糧囤，從里面測，它的側面積是12.56平方米，底面直徑是4 米，這個圓柱形糧囤的容積是多少平方米？

學生按常規方法解答如下：

（1）高：12.56÷（3.14×4）=1（米）

（2）體積：4÷2=2（米）

3.14×2×2×1=12.56（立方米）

答：這個圓柱形糧囤的容積是12.56 平方米。

教師啟發：“有沒有更加簡便、高效的方法？”接著，演示圓柱體的體積公式推導過程，把拼成的長方體“放倒”、展開（如圖1）：

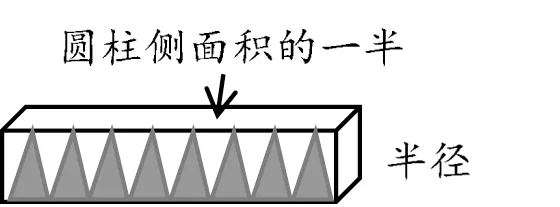
圖1

學生得出結論：這個長方體的底面積相當于圓柱體側面積的一半，高相當于圓柱體的半徑。于是，解題思路有所突破：

12.56÷2×（4÷2）=12.56（立方分米）

答：這個圓柱形糧囤的容積是12.56 平方米。

經過比對，學生在問題解決中，靈活調動所學知識來分析題目，創新解題思路，尋求最佳的解題方法。