關注方程思想，重視建模應用

唐倩

【摘要】數學方程是小學數學教學中的重點內容，筆者在實際教學中發現，運用方程解決實際問題對學生來說有些困難.本文追本溯源，幫助學生逐步建立方程的模型，繼而強化學生運用方程的意識，體會方程解決實際問題的優勢，旨在幫助學生掌握用方程解決實際問題的能力，從而提高學生的解題能力.

【關鍵詞】方程;方程思想;方程模型;方程意識

“簡易方程”安排在蘇教版五年級下冊第一單元，方程作為在一種新的思想方法，是學生從算術思維到代數思維的一種過渡，學生需要打破已有多年的算術思維的模式，運用方程來解決實際問題，對學生數學素養的提高有著重大的意義.在實際教學過程中，在等式的基礎上引入方程的概念，學生都能夠脫口而出：“含有未知數的等式是方程.”學生也能利用等式的性質解決一些簡易方程，但是在實際解決問題過程中，學生往往不會靈活選擇方程來解決實際問題.

一、關注方法——方程思想的拾起

簡易方程這一單元在解決實際問題過程中，出現了這樣一類題，要求選擇合適的方法解決下面的問題.

1.少先隊員參加植樹活動，五年級去了205人，四年級去的人數是五年級的1.2倍少12人，五年級去的人數比六年級的1.5倍少5人.

（1）四年級去了多少人？

（2）六年級去了多少人？

這道題的設計意圖很明顯，第一個問題利用算術方法方便解決，第二個問題利用方程更容易解決，但是在學生呈現的作業答案，兩種方法使用非常隨意，甚至出現方法對調的現象，讓我困惑不解.

在一次測試中，我特意關注了這樣的現象，解決實際問題中有這樣一道題：李老師和張老師每天早晨都在學校操場的環形跑道上跑步，跑道的全長是360米.如果李老師平均每秒跑6.5米，張老師平均每秒跑4.5米，而且他們從跑道的同一地點同時出發，都按逆時針方向跑，經過多長時間李老師正好比張老師多跑一圈？

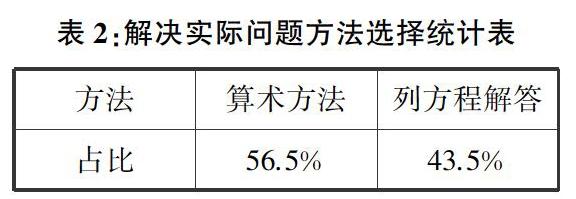
看完題目后，相信老師心中已經有了判斷，這是一道列方程解決相遇問題的典型習題，可是學生的正確率以及方法的選擇讓我很驚訝.我統計了我校五年級四個班161名學生的解答情況，結果如下.

結果顯示，不同班級正確率稍有差異，但是從整體上看這道解決實際問題的正確率較為均衡，都不算高.方法選擇上，十分明顯的是選擇算術方法的多于選擇方程方法的.學生為什么會選擇算術方法而不選擇方程解答呢？我十分疑惑.課后隨機詢問了年級中的幾名同學，他們幾乎一致地告訴我，方程的解答過程太煩瑣了，需要寫“解”“設”，解方程也比較麻煩.還有一部分學生表示，當時沒有想到解方程這種方法，就用算術方法做，結果做錯了.

看來，想要讓學生學會列方程解決實際問題，就要從根源抓起，讓學生真正理解方程的內涵，讓學生心中有方程，甚至喜歡上方程.

二、追本溯源——方程模型的建立

在學習方程之前，學生從來沒有接觸過方程，雖然之前教師沒有提出方程的概念，但是學生實際上已經有了方程的意識.那么，方程到底從何而來呢？

（一）四則運算中滲透方程意識

一年級開始就有類似的題：（ ）+3=10，要填出括號里的數，實質上就是在求未知數.記得當時教學時會讓學生思考，幾加3等于10呢，這就是方程的觀念.看來從一年級開始就有方程意識的滲透！之后的運算中像這樣的練習更多了，比如△×△×△=8，△+□=11，△=（ ?），□=（ ?）.在這樣一次次練習中，“方程”已悄然在孩子心中播下了一顆種子.

（二）用字母表示數鋪墊方程概念

五年級上學期學習用字母表示數，這是一個獨立單元，教師往往就教材而教，忽略了這部分內容與前后的聯系，這一單元實際就是為了學習方程作鋪墊的，讓學生學會用含有字母的式子表示數以及數量關系，正確厘清數量之間的關系，并學會用含有未知數的表達式列方程解決實際問題.

（三）簡易方程構建方程模型

《數學課程標準》指出：“模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑.” 我覺得方程是建立未知與已知之間等量關系的模型.在這一單元教學過程中要循序漸進，讓學生有效地參與學習和探索活動，讓學生在自主探索和合作交流中逐步理解方程的含義和解法，經歷列方程解決實際問題的過程，不斷體會方程的特點和實際應用價值.在初步認識方程中，教師可利用天平這一工具進行演示，讓學生能夠直觀地感受到數量之間的等量關系，體會方程的特點及含義，也是直觀建立方程模型的過程.

對學生來說，從具體的、確定的數過渡到用字母表示未知的、可變的數，再由列算式解決實際問題到列方程解決實際問題，這是認識上的一次飛躍，更是思維的一個大轉折.在概念學習的過程中教師提前向學生滲透方程建模的意識與方法，把握方程模型最核心的價值，有利于幫助學生突破列方程解決實際問題的難點.

三、指導過程——方程應用意識的植入

（一）提高學生解方程的能力

部分學生不愿意用列方程解決實際問題，就是因為他們解方程能力薄弱.在列方程解決實際問題過程中，有的只需要一步計算，而有的需要兩步或者三步計算.在教學解方程的過程中，教師通常要求學生利用等式的性質來解方程，學生也初步掌握了x+a=b，x-a=b，ax=b和x÷a=b等一步計算方程的解法.對于一些特別的方程，例如a-x=b，a-bx=c，教師需要啟發他們靈活運用已有經驗以及等式的性質去解決，進一步理解方程的特點及解法，提高解方程的能力.

（二）突出方程方法的優勢

在學生由算數方法向方程方法過渡時，教師在注重方程格式的同時，要突出運用方程解決實際問題的優越性.教師可以設計同樣一道題目，用算數方法解起來很煩瑣，而用方程解起來卻輕而易舉，讓學生對數學方程的學習產生興趣.

例如，學生錯誤率極高的這道練習：少先隊員參加植樹活動，五年級去了205人，四年級去的人數是五年級的1.2倍少12人，五年級去的人數比六年級的1.5倍少5人.

（1）四年級去了多少人？

（2）六年級去了多少人？

教師要引導學生找出題中的數量關系，四年級的人數等于五年級人數×1.2-12，由于五年級人數是已知的，因此直接列算式非常方便.六年級人數的數量關系是五年級人數=六年級人數×1.5-5.數量關系中已知的是五年級人數，六年級人數是未知的，為了順應思維順序，可以設六年級人數為x，這樣自然而然地就可以列方程解決了.

我們還可以通過兩種方法的對比，進一步讓學生體會方程的優勢.求六年級的人數的關系式是：五年級人數=六年級人數×1.5-5.運用方程解決是順向思維，如果一定要運用算術方法解決，那我們就要逆向思維了，難度一下子提升了.條件“五年級去的人數比六年級的1.5倍少5人”，已經知道的是五年級的人數，那我們可以先算出六年級人數的1.5倍，也就是五年級的人數多5人，列式為205+5=210（人），也就是210人是六年級的1.5倍，六年級的人數為210÷1.5=140（人）.相信通過這樣的對比練習，學生能夠領悟到算術方法和方程之間的聯系與區別，更能凸顯出方程在這一類題型中的優勢所在，也有利于以后解題方法的選擇.

（三）依靠常見數量關系列方程

列方程解決實際問題最關鍵的就是厘清條件與問題之間的數量關系，按照順向思維順序，利用未知數，列出方程，并且解方程.因此把握數量關系是列方程解決問題的前提條件.題目千千萬萬，有一些最基本的數量關系是不變的，比如：涉及行程問題時，要能想到：速度×時間=路程，涉及購物問題時，要能想到：單價×數量=總價，還要想到數量之間的比較，數量之間的倍數關系等.其他一些較為復雜的數量關系實際上就是由這些基本的數量關系組合而成的.依靠常見的數量關系，能夠幫助我們逐步探究出正確的等量關系，從而依據等量關系，列出正確的方程.

為了進一步突破找準數量關系這一難點，教師可以設計找等量關系的專項練習，幫助學生學會根據不同的具體情境發現其中的等量關系并列出方程，學會判斷哪些等量關系能列出方程.

（四）練習中培養學生用方程解決問題的意識

為了鞏固列方程解決實際問題這一新本領，強化學生運用方程模型的意識，教師在教學后安排適量的練習是非常有必要的.教師還要有針對性地設計一些稍復雜的問題，讓學生在解決問題的過程中，體會方程的優越性，培養他們用方程解決問題的意識.

例如，在列方程解決問題練習中，可以設計這樣的題目：某市實行階梯水價，規定每戶每月用水量在標準量以內部分的水價為3元/ 噸，超過的部分水價為5元/噸，李阿姨家上個月用水 13噸，交水費 49 元.該市每戶每月用水的標準是多少噸？

解決問題先找數量關系，規定部分的水費+超過部分的水費=49元.這樣的問題用算術方法解決比較復雜，而用方程解答則思路很順暢，很容易理解等量關系，求出正確的結果.當然在解決問題過程中教師不需要每題都明確用方程解決，先讓學生嘗試自己解決，在解決中發現有困難可以適當點撥，解決后也可以對比算算術方法和方程，不能光比形式上，更重要的是讓學生說說思維的過程.在這樣自己解答，對比方法的過程中，學生能夠清晰地感知到用方程解決問題的優勢，并自覺地構建方程思想.

以上是筆者在教學用方程解決實際問題過程中的一些發現與思考.我知道方程教學也只是代數領域的一個墊腳石，能為今后學習更復雜的數學問題奠定基礎.因此，在方程教學中，我們要引導學生感受方程思想，體會用方程解決問題的優越性，打破學生固有思維，滲透代數思想，提高學生解決實際問題的能力.

【參考文獻】

[1]韓谷海.淺談小學數學方程教學的有效性[J].內蒙古教育（職教版），2015（10）：86-87.

[2]孫政.小學數學教學中滲透方程思想的策略探微[J].教育觀察（中下旬刊），2015（12）：109-110.

[3]陸嫻靜.小學生方程學習中的常見困惑與教學對策.小學數學教育2017（Z2）：9-10.