迭代運算使不連續映射變為光滑映射
劉曉華,羅天琦
1.樂山師范學院 數理學院,四川 樂山 614000;2.樂山師范學院 教師教育學院,四川 樂山 614000

迭代運算是數學中的重要運算之一,它在許多復雜的問題,如分岔、混沌和分形[1-3]問題、多項式[4-8]、擬多項式[9-10]、線性分式[11]和有理函數[12]等問題中有廣泛的應用.在一維的情況下,高次迭代的計算也是一項復雜的工作.隨著C0映射迭代理論的發展[13-14],人們也逐漸開始研究不連續映射或者集值映射等“壞映射”的迭代和它們的迭代根[15-18].
通常,人們認為一個“壞映射”可能會通過迭代運算變得更加復雜,但文獻[19]表明不連續的自映射通過迭代運算可能變為連續的自映射,并給出了在緊區間上只有一個間斷點的分段C0自映射的二次迭代連續性的充要條件.文獻[20]進一步研究了在緊區間上只有一個非光滑點的連續自映射二次迭代的光滑性,并給出了它們的二次迭代是C1光滑映射的充要條件.文獻[20]的工作不是對文獻[19]的工作的重復,因為文獻[20]所考慮的映射的導數可能不是自映射.綜合文獻[19-20],我們可以判斷在緊區間上只有一個間斷點的分段C1自映射四次迭代的C1光滑性.但是我們還不能判斷:在緊區間上什么不連續的自映射的二次迭代不僅連續而且C1光滑? 例如,自映射
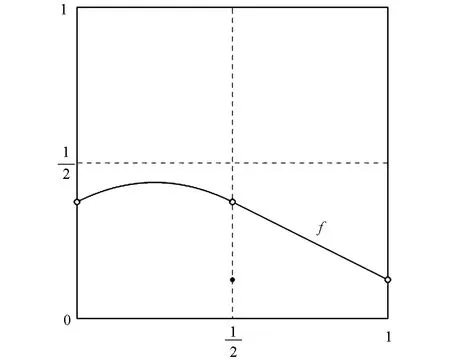
圖1 f有一個可去間斷點
在(0,1)上是C1光滑的(圖2).

圖2 f2在(0,1)上是C1光滑的
本文研究在區間I=(0,1)上只有一個可去間斷點的所有分段C1自映射Vr(I,I).每個f∈Vr(I,I)能被表示為
(1)
其中,x0∈(0,1)是f唯一的可去間斷點,f1和f2分別在I1和I2上是C1光滑的,c∈(0,1)是一個常數.為了研究在Vr(I,I)中映射的二次迭代的光滑性,我們需要將Vr(I,I)分成一些子類,即Vr(I,I)=Vrr(I,I)∪Vrj(I,I)∪Vro(I,I)∪Vr∞(I,I),其中:


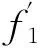
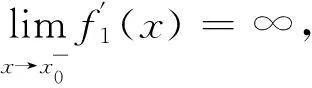
本文討論Vr(I,I)中映射的二次迭代的C1光滑性.首先給出了在Vrτ(I,I)中映射的二次迭代是C1光滑映射的充要條件,其中τ∈{r,j,o},獲得了在Vr∞(I,I)中映射的二次迭代是C1光滑映射的必要條件.其次說明了找Vr∞(I,I)中映射的二次迭代是C1光滑映射的充分條件的困難.最后用例子展示了在Vr(I,I)中映射的二次迭代是C1光滑映射的條件.
下面討論由(1)式定義的f∈Vr(I,I)的二次迭代的光滑性.記
(2)
為了方便,記
Crr(I,I)={f∈Vrr(I,I)|f(y0)=Γ(c)}
Crτ(I,I)={f∈Vrτ(I,I)|f(y0)=Γ(c)和f′(y0)=0}τ∈{j,o,∞}
我們用D+f和D-f分別表示f的右導數和f的左導數.
定理1假定f∈Vrτ(I,I)由(1)式定義,其中τ∈{r,j,o},且f有唯一的間斷點x0∈(0,1).令y0由(2)式定義.那么,f2在I上是C1光滑的當且僅當y0∈Ii,f(I1∪I2)?Ii成立(i=1,2)和f∈Crτ(I,I).
證首先證明必要性.假定f2在I上是C1光滑的,那么f2在I上是連續的.由文獻[19]的定理1知,y0∈Ii,f(I1∪I2)?Ii和
f(y0)=fi(y0)=Γ(c)
(3)
其中i=1,2.在下文中,我們只討論y0∈I1和f(I1∪I2)?I1的情況,因為y0∈I2和f(I1∪I2)?I2情況的討論與y0∈I1和f(I1∪I2)?I1情況的討論是完全類似的.下證在y0∈I1和f(I1∪I2)?I1的情況下,有
(4)
假設f∈Vrτ(I,I),其中τ∈{r,j,o}.
情形1f∈Vrr(I,I).由(3)式和Crr(I,I)的定義,我們知道f∈Crr(I,I).
情形2f∈Vrj(I,I).由Vrj(I,I)的定義,我們有
由(4)式得到f2在x0的左導數和右導數分別為
(5)
(6)
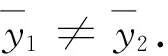
(7)
由(3),(7)式和Crj(I,I)的定義,我們知道f∈Crj(I,I).
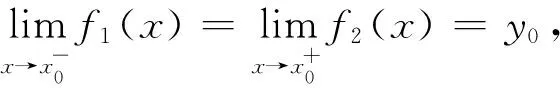
(8)
(9)
注意到
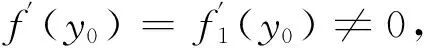

其次證明充分性.我們僅證明y0∈I1,f(I1∪I2)?I1的情況.
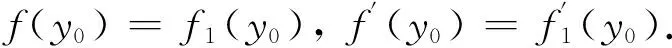
當f∈Crr(I,I)時,由Crr(I,I)的定義有f(y0)=f1(y0)=Γ(c)和f∈Vrr(I,I).由文獻[19]的定理1知f2在I上是連續的.因為f∈Vrr(I,I),則
由(4)式能獲得(5)式和(6)式,則D-f2(x0)=D+f2(x0).因此,f2在I上是C1光滑的.
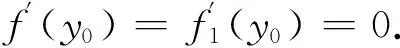

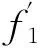
綜上所述,f2在I上是C1光滑的.
定理2假定f∈Vr∞(I,I)由(1)式定義,x0∈(0,1)是f的唯一間斷點.令y0由(2)式定義.假設f2在I上是C1光滑的,則y0∈Ii,f(I1∪I2)?Ii(i=1,2),且f∈Cr∞(I,I).
證證明方法與定理1中f∈Vro(I,I)的必要性的證明完全類似.


其中



圖3 F1有唯一可去間斷點
其中
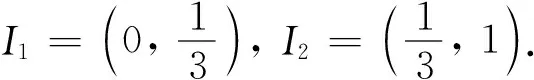
它在(0,1)上是C1光滑的(圖4).

圖在(0,1)上是C1光滑的


圖5 F2有唯一的可去間斷點
而且
則F2∈Vro(I,I).注意到

它在(0,1)上是C1光滑的(圖6).

圖在(0,1)上是C1光滑的


在這篇文章中,我們僅考慮了(1)式定義的映射唯一的間斷點是可去間斷點的情形,對(1)式定義的映射唯一間斷點是跳躍或者振蕩間斷點的情形,我們將在后續文章中加以研究.

