考慮漸進變形和潤滑劑的滾動軸承外圈單點故障動力學模型

李云龍，李志農，陶俊勇，許貝

(1.南昌航空大學,南昌 330063；2.無損檢測技術教育部重點實驗室，南昌 330063；3.廣西大學 機械工程學院，南寧 530004；4.國防科學技術大學裝備綜合保障技術重點實驗室，長沙 410073)

為提高滾動軸承的使用壽命并降低其振動噪聲，有必要對滾動軸承的動力學性能展開研究。目前，國內外研究者針對滾動軸承外圈單一缺陷建立了一些行之有效的動力學模型：文獻[1]用彈簧模擬軸承溝道與鋼球間的接觸關系，簡化了軸承的振動模型并建立了外圈損傷的簡化方程，大大降低了滾動軸承動態分析的復雜度；文獻[2]在考慮徑向游隙、幾何尺寸、故障脈沖等因素的前提下建立了滾動軸承外圈單一故障的振動模型；文獻[3]考慮接觸力和徑向游隙的影響，給出了軸承外圈局部缺陷的數學表達式，建立了滾動軸承故障的動力學模型；文獻[4]考慮了外圈損傷以及接觸載荷等因素的影響，建立了滾動軸承動力學微分方程；文獻[5]建立了考慮接觸變形量的外圈損傷模型，探究了故障尺寸對接觸變形量的影響；文獻[6]以滾動軸承系統的運動狀態為著重點，考慮外圈故障對赫茲接觸剛度的影響，建立了滾動軸承外圈剝離失效模型；文獻[7]引入缺陷尺寸建立了用于評估故障嚴重性的非線性振動模型；文獻[8]考慮油膜及滾動體滑動，改進了滾動軸承外圈單點故障的五自由度動力學模型并對不同故障參數對應的模型進行了分析；文獻[9]基于時變位移建立了滾動軸承復合故障的四自由度動力學模型，研究不同條件下滾動軸承的振動特性；文獻[10]將不平衡激勵引入外圈單一缺陷滾動軸承的動力學建模中，建立了不平衡影響下外圈單一缺陷滾動軸承的二自由度動力學模型；文獻[11]考慮了自由度及高速的作用，提出了一種用于外圈故障滾動軸承的五自由度動力模型；文獻[12]考慮滾動軸承外圈故障數量及間隔等因素對動力學特征的影響，建立了含外圈多點故障的滾動軸承五自由度模型。

雖然滾動軸承動力學建模取得一些進展，但幾乎所有文獻都認為滾動體與外圈故障一側邊緣剛接觸以及準備離開故障另一側邊緣時會立刻釋放和恢復所有的變形量。然而，該變形量的變化應是漸變的過程，且軸承在實際工況中處于潤滑狀態，即存在一定的油膜并產生黏性阻力。據此，本文以含外圈單點故障的滾動軸承為研究對象，在課題組研究的基礎上[13]，綜合考慮接觸變形量的逐漸變化過程和潤滑劑條件，建立考慮潤滑劑的滾動軸承漸進模型并與傳統的瞬變模型進行對比分析。

1 滾動軸承動力學模型的建立

假設滾動軸承外圈存在一處如圖1所示的故障，Φspall為故障的起始位置角，由于軸承外圈與機架多采用緊配合，Φspall保持不變。

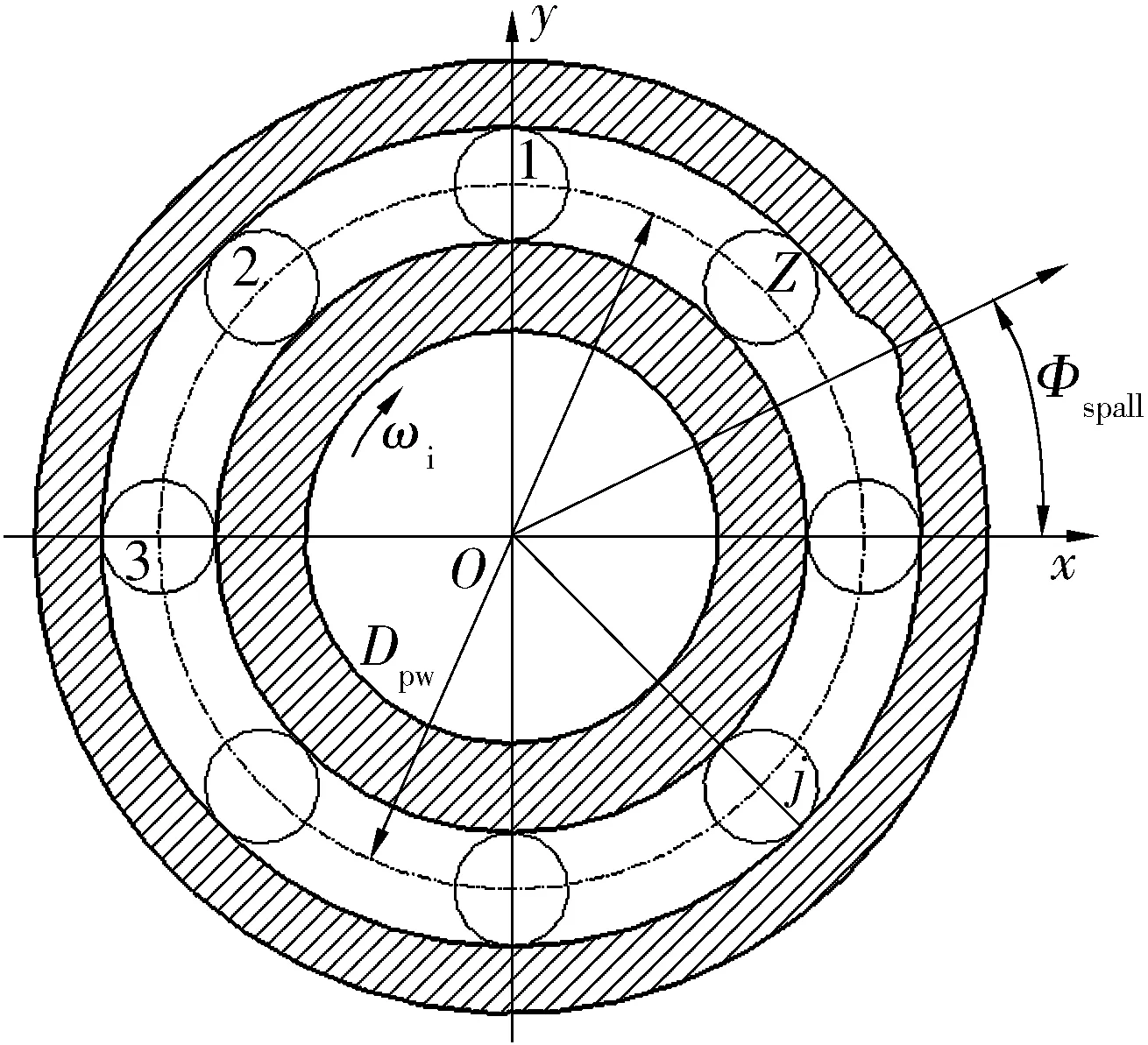
圖1 外圈單點故障的模型示意圖Fig.1 Model diagram of outer ring with single point fault

當第j個滾動體與軸承的內、外滾道發生接觸時，將產生一定的變形[14-15]，總變形量δj為

δj=xcosθj+ysinθj，

(1)

(2)

(3)

式中：θj為第j個滾動體中心的位置角；nc為保持架轉速；Z為滾動體個數；θ1為1#滾動體的起始位置角；α為接觸角；ni為轉子轉速；Dw為滾動體直徑；Dpw為滾子組節圓直徑。

單個滾動體經過外圈故障產生的變形量會周期性的釋放和恢復[16]，可表示為

δj=xcosθj+ysinθj-Gr-βjλ，

(4)

(5)

(6)

式中：Gr為徑向游隙；λ為滾動體經過故障區域時的瞬時變形量；βj為開關函數；φs為故障的跨度角；bc為故障寬度的一半；Ri為內圈內半徑。

目前，大多數外圈故障模型均采用理想化的矩形缺口，缺陷深度被定義為圖2b中的d′。漸進模型則假設缺陷截面為圓弧形，同時假設缺陷位于底部，且軸承載荷為豎直向下作用于內圈。滾動體通過該缺陷將產生彈性變形，變形的釋放和恢復是漸變的。只有滾動體接觸缺陷底部時，變形量才會等于缺陷高度。因此，漸變釋放的瞬時變形量為

圖2 滾動體與外圈單點故障的接觸Fig.2 Contact between rolling element and outer ring with single point fault

(7)

λmax=Cdr-Cde，

(8)

(9)

(10)

式中：λmax為最大變形量；Cdr為滾動體變形量；Cde為外圈變形量；Re為外圈外半徑。

滾動體與滾道之間為點接觸，則單個滾動體與滾道的接觸載荷為

(11)

K=1/[(1/Ke)2/3+(1/Ki)2/3]m，

(12)

式中：K為等效接觸變形系數，可以通過內、外圈的接觸變形系數計算得到[17]；Ki和Ke分別為滾動體與內、外圈滾道接觸的變形系數；m為引入的常數，取m=1.5。

由于滾動體與外圈之間存在潤滑油，滾動體旋轉時將產生油膜摩擦阻力[18]。軸承工況復雜多變，很難確定真實的摩擦阻力，大多數模型采用經驗或半經驗模型表示滾動體與滾道之間的油膜摩擦阻力[19-20]，本文則采用牛頓流體模型，即將潤滑劑考慮為牛頓流體，第j個滾動體受到的切向油膜摩擦阻力為[21]

τ=ηv/hj，

(13)

式中：η為實際工況下潤滑劑的動力黏度；v為滾動體相對外圈滾道的滑動速度；hj為彈流潤滑油膜厚度[22-23]。

潤滑劑的動力黏度與軸承實際工況下的壓力與溫度有關[24]，即

η=η0exp(σp)，

(14)

式中：η0為標準大氣壓下的空氣動力黏度；σ為黏度的壓力指數；p為接觸處的壓力[25]。

滾動體在自轉以及公轉的過程中，相對外圈容易發生滑動，其相對滑動速度為

(15)

γ=Dwcosα/(2Dpw)，

(16)

式中：nb為滾動體自轉速度；γ為系數。

將全部滾動體的接觸載荷投影在x，y軸這2個方向，得到的總接觸載荷為

(17)

滾動軸承通常承受徑向載荷的作用，軸向載荷不大[26]。根據牛頓第二定律和拉格朗日方程建立的滾動軸承外圈單點故障動力學方程為

(18)

式中：m為軸承質量；c為等效阻尼；Fr為施加在外圈表面的載荷；φ為Fr與x軸的夾角;g為重力加速度。

2 數值仿真

對SKF6205軸承進行仿真分析，軸承參數及仿真條件見表1，計算可得軸承轉頻fr為29.53 Hz，外圈故障特征頻率fe為105.87 Hz。

表1 軸承主要參數及仿真條件Tab.1 Main parameters and simulation conditions of bearing

用龍格-庫塔法對建立的滾動軸承動力學方程求解，得到滾動軸承的時域響應曲線。外圈單點故障軸承的瞬變模型與漸進模型的時域波形如圖3所示:當滾動軸承具有外圈單點故障時，瞬變模型和漸進模型的振動信號都呈周期性變化；位移曲線在0.1 s內約存在3個準三角周期函數信號，即頻率為30 Hz，對應于轉子轉頻29.53 Hz；位移、速度和加速度曲線在0.1 s內約有10～11次沖擊，故障頻率約100 ～110 Hz，對應于理論值105.87 Hz；瞬變模型振動信號的時域波形與漸進模型的變化趨勢基本一致，但漸進模型波形的幅值比瞬變模型的大，更能反映故障的信息。

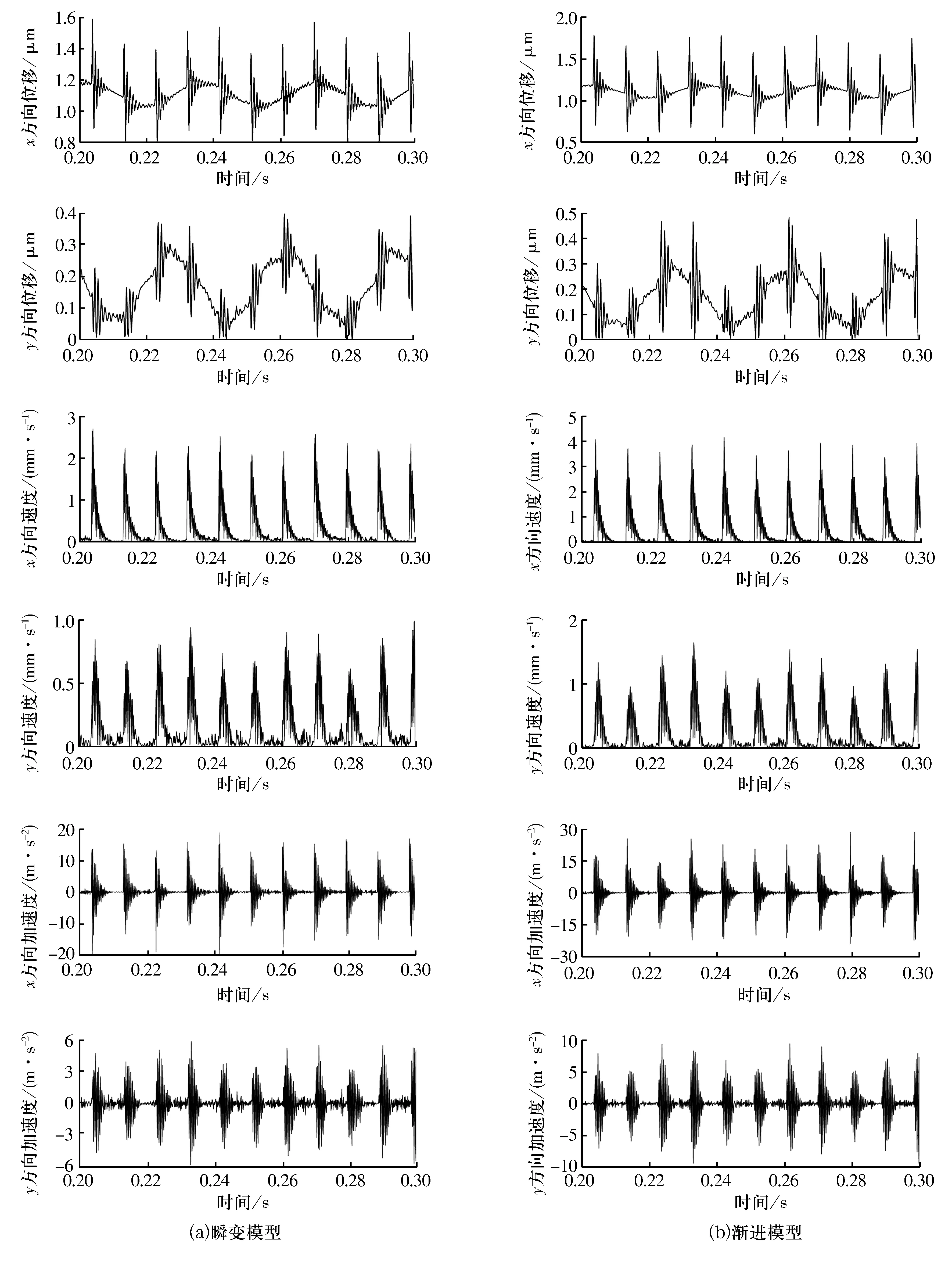
圖3 外圈單點故障軸承瞬變模型與漸進模型的時域波形Fig.3 Time domain waveforms of transient model and progressive model for bearing with single point fault in outer ring

對得到的信號進行傅里葉變換，得到滾動軸承外圈低頻段的頻譜如圖4所示：瞬變模型和漸進模型的頻譜都包括了轉頻(29.31 Hz)、外圈故障特征頻率及其高次諧波(105.0，212.5，317.5 Hz)，與理論結果一致，但漸進模型的頻率幅值更大，故障特征更為明顯。

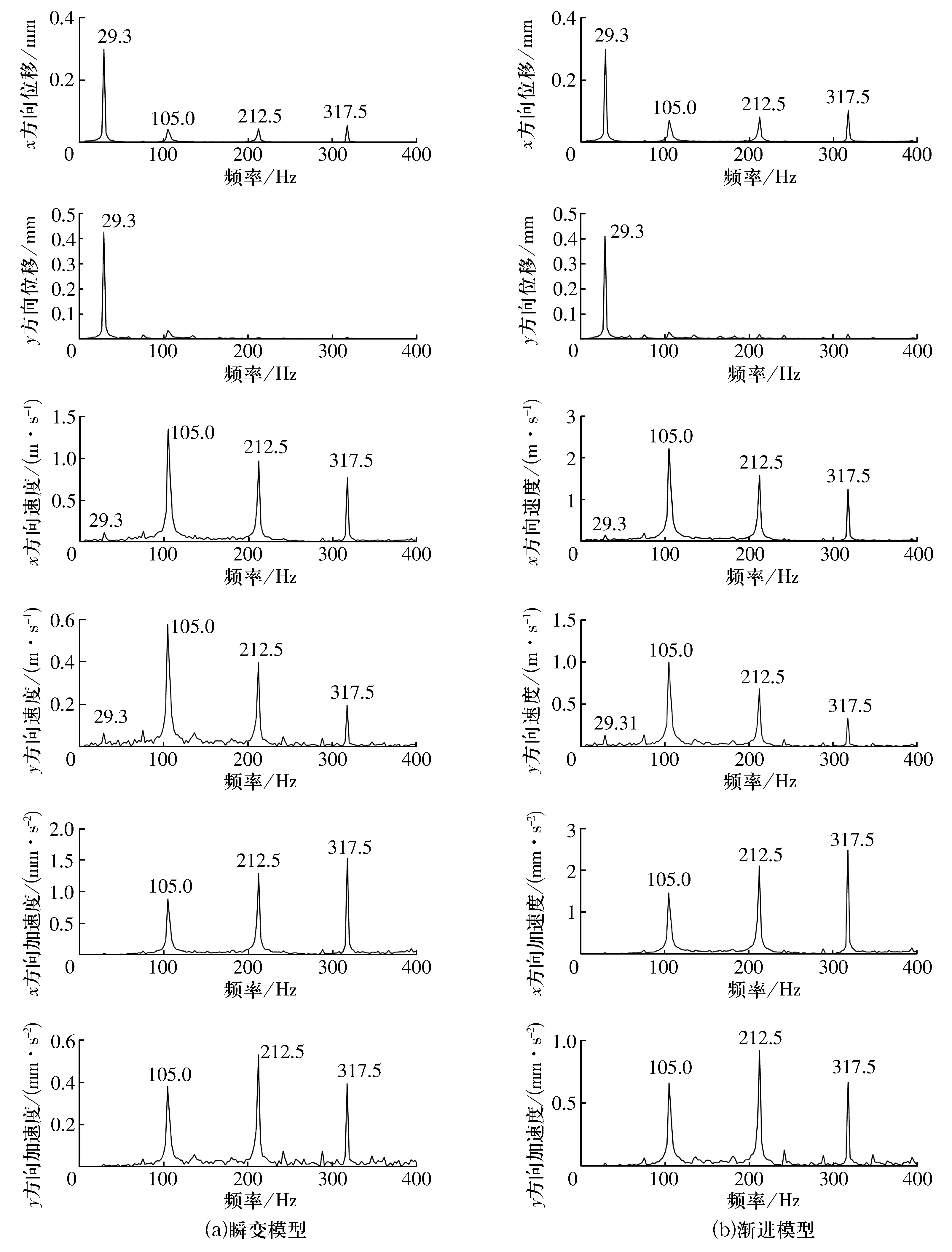
圖4 外圈單點故障軸承瞬變模型與漸進模型的低頻段頻譜Fig.4 Low frequency spectrums of transient model and progressive model for bearing with single point fault in outer ring

為進一步證明所建模型的正確性，分別在1 000，2 000，3 000，4 000和5 000 r/min轉速下進行仿真，結果見表2：不同轉速下的轉頻相對誤差均小于3%，故障特征頻率相對誤差則不大于0.5%，充分驗證了所建立模型的正確性。

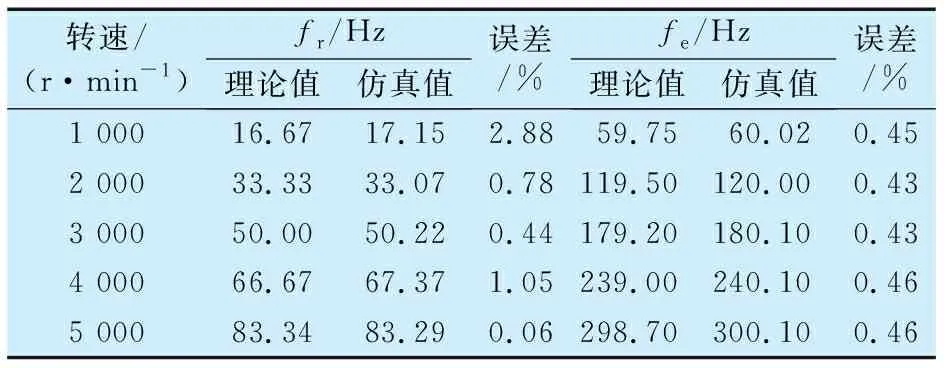
表2 不同轉速下軸承轉頻及故障特征頻率理論值和仿真值的對比Tab.2 Comparison between theoretical values and simulation values of bearing rotational frequency and fault characteristic frequency under different speeds

3 試驗研究

采用美國凱斯西儲大學標準試驗臺滾動軸承驅動端的數據[27]驗證仿真結果的有效性，該組數據采用SKF6205軸承，轉速為1 772 r/min，通過電火花在外圈溝道底部加工一個直徑0.178 mm的單點故障，其豎直方向的時域波形及低頻段頻譜如圖5所示，時域波形基本無法得出任何故障信息，頻譜圖中可以發現外圈故障特征頻率fe及其倍頻(105.8，212.0，318.2 Hz)，以及軸承運轉過程中背景噪聲引起的干擾頻率。

圖5 SKF6205軸承外圈單點蝕故障的試驗結果Fig.5 Test results of bearing SKF6205 with single point fault in outer ring

外圈單點故障的仿真結果與試驗結果的對比見表3，仿真結果與試驗結果均接近理論值，故障頻率的誤差在0.82%以下，進一步證實了所建立模型的正確性。

表3 本文模型的仿真結果與西儲大學軸承數據的對比Tab.3 Comparison between simulation results of this model and bearing data of Case Western Reserve University

4 結束語

本文建立了有潤滑劑條件下滾動軸承外圈含局部損傷故障的動力學模型，進一步揭示了外圈單點故障的機理。運用模型仿真得到了時域振動位移曲線、速度曲線以及對應的頻譜圖，分析發現外圈低頻信號的主要成分是轉子轉頻和滾動體通過故障特征頻率，新建立的漸進模型比瞬變模型更能反映故障的特征信息。通過不同轉速下的仿真結果以及試驗數據證明了本文模型的有效性，并證實了所提出的滾動軸承外圈單點故障模型是正確的。