基于最大覆蓋模型的救護車車輛調度問題研究
黃美林 馮 倩 王 雷 蔣 偉
(重慶交通大學 經濟與管理學院,重慶 400074)
1 問題描述與模型的建立
時間是衡量救護車出車效率的一個重要指標,現伊薩卡市要求將響應時間控制在6分鐘內,并計算出需要的救護車數量以實現此目標,除此之外救護車的位置需明確。若在伊薩卡市難以在6分鐘內到達的地區,可以增加最壞情況下的響應時間,以提高救護車的效用。
首先根據伊薩卡市地圖特點,將地圖建立3×3網格,分塊化處理并為其編號為N=1…9,將復雜的城市區域簡單化,利用救護車行駛模型對伊薩卡市現有的4個救護車站點進行驗證是否滿足6分鐘以內到達指定地區的限制條件。伊薩卡市已知有4個救護車站點,求出各救護車到呼叫點的行駛距離dij。救護車到達呼叫點的時間t應在6分鐘以內,將時間轉化為距離s,假設該救護車的時速v為55km/h(0.57miles/min)。每個呼叫點只需一輛救護車響應。根據以上約束以及目標函數為最短路建立模型:
2 車輛調度優化模型
首先根據伊薩卡市的地圖,對伊薩卡市進行模塊化,再根據救護車到達呼叫點的時間約束,利用最大覆蓋模型,尋找到最有數量的救護車站點數量以及位置。以最少的救護車站點去滿足所有呼叫需求點,所以目標函數為路徑最短。每個呼叫需求點i只有一輛救護車響應。每輛救護車的響應時間必須在6分鐘以內,其可轉化為行駛距離。
人們在遇到緊急情況首先會想到呼叫救護車急救,而影響呼叫量有很多因素,我們將老年人的呼叫量、突發疾病的呼叫量、經濟收入中等偏上人群的呼叫量、意外事故引起的呼叫量及護理機構引起的呼叫量作為影響因素。通過相關性分析,檢驗這些影響因素對呼叫量的相關程度,并對相關程度進行重要程度D計算,從而將影響因素定量化。
其中,D為影響因素的重要程度,dlevel為等級數,dtotal為總等級數。
將重要程度進行歸一化處理。根據伊薩卡市一年的呼叫數,計算平均每天的呼叫數。根據歸一化結果以及平均每天呼叫數計算各救護車站點里的救護車數量。由于每個救護車站點的救護車數量有限,若呼叫需求小于該站點救護車的數量,則該站點的車輛滿足調度。若呼叫需求過多,該站點的救護車全部出動,此時滿足不了需求,則需要考慮從其他站點調配救護車前往救援,但仍需要滿足在6分鐘內到達需求點。基于救護車行駛距離最短模型求解的站點,仍以救護車行駛距離最短為目標函數。所有站點的救護車行駛的距離均要滿足在6分鐘行駛的距離內。每個呼叫點僅有一輛救護車響應。根據以上約束建立車輛調度模型:
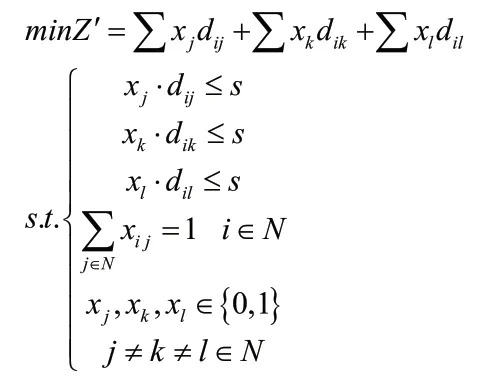
其中,minZ′=∑x j dij+∑x k dik+∑xl dil為目標函數,其表示救護車行駛距離最短,x j,x k,xl均為0-1變量;x j?d ij≤s,x k?dik≤s,xl?d il≤s表示所有站點的救護車行駛的距離均要滿足在6分鐘行駛的距離內;表示每個呼叫點僅有一輛救護車響應。
3 結果分析
利用MATLAB進行求解救護車行駛距離模型,所有約束滿足。此時,通過減少站點數量來尋找最優站點數量,減少成本。經過分析可以發現,一個站點是不可能在6分鐘以內到達所有可能的呼叫點,所以我們將站點減少至2和3,帶入模型求解。由于對角線為最長距離,分別對兩條對角線的距離進行計算,得到兩條對角線的距離為8.17英里和8.21英里,救護車需要在6分鐘內到達呼叫點,則該最大距離為3.42英里,因此在該城市內2個救護車急救站點不能滿足需求。當建立3各救護車站點時,每個救護車急救站點相鄰區域的距離均在3.42英里內,因此建設3個救護車急救站點滿足該城市6分鐘內響應。
運用貪婪算法求解最大覆蓋模型,求的結果為只需要在1、7、10區域設置3個救護車站點就能夠覆蓋伊薩卡市所有可能的需求呼叫點,根據影響因素計算各救護車站點的救護車數量為1區域5輛,7區域9輛,10區域6輛,利用遺傳算法求解車輛調度模型,根據計算結果可以得到,有一部分區域只有特定的一個站點能到達而另一部分可由兩個站點到達。因此,為保證盡可能少的站點和救護車,站點應優先滿足第一部分區域的覆蓋即區域1區域-6、區域10區域-9、區域10-區域11、區域7-區域14區域-4,、區域7-區域15區域-16-區域5 。在此基礎上,區域1的站點的4條分別可到達區域13、3、14、6的備用路線以及區域10的站點能分別到達5條區域8、12、13、15、16的路線可用作在呼叫量大于救護車數量時臨時派遣前往。
4 總結
本文首先根據已知的救護車站點位置以及救護車行駛距離模型檢驗是否滿足響應時間在6分鐘以內的約束,結果表明滿足。經過分析可知,當救護站點為1時是不可能滿足響應時間在6分鐘以內,所以分別檢驗救護站點為2和3時的響應情況,當救護站點為3時滿足救護車響應時間在6分鐘以內。
利用最大覆蓋模型對伊薩卡市呼叫需求點進行更加詳細的區域劃分,并根據影響因素計算各救護車站點的救護車數輛,建立車輛調度模型,當該區域救護車全部出車時,從其他區域調車的情況。

