密封環(huán)圓臺型織構化粗糙表面對潤滑性能的影響*
樊智敏 馬瑞磷 江 峰
(青島科技大學機電工程學院 山東青島 266100)
機械密封是一種廣泛應用于工業(yè)領域的密封裝置,它主要由動環(huán)和靜環(huán)組成,兩環(huán)之間形成一層液膜可以減少端面磨損,同時液膜需要足夠薄來防止過度泄漏。許多學者采用表面織構的方法來提高機械密封的性能,近幾年,表面織構技術已經成功地應用于軸承和密封領域[1-2]。機械密封潤滑膜厚度為微米級,端面粗糙度通常為相同數量級或高一個數量級,因此表面粗糙度對密封性能的影響不容忽視[3-4]。
陳匯龍等[5]采用 Gauss 概率分布模型描述密封端面粗糙度,研究了動壓型機械密封端面粗糙度對密封潤滑性能的影響。呂祥奎等[6]基于 Gauss 分布函數和指數自相關函數,研究了金屬墊片密封結構的粗糙表面特征參數和接觸壓力對密封結構泄漏率的影響。上述研究只研究了單一粗糙度,未考慮織構和粗糙度共同作用的影響。馬晨波等[7-8]考察了粗糙度參數對織構表面摩擦學性能及最優(yōu)織構參數的影響規(guī)律,進而建立考慮粗糙度影響的最優(yōu)參數設計模型對表面織構進行摩擦學設計。陳文杰等[9]考慮潤滑液膜的宏微觀空化效應和微凸體的接觸作用,研究了具有不同粗糙度特征的圓孔型織構化機械密封的摩擦學特性和密封性能。上述研究考慮了織構和粗糙度共同作用的影響,但織構類型均采用圓形織構,存在幾何織構形狀考慮不全面的問題。
本文作者以動靜密封環(huán)接觸面之間的潤滑膜為研究對象,考慮粗糙度的影響,建立在流體動壓潤滑狀態(tài)下圓臺型表面織構的數學模型,對不同織構參數、不同粗糙度參數、不同工況下潤滑膜壓力大小及分布情況進行了研究,旨在提高動靜環(huán)接觸面的潤滑密封能力。
1 幾何模型
圖1為考慮粗糙度參數時圓臺織構微單元的模型圖。構建如圖1所示坐標系。
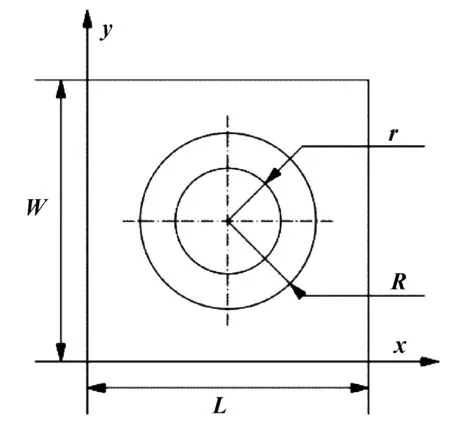
圖1 圓臺織構微單元模型
其中,L、W分別表示微單元在x、y坐標上的長度(假設微單元為正方形),圓臺織構外徑為R,內徑為r,深度為hp。為便于計算分析,假設凹坑織構位于微單元的中心位置。
粗糙織構表面如圖2所示,U為摩擦副表面相對運動方向,織構位于下表面,截面輪廓為梯形。
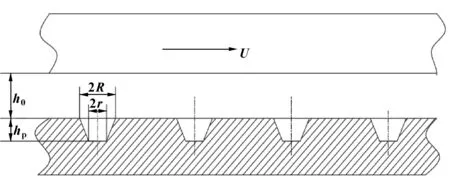
圖2 粗糙織構表面模型
2 數學模型
2.1 建立Reynolds方程
穩(wěn)態(tài)流體動力潤滑狀態(tài)下Reynolds方程可以表示為
(1)
式中:p為潤滑膜壓力;η為運動黏度;ρ為密度;x和y分別為橫和縱坐標;h為潤滑膜厚度;U為下表面沿x方向上的運動速度。
2.2 膜厚方程
對單個圓臺型微凹坑織構建立坐標系,如圖1所示。假設圓臺型凹坑內任意一點(x,y)到凹坑底面中心的距離為s,則:
(2)
不考慮粗糙度影響時,(x,y)的膜厚方程表達式為
(3)
假設粗糙度函數可近似用余弦函數來表示,則:
(4)
式中:wf為粗糙峰峰高;wb為粗糙峰波長。
綜合考慮織構與粗糙度的影響時潤滑膜厚度表達式為
h(x,y)=h1(x,y)-R(x,y)
(5)
2.3 邊界條件
圖3所示為單個凹坑欄示意圖。其中,x軸為運動方向,凹坑欄內微凹坑數為Np。
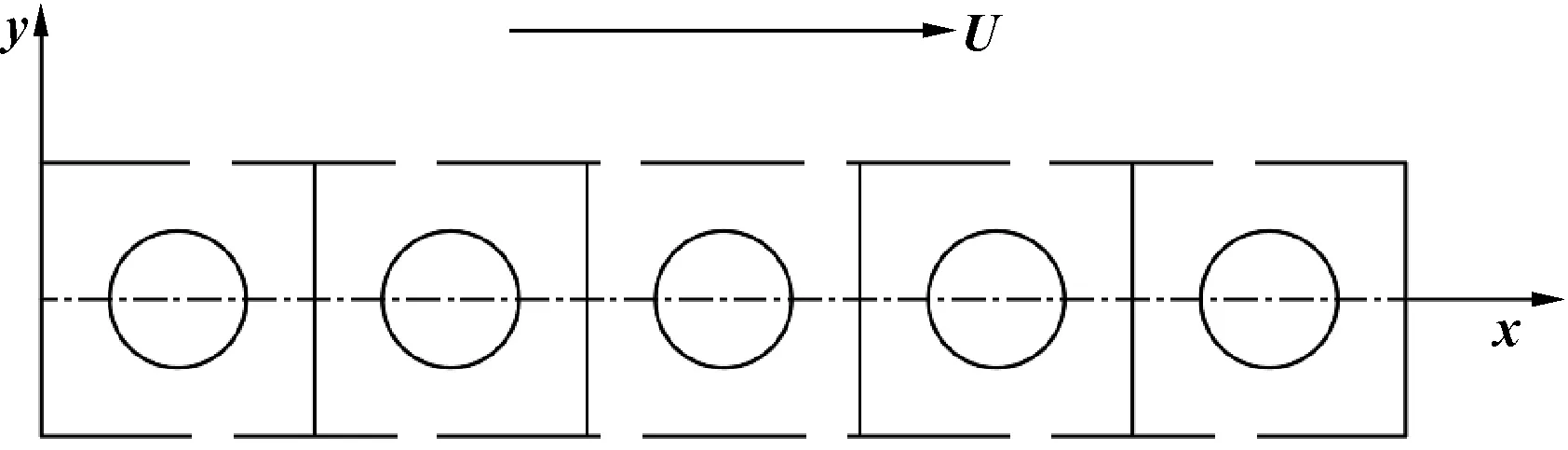
圖3 單個矩形凹坑欄示意
沿x方向,滑塊兩端的邊界壓力為環(huán)境壓力p0;沿y方向,潤滑膜壓力呈周期性分布,即:
(6)
2.4 潤滑膜的平均壓力
單個微坑內潤滑膜的平均壓力表達式為
(7)
式中:lx為滑塊的長度,lx=LNp。
2.5 量綱一化
定義如下量綱一化參數:
(8)
式中:X、Y為量綱一的直角坐標系;H為量綱一潤滑膜的厚度;P為量綱一潤滑膜的壓力;p0為大氣壓;Rp為量綱一圓臺織構外徑。
式(9)為量綱一化Reynolds方程:
(9)
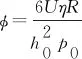
任意一點的量綱一化膜厚方程可由式(10)表示:
(10)
將式(8)代入式(4)得微凹坑欄外表面粗糙度的量綱一化方程為
(11)
式中:Wf=wf/h0,Wb=wb/lx。
將式(8)代入式(5)可得微凹坑織構化粗糙表面潤滑膜的量綱一化膜厚方程:
H(X,Y)=H1(X,Y)-R(X,Y)
(12)
從而,量綱一化邊界條件為
(13)
單個凹坑欄內潤滑膜平均量綱一壓力為
(14)
3 數值計算
3.1 有限差分法求解Reynolds方程
對式(9)采用中心差分格式進行離散化得到最終的計算公式:
APi+1,j+BPi-1,j+CPi,j+1+DPi,j-1-EPi,j=F
(15)
其中,
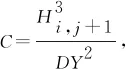
各節(jié)點潤滑膜壓力P(i,j)表達式為
(16)
3.2 松弛迭代法和收斂準則
由式(16)所給出各節(jié)點處的潤滑膜壓力表達式形成一組線性方程,采用超松弛迭代法進行求解,如式(17)所示。
(17)
式中:k為迭代次數;b為松弛因子,其中松弛因子大于1時為超松弛,小于1時為亞松弛[10]。
為了保證迭代的收斂速度,取b=1.2。計算精度的判定如式(18)所示,E為預先設置的誤差限,取E=10-6。迭代收斂條件為
(18)
計算流程如圖4所示。
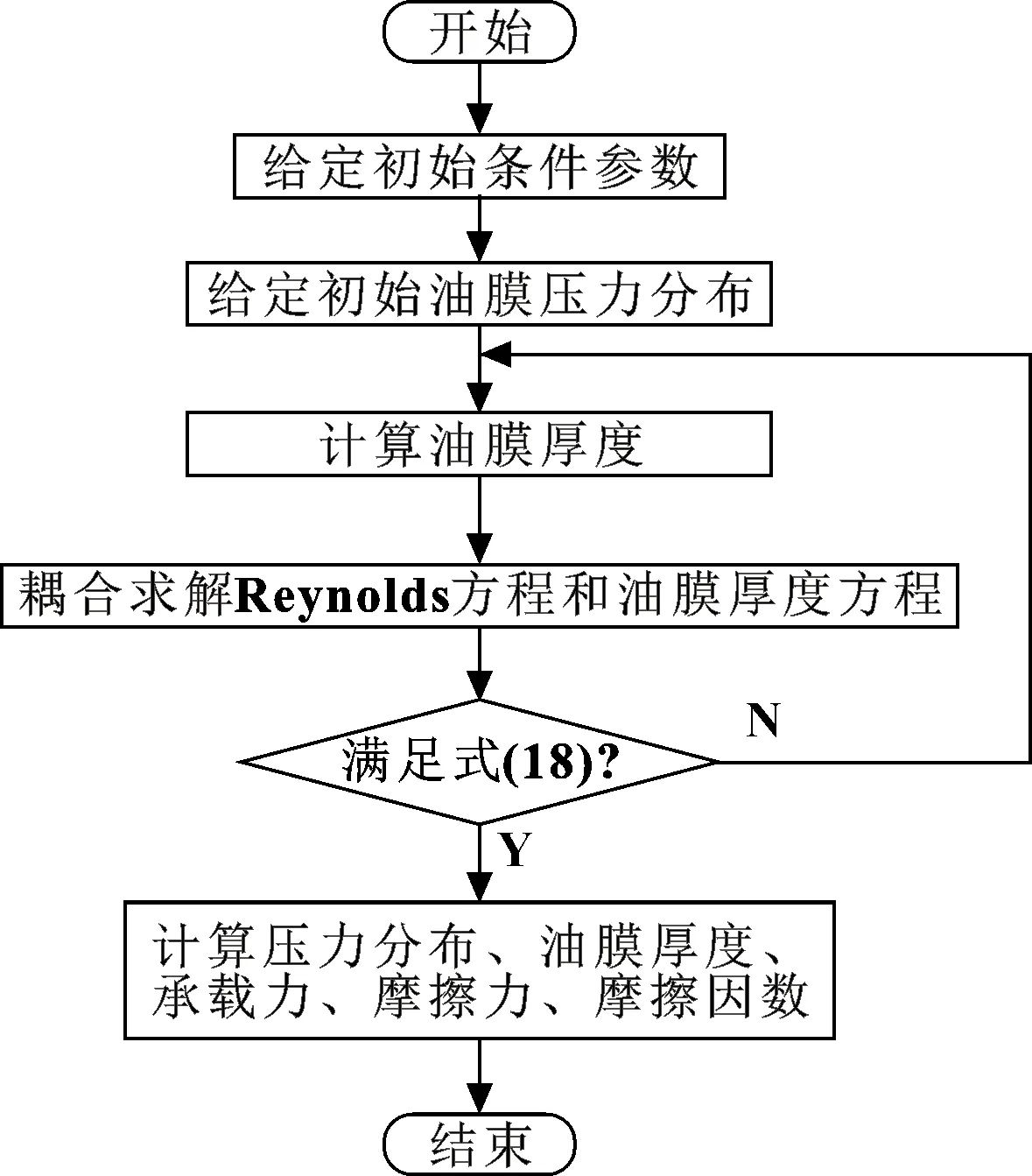
圖4 計算流程
3.3 承載力計算
對于混合潤滑狀態(tài),其總承載能力由兩部分組成:潤滑膜的承載力和粗糙峰的承載力[11]。潤滑膜的承載力如下式:
(19)
在混合潤滑狀態(tài)下,采用Greenwood-William接觸模型[12]求解粗糙峰的承載力,則平均接觸壓力載荷可表示為
pc=KE0F2(λ)
(20)
式中:K=5.318 7×1010·σ2.5;F2(λ)是與粗糙峰高度的概率分布相關的參數;E0代表摩擦副材料的綜合彈性模量。
可得到粗糙峰的承載力為
(21)
則潤滑膜和粗糙峰的總承載力為
D=D1+D2
(22)
3.4 摩擦力與摩擦因數計算
粗糙度存在時的摩擦力也由兩部分組成,即動壓油膜產生的黏性剪切力[13-14]和粗糙峰之間的摩擦力。首先確定剪切力的表達式,再對剪切力積分即可求得摩擦副表面的摩擦阻力,其表達式為
(23)
粗糙峰之間的摩擦力可表示為
(24)
則總摩擦力如式(25)所示:
F=Fy+Fc
(25)
求得承載力和摩擦力以后,摩擦因數可以表示為
μ=F/D
(26)
4 數值結果及分析
文中粗糙織構表面數值模擬主要參數如表1所示。
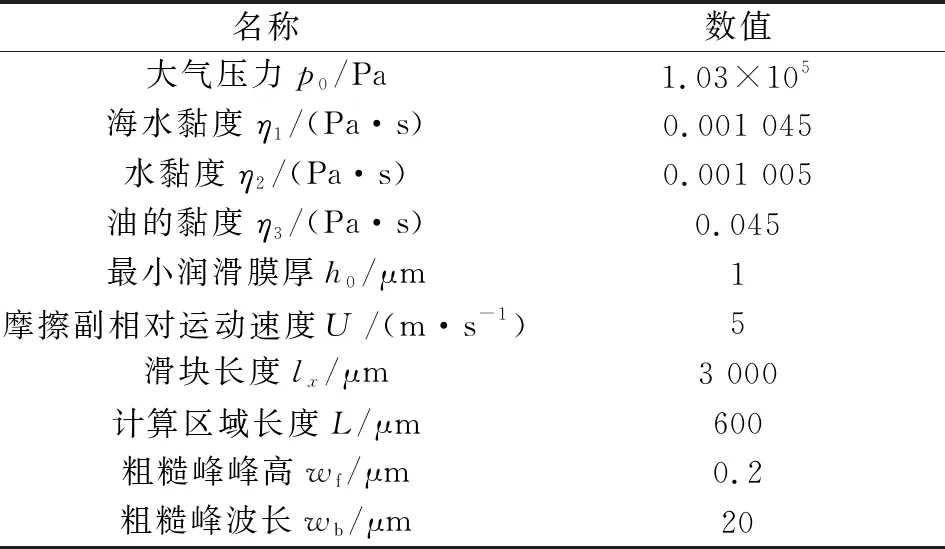
表1 粗糙織構表面數值模擬主要參數
圖5、圖6所示分別為海水為潤滑介質、速度為5 m/s時粗糙織構表面的壓力、膜厚分布規(guī)律。
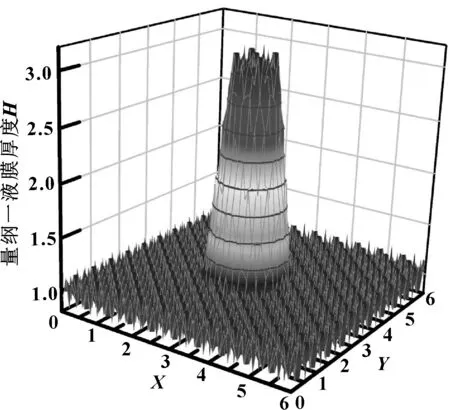
圖5 量綱一潤滑膜厚度分布
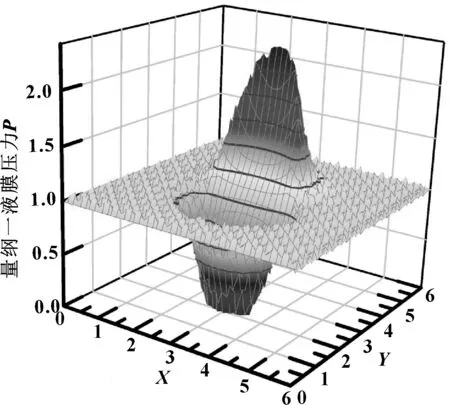
圖6 量綱一潤滑膜壓力分布
4.1 驗證分析
在水壓2.5 MPa,彈簧壓力0.15 MPa,轉速3 000 r/min 工況下,使用模型進行仿真計算,通過解析計算的數據來驗證仿真模型的正確性。由表2可見,膜壓的仿真值與理論值誤差率為0.8%,符合實際情況,驗證了模型的可行性[15]。

表2 膜壓的理論數據與仿真數據比較
4.2 圓臺型織構幾何參數對液膜壓力的影響
通過對比3種類型的潤滑介質(油、海水和水),綜合分析不同潤滑介質條件下,圓臺型織構幾何參數對液膜壓力的影響。
4.2.1 織構間距對液膜壓力的影響
取微凹坑織構深度為2 μm,其大、小半徑分別為100、50 μm,摩擦副的相對運動速度為5 m/s。圓臺型微凹坑間距對潤滑膜量綱一平均壓力的影響如圖7所示。
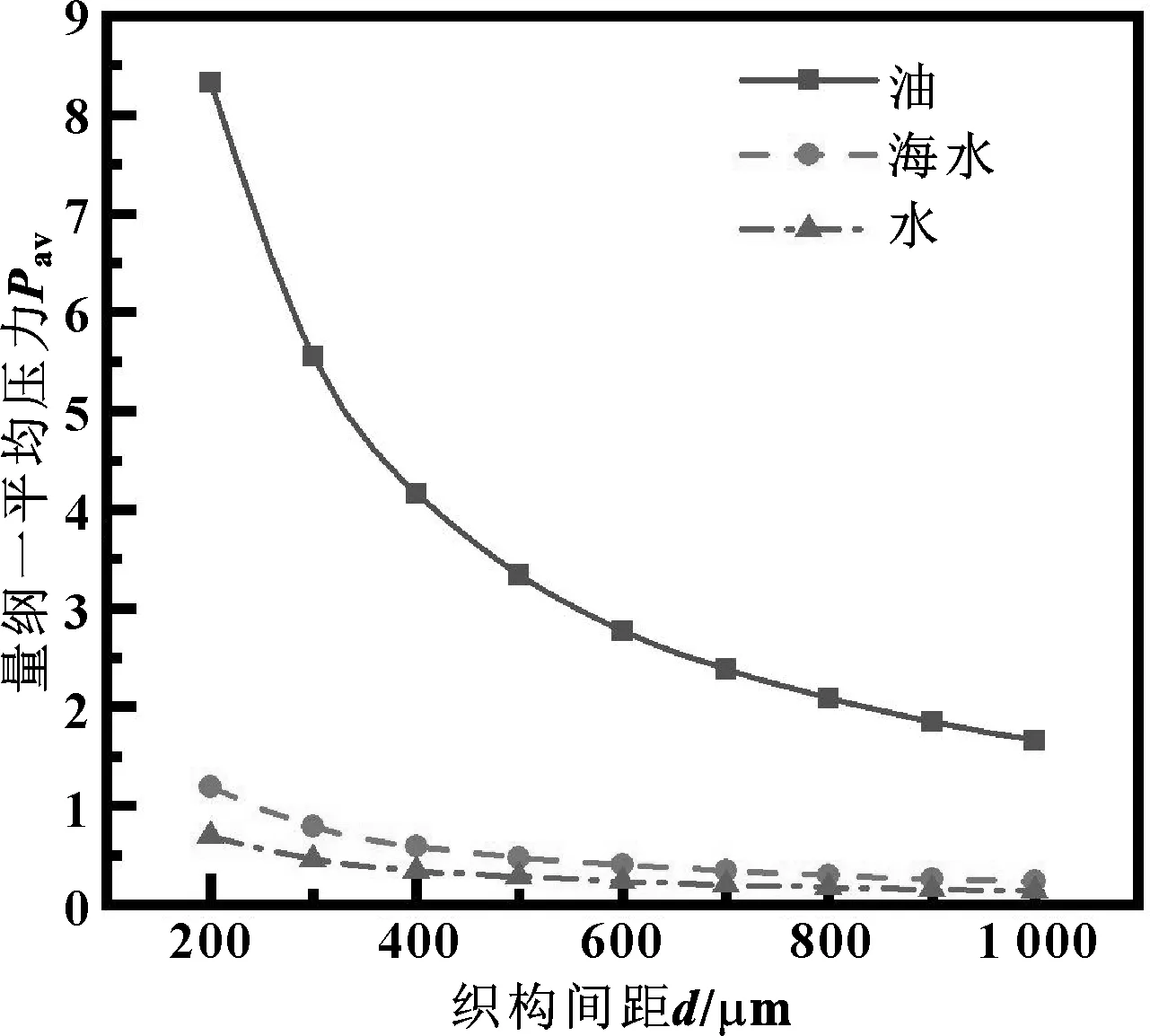
圖7 微凹坑間距對量綱一平均壓力的影響
由圖7可知,隨著微凹坑間距的增大,潤滑膜的量綱一平均壓力逐漸減小。當間距較大時,潤滑膜的量綱一平均壓力變化趨于穩(wěn)定。當間距增加到600 μm,繼續(xù)增大間距對平均壓力幾乎無影響。原因是計算域軸向長度一定,間距越大,織構的數量就越少,織構所產生的流體動壓就越小。這與文獻[16]中曲線趨勢基本一致,說明文中方法可行。
4.2.2 織構深度對液膜壓力的影響
取微凹坑織構間距為600 μm,其大、小半徑分別為100、50 μm,摩擦副的相對運動速度為5 m/s。圓臺型微凹坑深度對潤滑膜量綱一平均壓力的影響如圖8所示。
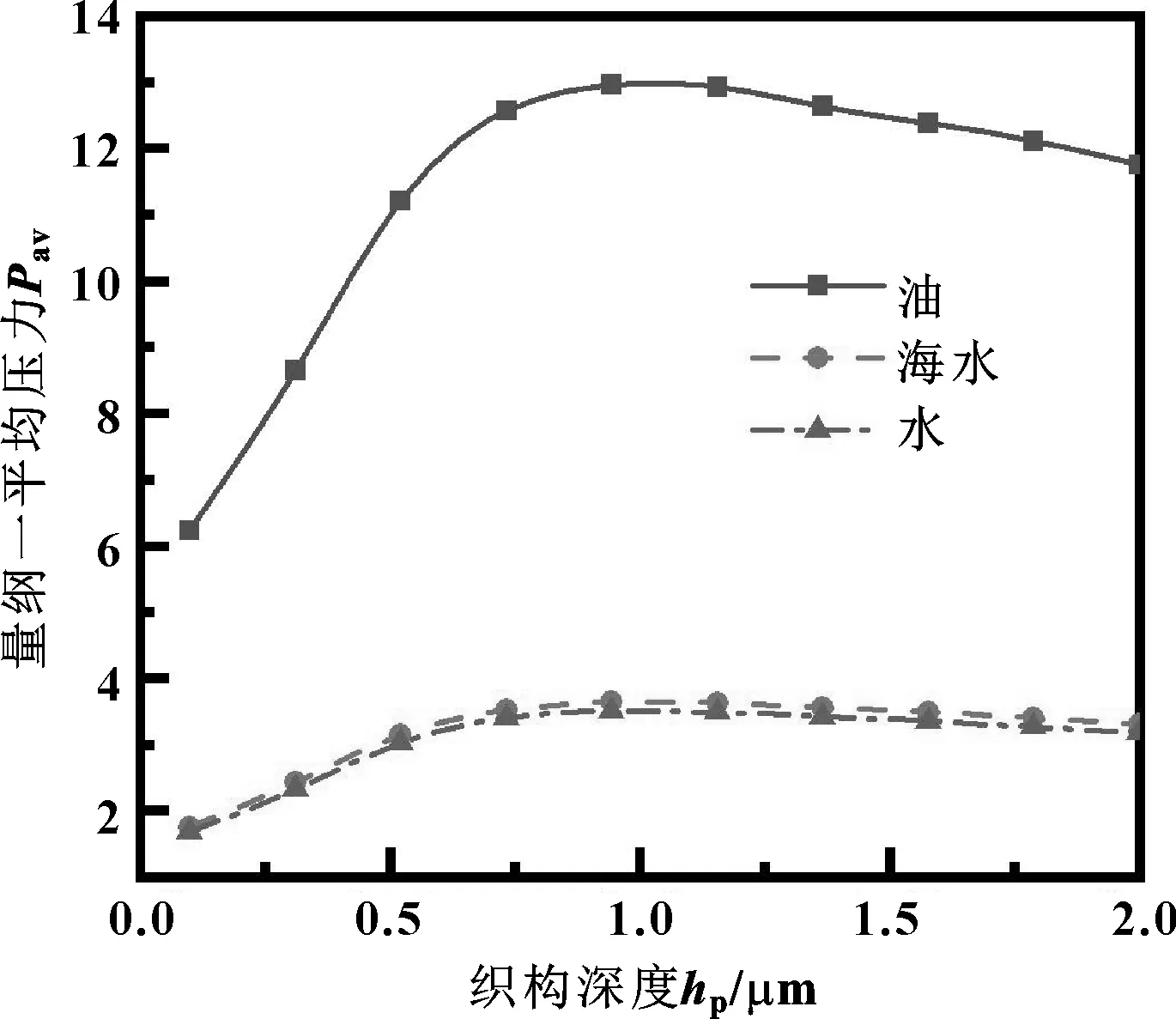
圖8 微凹坑深度對量綱一平均壓力的影響
由圖8可知,量綱一平均壓力隨微凹坑深度的增大呈現先增大后減小的趨勢,可以得出,存在一個最佳的織構深度,即織構深度取1 μm時,量綱一平均壓力最大。這與文獻[16]中曲線趨勢基本一致。
4.2.3 織構大徑對液膜壓力的影響
取微凹坑織構間距為600 μm,織構深度為2 μm,小半徑為50 μm,摩擦副的相對運動速度為5 m/s。圓臺型微凹坑織構大徑對潤滑膜量綱一平均壓力的影響如圖9所示。
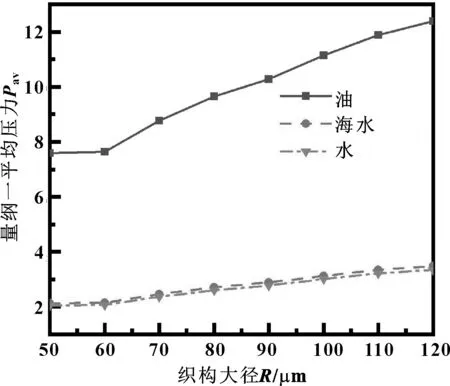
圖9 微凹坑織構大徑對量綱一平均壓力的影響
由圖9可知,織構小徑不變時,量綱一平均壓力隨大徑的增大而逐漸增大。當織構大徑值趨近小徑值時,即圓臺型織構可近似看作底面半徑為50 μm的圓柱型織構,此時量綱一平均壓力最小,增長率也較小;當織構大徑大于60 μm時,大徑值每增加10 μm,油、海水、水潤滑3種條件下量綱一平均壓力分別增加0.69、0.19、0.18。
4.2.4 織構小徑對液膜壓力的影響
取微凹坑織構間距為600 μm,織構深度為2 μm,大半徑為100 μm,摩擦副的相對運動速度為5 m/s。圓臺型微凹坑織構小徑對潤滑膜量綱一平均壓力的影響如圖10所示。
由圖10可知,織構大徑不變時,量綱一平均壓力隨小徑的增大而逐漸減小。當織構小徑值趨近0時,即圓臺型織構近似為圓錐型織構,此時量綱一平均壓力最大,且平均壓力的降低速率較小。當織構小徑大于0時,小徑值每增加10 μm,油、海水、水潤滑3種條件下量綱一平均壓力分別降低0.51、0.14、0.13。
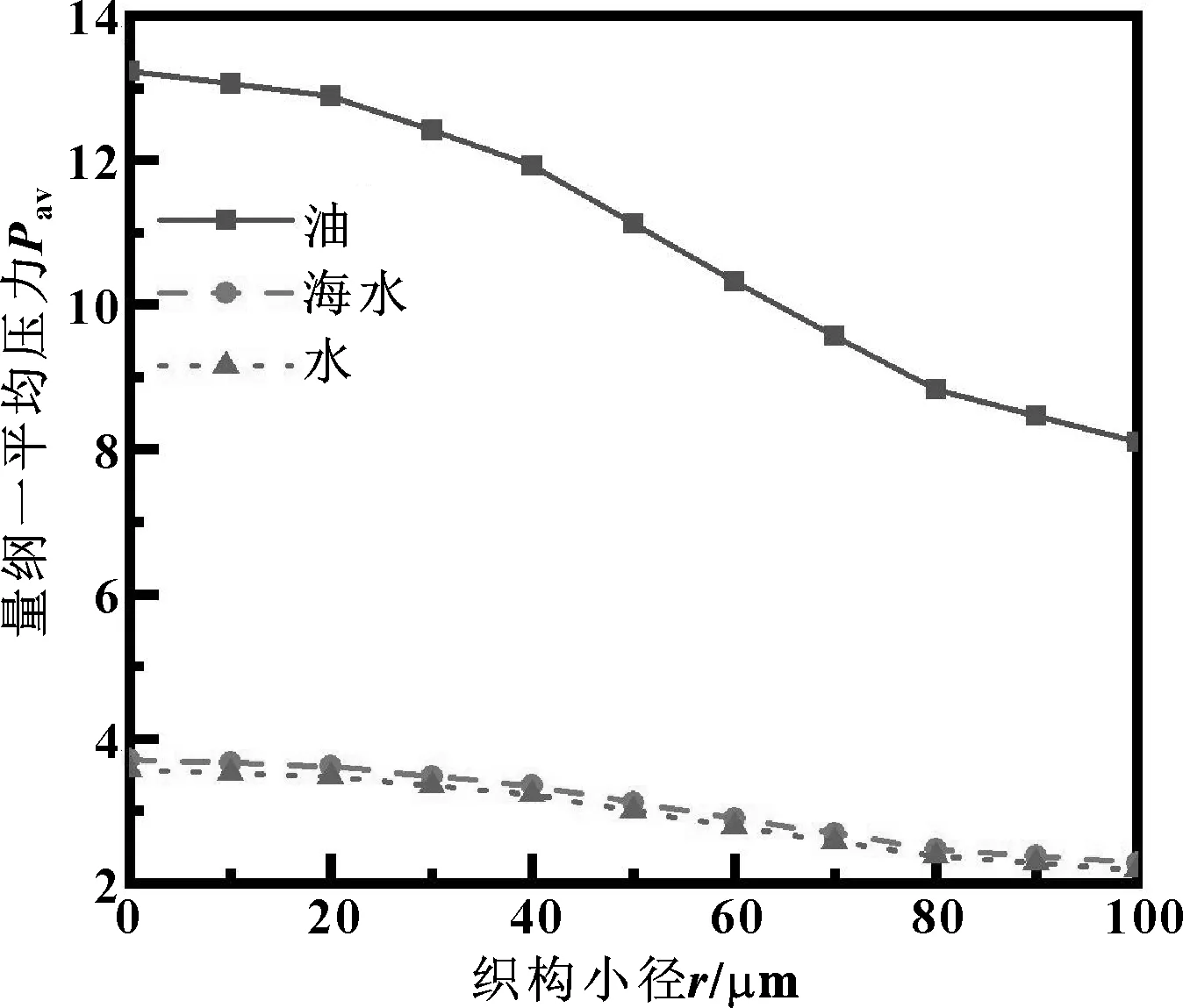
圖10 微凹坑織構小徑對量綱一平均壓力的影響
綜合圖7—10結果,可以總結出,相同工況下,油作為潤滑介質時的量綱一平均壓力最大,海水次之,水作為潤滑介質時的量綱一平均壓力最小。原因是3種潤滑介質的黏度不同[17],黏度越大,液膜動壓效應越明顯,因此量綱一平均壓力越大;3種潤滑條件下,量綱一壓力變化趨勢基本一致,說明最優(yōu)織構參數不隨潤滑介質黏度的變化而變化。
4.3 余弦模型粗糙峰的影響
4.3.1 粗糙峰峰高對液膜壓力的影響
圖11示出了不同織構深度時,粗糙度峰高對平均壓力的影響。
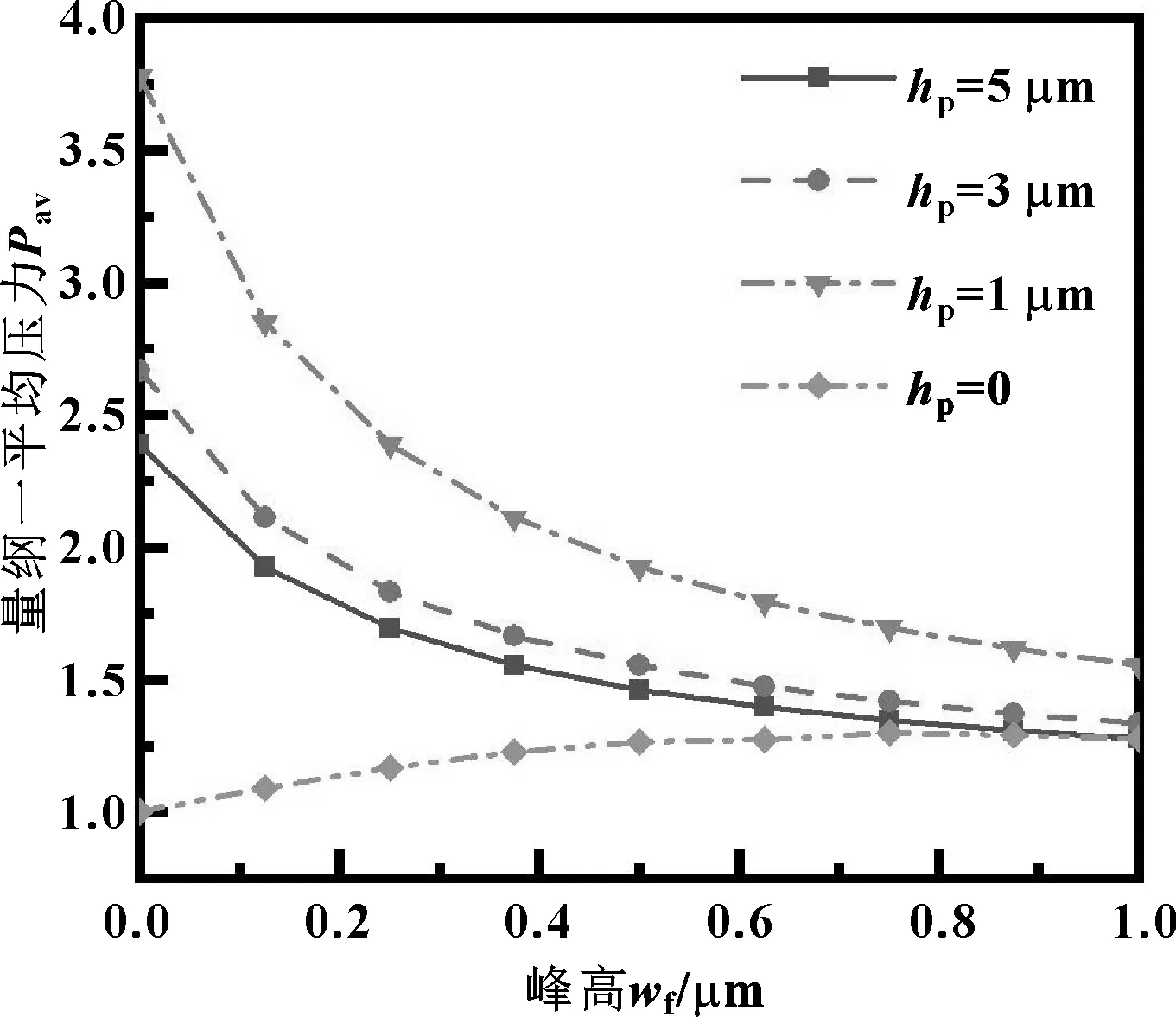
圖11 粗糙峰峰高對量綱一平均壓力的影響
由圖11可知,當織構深度為0,即僅存在粗糙度的情況下,隨著峰高的增大,平均量綱一壓力呈現先增大后減小的趨勢,且存在最佳峰高即0.7 μm,使平均壓力達到最大;當織構深度大于0時,平均壓力隨峰高的增大而減小,原因是織構與粗糙度同時存在,平均壓力受到這兩方面因素的影響,織構產生的流體潤滑效應受到粗糙峰的抑制,且峰高越大,抑制力越強,因此表面織構在實際的生產應用中,粗糙峰應盡可能地小。
4.3.2 粗糙峰波長對液膜壓力的影響
圖12示出了不同織構深度時,粗糙峰波長對平均壓力的影響。
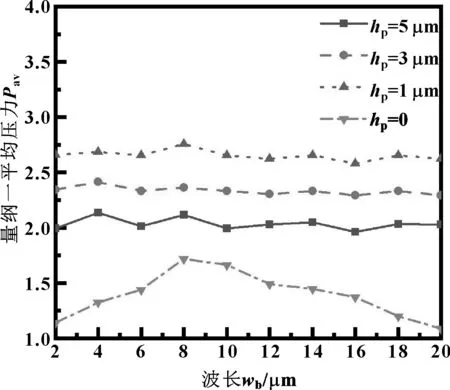
圖12 粗糙峰波長對量綱一平均壓力的影響
由圖12可知,當織構深度為0,即僅存在粗糙度的情況下,隨著波長的增大,平均量綱一壓力先增大后減小,且存在最佳波長即8 μm,使平均壓力達到最大;當織構深度大于0時,平均壓力基本不隨波長的增大而變化,與文獻[12]中曲線趨勢基本一致,原因是平均壓力受粗糙度和織構兩方面影響,當微凹坑織構的深度較大時,峰高相比于織構深度較小,對承載力的影響也較小。
5 結論
(1)圓臺型織構的參數特征對以油、海水和水為介質的端面液膜壓力有較大影響,相鄰兩織構的間距越大,液膜壓力越小;圓臺型織構大徑越大,液膜壓力越大,當大徑近似等于小徑時,即為圓柱型織構,此時的液膜壓力最小;織構小徑越大,液膜壓力越小,當小徑近似為0時,即為圓錐形織構,此時液膜壓力最大;存在最佳織構深度使液膜壓力最大。
(2)相同的情況下,密封端面油的平均膜壓要高于海水的平均膜壓,水的平均膜壓相對最小,但油的黏度值過大會使摩擦力增大,溫度升高,容易造成潤滑膜破裂。因此選用合適的織構參數和潤滑介質可以大大提高動靜環(huán)接觸端面的潤滑性能。
(3)無織構情況下,存在最佳峰高和波長使端面平均膜壓最大;存在圓臺型織構的情況下,粗糙峰峰高越大,端面平均膜壓越小,而粗糙峰波長對端面平均膜壓的影響較小。因此,存在粗糙度參數與織構參數的最優(yōu)組合使端面平均膜壓達到最大值。

