弧面分度凸輪機構分度期潤滑狀態及油膜研究*
趙 帥 尹明富 朱 洋
(天津工業大學機械工程學院 天津 300387)
弧面分度凸輪機構是一種性能優越并且適用于高速分度的新型蝸桿式凸輪傳動機構,又被稱為福開森機構[1]。目前,國內外對弧面分度凸輪機構的研究發展很快,在空間嚙合原理、運動和幾何特性分析、動力學研究等方面都已經取得了一定的研究成果,為該機構的設計和生產提供了強大的理論基礎[2]。隨著國內機械制造業的飛快發展,空間凸輪機構成為不可或缺的核心傳動件,但是缺少對弧面分度凸輪機構潤滑性能的研究。
弧面分度凸輪機構能夠按照特定規律進行周期性的分度和轉位動作,在機構長時間的運動時,弧面分度凸輪工作輪廓曲面與轉盤滾子曲面之間接觸區域的位置在分度期時容易出現失效情況[3-4],直接影響其傳動效率、平穩性能以及使用壽命。因此,本文作者研究弧面分度凸輪機構分度期潤滑狀態及形成動態潤滑油膜厚度。
1 弧面分度凸輪機構數學模型
1.1 弧面分度凸輪機構工作原理
常規的弧面分度凸輪機構由弧面分度凸輪和轉盤組成。當弧面凸輪勻速轉動,在其分度期會推動轉盤轉動,在其停歇期2個相鄰的圓柱滾子會停留在凸輪凸脊的兩側。機構在分度期嚙合的過程中,由于弧面凸輪與圓柱滾子2個線接觸摩擦面的相對運動產生的動壓效應,會形成彈流潤滑油膜,進而達到保護機構的目的[5-6]。
1.2 建立機構的研究模型
在機構中建立的坐標系如圖1所示:O0X0Y0Z0為與機架相連的定坐標系,O1X1Y1Z1為與弧面凸輪相連的動坐標系,O2X2Y2Z2為與轉盤相連的動坐標系,O′0X′0Y′0Z′0為與機架相連的輔助定坐標系。
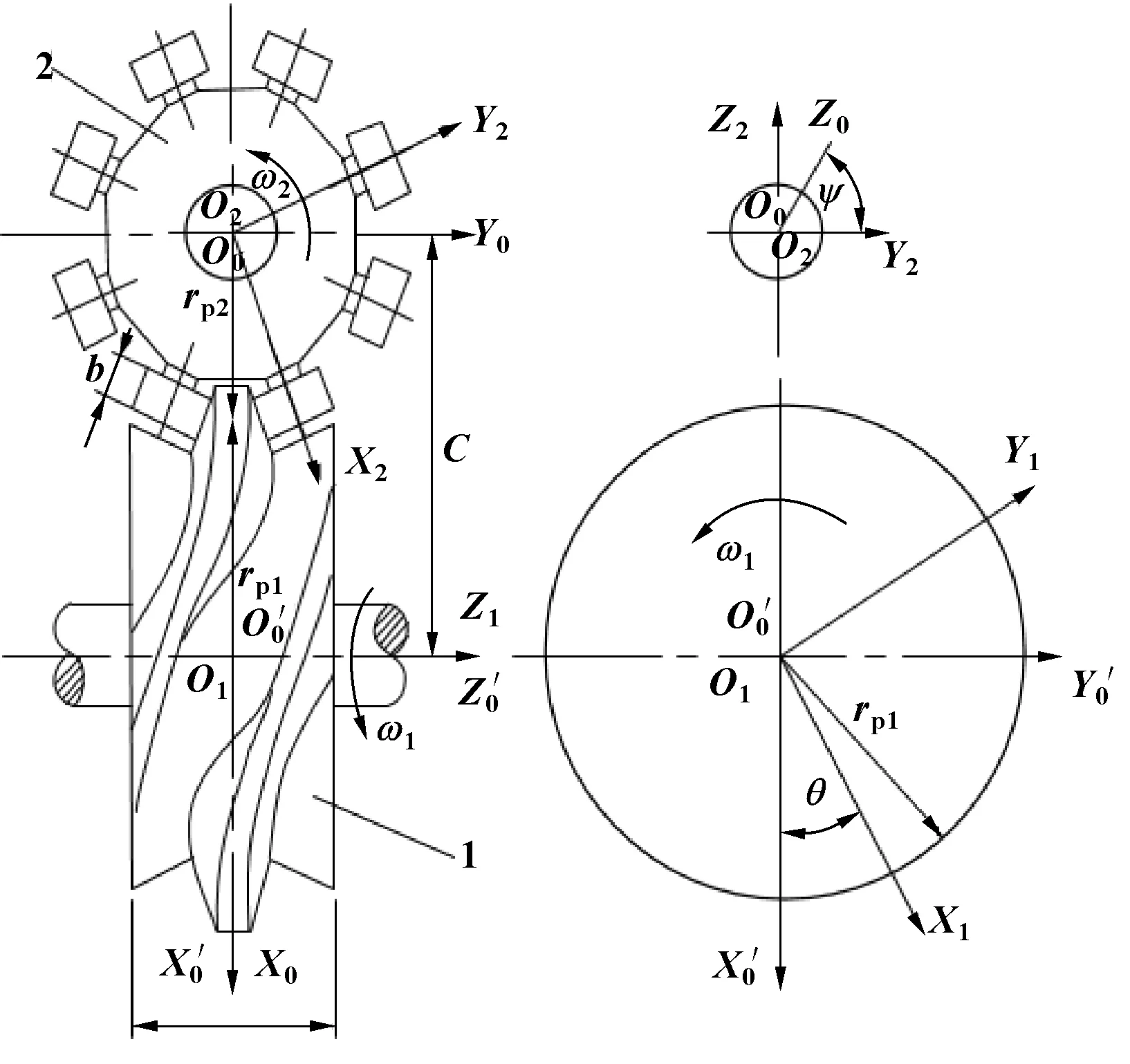
圖1 機構中建立的笛卡爾坐標系
通過轉盤圓柱滾子的曲面方程,選擇一定的從動件的運動規律,以微分幾何和旋轉變量為基礎,根據空間包絡曲面的共軛原理,推導計算出弧面凸輪的工作廓面方程[7]。
表1為研究模型所采用的主要運動幾何參數。

表1 主要運動幾何參數
2 穩態工況下相關潤滑參數求解
2.1 彈流潤滑油膜厚度計算理論
弧面凸輪與圓柱滾子2個線接觸摩擦面在進行相對運動時,會形成彈流潤滑油膜。根據文獻,可采用Hamrock-Dowson公式進行機構分度期嚙合過程的最小油膜厚度Hmin的分析計算[8-9]。
(1)

在穩態工況下,一般的傳動機構所選用潤滑油參數為η0=20×10-3Pa·s,α=2×10-8m2/N[10-11]。
根據公式分析,在機構保證潤滑油參數一定的情況下,形成彈流油膜的厚度主要跟機構共軛接觸處的卷吸速度、誘導主曲率、接觸應力有關。
2.2 求解卷吸速度u
假設弧面凸輪與滾子之間的運動為純滾動,弧面凸輪的速度為u1,圓柱滾子速度為u2,則
u1=ω1·rp1
(2)
u2=ω2·rp2
(3)
式中:ω1、ω2分別為弧面凸輪和圓柱滾子的角速度,rad/s;rp1、rp2分別為弧面凸輪和圓柱滾子的節圓半徑,mm。
卷吸速度u為分度盤滾子接觸點的絕對速度,表達式為
u=(u1+u2)/2
(4)
2.3 求解誘導主曲率
兩曲面在接觸點K處不發生根切的情況下,誘導法曲率在沿瞬時接觸線方向為0,即誘導主曲率其中的一個解為0,對另一個誘導主曲率的求解過程如下:
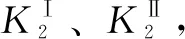
(5)
式中:β為圓柱滾子曲面坐標參數;φ為滾子的位置角。

(6)
(7)
其中
式中:ε2為轉盤角加速度;ω1、ω2分別為弧面凸輪與滾子的角速度;c為機構的中心距。
根據歐拉公式可知,誘導主曲率方向為沿垂直于接觸線切線方向,其值為
(8)
3 機構接觸應力σ的算法推導
3.1 理論推導接觸應力
弧面凸輪與圓柱滾子在分度期嚙合時,2個曲面的接觸形式為線接觸,在接觸面會有接觸應力的產生。假設把弧面凸輪與從動滾子簡化成圓柱體與平面相接觸,以從動件圓柱滾子為研究對象,對機構分度期凸輪副的受力進行分析,在嚙合過程中,凸輪副會產生法向壓力Fn,Fn是影響接觸應力大小的重要參數。
3.1.1 推導求解凸輪副法向壓力Fn
以從動件為研究對象,在S2坐標系中,將法向力Fn分解為沿圓周方向的圓周力Ft,沿分度盤軸向的軸向力Fa和沿分度盤節圓半徑的徑向力Fr,如圖2所示。

圖2 受力分析
圓周力與法向力的夾角為β(β為圓柱滾子柱面坐標參數),而從動件分度盤的節圓半徑與法向力是垂直關系,所以Fr=0。因此
(9)
其中:
Fa=Fttanβ
(10)
利用機構的功能守恒原理對圓周力進行求解,將從動滾子簡化成一個質點,穩態工況下,弧面凸輪近似做勻速轉動,電機的輸入功率全部轉化為圓周力在分度期所做的功。當電機輸入功率為P時,弧面分度凸輪機構在一個分度期內所消耗的功為w=Ptd,其中td機構的轉位時間,可知:

(11)
式中:φ為分度盤角位移;dφ為轉盤角位移瞬時增量。
機構選定從動件的運動規律為修正正弦加速度運動,對式(11)進行變形求解得最大圓周力
(12)
式中:ω1為弧面凸輪轉速;θh和φh分別為弧面凸輪和分度盤的分度角。
因此可以推導求得在一個分度期內嚙合處所受圓周力的表達式為
(13)
將式(10)、(12)、(13)代入式(9)中即可得到凸輪副法向壓力Fn。
3.1.2 求解凸輪副接觸應力σ
在嚙合過程中,主動件與從動件相接觸的輪廓形狀復雜,因此簡化計算不會影響結果,初始接觸長度B取滾子的高度。研究模型機構材料采用42CrMo,穩態工況下,彈性模量E1=E2=210 GPa,泊松比為μ1=μ2=0.3。根據彈性接觸的Hertz理論對機構分度期凸輪副產生的接觸應力進行求解[12]:
(14)
式中:Fn為凸輪副的法向壓力。
將已知各參數代入(14)中,即可求凸輪副接觸應力σ。
3.2 接觸應力算法可行性仿真實驗驗證
利用ANSYS軟件對建立的機構研究模型進行有限元分析,采用靜力學分析模塊對機構在分度期嚙合過程中的接觸應力進行求解,對主動件添加初始條件弧面分度凸輪轉速為n=300 r/min,材料屬性與理論推導條件相同,機構分度期接觸應力分布結果如圖3所示。

圖3 弧面分度凸輪機構應力云圖
利用MATLAB對接觸應力算法進行仿真計算,與有限元分析保持相同的參數條件不變,表2為所得不同嚙合位置接觸應力四舍五入后的部分數據。
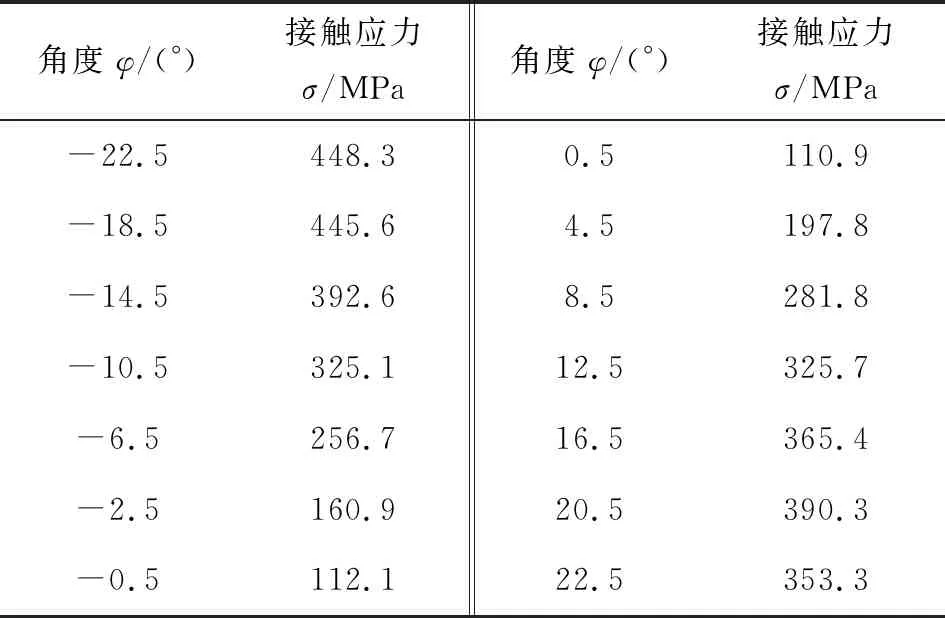
表2 不同嚙合位置接觸應力
2種不同仿真方法的數據結果相符合,在誤差允許范圍內,證明接觸應力新算法推導可行。
4 實例仿真實驗及潤滑狀態分析
弧面分度凸輪機構是一種中高速、承載能力強的傳動機構。保證研究模型其他參數不變,改變主動件弧面分度凸輪的轉速,研究不同轉速條件下,機構的潤滑狀態及動態潤滑油膜的形成。
4.1 不同轉速對接觸應力的影響
根據上文推導出的接觸應力算法,利用MATLAB編寫程序,對不同嚙合點的接觸應力進行仿真計算,主動件的轉速n分別設定為300、600、900 r/min。仿真結果如圖4所示。
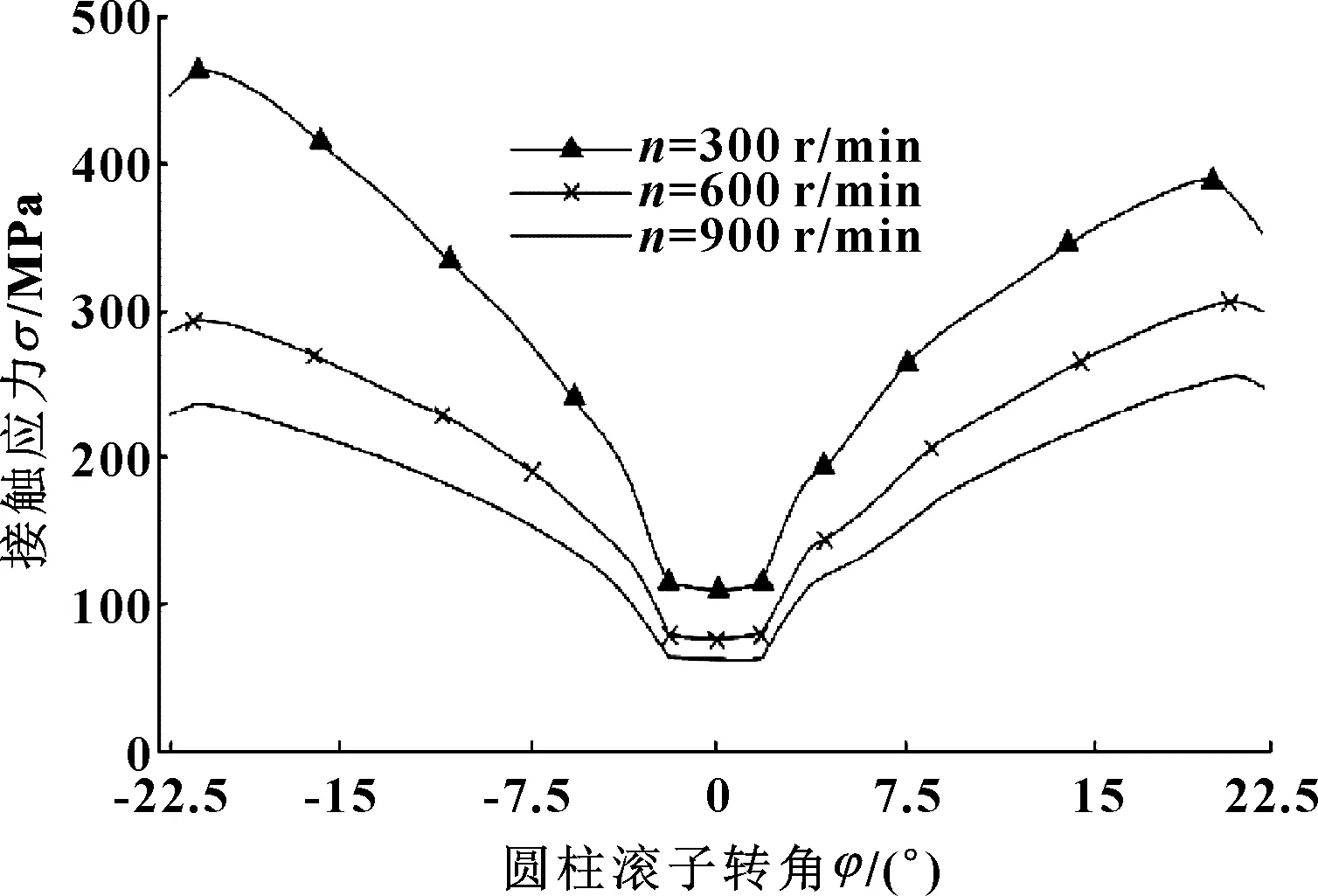
圖4 不同轉速對接觸應力的影響
凸輪轉速越大,機構嚙合處接觸應力越小,凸輪轉速的改變,不會改變接觸應力變化的整體走向。
4.2 不同轉速對形成彈流潤滑油膜的影響
4.2.1 最小油膜厚度仿真
基于Hamrock-Dowson公式對不同嚙合位置形成的最小油膜厚度進行仿真,主動件的轉速n同樣分別設定為300、600、900 r/min。不同轉速的仿真結果如圖5—7所示,X、Y分別代表凸輪工作廓面的位置坐標。

圖5 300 r/min條件下的最小膜厚
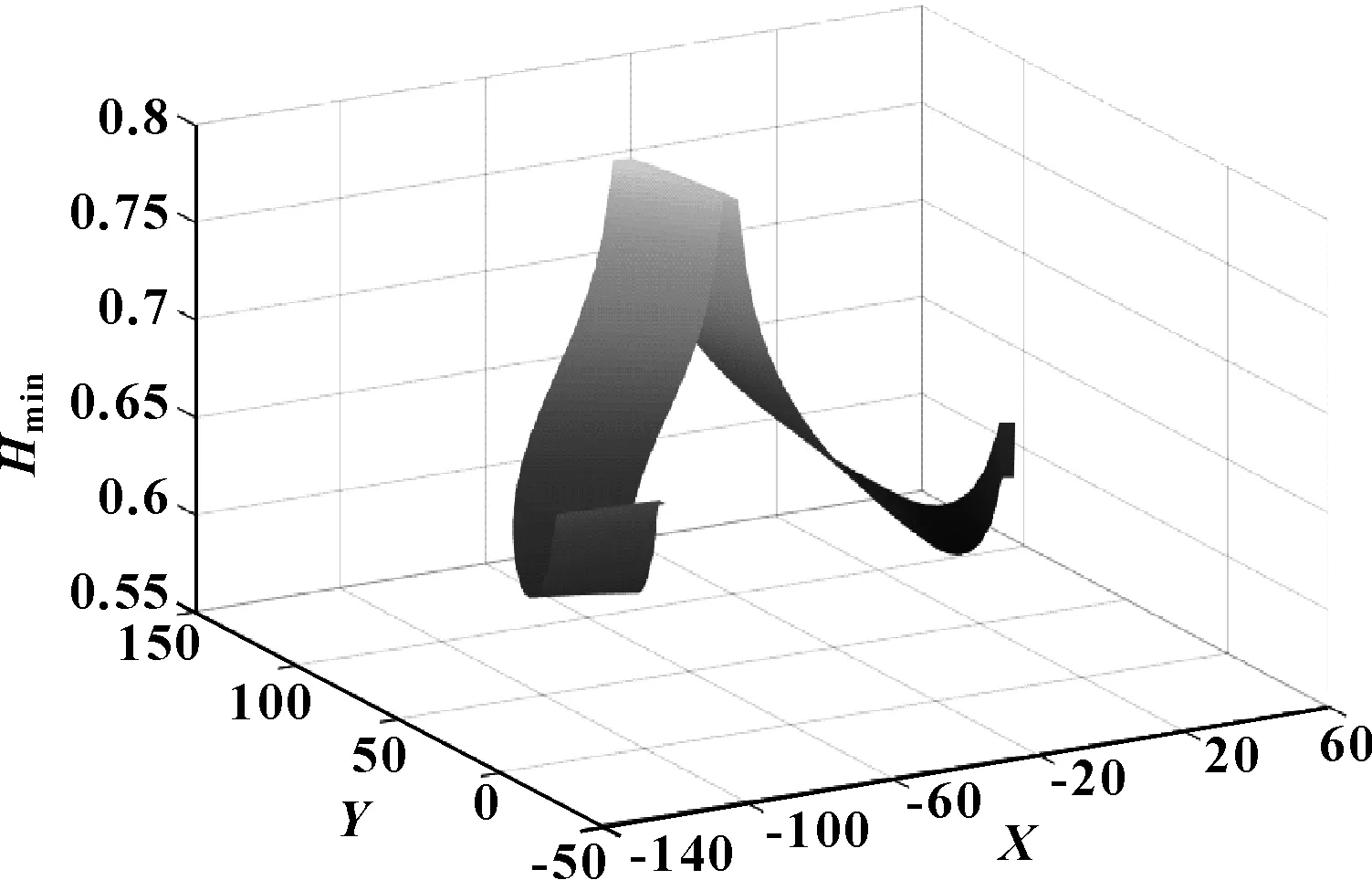
圖7 900 r/min條件下的最小膜厚
從圖中可以得出,凸輪轉速越大,形成的最小油膜厚度越大。
4.2.2 膜厚比計算
為了更加準確地分析機構嚙合過程的潤滑狀態,引用膜厚比概念對彈流潤滑油膜進行分析。依據前人的實驗數據總結[13-14],如圖8所示,當膜厚比λ<0.7(A區),沒有彈流潤滑油膜產生,屬于干摩擦狀態,機構損傷嚴重。0.7≤λ≤1.5(B區),屬于混合潤滑狀態,成膜率小于50%,機構在傳動過程中會產生滑動,降低機構壽命。1.5≤λ≤3(C區),成膜率大于50%,嚙合過程工作表面的損傷會大大減小。λ≥3(D區),屬于流體潤滑狀態,不會發生摩擦,但是目前工業技術難以達到。
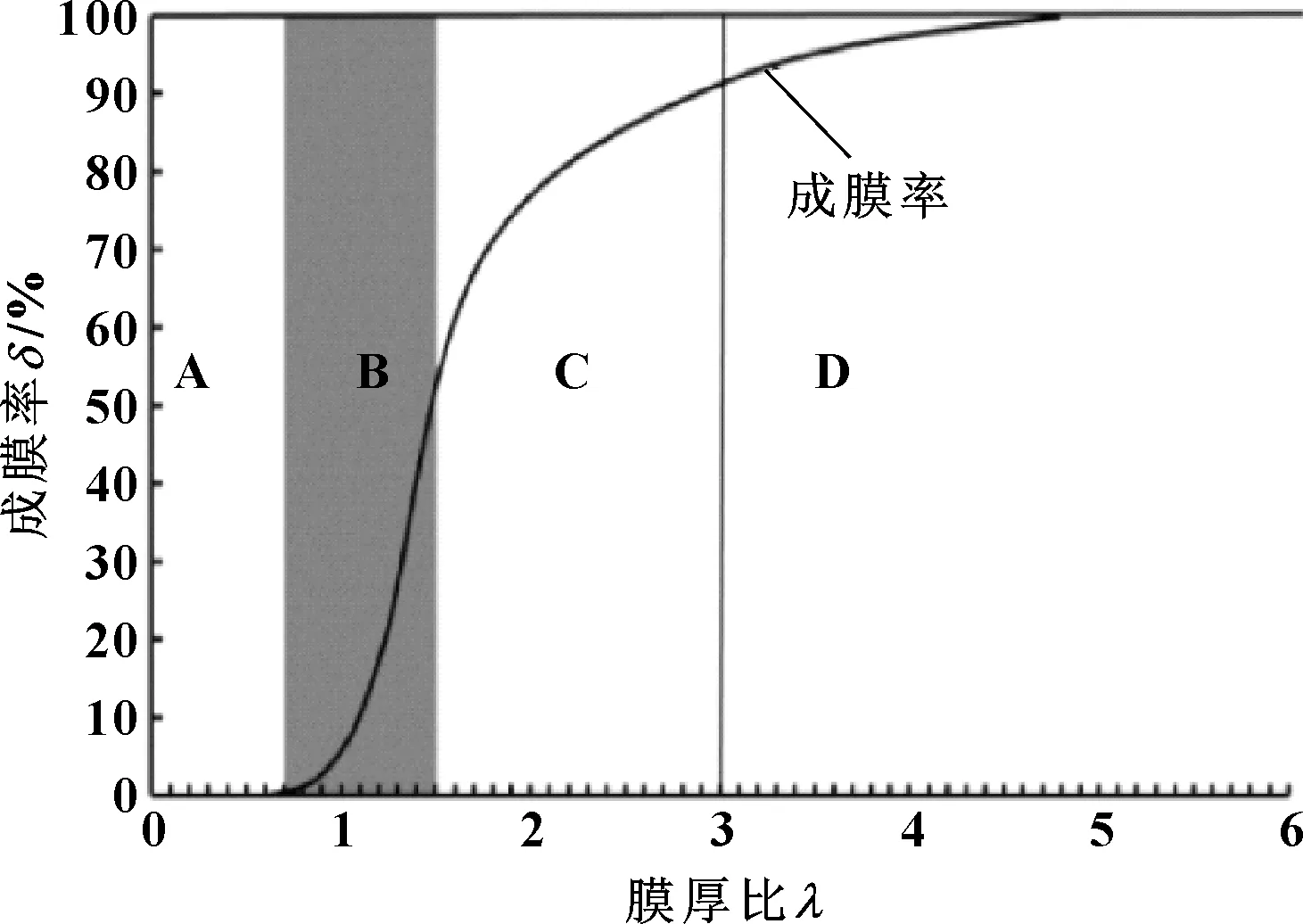
圖8 成膜率與膜厚比關系
膜厚比計算公式為
(15)
式中:σ1、σ2分別為從動件和主動件表面粗糙度均方根偏差,分別取0.16、0.3 μm。
對不同轉速下的膜厚比進行求解,結果如圖9所示。
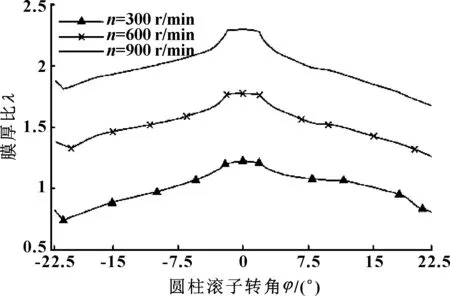
圖9 不同轉速條件的膜厚比
當機構低速傳動時,分度期嚙入段及嚙出段膜厚比λ<0.1,成膜率極低,基本不能形成彈流潤滑油膜,處于干摩擦狀態,需要進行脂潤滑。凸輪轉速越大,越有利于形成彈流潤滑油膜。
4.3 機構潤滑狀態仿真結果分析
從圖4和圖9得出的結果可知,接觸應力和膜厚比的整體走向成反向。
分度期初期,機構嚙合過程為單滾子嚙合,期間接觸應力較大,膜厚比較小,很難形成彈流潤滑油膜。分度期達到中期,機構進行雙滾子嚙合,接觸應力減小,形成的最小油膜厚度增加,成膜率也出現峰值。分度期末期,機構脫離雙滾子嚙合繼續進行單滾子嚙合,接觸應力逐漸增大,形成的油膜厚度減小。
因此,在分度期初期以及分度期末期,也就是滾子剛進入嚙合和即將離開嚙合的區域,機構的潤滑狀態較差,最難形成潤滑油膜,最易出現磨損失效。
5 結論
(1)針對弧面分度凸輪機構嚙合特點,對分度期潤滑狀態進行分析,推導出兩共軛曲面嚙合過程受力的求解方法,并進行可行性驗證。分析表明,在穩態工作情況下,卷吸速度、誘導主曲率以及接觸應力是影響潤滑油膜形成的關鍵因素。
(2)采用數值分析法對機構嚙合分度期的最小油膜厚度進行求解。結果表明,在機構低轉速的情況下,嚙入段和嚙出段極難形成彈流潤滑油膜,為提高弧面分度凸輪機構的潤滑性能提供理論依據。

