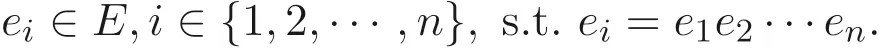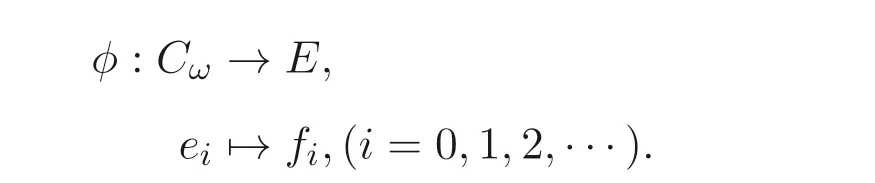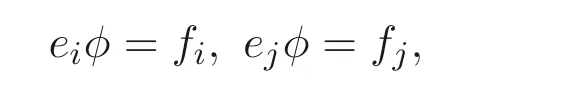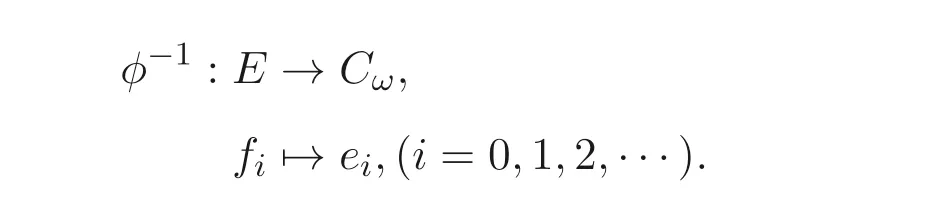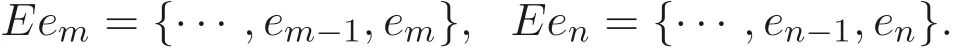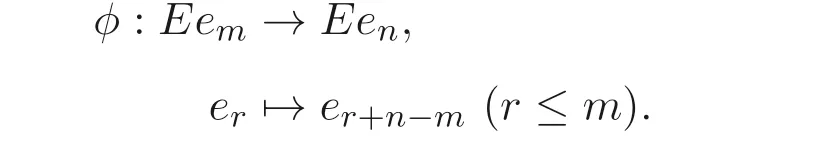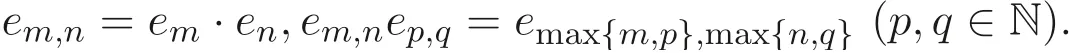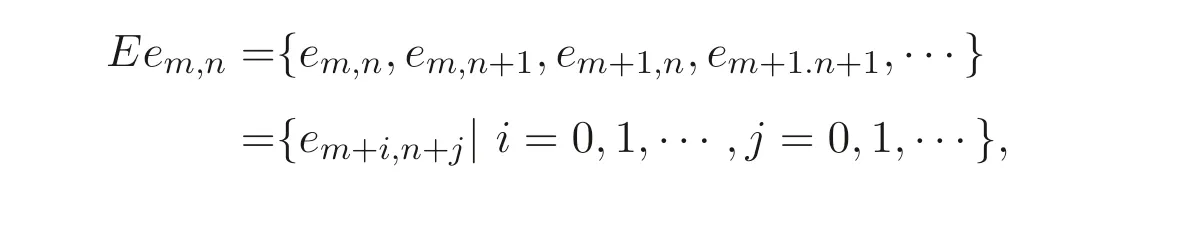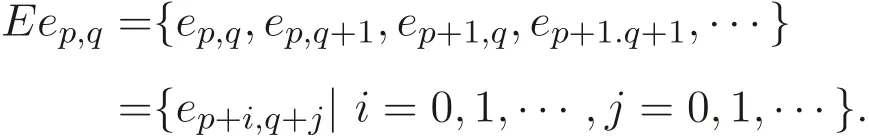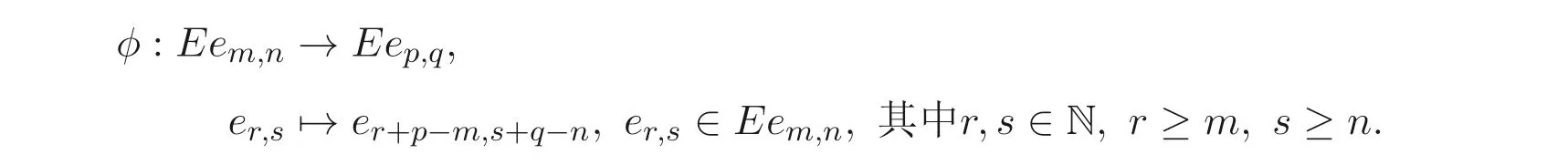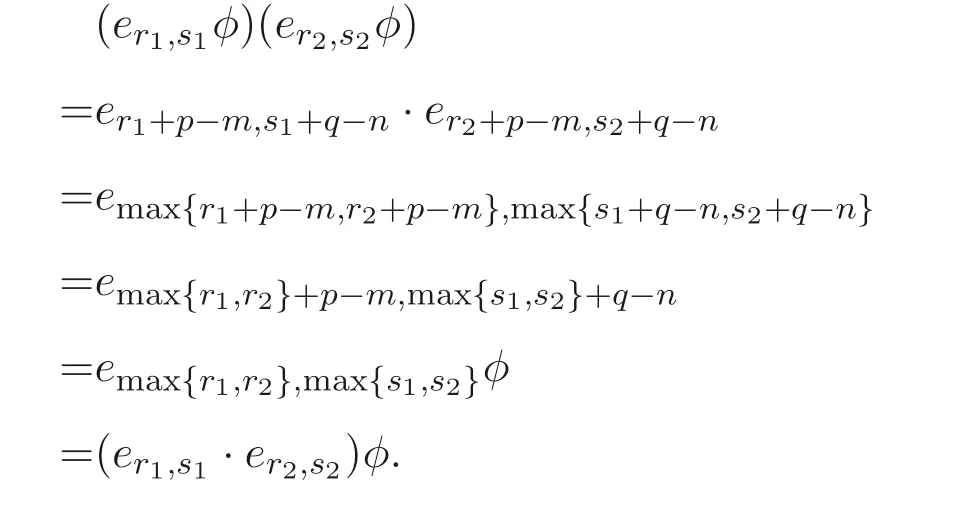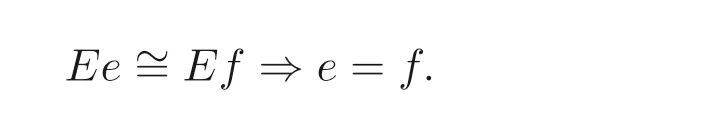關于一致半格的注記

程彥亮, 邵勇

(西北大學數學學院, 陜西 西安 710127)

1 引言

設(S,·) 是交換半群. 若對任意a ∈S有a2=a成立, 則稱(S,·) 為半格. 設(S,·)為半格, 在S上定義偏序如下:

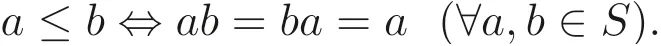
由偏序的定義, 對任意a,b ∈S, 易知,ab是a與b的最大下界. 若存在c ∈S,有a ≤c ≤b ?c=a或c=b, 則稱b覆蓋a或a被b覆蓋, 記為a ?b[2]. 設X是偏序集(S,≤) 的非空子集, 若存在a ∈X, 使得對任意x ∈X, 有x ≤a ?x=a,則稱a為X的極小元. 若存在b ∈X, 使得對任意y ∈X, 有b ≤y ?b=y, 則稱b為X的極大元. 設(S,·) 為半格, 對任意M ?S,M ?=?, 若M含有極小元, 則稱S滿足極小條件. 若M含有極大元, 則稱S滿足極大條件. 設(S,≤) 為偏序集, 若對任意a,b ∈S,總有a ≤b或b ≤a成立, 則稱S為鏈. 若鏈滿足極小條件, 則稱該鏈為良序鏈.

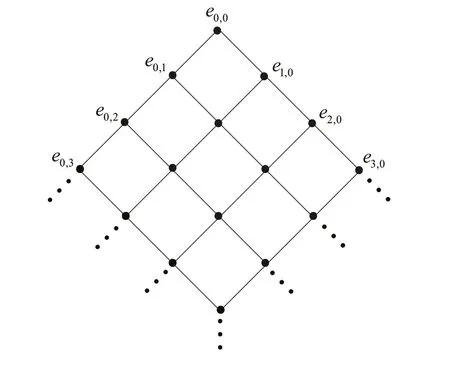
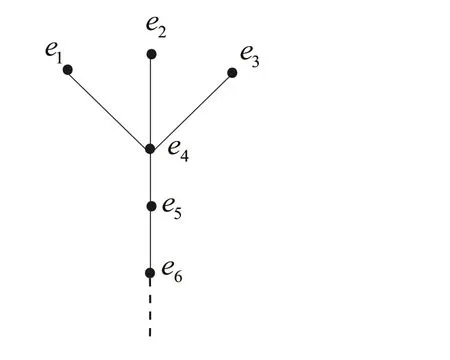
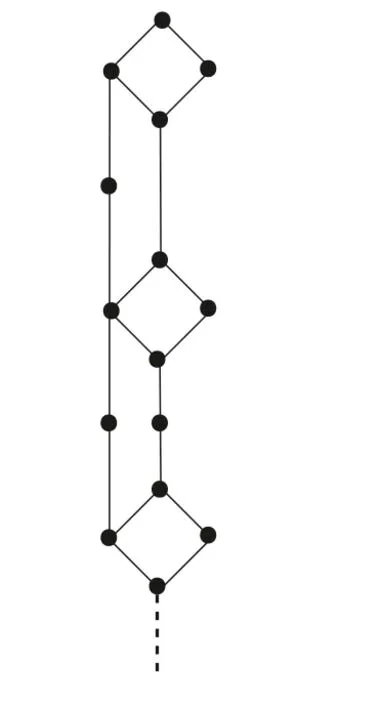
定義1.1[1]設E是鏈, 若對e ∈E, 集合{x ∈E|x

定義1.2[3]設E是半格, 若對任意e ∈E, 有Ee={f ∈E|f ≤e}, 則稱Ee為由e生成的主理想.

定義1.3[4]設E是半格, 若對任意e,f ∈E, 有Ee～=Ef, 則稱E為一致半格.

若Ee～=Ef ?e=f, 則稱E為反一致半格.

例1.1設E=Cω={e0,e1,e2,···}, 其中e0>e1>e2>···, 則對任意en ∈Cω,由en生成的主理想為Cωen={en,en+1,en+2,···}. 易知對任意em,en ∈Cω, 其中m,n ∈N={0,1,2,···}, 有Cωem～=Cωen成立. 因此Cω為一致半格.

定義1.4[1]設S是半群, 若對任意a ∈S,a有唯一的逆元, 則稱S為逆半群. 若在逆半群S上, 格林D關系為泛關系, 即D=S×S, 則稱S為雙單逆半群.

由文獻[5] 知, 若S是雙單逆半群, 則由S的冪等元形成的半格為一致半格, 而半格為一致半格的逆半群并非都是雙單逆半群. 例如, 一致半格自身是逆半群, 但是它不是雙單逆半群. 但是, 的確存在一個這樣的雙單逆半群, 即由該一致半格對應的Munn半群. 由文獻[1] 知, 不同類型的一致半格所對應的雙單逆半群具有不同的結構, 例如,半格同構于Cω的雙單逆半群為雙單逆ω- 半群. 文獻[3] 通過半格之間的一個類型積構造了一致半格M(r). 文獻[6] 探究了半格同構于M(r) 的雙單逆半群的結構. 顯然,Cω是滿足極大條件的無限鏈, 本文探究了滿足極大條件的無限鏈與Cω的關系, 并且給出了滿足極大條件的無限鏈的等價刻畫. 討論了極小條件與一致半格以及極大條件與反一致半格的關系.

若E為半格,E中僅含有一個元素e, 即E={e}, 則稱E為平凡半格[7], 易知,平凡半格既是一致的又是反一致的. 下文中所提到的半格, 若無特別說明, 均為至少包含兩個元素的非平凡半格.

2 主要結論

引理2.1設E是一致半格, 則E必是無限的.

證明假設E是有限的, 不妨設E={e1,e2,··· ,en},那么存在

因此, 對任意k ∈{1,2,··· ,n}, 有ei ≤ek. 故ei是E的最小元. 進而,Eei={ei}. 然而對任意ej ∈E,(j ?=i), 則有Eej至少包含兩個元素{ei,ej}, 因此|Eej|≥2, 顯然,Eei?Eej,(i ?=j), 這與E是一致的矛盾, 故E是無限的.

由該引理知, 一致半格必是無限的, 因此在探究極大條件與一致半格的關系時, 僅從無限的角度出發.

引理2.2任何滿足極大條件的無限鏈同構于Cω, 即它是一致半格.

證明設E是滿足極大條件的無限鏈, 則E含有最大元, 記為f0.

通過以下方式定義映射φ:Cω →E.

首先,Cω={e0,e1,e2,···}, 其中e0>e1>e2>···, 令φ將Cω中的最大元映到E中的最大元, 即e0φ=f0.

然后, 由E是無限鏈知,E {f0} ?=?. 又由E滿足極大條件知, 存在唯一的f1∈E {f0}, 使得對任意的x1∈E {f0}, 有x1≤f1. 因此, 令φ將e1∈Cω映到E{f0}中的最大元, 即e1φ=f1.

以此類推知,E {f0,f1,··· ,fi?1} ?=?. 又由E滿足極大條件知, 存在唯一的fi ∈E{f0,f1,··· ,fi?1}, 使得對任意的xi ∈E{f0,f1,··· ,fi?1}, 有xi ≤fi. 因此,令φ將ei ∈Cω映到E{f0,f1,··· ,fi?1}中的最大元, 即eiφ=fi.

綜上所述,

容易驗證,φ是良定義的, 下證φ是雙射:

對于任意ei ?=ej,(i ?=j), 有

由E是鏈知, 當i ?=j時, 有fi ?=fj成立, 從而eiφ ?=ejφ, 故φ是單射.

要證φ是滿射. 只需說明以上取法能夠取遍E, 即證對于E{f0}中任意元素, 總存在另一元素將其覆蓋, 這是因為, 若對任意f ∈E{f0}, 存在唯一元素f′∈E, 使得f ?f′, 那么f就是集合E{f0,f1,··· ,f′}的最大元, 又由f的任意性知, 以上取法取遍E.

要證對于E{f0}中的任意元素, 總存在另一元素將其覆蓋, 由E中元素的任意性知, 只需證對于任意f′∈E, 存在唯一的元素f ∈E, 使得f ?f′. 假設E中不存在f, 使得f ?f′成立, 那么集合E{f0,f1,··· ,f′} ?E沒有最大元. 又由E是無限鏈知,E{f0,f1,··· ,f′}沒有極大元, 且E{f0,f1,··· ,f′}?=?. 這與E滿足極大條件矛盾, 從而對任意的f′∈E, 存在唯一的f ∈E, 使得f ?f′.

因此以上取法能夠取遍E. 故對于任意的f?∈E, 總存在k ∈N, 使得fk=f?, 由于存在ek ∈Cω, 使得ekφ=fk=f?, 因此φ是滿射, 故φ是雙射. 下證φ和φ?1都是保序的:

定義

對任意fi,fj ∈E,其中i ?=j. 不妨設i

由以上引理可知, 若E是滿足極大條件的無限鏈, 那么E是一致半格. 而一致半格并非都是滿足極大條件的無限鏈. 如下例2.1:

例2.1設E是鏈,并且E的鏈序同構于整數,即E={··· ,e?2,e?1,e0,e1,e2,···},并且···

證明對于任意em,en ∈E,m,n ∈Z={··· ,?2,?1,0,1,2,···}, 則有

定義映射

容易驗證,φ是同構映射, 故Eem～=Een. 因此,E是一致半格.

顯然,E是無限鏈, 但E不滿足極大條件, 這是由于E自身沒有最大元.E的Hasse 圖如圖1:

圖1

例2.2設E=Cω×Cω, 其中Cω={e0,e1,e2,···},e0>e1>e2>···, 則E是一致半格, 并且滿足極大條件, 但E不是無限鏈.

證明設E=Cω×Cω={em,n|m,n ∈N}, 其中

E的Hasse 圖如圖2:

圖2

對于任意em,n,ep,q ∈E, 則有

類似的,

定義映射

容易驗證,φ是雙射, 下證φ是同態映射:

對任意er1,s1,er2,s2∈Eem,n, 其中ri,si ∈N,ri ≥m,si ≥n,i=1,2.

從而φ是同構映射, 因此E是一致半格, 顯然E有最大元e0.0, 并且E的任意非空子集都含有極大元, 因此E滿足極大條件, 但E不是無限鏈.

以上例子說明, 一致半格不一定為滿足極大條件的無限鏈.

由文獻[1] 知, 滿足極小條件的反一致半格必為良序鏈. 由例2.2 表明, 滿足極大條件的一致半格未必是無限鏈.

定理2.1設E是滿足極大條件的半格, 則E是無限鏈當且僅當E是含有幺元的一致半格, 并且每一個主理想都是鏈.

證明設E是一致半格,|E|≥2. 由引理2.1 知,E是無限的. 由于E含有幺元,并且每一個主理想都是鏈. 設幺元為e, 則E=Ee, 即E是由e生成的主理想, 故E是無限鏈.

另一方面, 若E是滿足極大條件的無限鏈, 由引理2.2 知,E是一致半格. 由于E是無限鏈, 且滿足極大條件, 因此,E含有幺元. 顯然,E的每一個主理想都是鏈.

該定理中的任何條件不可缺失, 若E不滿足每一個主理想都是鏈, 則由例2.2 知,E=Cω×Cω,E包含幺元e0,0, 并且E是滿足極大條件的一致半格, 易見,E不是無限鏈.

若E不含有幺元, 設E={e1,e2,e3,e4,...},E的Hasse 圖如圖3:

圖3

由圖3 可知,E有3 個極大元, 故E不含有幺元, 顯然,E是滿足極大條件的一致半格, 并且每一個主理想均為鏈, 但E不是無限鏈.

對于定理2.1 而言, 條件“E滿足極大條件” 是必要的. 一方面, 若E是含有幺元的一致半格, 并且每一個主理想都是鏈, 由引理2.1 知,E是無限的, 又由E=Ee知,E是無限鏈, (e是E的幺元). 另一方面, 若E是無限鏈, 則E可能是反一致的半格,例如,E是一個鏈序同構于非負整數的無限鏈. 即使E包含幺元, 并且每一個主理想都是鏈,E也未必是一致半格. 如下例:

則E是含有幺元的無限鏈, 且每一個主理想都是鏈, 但E不是一致半格.

證明顯然, 在(1) 式所定義的偏序下,E是無限鏈, 從而E的每一個主理想均為鏈, 又由對于?(q,m)∈E(q ≥0, m ≥0),

(i) 如果q=0,m ≥0, 那么(q,m)=(0,m)≤(0,0);

(ii) 如果q>0,m ≥0, 那么(q,m)≤(0,0).

因此, (0,0) 是E的幺元, 從而E是含有幺元的無限鏈, 下證E不是一致的:

假設E是一致的, 則對任意(q,m),(r,n)∈E, 有E(q,m)～=E(r,n), 設φ是E(q,m) 到E(r,n) 的同構映射. 只需取(q,m) = (q,0),(q ?= 0), (r,n) = (r,rε), 考慮E(q,0) 和E(r,rε),E(q,0) 有最大元(q,0),E(r,rε) 有最大元(r,rε), 由同構映射保序, 故φ將(q,0) 映到(r,rε). 由于集合{x ∈E|x< (r,rε)}沒有最大元, 由定義1.1知, (r,rε) 沒有緊接后元, 集合{x ∈E|x< (q,0)}(q ?= 0) 有最大元(q,1), 從而(q,0)有緊接后元, 這與φ是同構映射矛盾, 故E不是一致半格.

經過上述分析, 定理2.1 中的條件缺一不可, 由例2.3 知, 該定理中的條件“E滿足極大條件” 是必要的.

在文獻[1] 中, 探討了極小條件與反一致半格的關系, 類似地, 由定理2.1 探究了極大條件與一致半格的關系, 現在繼續討論一致半格與極小條件以及反一致半格與極大條件的關系.

定理2.2E是滿足極小條件的一致半格當且僅當E是平凡半格(|E|=1).

證明首先, 若E是平凡半格, 設E={e}, 顯然,E是一致的. 由E的非空子集只能是自身, 從而極小元為e, 故E是滿足極小條件的一致半格.

另一方面,設E是一致半格,并且滿足極小條件.假設E不是平凡半格,即|E|≥2.由于E滿足極小條件, 從而E包含唯一的極小元e, 這是因為, 假設E包含兩個不同的極小元e,f, 則有ef ≤e,ef ≤f, 由于e,f都是極小元, 從而ef=e,ef=f,故e=f. 因此,E包含唯一的極小元e. 進而, 由e生成的主理想Ee={e}. 由E不是平凡半格, 故存在f ∈E,f ?=e, 則由f生成的主理想Ef至少包含兩個元素{e,f},從而Ee?Ef. 這與E是一致半格矛盾, 故E必為平凡半格.

由文獻[1] 知, 設E是有限半格, 若E為鏈, 則E必是反一致的. 接下來探究E是非鏈的情況.

引理2.3若E是非鏈的有限半格, 則E既不是一致的也不是反一致的.

證明設E是非鏈有限半格, 由引理2.1 知, 非平凡一致半格一定是無限的, 故E不是一致的. 下證E不是反一致的:

假設E是反一致的, 由于E是有限半格, 故E滿足極小條件, 因此,E是滿足極小條件的反一致半格, 則E是良序鏈, 這與E是非鏈的矛盾. 因此E不是反一致的.

定理2.3若E是滿足極大條件的反一致半格, 則

證明若|E|< +∞, 即E是有限半格, 假設E不是鏈, 即E是非鏈的有限半格,由引理2.3 知,E不是反一致的, 矛盾. 從而,E是鏈.

另一方面, 若E是鏈, 假設E是無限的, 即E是無限鏈, 由E滿足極大條件, 即E為滿足極大條件的無限鏈, 又由引理2.2 知,E是一致半格, 這與E是反一致的矛盾,從而E是有限的, 即|E|<+∞.

由以上定理可知, 設E是滿足極大條件的反一致半格, 則E只可能出現兩種情況,一種是有限鏈, 另一種是非鏈的無限半格.

例2.4設E是半格,E的Hasse 圖如圖4:

圖4

由圖4 可知, 對于任意e,f ∈E,(e ?=f), 有Ee?Ef, 即

由定義1.4 可知,E是反一致半格, 顯然,E滿足極大條件, 從而E是滿足極大條件的反一致半格. 由圖4 可見,E是無下界的非鏈半格, 即E是非鏈無限半格.

上述例子表明, 滿足極大條件的反一致半格是非鏈的無限半格. 易知, 任何有限鏈都是滿足極大條件的反一致半格.