回歸教學(xué)原點 突破思維障礙*
——以兩道解幾題求解為例

江蘇省新海高級中學(xué) (222006) 徐 方 江蘇省連云港市錦屏高級中學(xué) (222021) 殷長征

1 問題提出

解析幾何突出考查學(xué)生的運算能力，在教學(xué)過程中學(xué)生普遍反映運算量大，教師也說難教，解析幾何是高中數(shù)學(xué)教與學(xué)繞不開的一道思維坎：由于不良的思維習(xí)慣導(dǎo)致在思維過程中對正確思維的抑制而作用產(chǎn)生的思維定勢，具體表現(xiàn)為：將用代數(shù)方法解決幾何問題簡單地理解為運算，忽視對圖形幾何特征的挖掘和對曲線概念的合理利用，沒有真正領(lǐng)悟解析幾何的思維方法—先形后數(shù).

針對上述思維坎形成的原因應(yīng)該采取什么樣的跨越策略？教學(xué)實踐證明，“回歸教學(xué)原點”是預(yù)防思維定勢最有效的策略.這里的教學(xué)原點，一方面是指試題涉及的概念、公式、定理、基本數(shù)學(xué)思想方法等核心知識；另一方面是指試題的題型和試題求解過程中涉及的數(shù)據(jù)、結(jié)構(gòu)、待求待證以及由已知得到的推論等[1].

2 教學(xué)實踐

2.1直觀猜想 定義證明

解析法是解決解析幾何問題的通法，教學(xué)中教師往往也會忽視對圖形幾何特征的挖掘，都習(xí)慣用代數(shù)運算取代幾何證明，時間久了學(xué)生很容易產(chǎn)生思維定勢—幾何問題代數(shù)化，導(dǎo)致簡單問題復(fù)雜化解不出結(jié)果，沒有真正領(lǐng)悟解析幾何的本質(zhì)是幾何問題，近幾年的高考命題明顯加強在與平面幾何知識交匯處命制試題，解答此類試題圖形的幾何性質(zhì)往往能起到一錘定音的作用.

圖1

圖2

評注：方法一就是忽視解析幾何“形”的特征，受思維定勢的影響直接把點看成是直線與曲線的交點而代數(shù)化，雖然運算過程不算復(fù)雜，學(xué)生經(jīng)過運算也能得出正確結(jié)果，但要耗費不少時間，說明學(xué)生沒有真正弄清楚命題者的意圖：考察學(xué)生讀題、審題，通過直觀觀察產(chǎn)生猜想DF1//BF2，引發(fā)學(xué)生從平面幾何的角度去觀察圖形，利用點在曲線上的幾何意義去證明線線平行，從而達到以證代算的目的.

2.2 多元表征 合理轉(zhuǎn)化

求直線與橢圓交點坐標主要有兩種化歸的路徑：一是轉(zhuǎn)化成平面幾何問題來求解，二是通過聯(lián)立方程組來運算求解.化歸方式的不同，產(chǎn)生的分析問題與解決問題的思路就不同，運算的繁雜程度就會差異很大，所以采取對問題條件進行多元表征，合理選擇轉(zhuǎn)化路徑，有助于克服思維定勢提升學(xué)生分析問題、解決問題的能力.

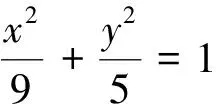
解析：如圖3，設(shè)線段PF的中點為M，橢圓的右焦點為F1.

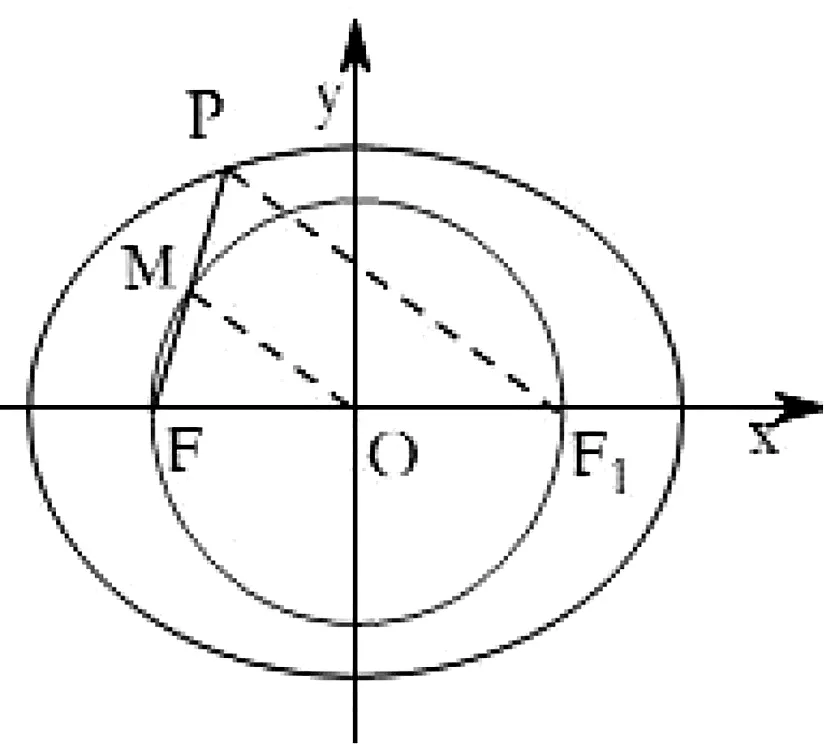
圖3

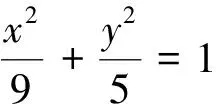
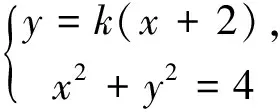
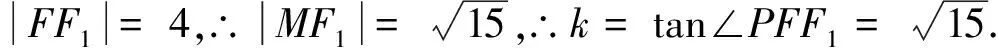
圖4

評注：本題通過感知(點、線、橢圓、圓)操作(輔助線)，可得點P(x0,y0)在橢圓上這個條件可以有以下三種等價轉(zhuǎn)化路徑：(1)P點滿足橢圓定義|PF1|+|PF|=2a；(2)P點滿足統(tǒng)一定義|PF1|=a+ex0；(3)P點是兩條曲線的交點.法1、法2運用解析法把P點看成是兩條曲線的交點，通過聯(lián)立方程組求點P的坐標，再用代數(shù)運算求直線斜率，思路簡單，學(xué)生也容易想到但運算量偏大.而法3、法4借助輔助線，利用橢圓定義和圓的幾何性質(zhì)就起到四兩撥千斤的效果.

3 結(jié)語

用幾何法求解解析幾何問題的優(yōu)點是簡潔、運算量小，但需要高層次的思維活動才能完成，學(xué)生沒有養(yǎng)成先形后數(shù)的思維順序分析問題的習(xí)慣與教師偏重用代數(shù)法解決解析幾何問題有關(guān)系，因此突破學(xué)生思維定勢困境的有效策略就是在教學(xué)過程中要改變注重解析法，忽視幾何法的不良習(xí)慣，回歸圓錐曲線的定義，以幾何圖形的幾何性質(zhì)作為切入點，探索解題的最佳路徑，優(yōu)化運算過程，提高學(xué)生的直觀想象、數(shù)學(xué)運算等核心素養(yǎng).