幾道上海高考數(shù)學填空壓軸題賞析

江西師范大學數(shù)學與統(tǒng)計學院 (330022) 汪美樂

《普通高中數(shù)學課程標準(2017)》指出：高中數(shù)學課程目標是發(fā)展學生的數(shù)學核心素養(yǎng)，即在學習數(shù)學和應用數(shù)學的過程中，發(fā)展學生數(shù)學抽象、邏輯推理、數(shù)學建模、直觀想象、數(shù)學運算、數(shù)據(jù)分析等數(shù)學學科核心素養(yǎng).《中國高考評價體系》強調(diào)高考評價由“一核”“四層”“四翼”組成，其中“四層”為“核心價值、學科素養(yǎng)、關鍵能力、必備知識”的考查內(nèi)容.隨著教育改革的深入，聚焦核心素養(yǎng)是教育發(fā)展的必然趨勢.高考數(shù)學如何更好地考查學生的數(shù)學核心素養(yǎng)，一直是數(shù)學教育研究的重要課題.本文擷取近年上海高考數(shù)學中的幾道填空壓軸題，就試題中體現(xiàn)的數(shù)學核心素養(yǎng)進行賞析.

圖1

賞析：本題的求解融合了“函數(shù)圖像與性質(zhì)”、“函數(shù)與方程”、“直線與曲線的位置關系”、“分段函數(shù)”等眾多知識，綜合性較強，突出了用平面解析幾何的方法解決數(shù)學問題的考查目標，要求學生具有一定的分析問題和解決問題的能力，并應具有較強的數(shù)學運算能力.解答過程應用了“數(shù)形結合”、“轉(zhuǎn)化與化歸”等數(shù)學思想方法，較好地聚焦了“數(shù)學運算”、“直觀想象”、“邏輯推理”等數(shù)學核心素養(yǎng)的考查.

圖2

賞析：本題以平面向量知識為載體，考查學生能將題中的代數(shù)語言轉(zhuǎn)化為圖形語言，并要求能將與圓的定義聯(lián)系起來，進而將題目條件轉(zhuǎn)化為圓與圓之間交點的個數(shù)情況.因此，解題的關鍵在于學生能夠有意識的將數(shù)與形結合以此來分析問題.故本題對數(shù)形結合的思想方法及對基礎知識的綜合運用要求較高，同時也考查到學生的邏輯推理、直觀想象、數(shù)學運算等核心素養(yǎng).

例3(2017年上海卷12題)如圖3，用35個單位正方形拼成一個矩形，點P1、P2、P3、P4以及四個標記為“▲”的點在正方形的頂點處，設集合Ω={P1，P2，P3，P4}，點P∈Ω，過P作直線lp，使得不在lp上的“▲”的點分布在lp的兩側.用D1(lp)和D2(lp)分別表示lp一側和另一側的“▲”的點到lp的距離之和.若過P的直線lp中有且只有一條滿足D1(lp)=D2(lp)，則Ω中所有這樣的P為.

圖3

圖4

賞析：本題以點與線的位置關系為背景，同時數(shù)學符號較多，題目較長，加大解題的難度，實際上，本題主要考查學生數(shù)學理解的能力及數(shù)學語言的轉(zhuǎn)化能力，充分考查學生的數(shù)學理性思維.求解的關鍵在于將題目轉(zhuǎn)化為平面直角坐標系中的四邊形.同時，求解中對學生數(shù)學抽象、邏輯推理及直觀想象素養(yǎng)要求也較高.

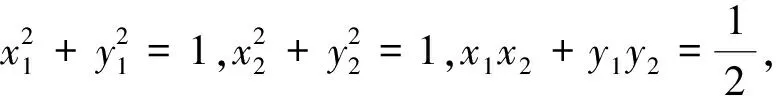
圖5

賞析：本題考查到圓、向量的數(shù)量積、點到直線的距離等相關知識的掌握程度，要求學生應熟悉掌握這些知識點，并能以形定數(shù)，再以形助數(shù)，運用數(shù)形結合的思想方法.解題的關鍵在于借助梯形中位線定理轉(zhuǎn)化為求中點到直線的距離最大值問題，運用到轉(zhuǎn)化與化歸思想.進一步凸顯數(shù)學抽象、直觀想象等核心素養(yǎng).

綜上可見，近年上海高考數(shù)學卷中的這幾道填空壓軸題對學生的核心素養(yǎng)進行較好的考查，有利于數(shù)學核心素養(yǎng)的發(fā)展.由此啟示我們應注重過程教學，在過程中理解數(shù)學知識，夯實基礎知識；加強思維能力的訓練，注重通性通法，發(fā)展數(shù)學思維，提高數(shù)學閱讀能力及問題轉(zhuǎn)化能力；重視數(shù)學語言，加強數(shù)學不同語言的表征；加強數(shù)學理解，掌握數(shù)學思想方法.只有這樣，才能真正將提升學生的數(shù)學核心素養(yǎng)落到實處.