異質網絡社區發現方法研究綜述

周萬珍 宋健 許云峰

摘 要：社區結構是復雜網絡研究中的重要領域，也是復雜網絡的重要特征之一，發現網絡中的社區結構在理解網絡功能方面起著重要作用。通過對國內外異質網絡社區發現文獻進行深入研究，較為全面地對現有異質網絡社區發現算法進行了歸納總結。首先，通過對國內外異質網絡社區發現文獻進行歸納，給出異質網絡社區發現的基本概述，明確異質網絡社區發現領域相關問題的基本定義。其次，介紹了異質網絡社區發現算法及主要評價指標，利用不同網絡結構以及算法對現有方法進行分類概述。最后，對異質網絡社區發現算法的發展趨勢進行了總結與展望，提出未來可以將研究重點集中在以下幾個方面：1）探索基于異質網絡的社區發現評價標準，以推動該領域的快速發展;2）設計更加通用的算法模型，解決由先驗知識引起的未知社區數量問題;3）開展更多關于動態網絡的研究。

關鍵詞：計算機神經網絡;復雜網絡;社區發現;異質網絡;圖神經網絡

中圖分類號：TP311.13 文獻標識碼：A

doi：10.7535/hbkd.2021yx03004

Survey of community discovery method of heterogeneous network

ZHOU Wanzhen， SONG Jian， XU Yunfeng

（School of Information Science and Engineering，Hebei University of Science and Technology，Shijiazhuang，Hebei 050018，China）

Abstract：Community structure is an important field in the research of complex networks，and it is also one of the important characteristics of complex networks.It is found that the community structure in the network plays an important role in understanding network functions.Through in-depth research on the literature of heterogeneous network community discovery at home and abroad，a more comprehensive summary of the existing heterogeneous network community discovery algorithm is carried out.Firstly，by summarizing the literature of heterogeneous network community discovery at home and abroad，the basic overview of heterogeneous network community discovery is given，and the basic definition of related issues in the field of heterogeneous network community discovery is defined.Then，it introduces the heterogeneous network community discovery algorithm and the main evaluation index，and classifies the existing methods by using different network structures and algorithms.Finally，the development trend of heterogeneous network community discovery algorithms is summarized and prospected，and the future research focus can be focused on the following aspects：1） Exploring the evaluation criteria of community discovery based on heterogeneous networks to promote the rapid development of this field Development;2） Design a more general algorithm model to solve the problem of the number of unknown communities caused by prior knowledge;3） Carry out more research on dynamic networks.

Keywords：

computer neural network;complex network;community discovery;heterogeneous network;graph neural network

現實世界中實體與實體之間的聯系都可以被表示為復雜網絡，比如人與人之間形成的社交網絡、作者之間形成的引文網絡、生物醫學領域的蛋白質相互作用網絡、化學分子網絡等。對于復雜網絡，錢學森先生給出了嚴格定義，將具有自組織、自相似、吸引子、小世界[1]、無標度特性[2]的網絡稱為復雜網絡。

研究復雜網絡的性質有助于人們對其加深理解和認識。例如，研究復雜網絡中的路徑長度、節點密度、節點的連通性等結構信息，有助于了解實體之間的關聯性質;研究復雜網絡中實體的屬性信息，有助于了解實體的固有性質。社區結構是復雜網絡中的另一個重要性質，從連通性和節點密度的角度出發，社區被稱為節點的局部密集連通子圖或聚類[3]。簡單而普遍的理解是，社區由2個規則組成，一是社區中的節點緊密相連，二是不同社區的節點稀疏連接[3]。現實世界中，同一個社區中的節點可以共享公共屬性或起類似的作用，這些共性幾乎是所有社區發現策略的關鍵。社區發現，或者更特別的說法——基于相似特征或者特征集的聚類，可以幫助人們理解復雜網絡的固有屬性和功能。例如，在蛋白質-蛋白質相互作用（PPI）網絡中的社區發現，揭示了具有相似功能的蛋白質[4];在Twitter和微博等社交網絡中，具有共同興趣的用戶或者共同朋友的用戶更有可能是同一個社區的成員[5];在引文網絡中，社區發現可以確定研究主題的重要性和發展方向[6]。

根據結構，復雜網絡可以分為同質網絡和異質網絡。早期，社區發現的相關研究多集中于同質網絡，有許多不錯的算法被提出。例如：2002年，GIRVAN等[3]提出了具有開創性的GN算法;2004年，NEWMAN等[7]提出了基于模塊度優化的FastGN算法，CLAUSET等[8]提出了CNM算法;2007年，RAGHAVAN等[9]提出了LPA算法;2008年，ROSVALL等[10]提出了Infomap算法，BLONDEL等[11]提出了Louvain算法;2016年，XU等[12]提出了基于骨干度的重疊社區發現算法等。

異質網絡具有高維度、多節點等特點，傳統的同質網絡社區發現方法無法應用于異質網絡，使得異質網絡社區發現研究成為一個新的挑戰。作為一個逐漸興起的研究領域，異質網絡社區發現仍處于探索階段，目前的研究方法還不是很成熟。現有的異質網絡社區發現方法可以分為傳統異質網絡社區發現方法和基于深度學習的異質網絡聚類方法2種。傳統的異質網絡社區發現方法大多針對特定網絡結構，不能對一般拓撲結構的大規模異質網絡進行社區發現。基于深度學習的異質網絡聚類方法大多先采用網絡表示學習方法對節點進行表示，然后進行特定的聚類任務。

目前，已有許多學者針對同質網絡社區發現發表了一些綜述性文獻[13-14]，但關于異質網絡社區發現的綜述較少。本文整理了當前比較熱門的傳統異質網絡社區發現方法和新興的基于深度學習的異質網絡聚類方法，根據算法的適用性及原理對現有方法進行歸納總結，并對異質網絡社區發現的未來進行展望。

1 異質網絡社區概述

1.1 信息網絡

信息網絡[15]（information networks）由有向圖G=V，E所定義，V表示節點集，E表示邊集，該有向圖中包含對象類型映射函數τ：V→A和連接類型映射函數φ：E→R，其中每一個對象v∈V都屬于一個特定的對象類型τv∈A，每一個連接e∈E都屬于一個特定的關系類型φe∈R。當節點類型數量為1，即∣A∣=1，同時，邊的類型數量也為1，即∣R∣=1時，稱這個信息網絡為同質網絡。反之，

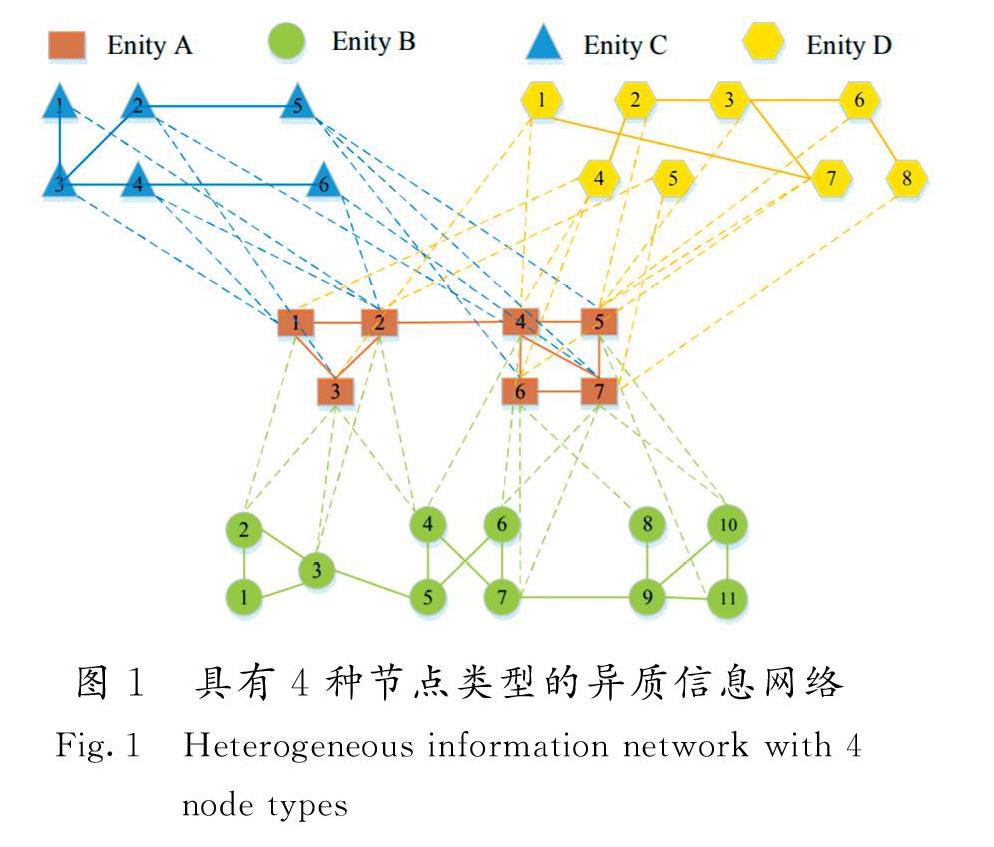
當節點的類型數量大于1，即∣A∣>1，或者，邊的類型數量大于1，即∣R∣>1時，則稱這個信息網絡為異質信息網絡[16]（以下簡稱異質網絡）。具有4種節點類型的異質信息網絡如圖1所示[17]。

異質網絡中也存在特殊情況，如多路網絡（multiplex networks）、多模網絡（multi-mode network）和多維度網絡（multi-dimensional network）。其中：多路網絡即節點類型為1、而關系類型為N的特殊異質網絡，通常是針對異構網絡中某種指定類型的中心節點而言的;多模網絡則側重于節點，指網絡中存在不同類型的節點;多維網絡側重于邊，指網絡中存在的不同關系類型的邊。

通常信息網絡中使用元路徑[15]（meta path）對網絡中不同的路徑進行定義。元路徑Φ是定義在模式S=A，R上的一條路徑，以A1→R1A2→R2…→RlAl+1的形式表示，其中R=R1R2…Rl是定義在對象A1，A2，…，Al+1中的一種復合關系，表示關系上的組合運算符。

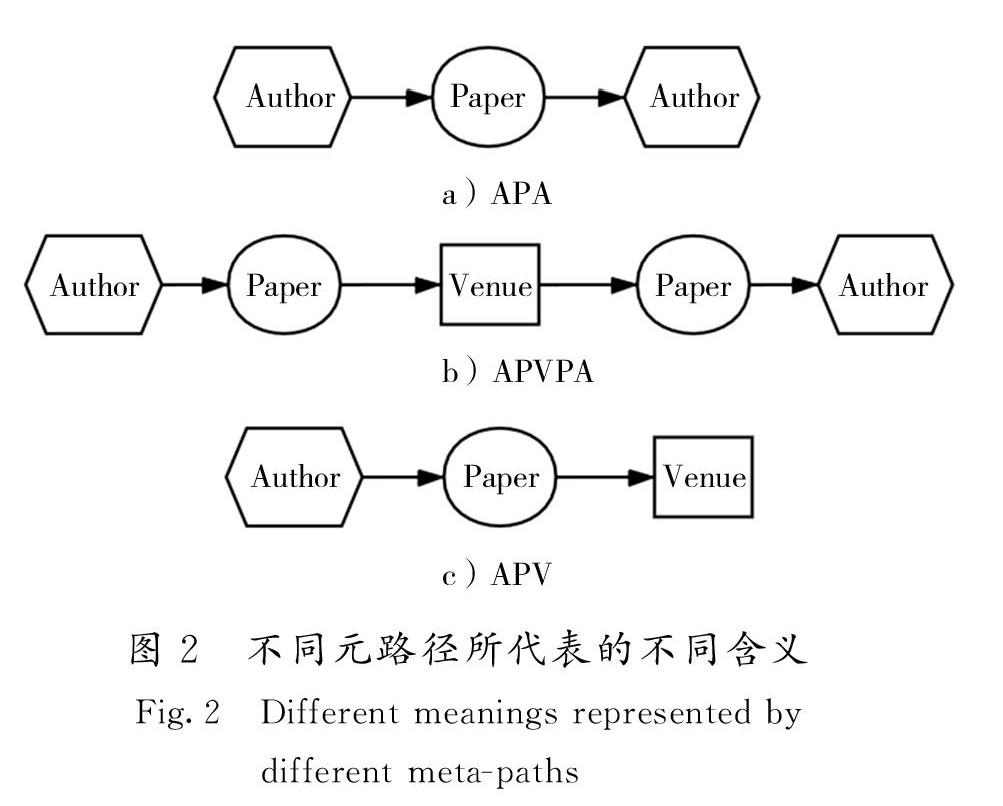
不同的元路徑可以表達異質網絡中不同的語義信息，根據這些語義信息可以將網絡劃分為不同的社區結構。圖2中，“Author”既可以由元路徑 “Author-Paper-Author”（APA）連接，也可以由元路徑“Author-Paper-Venue-Paper-Author”（APVPA）連接[18]。不同的元路徑所包含的語義信息是完全不同的，比如元路徑APA表示2位作者共同合作完成一篇文章，而元路徑APVPA則表示2位作者在同一機構完成不同的文章。

1.2 社區

所謂社區[13，19]，從連通性和密度的角度來看，社區被稱為節點的局部連通子圖或聚類，社區中的節點通常有著同樣的特征或起著相同的作用。根據圖論[20]，社區也被定義為集團（每個節點彼此相鄰）或連接的組件（每對節點至少通過一條路徑連接）。圖3示出了Zachary空手道俱樂部網絡，其中，不同顏色的符號表示在俱樂部的講師（節點1）和總裁（節點34）之間存在分歧之后產生的2個社區[14]。

1.3 社區發現

社區發現（也被稱為圖聚類技術）是基于網絡拓撲結構信息識別出的具有相似特征或起相同作用的節點的集合。在過去幾十年中，社區發現受到了學者們的廣泛關注，并取得了很多開創性的研究成果。例如：2002年，GIRVAN等[3]提出了GN算法，

掀起了社區發現的研究熱潮，引起了計算機、物理、生物等眾多學科領域的關注;2004年，NEWMAN[21]提出了模塊度Q函數作為社區發現的評價指標，推動了社區發現領域的相關研究快速向前發展。但是，以上研究是基于非重疊社區結構的，即一個節點只屬于一個社區（見圖4a））。而在現實生活中，更為常見的是重疊社區結構（見圖4b）），即一個節點屬于多個社區。例如：生物信息學科學者發表的文章通常涉及生物以及信息2個領域;一名鐵人三項運動員既屬于跑步俱樂部，又屬于自行車俱樂部。

相比于同質網絡，現實生活中更為常見的是異質網絡，即多類型節點和多類型關系組成的網絡。異質網絡不僅包括多種節點類型，還包括各種不同節點類型之間的復雜關系。例如：引文網絡中的作者、論文、作者單位等節點之間的關系，作者與論文之間是寫作關系，作者與作者之間是合作關系，作者與作者單位之間是隸屬關系，論文與論文之間是引用關系等。異質網絡中的社區結構一般被定義為同種類型節點組成的社區，社區間形成多對多關系[22]。

由于異質網絡的復雜性，導致僅有結構最為簡單的二分網絡得到了一定的研究。二分網絡僅由2種節點類型組成，不同類型的節點之間有較多的邊連接，而同類型之間大多沒有邊。由于異質網絡具有多分多維的特性，因而二分網絡有2種形式的社區結構定義。第1種是基于同質網絡的社區定義，將不同類型的節點劃分到同一個社區，社區內不同類型節點間緊密連接，社區間形成一對一關系，如圖5a）所示;第2種是基于社區內相似節點聚類來考慮的，將二分網絡中同類型節點劃分到一個社區，社區內的節點間沒有連接，異質社區間形成多對多關系，如圖5b）所示[22]。

1.4 社區發現的實際應用

社區發現可以被應用到許多任務中，寬泛地分為2類：鏈路預測和社交影響力最大化。

1.4.1 鏈路預測

鏈路預測是數據挖掘領域的重要研究方向，是指通過已知節點的特征信息以及網絡拓撲結構，預測尚未產生連接的節點對之間出現連邊的可能性[23]。鏈路預測可以識別具有相似購買歷史的用戶組，進行更加有效的推薦。

1.4.2 社交影響力最大化

影響力最大化的應用場景十分豐富，包括病毒營銷、信息擴散、推薦系統等。影響力最大化的目的是在特定的網絡傳播模型下找到一組節點，使得這組節點的最終影響力達到最大化。在社交網絡中，由于社區結構的特性，社區內部節點通常具有相似的特征，因此信息在社區內部的傳播速度較快。因此，一些科研人員嘗試將社區發現與影響力最大化進行研究，取得了不錯的效果。

2 異質網絡社區發現方法

研究人員對同質網絡提出了許多優秀的社區發現算法，例如譜方法[24]和標簽傳播方法[25]。但是這些算法并沒有考慮網絡的異質性，檢測到的社區僅僅反映連接密度關系，無法反映異質網絡中不同連接類型之間的語義關系。早期，受限于異質網絡的復雜性與計算機的計算能力，傳統異質網絡社區發現方法多集中于結構較為簡單的二分網絡和多分多維網絡。隨著計算能力的提高以及深度學習的興起，基于深度學習的異質網絡聚類方法逐漸成為研究的主要方向。

2.1 傳統異質網絡社區發現方法

2.1.1 二分網絡的異質網絡社區發現方法

目前，二分網絡社區發現主要有2種方法：一是將二分網絡投影降維為同質網絡，再使用同質網絡社區發現算法對其進行社區劃分，但該方法在投影降維過程中容易造成部分信息丟失;二是直接在二分網絡上進行社區劃分。

2007年，BARBER[26]開創性地提出了二分模塊度，并基于此提出了一種基于二分模塊度的Brim算法，克服了同質網絡模塊度在異質網絡中效果不佳的缺陷，但該方法無法有效識別出網絡中的小規模社區。針對這一問題，XU等[27]提出了基于密度的二分網絡模塊度，從網絡連接密度出發，同時考慮二分網絡社區內連接數量和節點數量，提升對小規模社區的識別效果。

2.1.2 多分多維的異質網絡社區發現方法

2009年，SUN等[28-29]提出了基于概率模型的RankClus算法以及NetClus算法，采用排名和社區發現相互提升的思路，將排名問題和社區發現問題結合在一起。通過迭代“根據當前社區劃分計算節點的等級分布”和“計算節點所屬社區的后驗概率，以及當前等級分布調整節點的社區劃分”來進行社區發現，直到收斂為止。但這2種方法均是針對某一特定的網絡結構類型提出的，RankClus針對的是雙類型異質網絡，NetClus針對的是包含多種實體類型的異構星形網絡。為了解決這一問題，MING等[30]提出了RankClass算法，該算法在NetClus的基礎上進行改進，使其可以應用于具有常規拓撲結構的異質網絡。具體地說，RankClass通過建立一個基于圖的排名模型，根據排名結果對網絡結構進行調整，使得排名高的對象組成的子網絡的重要性得以加強，最后通過估計各個對象屬于每個類的后驗概率來確定每個對象的最佳類別。QIU等[31]注意到上述方法未考慮重疊社區問題，因此提出了OcdRank算法，該算法在有向異質的社交網絡中將重疊社區發現和社區成員排名結合在一起，通過區分不同類型的節點來改善RankClus，同時該方法支持增量更新的社區發現，這在現實場景中具有很大的應用價值。以上基于概率模型的異質網絡社區發現算法具有較高的時間和空間復雜度，且由于需要豐富的先驗知識以及預先設定社區數量，導致在大規模異質網絡中社區發現的效果并不佳。

2011年，COMAR等[32]提出了基于非負矩陣分解的社區發現算法，使用鄰接矩陣表示異質網絡，通過將鄰接矩陣分解成潛在因子進行社區發現。但是該算法只能用于A=2，R=3的異質網絡。針對上述算法只能用于特定網絡結構這一問題，LI等[33]提出了一個基于正則化和非負矩陣分解（regularized joint nonnegative matrix factorization，簡稱RJNMF）的框架，該框架在構建異質網絡鄰接矩陣時綜合考慮鏈路信息和節點內容信息，引入調節功能以減少噪聲數據對社區的影響，以此提高社區發現的效果。CHEN等[34]將同質網絡中基于矩陣分解的社區發現算法Hom-SC和Hom-RSC擴展至異質信息網絡中，分別命名為Het-SC和Het-RSC。具體地說，通過對給定圖的拉普拉斯矩陣進行矩陣分解獲得其特征向量，然后對不同節點類型對應的特征向量進行K-means聚類，獲得社區劃分結果。基于矩陣分解的算法可以有效識別異質網絡的異質性，但是針對大規模網絡進行矩陣分解具有較高的時間、空間復雜度，同時由于需要在進行社區劃分之前對社區數量進行設定，因此對先驗知識要求較高。

2016年，LIU等[35]提出了以種子為中心的社區發現算法DenSeC，該算法根據節點密度對中心節點進行識別，然后將中心節點從緊密連接區域擴展到稀疏連接區域，并不斷吸收新節點生成最終的社區劃分。2018年，LU等[17]提出了用于多維社區發現的Hete_MESE算法，該算法可以從多維度檢測異質網絡中的重疊和異質社區，具有線性時間復雜度，因此可以應用于大規模異質網絡。具體來說，首先將異質網絡中的多個實體類型之一指定為社區中心節點類型，基于中心節點以及元路徑提取多路網絡，然后基于多路網絡檢測重疊的社區，并將其視為種子社區，吸收其他實體類型生成異質社區。

基于以上研究可以發現，傳統異質網絡社區發現方法遵循由特殊網絡結構到一般拓撲結構、由非重疊社區發現到重疊社區發現這一發展路線;同時可以發現，隨著網絡規模的增大，傳統算法近年的研究目標主要集中于如何降低時間、空間復雜度以及減少對先驗知識的依賴方面。

2.2 基于深度學習的異質網絡聚類方法

近年來，基于深度學習的網絡表示學習方法是數據挖掘領域研究的熱門方向[36]，該方法可以將信息網絡表示為低維稠密的攜帶網絡節點特征信息的實數向量，并應用于下游任務的輸入，如聚類、社區發現等。TOMMASEL等[37]的研究表明，僅關注網絡拓撲結構的傳統方法忽略了節點間的語義信息，而深度學習技術可以同時考慮網絡拓撲結構與網絡上的語義信息。已有研究表明，深度學習技術可以提高社區發現的準確性[38]。例如，CHEN等[39]提出的線圖神經網絡模型（line graph neural network，簡稱LGNN），通過基于深度學習的聚類方法解決社區發現問題，取得了較為顯著的效果。由此可見，基于深度學習的聚類方法可以幫助研究人員進行社區發現。

由于異質網絡多節點類型、關系類型的特性，異質圖神經網絡通常會采用層次聚合的方式獲得節點的表示信息：1）節點級別，獲得節點在某種關系（即某條元路徑）下的鄰居節點并聚合鄰居節點信息，獲得節點在該關系下的表示;2）語義級別，對多種關系（即不同元路徑）下的節點表示進行融合，獲得最終的節點表示。

異質網絡表示學習中，首先要解決的問題是不同節點類型以及不同關系類型對節點表示的影響。為解決此問題，WANG等[40]提出了基于注意力機制的異質圖神經網絡（heterogeneous graph attention network，簡稱HAN）。HAN采用經典的層次聚合方式對節點進行全面表示，通過設置節點級別注意力和語義級別注意力，判斷不同鄰居節點與元路徑的重要性，最后通過相應的聚合操作對鄰居節點的信息以及不同元路徑的信息進行聚合以獲得最終的節點表示。

HAN中節點級別的信息聚合如下：

eΦij=attnodeh′i，h′j;Φ，

zΦi=σ∑j∈NΦiαΦijh′j。

式中：eΦij代表節點i在元路徑Φ下鄰居節點j的權重;zΦi即節點i在元路徑Φ下的節點級別的表示。每個節點由多條元路徑構成，給定一組元路徑Φ0，Φ1，…，ΦP，可以得到一組節點級別的節點表示ZΦ0，ZΦ1，…，ZΦP。

HAN中語義級別的信息聚合如下：

βΦ0，βΦ1，…，βΦP=attsemZΦ0，ZΦ1，…，ZΦP，

Z=∑Pi=1βΦiZΦi。

式中：βΦ0，βΦ1，…，βΦP代表各條元路徑的權重;Z為最終的節點表示。由于每個節點的最終表示Z融合了多條元路徑及不同鄰居節點信息，因此HAN可以為每個節點都獲得更為全面的表示。

與HAN不同，ZHANG等[41]提出的HetGNN（heterogeneous graph neural network）則是在節點級別的信息聚合中使用LSTM作為聚合器，對某種關系下的鄰居節點信息進行聚合以獲得節點的表示，在語義級別的信息聚合中，使用注意力機制獲得最終的節點表示。

HetGNN中，節點級別的信息聚合如下：

ft2v=∑v′∈NtvLSTMf1v′LSTMf1v′Ntv。

式中：Ntv是節點v在特定關系t下（即某條元路徑）的鄰居節點的集合;f1v′是鄰居節點v′的初始節點表示;ft2v為節點v在節點級別的表示。

HetGNN中語義級別的信息聚合如下：

εv=αv，vf1v+∑t∈OVαv，tft2v。

式中：εv為聚合了多條元路徑的節點v的最終表示;αv，v表示節點對自身信息的權重;αv，t表示節點v在特定關系t下的節點表示的權重;OV表示節點類型的集合。

以上2種適用于聚類任務的異質圖神經網絡雖然取得了不錯的效果，但仍然存在一些缺陷，比如需要預先指定元路徑，元路徑的選擇將直接影響到模型的效果，而元路徑的選擇又需要豐富的先驗知識。這一缺陷極大影響了相關任務的效果。為解決這一問題，YUN等[42]提出了自適應選取元路徑的GTN（graph transformer networks）模型，該方法從原始圖結構中抽取2個圖結構，通過矩陣乘法生成元路徑，并通過多通道卷積學習不同類型的元路徑，然后將GCN應用于每個通道對多個節點表示進行拼接，作為最終的節點表示。該方法雖然顯著提升了節點分類任務的性能，但在聚類任務中表現并不佳。FU等[43]提出的MAGNN模型首先是將特定類型的線性變換應用于異構節點屬性，將不同類型的節點屬性投影到相同的潛在向量空間，以此解決節點屬性的異構性;然后，對于節點級別的信息聚合采用特殊的元路徑實例編碼器，將節點特征編碼為向量，對于語義級別的消息則使用注意力機制進行聚合。

基于以上研究可知，異質圖神經網絡聚類方法的研究重點主要包括以下幾方面：節點級別、語義級別信息聚合方式的選擇，不同類型的節點屬性處理方式，元路徑的選擇方式。異質圖神經網絡能夠同時學習網絡結構特征以及節點屬性特征，顯著提高了聚類任務的效果。同時，異質圖神經網絡適用于任意網絡結構的特性也為后續的社區發現任務提供了極大便利。相比于傳統社區發現算法，異質圖神經網絡模型的數據適應性更強，更能有效利用數據的特征。

2.3 方法總結與歸納

根據算法特點及適用的網絡結構對上述算法進行了整理，詳見表1。

3 異質網絡社區發現的評價指標及常用數據集

3.1 異質網絡社區的模塊度

2004年，NEWMAN等[7]創造性地提出了模塊度Q函數，自此模塊度Q成為衡量社區劃分質量優劣的一個重要評價指標，現已成為常用的評價指標之一。該指標主要面向無向無權的同質網絡，網絡中不同的社區劃分結果對應不同的模塊度Q，模塊度Q越大，則社區劃分結果越好，相反則越差。相比之下，由于異質網絡的復雜性，目前僅有部分學者針對二分網絡提出了相應的模塊度。

2007年，BARBER[26]率先提出了基于二分網絡的模塊度，將不同類型的節點劃分到同一個社區中，計算方法如下：

Qb=1M∑ni=1∑mj=1Ai，j-titjmδCi，Cj。

式中：m表示網絡中的邊數;Ai，j表示鄰接矩陣A中的元素，若節點相連，則Ai，j=1，否則Ai，j=0;Ci與Cj分別表示節點i與節點j所屬的社區，若節點i與節點j所屬的社區相同，則δCi，Cj=1，反之則為0。

2010年，LIU等[44]提出了一對多關系的二分模塊度，用于表示2個社區對應關系的強弱度，計算方法如下：

Qm=∑lQml=1M∑i=1etm-alam。

式中：l，m分別對應2個異質網絡社區;Q值越大，表示二分網絡的結構越強。

3.2 通用評價指標

標準化互信息（normalized mutual information，簡稱NMI）[45]，是目前廣泛使用的一種社區劃分評價指標。計算方法如下：

NMIR，F=-2∑CRi=1∑CFj=1NijlogNijSNi*N*j∑CRNi*logNi*/S+∑N*jlogN*j/S。

式中：給定一個矩陣N，N表示由真實社區與社區發現算法計算出來的社區對應的混合矩陣，Ni*表示真實的社區，N*j表示社區發現算法所得到的社區;Nij表示同時出現在真實社區與社區算法所得社區中的節點數量;S表示所有元素之和;CR表示真實社區的數量;CF表示算法所得到的社區數量。當算法所得的社區劃分與真實社區完全一致時，NMI=1;當算法所得的社區劃分與真實社區相互獨立時，NMI=0。顯然，NMI值越大，社區發現算法效果越好。

3.3 異質網絡社區發現的常用數據集

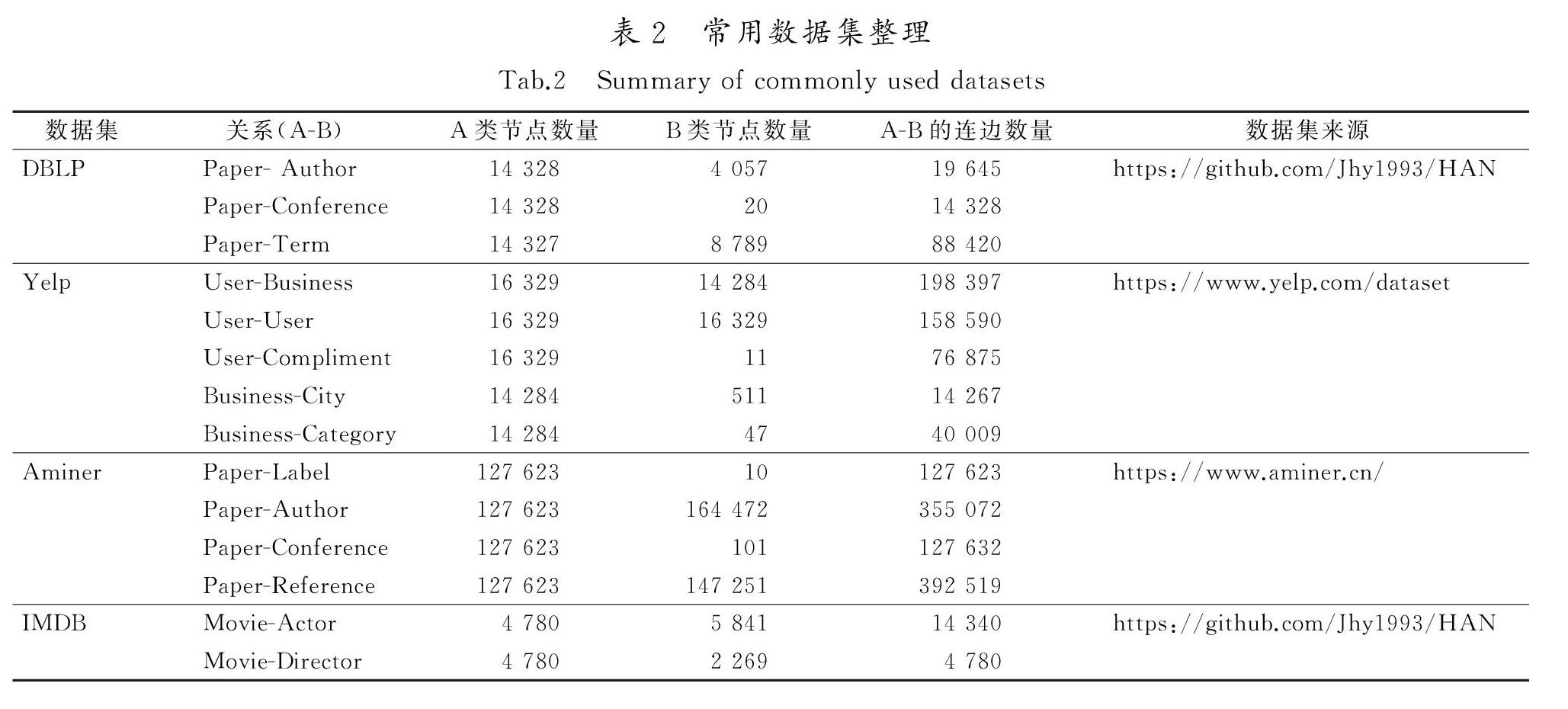
表2給出了4種常用測試算法效果的異質網絡數據集，分別為引用網絡DBLP、美國最大的點評網站Yelp數據集、大數據挖掘與服務系統平臺Aminer、電影信息數據集IMDB。對于每個數據集，給出了數據來源，并統計了該數據集的節點數、關系數、關系類型，方便研究者選擇適合模型的數據集。

4 研究展望

本文介紹了現有的異質網絡社區發現方法，根據其特點及網絡結構可分為3類，分別是二分網絡社區發現方法、多模多維社區發現方法以及最近非常流行的基于深度學習的異質網絡聚類方法，對比了所介紹模型的適用性與算法特點，給出了經典的異質網絡數據集。

近年來，社區發現領域的研究發展迅速，但是在一些方面仍然存在挑戰。例如，由于數據類型的多樣性，不同領域的先驗知識極大影響了社區劃分的結果。因此，設計高效通用的社區發現算法非常重要。同時，在近兩年嶄露頭角的基于深度學習的圖神經網絡方法展現出了巨大潛力，預示著在今后的研究中，圖神經網絡方法可能成為解決現有問題的一種有效途徑。針對社區發現領域的研究現狀，未來研究重點將會集中在以下幾個方面。

1）評價標準

異質網絡社區發現算法仍然缺少統一的評價標準，尋找一個科學的評價標準將是研究人員面臨的第一個挑戰。根據異質網絡社區發現算法的發展趨勢，新的評價標準不僅需要考慮同種類型節點間的社區連接強度，還需要考慮不同類型節點間的社區連接強度。面對這一挑戰，同時考慮密度與節點擴張程度或許是一個新的方向。同時，面對不同的任務需求，異質網絡中的重疊社區發現也變得極為重要，因此如何評價異質網絡中的重疊社區劃分也是一項新挑戰。

2）未知的社區數量

由于從現實世界網絡中提取的大多數數據都沒有標簽，因此無法提前預知社區數量，這會影響到許多需要預先設定社區數量的算法效果。通常，社區數量的設定是由先驗知識決定的，因此社區發現算法可以通過減少對先驗知識的依賴解決這一難題，可以從節點屬性中學習得到與先驗知識相關的特征。盡管已經有部分研究者提出了解決方案，但是這個問題仍然沒有得到充分解決，有待進一步研究。

3）動態網絡

動態變化會影響網絡拓撲結構以及節點特征，使得每個特征都必須以不同的方式進行處理。拓撲變化，如添加或刪除邊，會引起社區變化以及整個網絡拓撲結構的變化。使用動態網絡模型通常要用一系列快照進行重新訓練，因此未來動態網絡時間屬性所面臨的技術挑戰在于對動態特征的提取。

4）節點的表示學習

隨著深度學習的發展，基于神經網絡的表示學習方法引起了復雜網絡研究者的關注，該方法可以將信息網絡表示為低維稠密的攜帶網絡節點特征信息的實數向量，并應用于下游任務的輸入。由于網絡表示學習擁有強大的建模能力，因此將其與社區發現任務相結合將是未來研究的一個新方向。

參考文獻/References：

[1] WATTS D J，STROGATZ S H.Collectivedynamics of 'small-world'networks[J].Nature，1998，393（6684）：440-442.

[2] BARABSI A L，ALBERT R.Emergence of scaling in random networks[J].Science，1999，286（5439）：509-512.

[3] GIRVAN M，NEWMAN M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences.2002，99（12）：7821-7826.

[4] CHEN J C，YUAN B.Detecting functional modules in the yeast protein-protein interaction network[J].Bioinformatics，2006，22（18）：2283-2290.

[5] YANG J，MCAULEY J J，LESKOVEC J.Community detection in networks with node attributes[C]//13th International Conference on Data Mining.[S.l.]：[s.n.]，2013：1151-1156.

[6] CHEN P，REDNER S.Community structure of the physical review citation network[J].Journal of Informetrics，2010，4（3）：278-290.

[7] NEWMAN M E J，GIRVAN M.Finding and evaluating community structure in networks[J].Physical Review E，2004，69（2）：1-16.

[8] CLAUSET A，NEWMAN M E J，MOORE C.Finding community structure in very largenetworks[J].Physical Review E，2004，70（6）：026132.

[9] RAGHAVAN U N，ALBERT R，KUMARA S.Near linear time algorithm to detect community structures in large-scale networks[J].Physical Review E，2007，76（3）：036106.

[10]ROSVALL M，BERGSTROM C T.Maps of random walks on complex networks reveal community structure[J].Proceedings of the National Academy of Sciences of the United States of America，2008，105（4）：1118-1123.

[11]BLONDEL V D，GUILLAUME J L，LAMBIOTTE R，et al.Fast unfolding of communities in largenetworks[J].Journal of Statistical Mechanics：Theory and Experiment，2008，2008（10）：10008.

[12]XU Y F，XU H，ZHANG D W.A novel disjoint community detection algorithm for social networks based on backbone degree and expansion[J].Expert Systems with Applications，2015，42（21）：8349-8360.

[13]FORTUNATO S.Community detection in graphs[J].Physics Reports，2010，486：75-104.

[14]FORTUNATO S，HRIC D.Community detection in networks：A user guide[J].Physics Reports，2016，659：1-44.

[15]SUN Y Z，HAN J W.Meta-path-based search and mining in heterogeneous information networks[J].Tsinghua Science and Technology，2013（4）：329-338.

[16]SUN Y Z，HAN J W.Mining heterogeneous information networks：A structural analysis approach[J].Acm Sigkdd Explorations Newsletter，2013，14（2）：20-28.

[17]LU M L，QU Z H，WANG Z H，et al.Hete_MESE：Multi-dimensional community detection algorithm based on multiplex network extraction and seed expansion for heterogeneous information networks[J].IEEE Access，2018，6：73965-73983.

[18]SHI C，YU P S.Heterogeneous Information Network Analysis and Applications[M].[S.l.]：Springer，2017.

[19]LIU F Z，XUE S，WU J，et al.Deep learning for community detection：progress，challenges and opportunities[C]// International Joint Conference onArtificial Intelligence.[S.l.]：[s.n.]，2020：4981-4987.

[20]MALLIAROS F D，VAZIRGIANNIS M.Clustering and community detection in directed networks：A survey[J].Physics Reports，2013，533：95-142.

[21]NEWMAN M E J.Fast algorithm for detecting community structure in networks[J].Physical Review E，2004，69：066133.

[22]趙衛績，張鳳斌，劉井蓮.復雜網絡社區發現研究進展[J].計算機科學，2020（2）：10-20.

ZHAO Weiji，ZHANG Fengbin，LIU Jinglian.Review on community detection in complex networks[J].Computer Science，2020（2）：10-20.

[23]GUIMERA R，SALES-PARDO M.Missing and spurious interactions and the reconstruction of complex networks[J].Proceedings of the National Academy of Sciences of the United States of America，2009，106（52）：22073-22078.

[24]CHENG J J，LI L J，LENG M W，et al.A divisive spectral method for network community detection[J].Journal of Statistical Mechanics Theory & Experiment，2016，2016（3）：033403.

[25]SUN H L，HUANG J B，TIAN Y Q，et al.Detecting overlapping communities in networks via dominant label propagation[J].Chinese Physics B，2015，24（1）：018703.

[26]BARBER M J.Modularity and community detection in bipartite networks[J].Physical Review E，2007，76（6）：066102.

[27]XU Y C，CHEN L，LI B，et al.Density-based modularity for evaluating community structure in bipartite networks[J].Information Sciences，2015，317：278-294.

[28]SUN Y Z，HAN J W，ZHAO P，et al.Rankclus：Integrating clustering with ranking for heterogeneous information network analysis[C]//International Conference on Extending Database Technology.[S.l.]：[s.n.]，2009：565-576.

[29]SUN Y Z，YU Y，HAN J W.Ranking-based clustering of heterogeneous information networks with star network schema[C]//Acm Sigkdd International Conference on Knowledge Discovery & Data Mining.[S.l.]：[s.n.]，2009：797-806.

[30]MING J，HAN J W，DANILEVSKY M.Ranking-based classification of heterogeneous information networks[C]//Acm Sigkdd International Conference on Knowledge Discovery & Data Mining.[S.l.]：[s.n.]，2011：1298-1306.

[31]QIU C H，WEI C，WANG T J，et al.Overlapping Community Detection in Directed Heterogeneous Social Network[M].[S.l.]：Springer International Publishing，2015：490-493.

[32]COMAR P，TAN PN，JAIN A K.A framework for joint community detection across multiple related networks[J].Neurocomputing，2012，76（1）：93-104.

[33]LI Z，PAN Z S，ZHANG Y Y，et al.Efficient community detection in heterogeneous social networks [J].Mathematical Problems in Engineering，2016（12）：1-15.

[34]CHEN Y G，SENGUPTA S.Spectral clustering in heterogeneous networks[J].Statistica Sinica，2015，25：1081-1106.

[35]LIU W，CHEN M，LIU K，et al.A Density-based seed-centric community detection algorithm[C]//IEEE Web Information Systems and Applications Conference.[S.l.]：[s.n.]，2017：149-154.

[36]魯軍豪，許云峰.信息網絡表示學習方法綜述[J].河北科技大學學報，2020，41（2）：133-147.

LU Junhao，XU Yunfeng.A survey of information network representation learning[J].Journal of Hebei University of Science and Technology，2020，41（2）：133-147.

[37]TOMMASEL A，GODOY D.Multi-view community detection with heterogeneous information from social media data[J].Neurocomputing，2018，289：195-219.

[38]CAI B，WANG Y，ZENG L，et al.Edge classification based on convolutional neural networks for community detection in complex network[J].Physica A：Statistical Mechanics and Its Applications，2020，556：124826.

[39]CHEN Z D，LI X，BRUNA J.Supervised community detection with line graph neural networks[C]//International Conference on Learning Representations.[S.l.]：[s.n.]，2019：1-15.

[40]WANG X，JI H Y，SHI C，et al.Heterogeneous graph attention network[C]//The World Wide Web Conference.[S.l.]：[s.n.]，2019：2022-2032.

[41]ZHANG C X，SONG D J，HUANG C，et al.Heterogeneous graph neural network[C]//Acm Sigkdd International Conference on Know-ledge Discovery & Data Mining.[S.l.]：[s.n.]，2019：793-803.

[42]YUN S，JEONG M，KIM R，et al.Graph transformernetworks[C]//Neural Information Processing Systems.[S.l.]：[s.n.]，2019：11960-11970.

[43]FU X Y，ZHANG J N，MENG Z Q，et al.MAGNN：Metapath aggregated graph neural network for heterogeneous graph embedding[C]// WWW20：The Web Conference 2020 Taipei Taiwan.[S.l.]：[s.n.]，2020：2331-2341.

[44]LIU X，MURATA T.Evaluating community structure in bipartite networks[C]//IEEE Second International Conference on Social Computing.[S.l.]：[s.n.]，2010：576-581.

[45]劉井蓮，王大玲，趙衛績，等.一種基于核心節點擴展的社區挖掘算法[J].山東大學學報（理學版），2016，51（1）：106-114.

LIU Jinglian，WANG Daling，ZHAO Weiji，et al.A community mining algorithm based on core nodes expansion[J].Journal of Shandong University（Natural Science），2016，51（1）：106-114.