基于復變函數的斜頂巷道圍巖應力分布解析解

賀 凱，常聚才，李萬峰，李世輝，李 冬

(1.安徽理工大學煤礦安全高效開采教育部重點實驗室，安徽 淮南 232001；2.淮河能源控股集團有限責任公司，安徽 淮南 232001)

在開采傾斜煤層時，回采巷道往往沿煤層頂板掘進，以達到不破壞巷道頂板的目的。因此，形成了應用廣泛的斜頂巷道。斜頂巷道圍巖的應力分布是其支護設計的重要依據，但是，由于斜頂巷道斷面的不規則性，其應力分布的求解是一個難題。前蘇聯科學家穆斯海里什維利提出的復變函數法可用于求解斜頂巷道圍巖應力分布的解析解[1]。國內外學者運用復變函數法對不同斷面巷道圍巖應力分布做了很多研究[1-14]。薩文[2]和陳子蔭[3]求解了各向異性彈性條件下橢圓形斷面巷道的應力分布解析解；施高萍等[4]分析了原巖垂直應力和水平應力對矩形巷道頂板和巷幫中點的應力集中系數分布的影響規律；陳凱等[5]采用復變函數解法對矩形巷道圍巖彈性應力分布進行了求解，獲得了基于曲線坐標系的應力張量解析解，分析了高寬比和側向壓力對圍巖應力分布的影響規律；侯化強等[6]通過復變函數法和彈塑性理論提出了矩形巷道圍巖具有塑性滑動區、裂隙擴展區及圍巖穩定區的“三區”理論；寧德義[7]結合復變函數法和鮑爾丁-湯姆遜黏彈性本構模型，得到深部矩形巷道圍巖的粘彈性應力分布；袁林等[8]結合復變函數和廣義開爾文模型推導出了矩形巷道周邊應力集中系數表達式，并分析了應力集中系數和時間的關系。其他關于不同斷面巷道圍巖應力分布的研究還如文獻[9-14]所示。現有文獻對橢圓形、矩形等規則斷面巷道圍巖應力分布研究較為充分，但是缺少針對斜頂巷道的相關研究。參考前人的研究成果，采用復變函數法求解斜頂巷道圍巖應力分布解析解，以淮南礦業集團潘三煤礦17102(3)運輸巷為工程背景，討論斜頂巷道圍巖主應力和主應力集中系數的分布規律。

1 斜頂巷道圍巖應力分布求解

深埋地下的斜頂巷道可以看成無限大平面的孔口問題，所受圍巖壓力用垂直壓力σV、水平壓力σH和剪應力τ表示，斜頂巷道受力模型如圖1所示。

圖1 斜頂巷道受力模型

斜頂巷道圍巖應力分布求解的具體步驟是：首先，將斜頂巷道外域通過共形映射函數映射到復平面上的單位圓內；其次，依據共形映射函數和邊界條件確定兩個表征應力分布的復位勢函數的基本形式；然后，根據邊界條件運用復分析的相關知識求解表征應力分布的復位勢函數；最后，由復位勢函數求得應力分布[1-3]。

1.1 共形映射函數

黎曼映射定理表明[15，16]，通過共形映射函數ω(ξ)可將實平面上的斜頂巷道圍巖區域映射到復平面上的單位圓內，如圖2所示。

圖2 共形映射

針對不規則斷面巷道，共形映射函數ω(ξ)無法使用有限初等函數項表示，將其展開為Laurent級數，并取有限項作為對共形映射函數ω(ξ)的近似：

式中，ξ=ρeiθ代表單位圓所在的復平面上點的坐標；An和Bn為實數，取值與巷道斷面形狀有關；N表示Laurent級數的階數。本文根據參考文獻[15，16]提出的算法，運用科學計算軟件編程，求解An和Bn。當N趨向無窮大時，共形映射函數在巷角處的曲率半徑趨近于0。因此，巷角處的曲率半徑可用于度量共形映射函數的精度，曲率半徑越小表明共形映射函數精度越高。曲率半徑公式為：

式中，θ0表示巷角對應的單位圓上點的極角。實平面上點的坐標與復平面上點的坐標之間的對應關系為：

式中，函數Re表示取復數的實部；函數Im表示取復數的虛部。將式(3)代入式(2)即可求得巷角的曲率半徑。

設點A在巷道斷面邊界上，點B在共形映射函數ω(ξ)的映射圖形上。當N趨向無窮大時，共形映射函數ω(ξ)的映射圖形與巷道邊界重合，此時如果點A與點B重合，則稱其為一對對應點。當點A和B表示任意一對對應點時，可定義共形映射函數的最大絕對誤差為：

式中，xA、xB、yA和yB表示點A和B的坐標；函數max()表示取最大值。

1.2 復位勢函數的求解

圍巖應力可由2個復位勢函數φ(z)和ψ(z)確定。針對斜頂巷道圍巖應力分布求解問題，復位勢函數形式為[1-3]：

式中，復變函數φ0(ξ)和ψ0(ξ)表示在定義域內滿足柯西-黎曼條件的解析函數，見式(6)；α取值與圍巖所受壓力有關，見式(7)。

式(6)中系數an和bn為復數。通過巷道表面的邊界條件可求得系數an和bn。依據Harnack定理[1，2]，可將巷道表面的邊界條件等效為兩個泛函方程：

式中，γ表示巷道邊界曲線；f0與巷道邊界條件有關，取值為：

將式(6)、(7)和(9)代入式(8)，并利用Cauchy積分公式，即可求得復系數an和bn，具體求解過程見參考文獻[1-3]。然后可通過式(10)求得圍巖應力分布。

由式(10)計算得到的應力分量是基于共形映射函數ω(ξ)確定的曲線坐標系[1]，需要將曲線坐標系中的應力分量變換到直角坐標系中。由微分幾何學可得曲線坐標系到直角坐標系的方向余弦矩陣為：

直角坐標系中的應力張量與曲線坐標系中應力張量可按下式轉換：

2 斜頂巷道應力分析

以淮南礦業集團潘三煤礦17102(3)工作面運輸巷為例，分析斜頂巷道圍巖應力和應力集中系數分布特征。此巷道斷面如圖3所示。依據地應力測試結果，取垂直應力σV=16.8MPa，水平應力σH=13.3MPa，剪應力τ=0.5MPa。

圖3 斜頂巷道斷面(mm)

2.1 共形映射函數求解結果

依據文獻[15，16]中提出的共形映射函數求解方法，運用科學計算軟件編程求解斜頂巷道外域到單位圓內的共形映射函數的系數An和Bn。Laurent級數的階數N不同時，共形映射函數的映射圖形如圖4所示。由式(4)可計算得到共形映射函數的最大絕對誤差隨階數N增加的變化曲線，如圖5所示。

圖4 階數N不同時共形映射函數的映射圖形

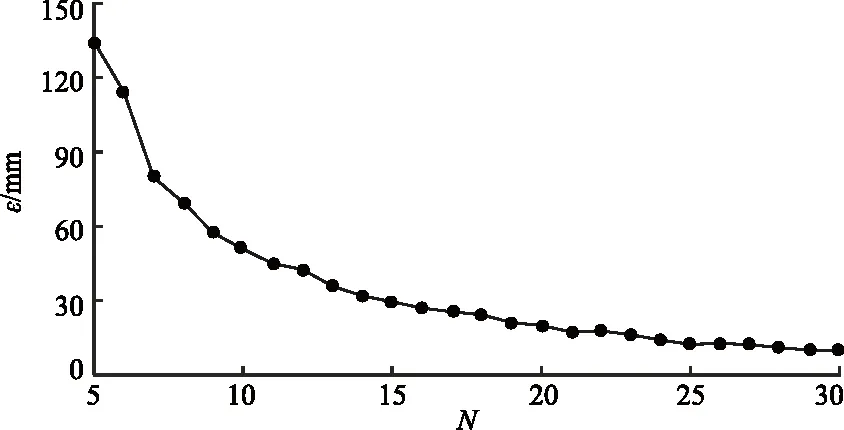
圖5 最大絕對誤差隨階數N增加的變化曲線

由圖4和圖5可知，隨著階數N的增加，共形映射函數很快收斂到巷道斷面邊界。同時，共形映射函數的最大絕對誤差迅速減小。當階數N大于22時，共形映射函數的最大絕對誤差減小緩慢，且此時的最大絕對誤差很小。因此，取階數N為22。系數An和Bn的求解結果見表1。

表1 斜頂巷道共形映射函數系數

由圖5可知，真實巷道邊界與求解得到的斜頂巷道共形映射函數近似的巷道斷面邊界之間的最大絕對誤差為14.3mm。由式(2)可得四個巷角的曲率半徑分別為31.4mm、31.1mm、26.7mm和56.8mm。對比文獻[15，16]中共形映射函數的誤差可得，斜頂巷道共形映射函數精度很高，同時考慮到實際工程中超挖和欠挖現象，本文求解得到的共形映射函數可滿足計算要求。

2.2 斜頂巷道主應力和主應力集中系數分布規律

圖6 斜頂巷道主應力分布

由圖6(a)和圖7(a)可知，斜頂巷道最大主應力和最大主應力集中系數呈現腎臟形分布。兩幫最大主應力和最大主應力集中系數大于頂底板。在巷道角點處，最大主應力和最大主應力集中系數達到最大值，最大主應力最大值超過了35MPa，最大主應力集中系數最大值超過了4.5。

由圖6(b)和圖7(b)可知，斜頂巷道最小主應力和最小主應力集中系數呈現花形分布。巷道表面的最小主應力和最小主應力集中系數為0。在兩幫和頂底板圍巖中部，最小主應力和最小主應力集中系數較小。在巷道角點處，最小主應力和最小主應力集中系數達到最大值，最小主應力最大值超過了35MPa，最小主應力集中系數最大值超過了2.5。

由圖6(c)和圖7(c)可知，兩幫最大剪應力和最大剪應力集中系數大于頂底板。由Mohr-Coulomb巖石強度準則可知，圍巖內一點最大剪應力越大，圍巖發生破壞失穩的可能性越大。由此可知頂底板較兩幫穩定。在巷角處，最大剪應力和最大剪應力集中系數達到最大值，最大剪應力最大值超過了35MPa，最大剪應力集中系數最大值超過了8。表明巷角是斜頂巷道中穩定性最差的部位，加強巷角的支護強度有利于維護巷道穩定。

圖7 斜頂巷道應力集中系數力分布

3 結 論

1)斜頂巷道的共形映射函數的最大絕對誤差為14.3mm，四個巷角的曲率半徑分別為31.4mm、31.1mm、26.7mm和56.8mm。斜頂巷道的共形映射函數精度很高，可用于斜頂巷道應力分布求解。

2)斜頂巷道圍巖最大主應力、最小主應力、最大剪應力及其應力集中系數的最大值均出現在巷角處，主應力分量最大值均超過35MPa，主應力集中系數最大值分別超過4.5、2.5和8，巷角是斜頂巷道的薄弱部位，加強對巷角的支護強度有利于提高斜頂巷道圍巖的穩定性。

3)兩幫最大剪應力整體上大于頂底板，同時，最大剪應力集中系數也大于頂底板，兩幫穩定性較頂底板穩定性低，加強對巷道兩幫的支護強度有利于提高巷道整體穩定性。