半波長管傳聲損失分析*

王 恒 毛崎波 胡龍軒 王淵德 謝 冉

(南昌航空大學飛行器工程學院 南昌 330063)

0 引言

利用聲波疊加干涉原理的干涉管，因其簡單的結構和優秀的消聲性能在噪聲控制領域中備受關注，例如著名的1/4 波長管和Herschel-Quincke(HQ)管。1/4 波長管利用管口入射聲波在管端反射后，形成頻率相同的聲波發生疊加干涉作用[1]。1/4 波長管因其簡單的結構和良好的消聲性能，為許多工程領域提供了理想的解決方案，例如：在航空降噪領域，Oschwald等[2]利用1/4波長管干涉特性解決航空發動機的燃燒不穩定問題，通過實驗證明加入1/4 波管后，燃燒室固有頻率發生改變，提高燃燒的穩定性；在汽車降噪領域，劉濤等[3]將1/4 波長管運用在增壓發動機進氣系統，有效解決渦輪增壓器的氣流嘯叫噪聲。HQ 管利用兩個分支管路徑的不同改變了聲波的相位[4]，聲波疊加干涉從而達到降噪的效果。HQ 這種結構具有很大的可改造性，使得其在降噪領域具有很大發展潛力，為此出現了大量基于HQ 管的研究。早期，Selamet等[5]提出一種改進的多分支管并聯模型，并且推導出傳聲損失理論模型；Desantes 等[6]在傳統HQ 管兩分支管中引入一根連接管，給出一種推導這種帶有連接管理論模型的方法。隨后，Torregrosa 等[7]改變了分支管橫截面積，設計了一種橫截面積漸變的HQ 管，以此來提高傳統HQ 管的消聲性能；Poirier 等[8]提出了一種HQ 管與聲襯的組合模型，這種組合模型可以充分發揮二者的特性，達到更進一步的消聲效果。在近期，Kim 等[9]設計了一種利用周期陣列的諧振管阻滯振速傳播進而形成相位差的虛擬HQ 管，并且通過改變諧振管的排布方式實現降噪頻率的可調節；Arjunan[10]利用3D 打印技術數字化打印特點，實現了HQ管數字化制造，使得HQ 管可以在指定頻率降噪。除了上述理論實驗研究，在工程應用中也可以看到HQ 管的身影，例如：Hallez[11]就將傳統HQ 管應用在航空發動機進口降噪，在實際的測試中表明在特定頻率下具有明顯的降噪效果；Zhu 等[12]采用半主動控制HQ管對發動機的排氣噪聲進行控制，測試結果表明在50～150 Hz頻率的范圍內可以平均降噪35 dB。

以上論述中表明，無論在理論還是在實際工程應用中，1/4波長管與HQ管都表現出良好的消聲效果，又因為二者具有相似的聲學性能，為此本文提出了一種基于這兩種干涉管的新的半波長管，如圖1所示，其兩端開口和傳統半波長管相同[13]，但其另一端并不敞口而是連接主管類似于HQ 管，且其兩端口位于同一主管橫截面積上，使得相干波在同一主管橫截面相遇，從而達到干涉降噪的效果，這又與1/4 波長管相似，這種結構布局方式使得這種新的干涉管占用空間更小，而且具有與1/4波長管和HQ管類似的消聲性能。本文首先推導出半波長管傳聲損失理論模型，然后基于理論模型探究了傳聲損失的影響因素，根據各影響因素對寬頻帶傳聲損失模型進行了計算分析并且得出了較好的寬頻帶降噪效果，最后對理論模型進行實驗驗證和管端部修正，驗證理論模型的可靠性。

圖1 一種新型半波長管Fig.1 A new resonance tube

1 傳聲損失計算模型

圖2是本文提出的半波長管的多分支干涉管理論模型示意圖。圖中各分支管管徑均勻且串聯排布，同時假設管中無流且聲波以平面波傳播。

對于圖2所示的整個復雜的管道系統，由n個虛框中的基本子系統組成，就其中任意一個基本子系統而言，其進出口間的聲壓p和體積速度v可以表示為

圖2 串聯排布的半波長管示意圖Fig.2 Schematic diagram of half wavelength tube in series arrangement

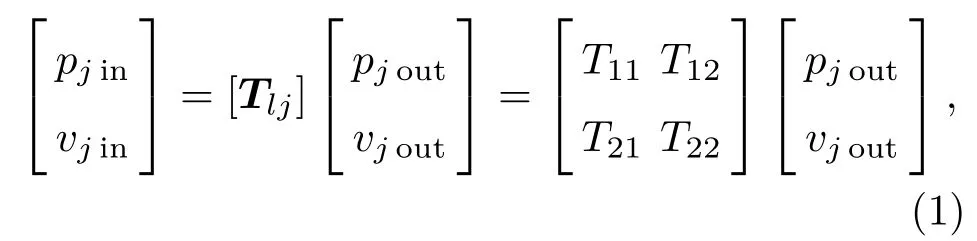
式(1)中，下標“j”代表第j個子系統，[Tlj]為該子系統中的傳遞矩陣，其中的4 個元素T11、T12、T21和T22稱為四極參數[14]。同時，對于該子系統中的分支管的兩端的聲壓p和體積速度v可以表示為

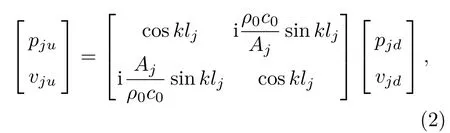
式(2)中，k=ω/c0為波數，ω為角頻率，ρ0和c0分別為空氣密度與聲速，Aj和lj為第j個子系統中分支管的面積與管長，下標“ju”和“jd”分別為第j個子系統中分支管的上游與下游端口。

在上述的子系統中，在主管與分支管的連接處，即分支管的上下游端口，由壓力和體積速度連續條件可得

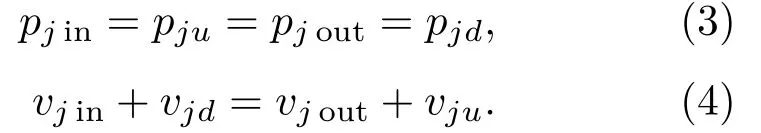
從式(2)和式(3)可得

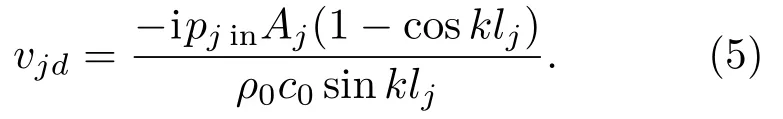
將式(5)和式(1)代入式(2)可得

由式(1)～式(6)可得傳遞矩陣[Tlj]的所有四極參數的表達式，即

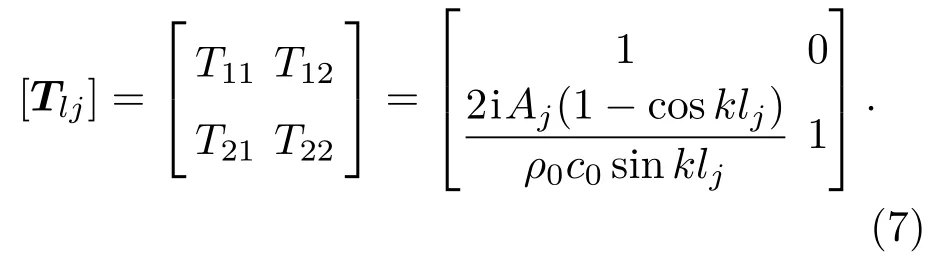
對于圖2任意第j個子系統的進出口狀態變量的傳遞關系可以通過式(7)表示，為了進一步得到整體管道系統的傳聲損失，只需要將各個子系統串聯，則任意第j個子系統與第(j+1)個子系統間狀態變量的傳遞關系可以表示為

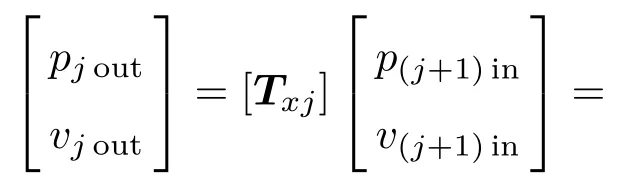
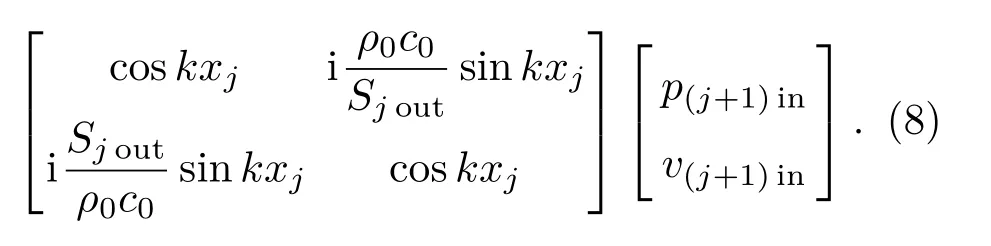
圖2所示的整體管道系統由n個子系統通過相應的主管連接組合而成，為此可以通過如下傳遞關系式將整個系統進出口的聲壓p和體積速度v可以表示為

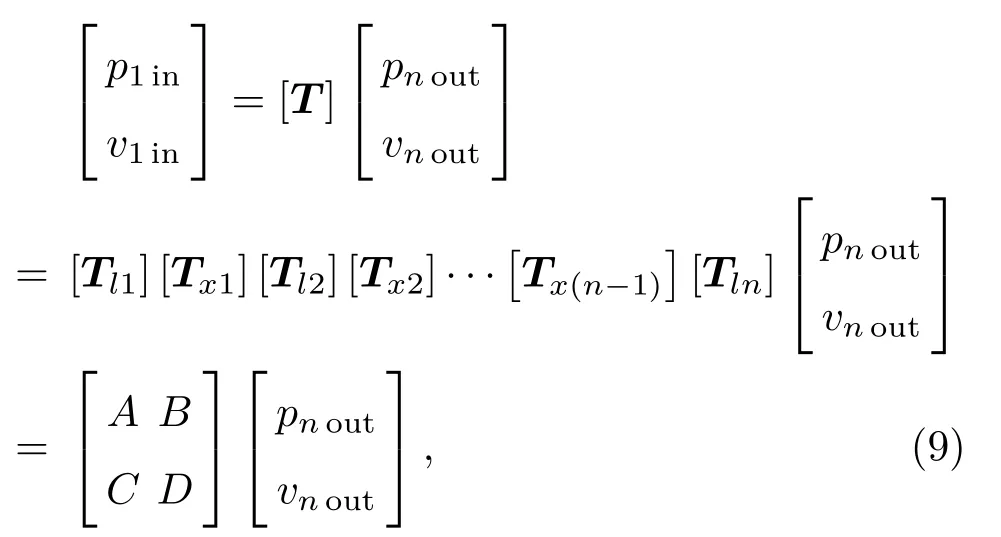
式(9)中，[T]為整個系統總傳遞矩陣，A、B、C和D為總傳遞矩陣的四極參數，[Tl1]、[Tl2] 和[Tln]為子系統傳遞矩陣([Tlj]，其中j= 1，2，···，n)，[Tx1]、[Tx2]和[Tx(n-1)]為對應的相鄰子系統間的傳遞矩陣([Txj]，其中j= 1，2，···，n-1)。從而整個系統的傳聲損失表達式可以由四級參數定義為[14]

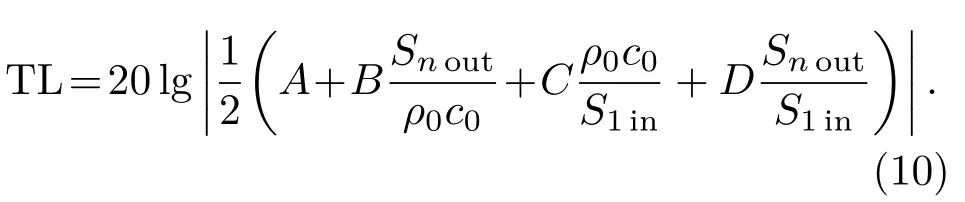
當已知分支管管數量和參數時，通過上述推導過程，可以得到四極參數A、B、C和D，將所得四極參數代入式(10)可以得出任意數量分支管串聯模型的傳聲損失。

假設只有一個半波長管時，傳聲損失表達式為[14]

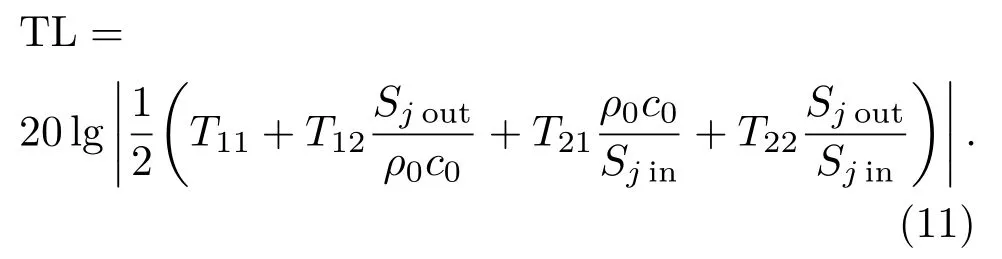
當Sjin=Sjout時，將傳遞矩陣[Tlj] 中四極參數代入式(11)可得

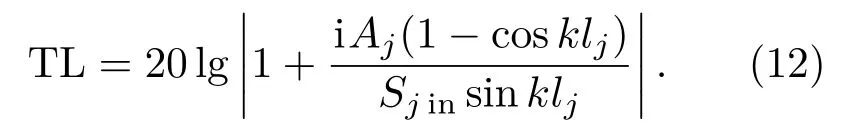
當進口端主管與出口端主管橫截面積相等時，即Sjin=Sjout時，可知該子系統產生共振的條件為

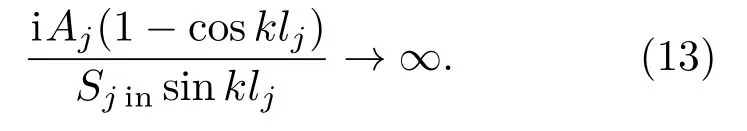
由此得到

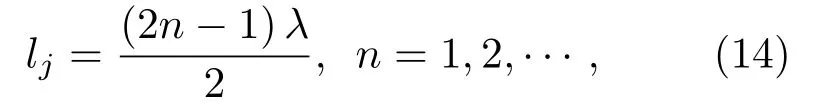
其中，λ為波長。由式(14)可知，當分支管長為半波長的奇數倍時產生共振，所以稱之為半波長管，其共振頻率為

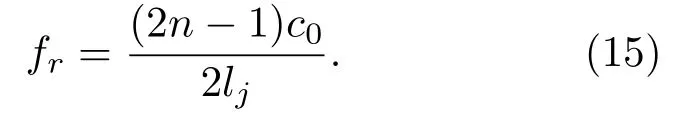
當xj=0時，簡化為同一位置的多分支1/2管模型。

因為xj= 0，所以式(9)中，子系統之間的傳遞矩陣，將其和式(7)代入式(9)可得

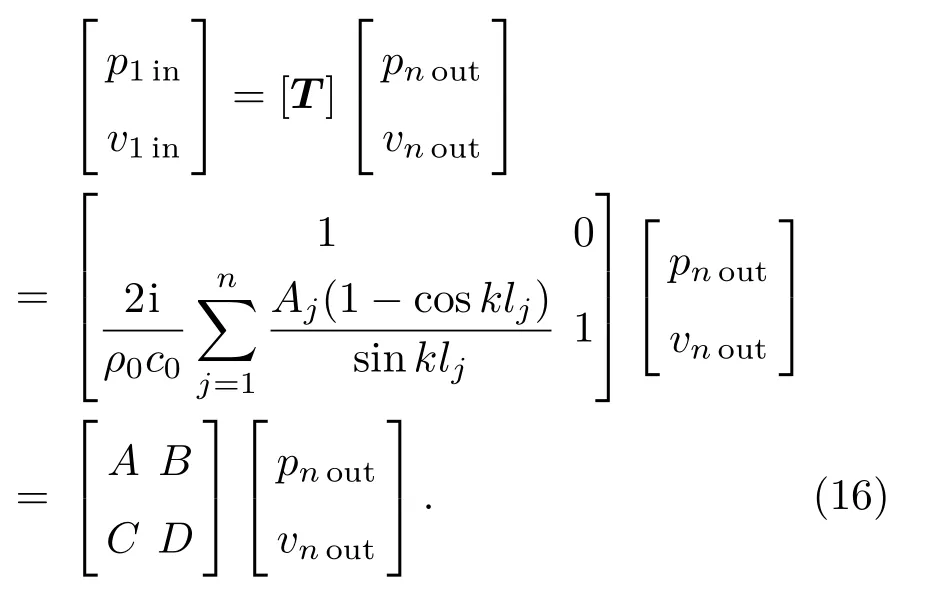
當進出口主管橫截面積相等時(Sin=Sout)，將式(16)中四極參數值代入式(11)可以得到任意數量分支管同一位置時的傳聲損失為

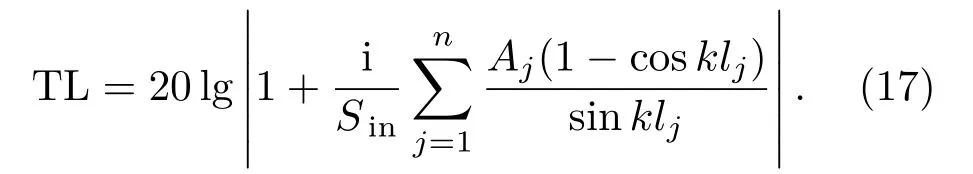
2 數值計算

在上述的理論模型中，推導出了半波長管的傳聲損失理論模型，但在多分支管模型時，式(9)和式(17)將會變得極其復雜，難以推導出對傳聲損失的影響因素。為了更直觀探究出串聯與并聯模型中對傳聲損失的影響因素，下面基于前文推導的理論模型，進行了半波長管模型在不同管徑和管長下以及在不同分支管距離下的傳聲損失數值計算，并將數值計算的結果統一表示為0～1500 Hz 上的傳聲損失曲線。

2.1 管徑和管數對傳聲損失的影響

分析不同管徑和管數在半波長管模型x=0 m(并聯)時和x=0.1 m (串聯)時對傳聲損失的影響，假設主管管徑D=0.1 m，分支管管長l=0.5 m，并且各分支管長度相同。

首先，三分支管模型，圖3表示管徑變化時的傳聲損失。通過對圖3(a)觀察分析可知，x= 0 m 時，即同一位置多分支管時，增加分支管管徑，即增加分支管總橫截面積可以增加傳聲損失，拓寬固有頻率處的消聲峰，增加其消聲性能。通過對圖3(b)觀察分析可知，x=0.1 m時，多分支管串聯時，增加分支管管徑，同樣可以增加傳聲損失。

其次，分支管的橫截面積之和保持不變，而改變分支管數目，結果如圖4所示。對圖4(a)結果分析可知，x=0 m時，不管每個模型中分支管數量是否相同，只要總的分支管橫截面積相同，傳聲損失也相同。對圖4(b)結果分析可知，x= 0.1 m 時，與x=0 m時類似，傳聲損失基本保持不變。

最后，對比圖3、圖4中x= 0 m 和x= 0.1 m可以發現：在分支管長不變的情況下，無論是串聯還是并聯模型，改變管徑和管數都不會改變模型的固有頻率，這與理論模型相一致，由式(16)可知，并聯模型的共振頻率的條件為sinklj= 0∪(1-cosklj)≠ 0，由共振條件推得共振時的條件與式(14)相同，共振頻率也與式(15)相同；在管徑和管數相同的情況下，串聯模型與并聯模型的傳聲損失基本相同。

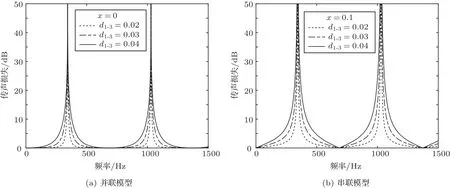
圖3 兩種模型不同管徑傳聲損失Fig.3 Sound transmission loss of the two models with different pipe diameters

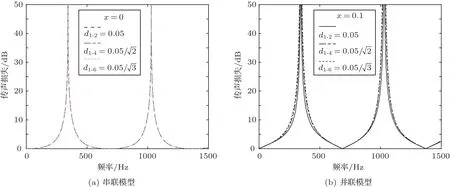
圖4 兩種模型不同管數傳聲損失Fig.4 Sound transmission loss of the two models with different number of the tube

2.2 管長對傳聲損失的影響

探究管長對半波長管傳聲損失的影響，同樣主管橫截面積不變(主管管徑D= 0.1 m)，分支管管徑保持不變。從2.1 節管徑對傳聲損失影響的結果可知，當主管管徑已知，分支管管徑的增加可以拓寬消聲頻率，因此為了獲得更好的消聲效果，所以選擇分支管管徑為d= 0.05 m，支管間的距離為x=0 m或者x=0.1 m。

為了更清楚展示出管徑改變的計算結果，選擇10 分支管模型進行計算，并通過式(15)計算相應的固有頻率，各分支管的長度和固有頻率如表1所示。

表1 10 分支管模型物理尺寸Table 1 Physical dimensions of 10 branch tube model

由理論模型可知，無論是串聯模型還是并聯模型，固有頻率都是由分支管的長度決定的，所以將串聯和并聯模型在不同管長下的傳聲損失計算結果進行對比，計算結果如圖5所示。

圖5 串并聯模型不同管長傳聲損失計算結果Fig.5 Calculation results of sound transmission loss of different tubes in series and parallel models

在圖5所示的計算結果中可以看出，分支管管距為零與不為零的相同之處在于都產生了共同消聲尖峰，這與之前的理論模型相符合，由于兩種模型的物理尺寸相同，所以二者具有相同的共振峰；從兩者的傳聲曲線可以看出，當各分支管之間的長度差適當，即各分支管之間固有頻率差一定，都可以形成寬頻帶傳聲損失。差異在于從形成的頻帶可以看出，一階消聲頻帶二者差距不大，但是在二階消聲頻帶，串聯的傳聲損失要明顯高于并聯。

2.3 分支管之間的距離對傳聲損失的影響

本節計算所用的10 分支管模型與表1相同，探究分支管之間距離對傳聲損失的影響，分別取x等于0.001 m、0.01 m、0.1 m、0.2 m 和0.3 m，計算結果如圖6所示。

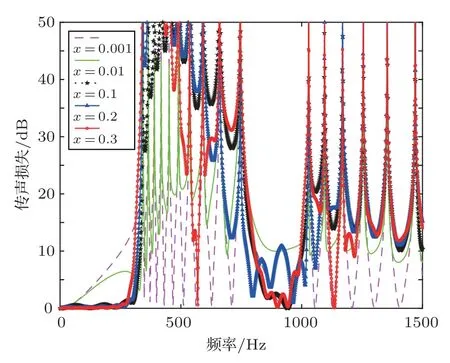
圖6 不同分支管管距對傳聲損失的影響Fig.6 Influence of different branch tube spacing on sound transmission loss

從圖6中可以看出當分支管之間的距離較小(x= 0.001 m)時，基本不會形成頻帶消聲效果；隨著距離的增加，寬頻帶的消聲效果開始出現，并且頻帶的消聲量級也在增加，同時也可以看出隨著距離的增加，寬頻帶的穩定性在降低；當x=0.3 m時，頻帶會出現劇烈的波動，頻帶也隨之變窄。綜合對比可以看出在x=0.1 m時寬頻帶的消聲效果較好。

2.4 寬頻帶傳聲損失尺寸設計

在以上管徑、管長以及支管管距對傳聲損失影響的系統的探究中，應用數值計算的方法，得出了本文所提出的半波長管的各種影響因素對其傳聲損失作用規律，將在此基礎上，進一步對寬頻帶傳聲損失進行尺寸設計。

降噪頻帶設定為350～1350 Hz，要求頻帶內不低于20 dB的消聲量級。基于理論模型通過數值計算軟件中的fmincon 函數進行優化計算，得到寬頻帶傳聲損失的管長尺寸如表2所示，結果如圖7所示。

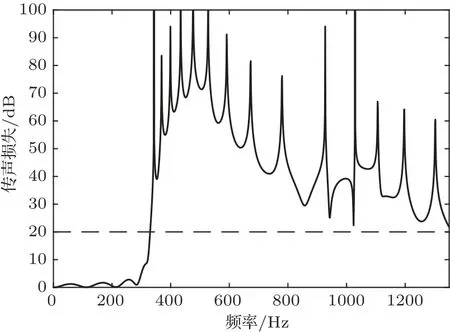
圖7 寬屏帶傳聲損失Fig.7 Broadband sound transmission loss

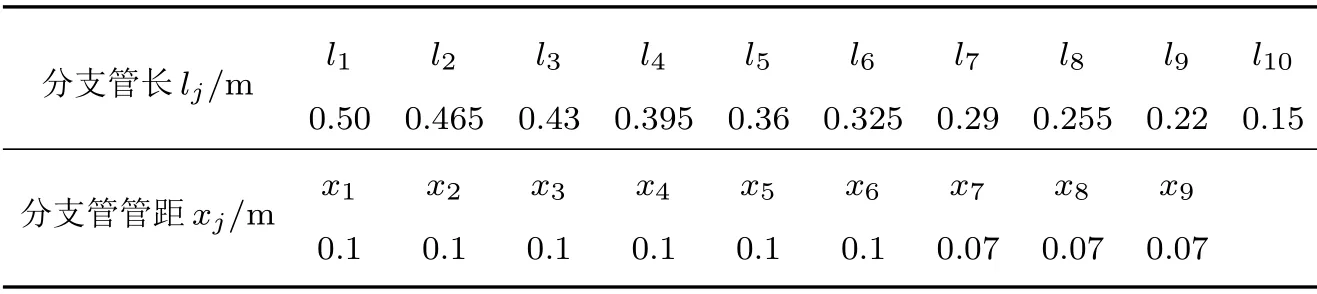
表2 寬頻帶傳聲損失模型尺寸Table 2 Dimensions of broadband transmission loss model

由圖7可知，利用本文所推導理論模型和數值計算結果，對半波長管尺寸設計，可以實現精確的寬頻帶傳聲損失控制，從而達到目標要求。

3 實驗驗證和端部修正

為了對理論結果進行驗證以及對管端部在非平面波引起的誤差進行修正，對理論模型進行了實驗驗證并且采用實驗的方法進行端部修正。

首先，搭建實驗裝置，然后采用四傳感器的傳遞函數法對不同管長單分支管模型的固有頻率進行了測量，主管和分支管尺寸如表3所示，其實驗裝置如圖8所示。

圖8 實驗測量裝置Fig.8 Experimental measuring device

其次，采用實驗的方法對理論模型中管端部進行修正[15]。單分支管時，分別測量了5 根不同長度分支管的傳聲損失，其中各管尺寸如表3所示，結果如圖9所示，基于傳聲損失的實驗數據得到各管的固有頻率。將理論值對照實驗所得固有頻率進行修正得出端部修正系數Δl= 3.75r(r為分支管半徑)，修正后固有頻率計算公式(式(15))變為，修正后的理論與實驗結果對比如圖10所示。

表3 主管與分支管尺寸Table 3 Dimensions of main and branch tube

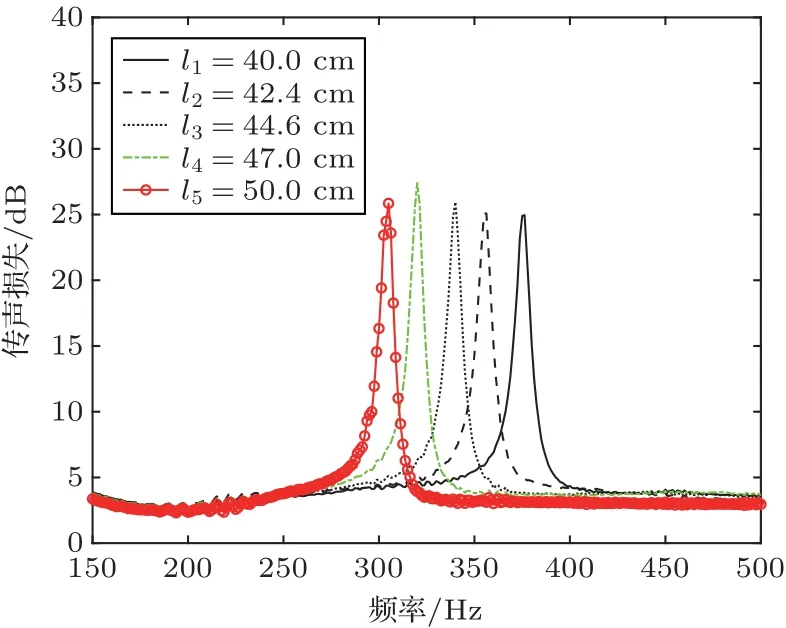
圖9 不同管長傳聲損失Fig.9 Transmission loss of tubes of different lengths

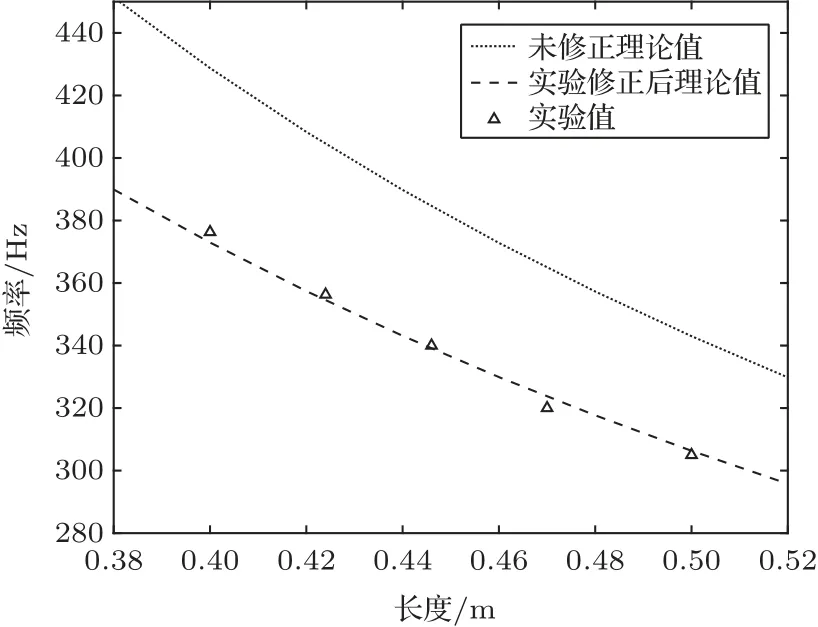
圖10 分支管端部修正結果Fig.10 The end correction result of branch pipe

最后，引入端部修正后對傳聲損失理論模型進行驗證。當管長同為0.5 m 時，分別對單分支管、雙分支管和三分支管的傳聲損失進行測量，其中雙分支管與三分支管管距為0.06 m，分支管與主管其余具體尺寸如表3所示，對比實驗測得的結果對修正后的理論結果進行驗證，如圖11所示。

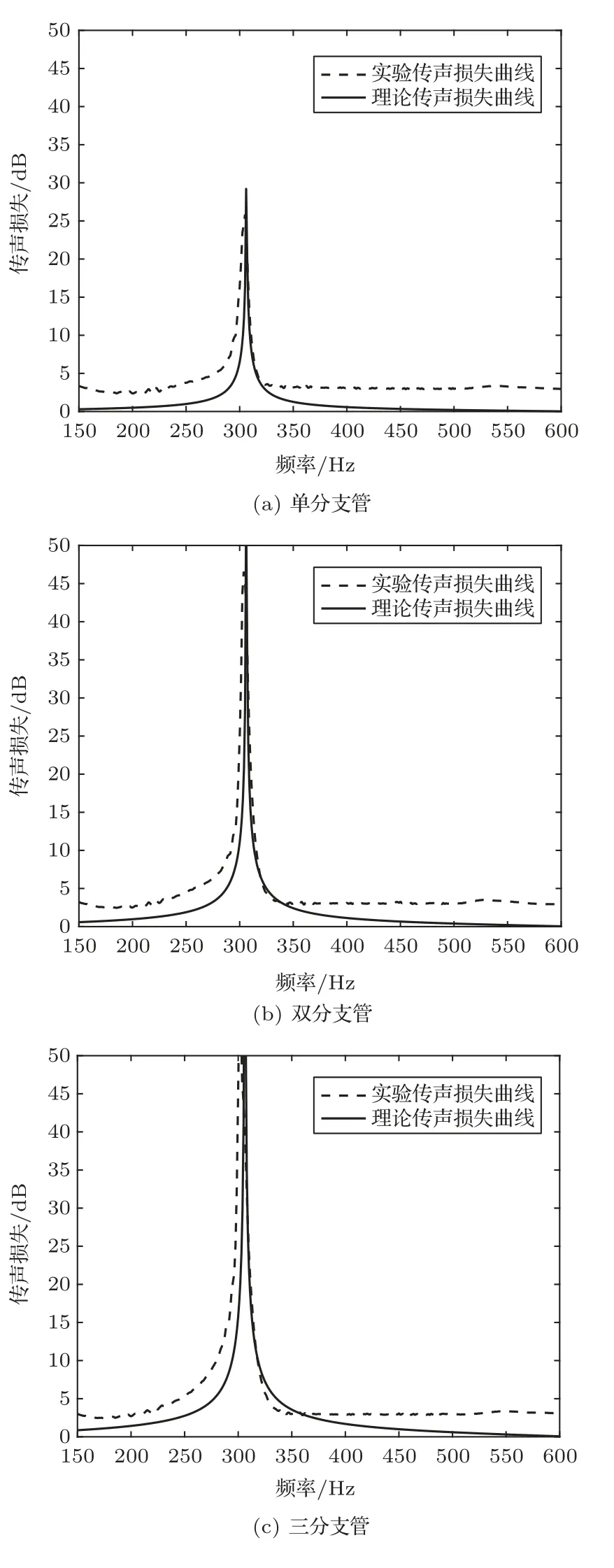
圖11 不同分支管數理論與試驗對比Fig.11 Comparison of theory and experiment with different branch number

4 結論

本文首先提出一種新的半波長管模型，并推導出任意分支管理論模型；然后通過數值計算分析了傳聲損失影響因數，根據影響因數分析的結果以及數值計算軟件計算結果設計了寬頻帶傳聲損失的模型尺寸，得出350～1350 Hz 且不低于20 dB 的寬頻帶消聲效果，證明本文所提出的半波長管具有良好的消聲潛力；最后通過實驗方法對理論模型進行修正和驗證，修正理論模型的同時也證實理論本文所推導理論模型的可靠性。未來的研究中可以將其設計為一種空間折疊結構聲學超材料，使得其具有完美吸聲效果以及亞波長厚度[16-17]，使得在各領域應用中具有更大的潛力。