基于FVM 方法的彎道斜交橋洪水影響研究及河勢分析

牛 嬌，成靜清，鄢笑宇，賈 磊，王志超

(1.江西省水利科學院，江西 南昌 330029；2.水利部鄱陽湖水資源水生態環境研究中心，江西 南昌 330029；3.江西省鄱陽湖水資源與環境重點實驗室，江西南昌330029)

水動力學模型目前是研究水流運動規律的重要方法之一。 隨著數值模擬技術的不斷進步，該方法正被應用于越來越多的工程項目和研究當中，如評估工程建設對洪水過程的影響，研究人為因素干預下的河道水文特征和河勢地形演變趨勢等。

早在1967 年Liggett等[1]便利用顯示差分格式和矩形網格建立了二維水動力學模型來模擬洪水演進過程。 李暢游等[2]在湖泊二維水動力學模型基礎上考慮了蒸發、風力因素，模擬研究中國干旱半干旱地區湖泊烏梁素海的水動力學過程。 王宗志等[3]采用Preissmann 四點隱式差分和模塊化建模技術，構建考慮河道下滲的海河流域漳衛河水系河網洪水模型，模擬研究不同調度方案下的洪水特點。Akanbi等[4]使用有限元法，通過單元積分來構造函數和導數之間的關系，并用插值函數來近似連續函數解，成功模擬了洪水波在干河床上的運動過程。 李大鳴、范玉等[5-7]分別基于有限元方法和有限體積方法求解淺水方程，建模分析河道和蓄滯洪區洪水演進特點及人為因素對洪水的影響。 姜曉明等[8]、吳鋼鋒等[9]采用基于黎曼近似解Godunov格式的有限體積方法模擬了潰堤洪水的演進過程與淹沒范圍。 張震[10]和蘇暢[11]利用Mike 21 軟件研究評估涉水工程建設對洪水的影響。 Wang[12]采用有限體積方法模擬分析鄱陽湖入江水道某引水工程建設下的水下地形演變特征。 陳建等[13]采用Mike21 軟件計算某水庫建設和運行對下游河流地貌過渡區水文情勢的影響。劉鑫等[14]采用Mike 3 軟件模擬研究在裁彎取直工程和丁壩群的影響下的河道流態特征。 王志超等[15]采用有限體積方法模擬預測撫河尾閭改道工程建設下的尾閭洪水特性變化。

本文基于有限體積法，采用二維非結構網格，用Fortran 語言編譯建立跨河灣斜交橋所在河段水動力學模型。 采用該模型針對P=10%、P=20%洪水條件下橋梁建成后對上下游水位、流速和河勢的影響進行分析。 研究區域橋位所在河段彎曲，且橋梁與河道斜交，本研究旨在探討橋墩導流作用對洪水及河勢的影響，為相關工程設計提供參考。

1 數學模型理論

采用靜水壓假定和Boussinesq 近似，模型控制方程的動量方程、連續方程原始形式如下。

連續方程:

動量方程:

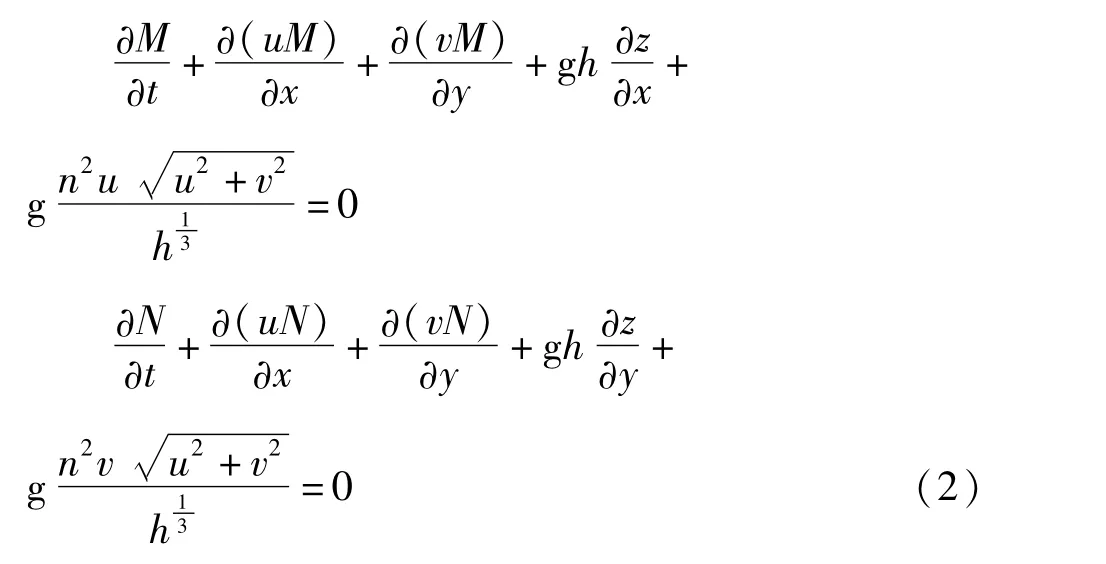
式中 h——水深；z——水位；M、N——沿x、y方向上的單寬流量；u、v——沿x、y方向的平均流速；n——糙率；g——重力加速度。

將控制方程轉換成Godunov格式然后用有限體積方法離散，采用Roe格式的近似Riemann 解計算界面通量[8-9]。

2 模型的建立

2.1 模型概況

本文以某擬建跨河彎道斜交橋為例，橋位所在處兩岸為山體，岸坡較陡峻，植被較好，橋址區域內表層地層巖性自上而下分別為第四系全新人工堆積層(Q4ml)雜填土、第四系全新統沖洪積層(Q4al+pl)粉質黏土、第四系全新統殘坡積層(Q4el+dl)粉質黏土、下伏基巖為寒武系(∈1)千枚巖，其中基巖最大埋深為1.8 m。 橋位所在水域概況見圖1，橋位所在處河寬約300 m，大橋與河流斜交，夾角65°，大橋兩側橋臺位于山丘坡上，9 座橋墩布置在河道內，主橋跨度80 m，其他孔跨在24.70 ～40.85 m，橋墩寬度3.30 m，采用圓弧墩設計，樁基礎。 全橋孔跨布置及平面尺寸見圖2。

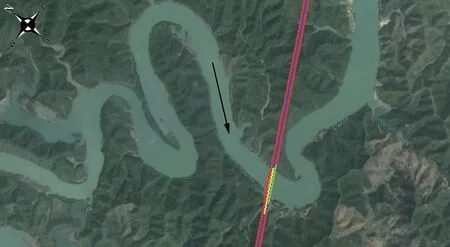
圖1 橋位所在河段概況

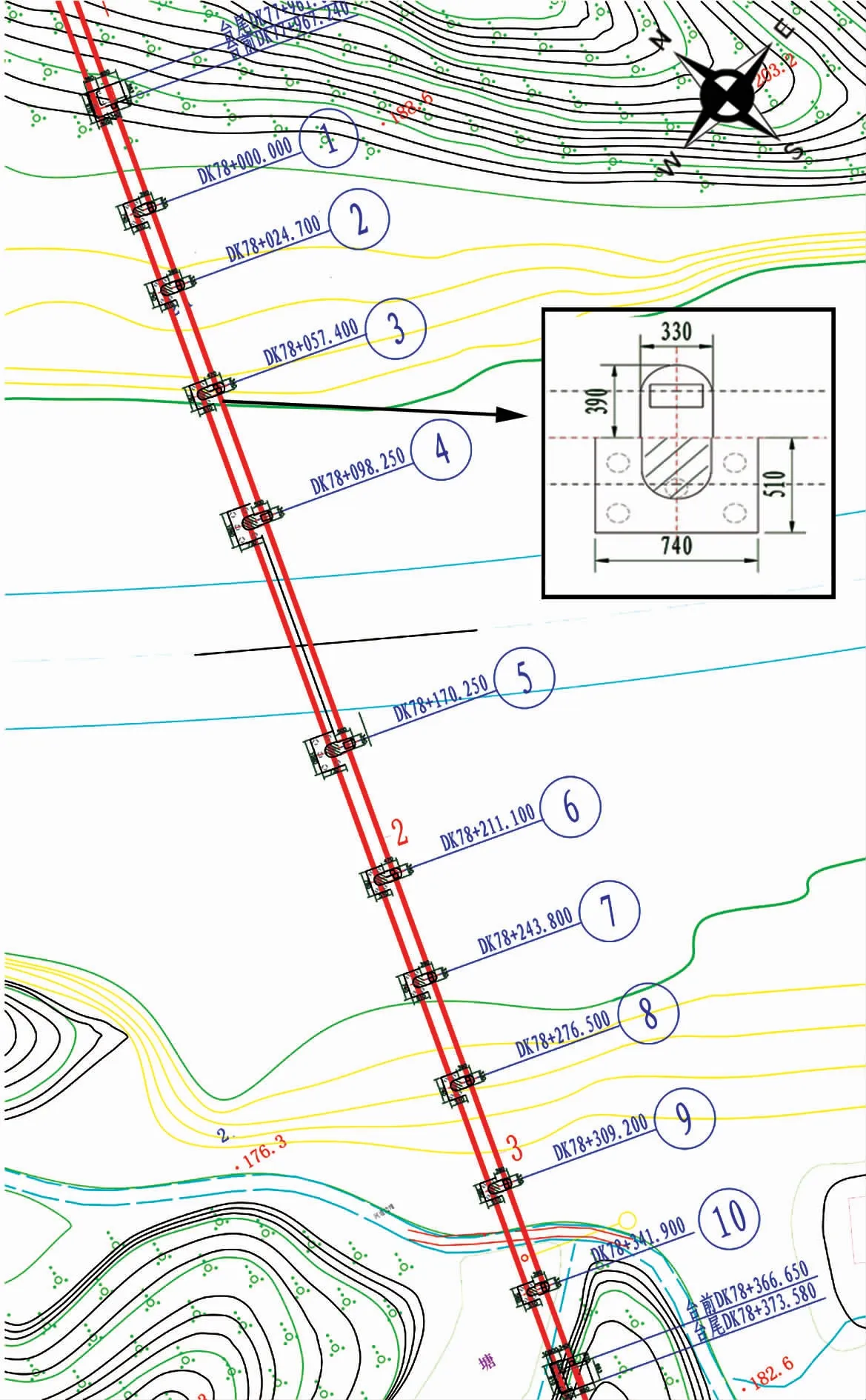
圖2 橋跨布置及平面尺寸

2.2 計算范圍

本次模擬分析大橋建設對工程河段水位及河勢的影響，需建立包括彎道在內的河段二維模型，模型計算采用河道上下游實測地形資料(1:5 000)，考慮大橋建設對河道上下游的影響范圍，模型研究范圍為橋址下游600 m，上游600 m，模型范圍長1.20 km。

2.3 模型網格

在進行天然河道的數值模擬計算時，由于天然河道一般邊界曲折、地形復雜，水流運動處于一個狹長而不規則的復雜區域內，邊界形狀對流場變化的影響很大，因此在進行天然河道數值模擬計算時，多采用非結構網格。

橋址處河道寬約300 m，上下游最窄處約為200 m，河槽水深0.1 ～15.0 m。 網格采用非結構網格，對橋墩附近區域進行局部網格加密，共布設22 700 個單元，網格平均面積約為25 m2。 模型網格布置見圖3，橋墩處局部網格見圖4。 工程前后模型網格結構和布置相同，通過設置橋墩網格為不過水邊界來反映工程的影響。

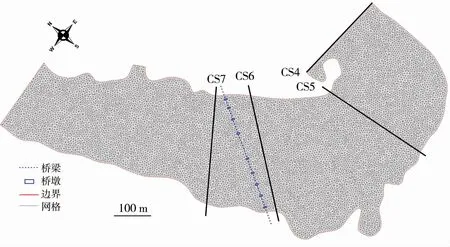
圖3 橋梁布置及模型網格

圖4 橋墩處網格

2.4 模型驗證

由于工程區域水文資料缺乏，故二維模型的驗證以該研究區域一維水面線成果為依據，見圖5，在模型上布置3 個驗證斷面，二維模型驗證成果見表1(邊界流量為2 230 m3/s)。 各斷面二維計算值的誤差均小于0.05 m，所建模型可用于方案計算。

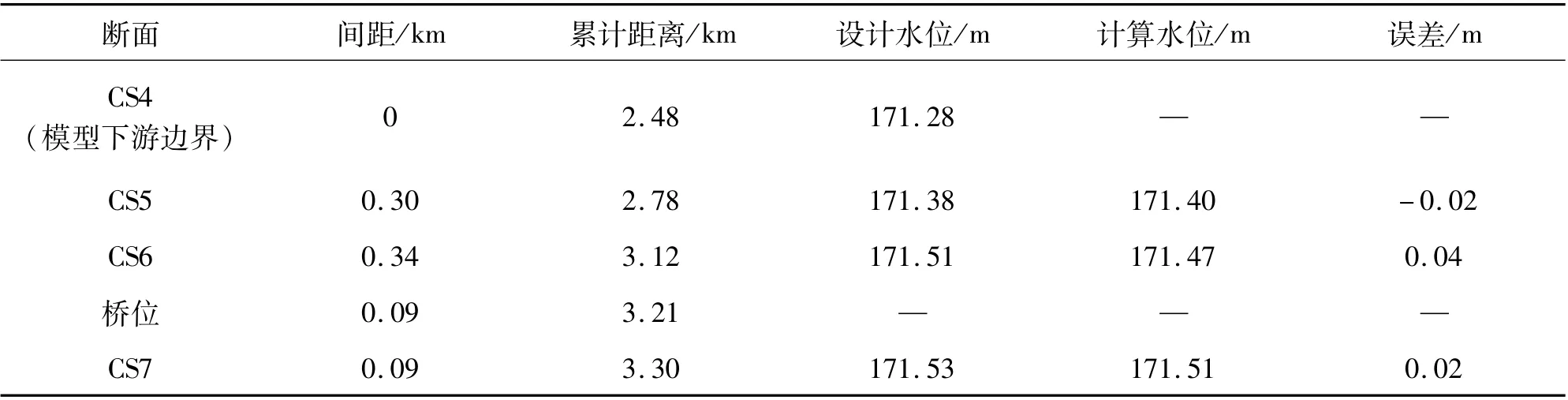
表1 水位驗證成果

圖5 工程所在河道水面線

3 模擬與分析

本次研究建立高分辨率的二維數學模型，分析P=10%、P=20%洪水條件下的工程影響。 基于大橋下游水文站點實測流量資料，采用水文比擬法得到模型上游邊界流量，下游邊界水位根據水面線法推求得到，圖5 為工程所在河段水面線成果。

3.1 水位影響

受橋墩阻水作用的影響，各頻率洪水條件下，建橋后上游水位有所壅高，模型入口處平均壅高約0.02 m；橋梁下游受影響較區域較上游要小，水位變化在±0.01 m的范圍主要分布在橋墩附近60 m以內的區域(表2)。 橋墩迎水面水位壅高，背水面水位下降，由于橋墩布置與河道流速呈一定的夾角，橋梁下游水位呈現左岸壅高、右岸下降的特點(圖6)。

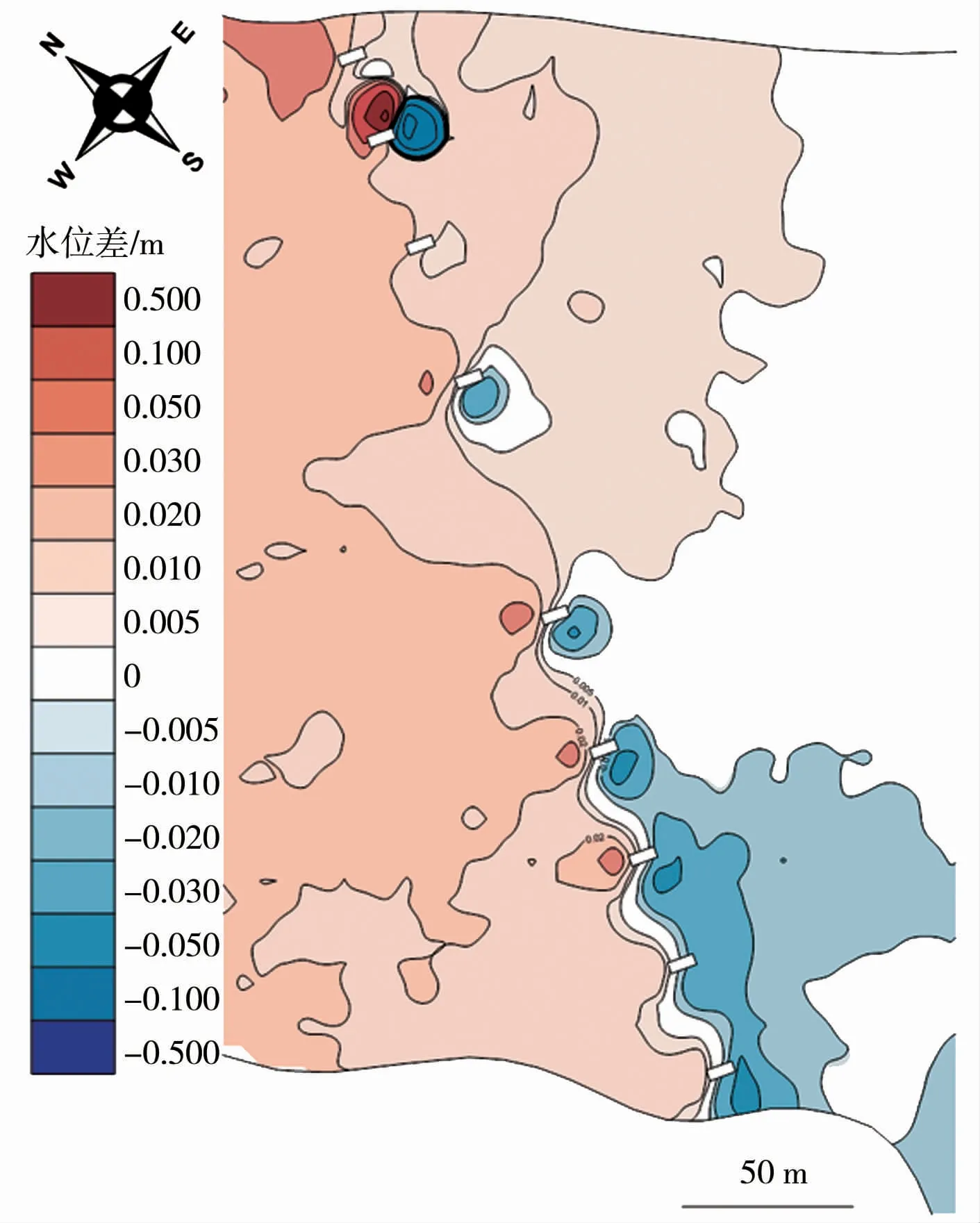
圖6 水位變化等值線

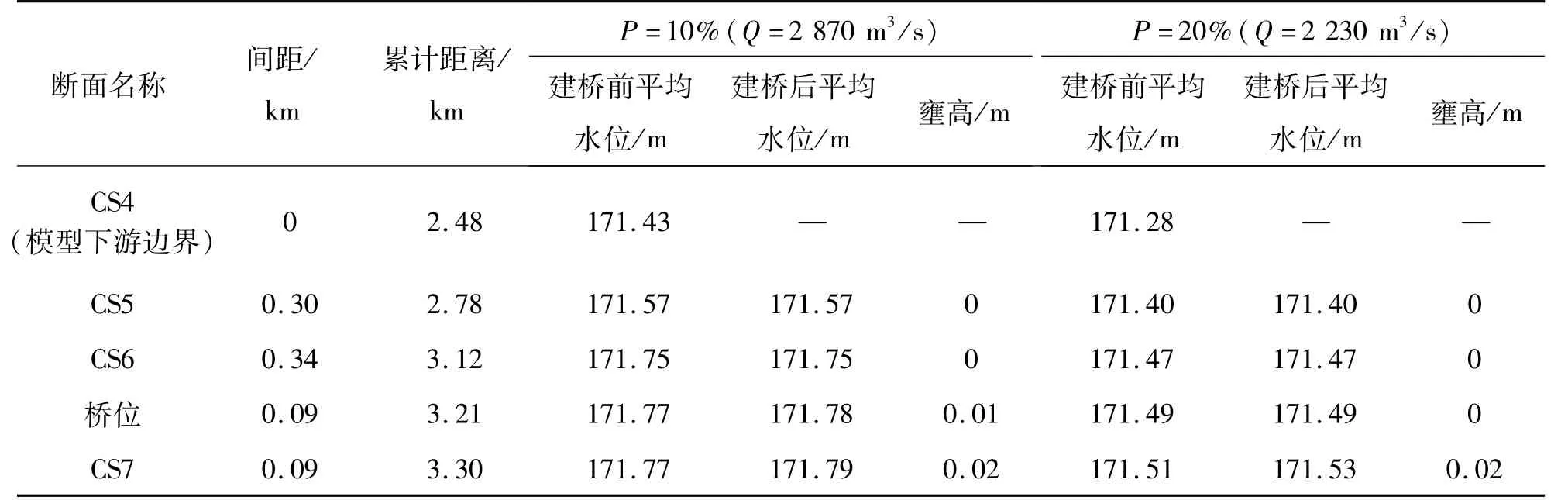
表2 不同頻率各斷面平均水位壅高值

3.2 流場影響

工程附近局部流場的對比見圖7，工程前后流速變化等值線見圖8。

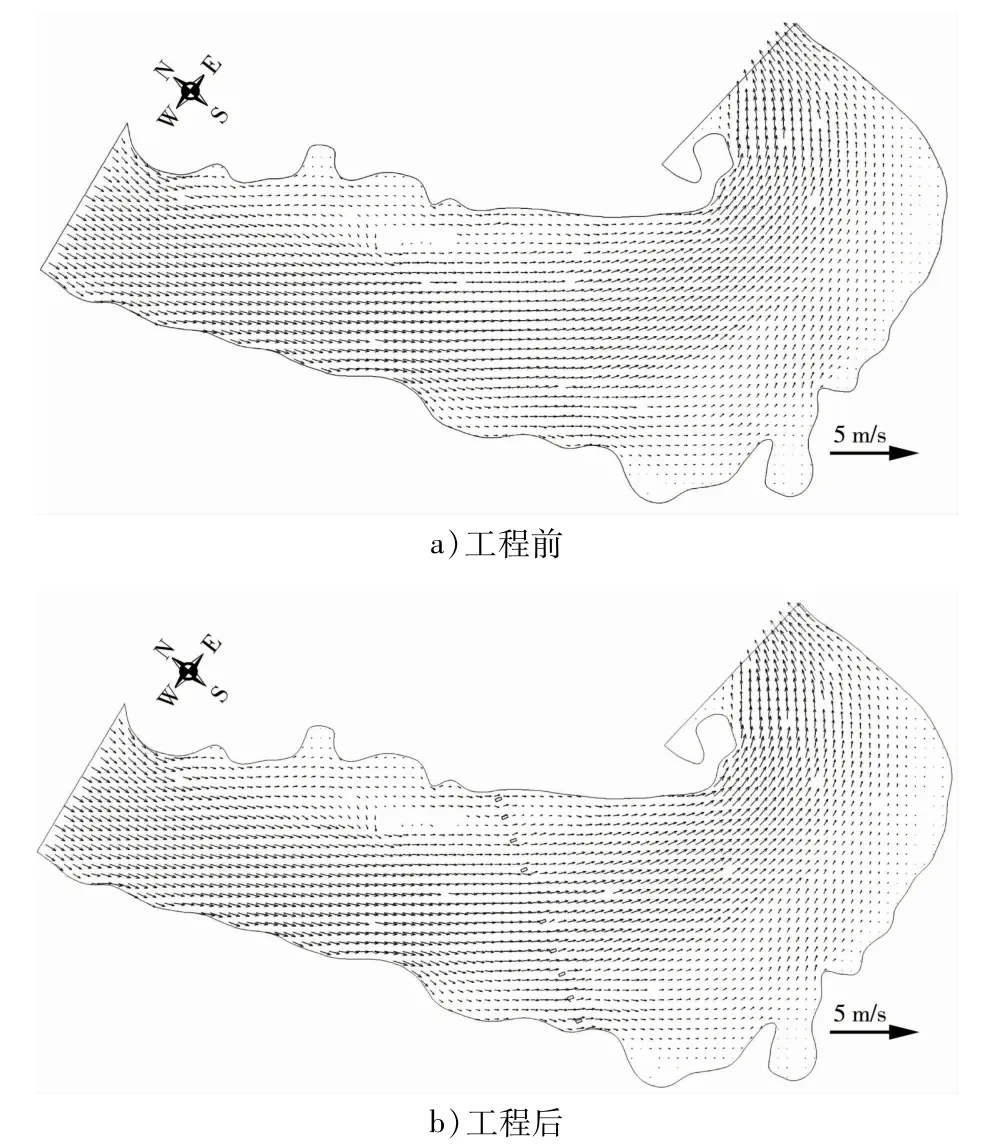
圖7 洪水流場

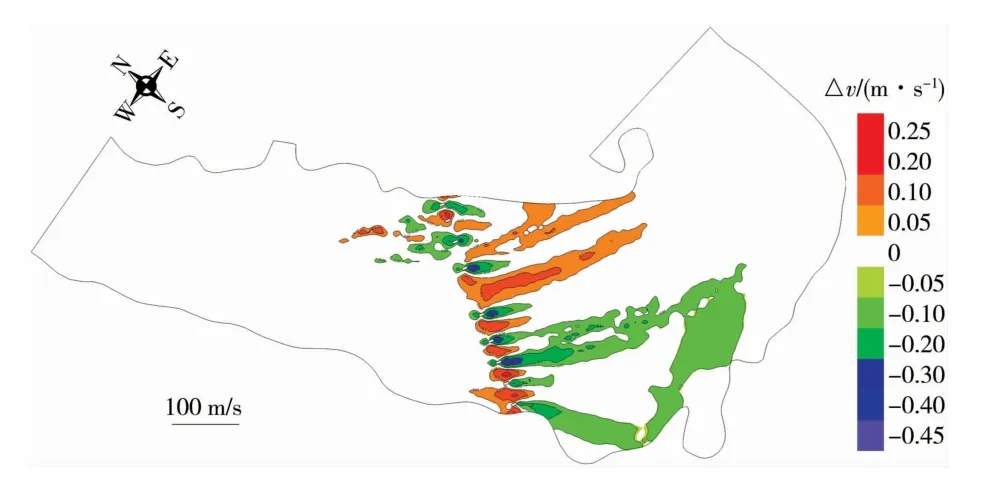
圖8 洪水流速變化等值線

工程實施后，橋附近流速會發生一定的變化。在各頻率洪水條件下時，橋墩所在位置流速減小，而橋墩間的流速有所增加。 工程前后流速變化的等值線分布趨勢為以橋墩所在位置為起點，呈細長的舌狀，于河道流線方向延伸，整體上距離橋梁斷面越近，流速變化越大。 右岸區域流速減小范圍較大，由于擬建斜交橋的橋墩布置與水流方向形成夾角所致。 但由于擬建橋梁橋墩較小，橋墩對河道流速流態的影響僅局限在橋址附近。 工程建成后，受橋墩阻水作用影響，從流速影響范圍來看，其影響超過0.05 m/s的最大范圍在橋位上游180 m至橋位下游320 m以內。 流速一般變化規律為“橋墩之間增加，橋墩與河岸之間增加，橋墩上、下游附近減小”。

3.3 工程對河勢變化的影響

擬建橋梁工程使局部河段的水位和流速特征發生變化，從而引起河道挾沙力發生改變，而泥沙輸移規律的改變會使河床沖淤變化引起相應的河勢調整。 因此，擬建工程導致河床的沖淤變化可以從工程前后河道挾沙力變化率進行分析，見式(3)。

式中 S——挾沙力變化率；C0、C1——工程前和工程后質量含沙量。

質量含沙量C的算式可根據渾水潛流動量方程推導得出，表示為:

式中 CD——阻力系數；ρ、ρs——水、泥沙的密度；V——流速；α——常數；ω——泥沙沉速。

假設工程后上游來水來沙不變，加上建橋后工程河段流速和水深變化不大，故認為研究區域建橋前后CD、α和ω相同。 圖9 為建橋前后研究區域挾沙力變化率S 分布。

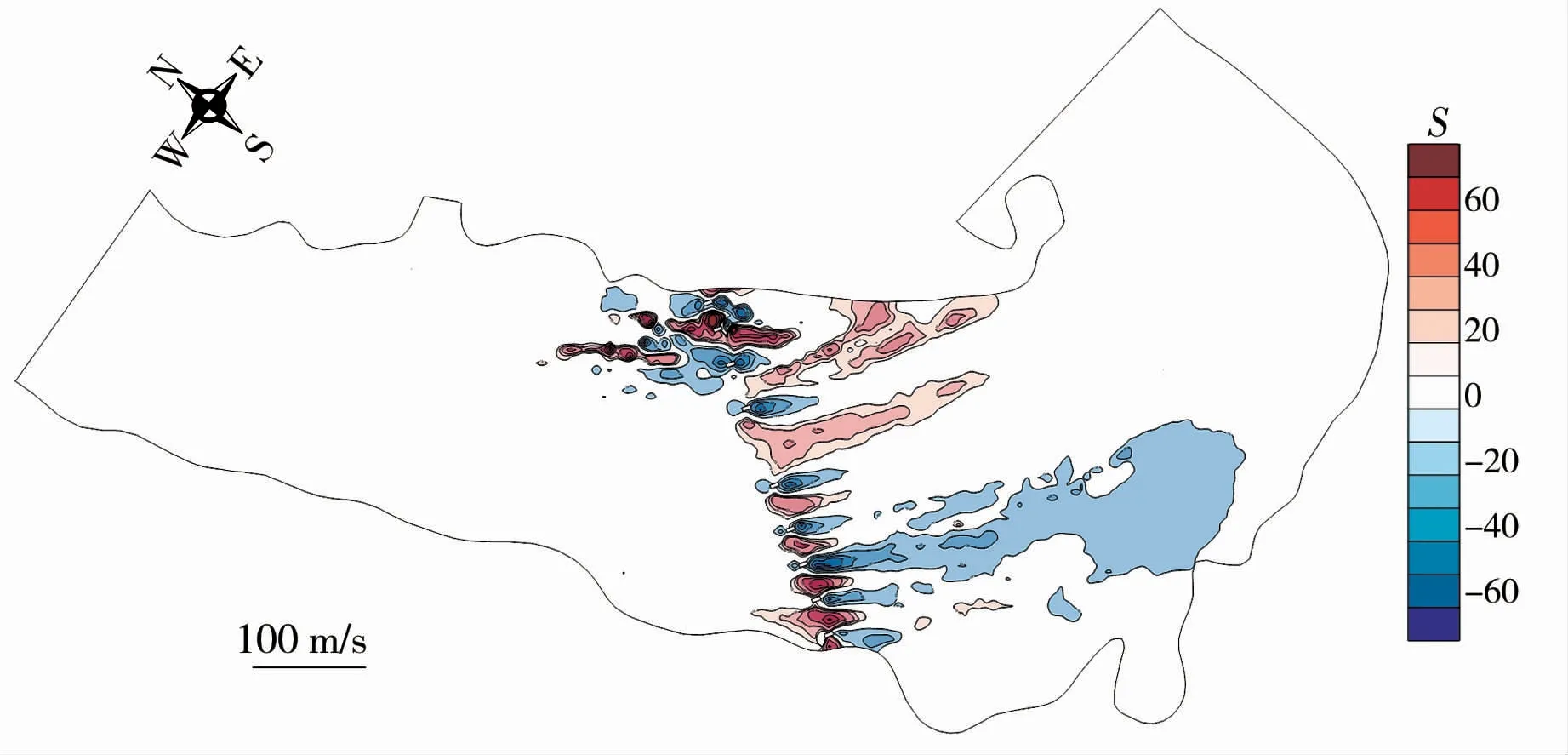
圖9 建橋導致的挾沙力變化

在上游來水來沙一定時，工程段河勢演變規律受到水深和流速變化的影響。 而從工程前后流速和水深變化來看，工程對河勢的影響在上下游有限的區間內，主要集中在橋梁下游，橋墩間沖刷按照公路橋位設計中的河槽一般沖刷公式(64 -2 簡化式)[16]計算，結合地質條件，大橋建設造成河道最大沖刷深度為1.8 m。 圖9 所示，挾沙力增加區域位于橋墩之間流速增加區域，影響的最大范圍距橋墩約250 m；挾沙力減小區域主要位于橋梁至下游350 m范圍內的凹岸一側，所以工程建設不會加劇橋位下游凹側河段的沖刷。

4 結論

本次采用有限體積法，結合非結構網格，通過實測地形數據，建立斜交橋所在彎道河段水動力學模型，經驗證該模型模擬結果基本合理，可應用于該區域的水流特征研究。

利用構建的數學模型模擬分析了P=10%和P=20% 2種洪水條件下擬建大橋對河道水位、流速及河勢變化的影響，結果表明大橋建設對河道水位、流速和流態的影響范圍較小，影響有限。 同時由于橋墩與水流方向呈現出一定的夾角，使得橋位下游凹岸流速和挾沙力較工程前有所減少，凸側流速和挾沙力較工程前有所增加，工程建設不會加劇下游凹側河段的沖刷，橋墩間最大沖刷深度為1.8 m。