基于滲流的改進雙強度折減法邊坡穩定性分析

周錦濤，肖博文，蔣鵬飛，王雪蓉，黃耀興

(1.三峽大學水利與環境學院，湖北 宜昌 443000；2.襄陽市南漳縣東鞏鎮人民政府，湖北 襄陽 441528；3.長江三峽通航管理局，湖北 宜昌 443002 )

邊坡失穩是工程中常見的問題，嚴重影響工程安全，而滲流在影響邊坡穩定性的因素中占據重要地位，所以在考慮滲流應力耦合作用下如何對邊坡的穩定性進行分析是一個十分重要的問題[1]。 近年來，數值模擬計算滲流場應力場耦合狀況下邊坡的穩定性成為一種主流[2-3]。 盧玉林等[4]在滲流應力雙向耦合的基礎上探討了兩級邊坡滲流耦合破壞的機理。 田杰[5]通過比奧理論研究了滲流應力耦合作用下邊坡穩定性。 童富果等[6]通過入滲控制方程的求解計算，實現了滲流場應力場耦合的直接求解。 張仁成等[7]利用水力全耦合分析模型，研究了滲流作用下邊坡的位移分布和破壞形式。 這些研究成果在改進滲流耦合模型、強度折減方式方面取得很大進展，但在安全系數的計算方法和安全性上仍有待提高。 本文在考慮滲流應力耦合的情況下采用了改進的雙強度折減法，改進了安全系數的計算方式，提高了安全性；通過案例發現，自然工況下，改進的雙強度折減法計算結果較傳統單強度折減法更安全。 暴雨工況下滲流對邊坡安全系數影響比較明顯。 因此在考慮滲流影響的條件下采用改進的雙強度折減法對邊坡進行分析可以得到更符合實際的結果，為實際工程安全提供參考。

1 改進雙強度折減法

式中 c、φ——邊坡原始黏聚力和內摩擦角，c′、φ′——進行雙強度折減后邊坡臨界狀態時的黏聚力和內摩擦角。

邊坡失穩過程的實質是邊坡的材料強度參數不斷的弱化衰減，假設邊坡折減比一定時，其臨界狀態的強度與邊坡初始強度無關，邊坡臨界參數不會隨著初始強度參數的改變而發生改變。 因此本文提供一種新的雙折減安全系數計算方式。 以內摩擦角和黏聚力作為橫縱坐標建立直角坐標系(圖1)。

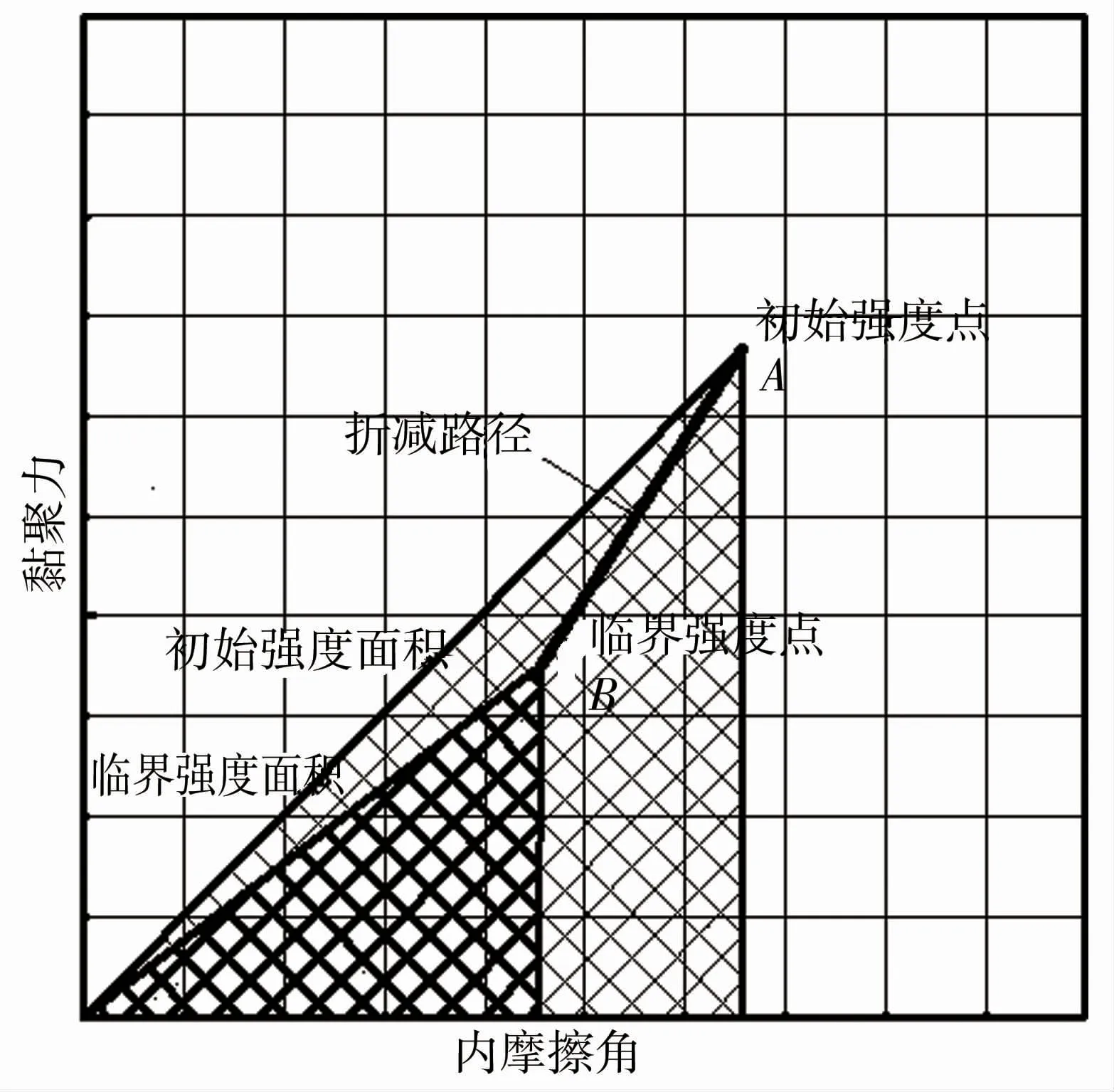
圖1 強度坐標系三角形強度面積

A點為邊坡的初始強度參數點，其坐標表示初始狀態下邊坡的黏聚力和內摩擦角，此時與坐標軸圍成的三角形面積S1稱之為“初始強度面積”；B點為邊坡臨界強度參數點，所對應的三角形的面積S2稱為“臨界強度面積”，計算見式(3)、(4)。

S1與S2大小并不代表邊坡的強度值的大小，在雙強度折減的計算過程中，邊坡的強度是通過黏聚力c和內摩擦角φ的折減完成的，而強度面積的定義是直角坐標系的特性，所以可以利用三角形面積去表示雙折減過程中強度的變化。

當折減比k=1 時，內摩擦角折減系數SRF1和黏聚力折減系數SRF2在臨界狀態的取值見式(5):

式(5)可以等價變換為式(6):

當折減比k≠1 時，在強度參數坐標系中，分子表示初始強度參數點、坐標原點(0，0)、橫坐標軸所圍成的三角形面積，稱為“初始強度面積”，那么同理分母表示臨界狀態點、坐標原點(0，0)、橫坐標軸所圍成的三角形面積稱為“臨界強度面積”，見圖1，因此，式(6)又可以表示為式(7):

由此可以得到通過“強度面積”推出的強度雙折減的關系為式(8):

式中 SRF1——單獨對內摩擦角φ單獨進行折減時的折減系數SRFφ；SRF2——單獨對黏聚力c進行折減時的折減系數SRFc。

其適用范圍為折減比k∈ [0.6，1.4 ]。 此時在直角坐標系中初始強度點與臨界強度點之間連線的斜率就是采用不同強度折減比。

2 滲流場和應力場耦合

通過對滲流場和應力場的分析，得到穩定滲流場與應力場耦合分析的連續介質模型[12]。

a)應力場影響下的滲流場數學模型。

c)滲流-應力耦合有限元基本方程。 將滲流場數學模型和應力場數學模型組合起來[13-14]，得到如下雙場耦合有限元模型:

式中 [ ]K——與滲透系數有關的矩陣；[ ]F——與滲透坡降有關的滲透力矩矩陣；[ ]M ——整體剛度矩陣；{ }f——水頭分布函數。

若給定邊界條件和初始條件，上述雙場耦合模型便可通過數值模擬確定耦合效應。 為了更好地把握耦合整體方程的收斂性，本文采用間接耦合的方式對滲流場應力場耦合進行計算。 考慮到上述公式求解比較困難，故用ANSYS 進行滲流計算[15-16]。

3案例分析

3.1 邊坡模型的建立

蔣家淌滑坡位于湖北省興山縣大禮溪左岸蔣家趟村，滑坡后緣出現陡坎，高度15 ～18 m，滑體最大水平位移35 m，垂直位移16 m。 選取一個典型坡面建立模型，剖面形式及巖性見圖2，各巖土層力學參數見表1。 模型力學邊界條件為:底部邊界為固定約束，X、Y方向的可變位移為0，左右邊界施加水平方向約束，X方向水平位移為0。 滲流邊界條件為:底部與左右兩側設置為不透水邊界，上部設為透水邊界；失穩判據采用特征點位移突變結合塑性區貫通來確定邊坡的安全系數。

表1 巖土物理力學參數

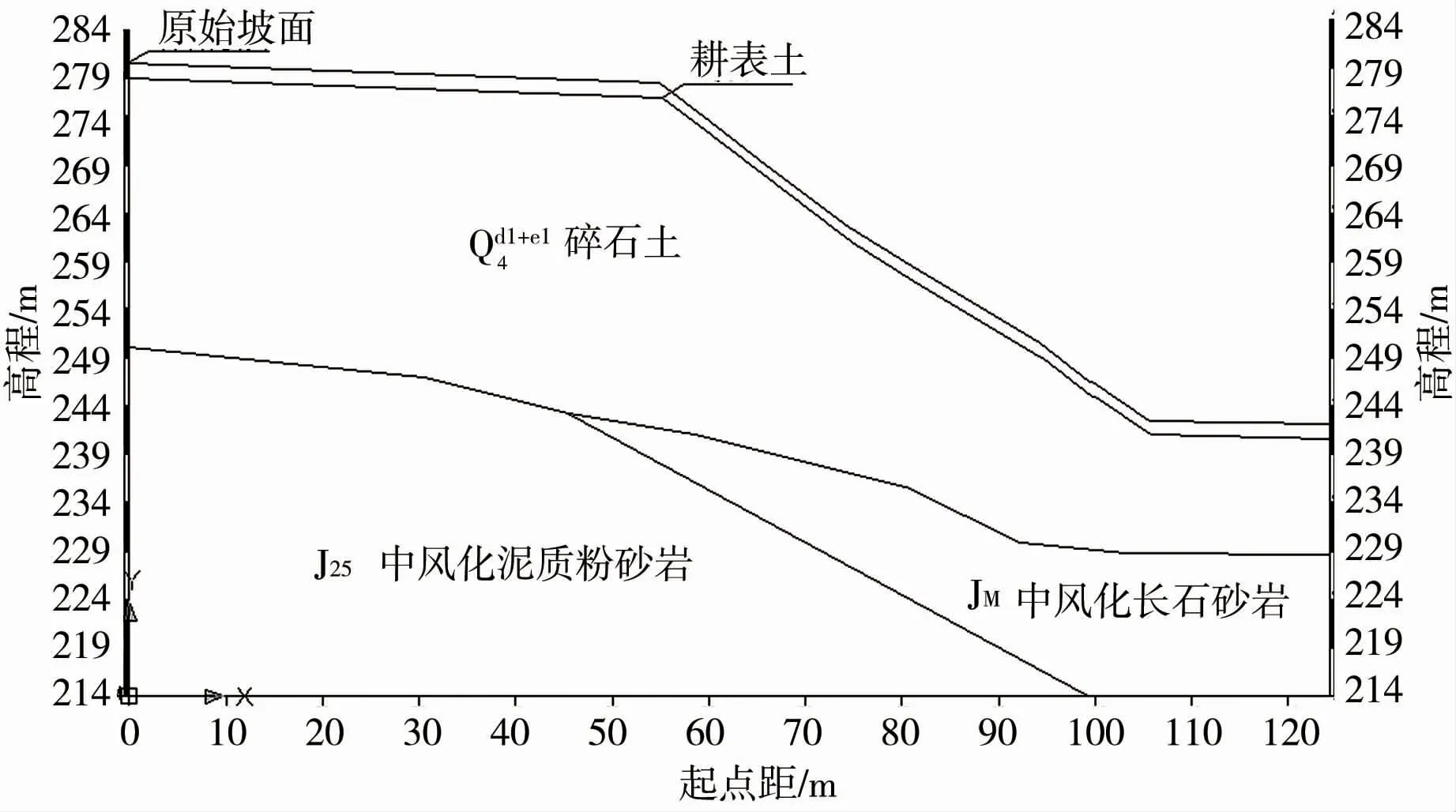
圖2 典型坡面截面巖性示意

3.2 自然工況下單強度折減法邊坡穩定性分析

通過對邊坡算例進行分析，得到安全系數與水平最大位移關系和塑性區貫通時的塑性云圖，見圖3、4。 圖中可見，在安全系數為1.37 和1.40 時水平最大位移發生突變。 在安全系數為1.40 時塑性區貫通，故該邊坡在采用單強度折減法時，安全系數為1.40。

圖3 單強度折減安全系數與最大水平位移關系

圖4 Fos=1.40 時邊坡塑性區云圖

3.3 自然工況下改進雙強度折減邊坡穩定性分析

為使誤差減小，折減比范圍取k∈ [0.8，1.0 )，分別對k等于0.8、0.9 時進行計算。 通過ANSYS和式(1)—(3)得到的具體計算結果，見表2。

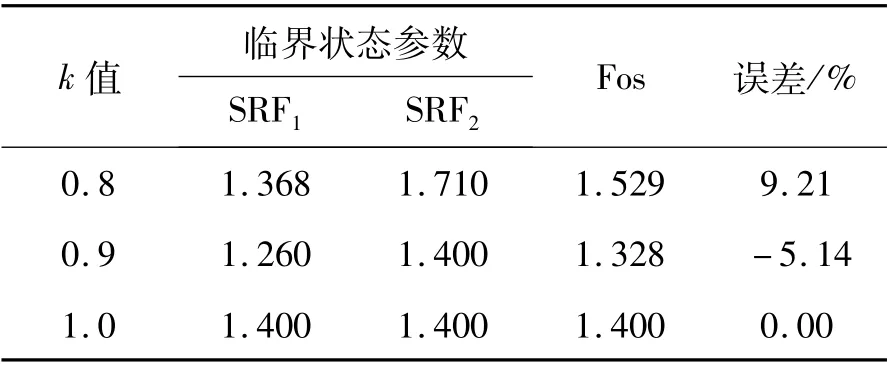
表2 自然狀態下不同折減比下邊坡安全系數及誤差

當k=0.8 時，安全系數與水平最大位移關系和塑性云圖見圖5、6。 由圖可知當位移發生突變且塑性區貫通時，安全系數為1.529。 當k=0.9 時，安全系數與最大水平位移關系和塑性云圖見圖7、8。由圖可知當位移發生突變且塑性區貫通時，安全系數為1.328。

圖5 強度折減安全系數與最大水平位移關系(k=0.8)

圖6 Fos=1.529 時邊坡塑性區云圖

圖7 強度折減安全系數與最大水平位移關系(k=0.9)

圖8 Fos=1.328 時邊坡塑性區云圖

通過表2 可知，當k取0.8 時，安全系數計算偏差絕對值為9.21%；當k取0.9 時安全系數計算偏差絕對值為5.14%，故折減比取0.9 較為合適，此時安全系數為1.328。

3.4 暴雨工況下滲流應力耦合雙強度折減邊坡穩定性分析

根據參數條件，通過ANSYS 熱分析模塊計算出邊坡孔隙水壓力值，見圖9；采用間接耦合的方法對滲流場與應力場進行耦合，用改進強度雙強度折減法對邊坡進行計算。

圖9 孔隙水壓力等值線

折減比取為0.9 時，安全系數與最大位移關系和塑性云圖，見圖10、11，圖中可見在安全系數為0.97 時位移發生突變，同時塑性區貫通，故考慮滲流時邊坡安全系數為0.97。

圖10 強度折減安全系數與最大水平位移關系(k=0.9)

圖11 Fos=0.97 時邊坡塑性區云圖

3.5 結果對比

對比3 種計算結果，見表3。 自然工況下，改進雙強度折減法計算出的安全系數為1.328，傳統單強度折減法計算出的安全系數為1.400，誤差絕對值為5.42%，說明該方法計算安全系數是可行的；暴雨工況下，即考慮滲流的情況下，改進雙強度折減法計算出的安全系數為0.97，滲流應力耦合情況下安全系數較自然工況降低了27%，可知滲流對邊坡的穩定性有顯著影響。

表3 不同折減方式下邊坡安全系數

4 結論

a)采用改進雙強度折減法對邊坡進行分析，改善了傳統單強度折減法中因為黏聚力c與內摩擦角φ按相同的折減速度進行折減從而掩蓋c與φ在保持坡體穩定性中發揮著不同作用的問題。

b)對邊坡進行了2 種工況，3 種計算方式的分析，發現折減比k的范圍在 [0.8，1.0 )較為合適，結果表明取0.9 最為合理，極大程度地減少了試算過程中的工作量，提高了安全系數的計算效率。

c)相同工況下，采用改進雙強度折減法對邊坡進行分析時所得結果較傳統單強度折減法降低了5.42%，說明該方法計算安全系數是可行的，并且更安全。

d)滲流對邊坡的穩定性影響比較明顯，達到了27.00%，在邊坡失穩過程中，不同的水荷載分布對應著相應的滲流場分布，滲流場改變了巖土介質中水荷載分布進而改變了應力場，因此在進行邊坡的穩定性分析中不可忽略滲流應力的影響。 即邊坡在自然情況下處于安全狀態，當考慮滲流影響時仍可能發生失穩，所以本文采用的考慮滲流的改進雙強度折減法可以得到更符合實際的結果，為實際工程提供參考。