基于擴(kuò)展概念格的帶約束關(guān)聯(lián)分類規(guī)則挖掘方法
翟悅,李楠,于文武
(1.大連科技學(xué)院 數(shù)字技術(shù)學(xué)院,遼寧 大連116052;2.大連交通大學(xué) 軟件學(xué)院,遼寧 大連 116028) *
近年來(lái)采用關(guān)聯(lián)規(guī)則構(gòu)造分類器的關(guān)聯(lián)分類方法廣泛應(yīng)用于醫(yī)療、社會(huì)服務(wù)等領(lǐng)域,然而產(chǎn)生的關(guān)聯(lián)分類規(guī)則CARs(Class Association Rules)往往會(huì)包含大量冗余規(guī)則,對(duì)此許多學(xué)者展開了帶約束的關(guān)聯(lián)分類算法研究,該類算法主要分為事前處理與事后處理兩種策略,采用約束事前處理方法如: CBC[1]、FP-growth[2],這類算法當(dāng)用戶關(guān)心的約束條件變化后,算法不得不重新掃描數(shù)據(jù)庫(kù),根據(jù)新約束集重新構(gòu)建分類器,不具備重用性;采用約束事后處理方法如: CCAR[3]、MAC[4]等方法. 該類算法會(huì)產(chǎn)生大量候選CARs從而降低算法性能.
本文采用約束事后處理方法,為解決產(chǎn)生候選項(xiàng)目集過多導(dǎo)致效率低下等問題:本文利用擴(kuò)展概念格結(jié)構(gòu)存儲(chǔ)頻繁項(xiàng)目集FIs (Frequent Itemsets),運(yùn)用結(jié)點(diǎn)之間關(guān)系定理快速在概念格中搜索符合約束條件的CARs;格結(jié)點(diǎn)在信息不丟失的前提條件下大大減少形成分類規(guī)則的數(shù)量,差集(diffset)概念引入不僅降低格結(jié)點(diǎn)內(nèi)存占用,還能加快對(duì)類屬性支持度和置信度計(jì)算,使得改進(jìn)后的挖掘算法在時(shí)間和空間上具備良好性能.當(dāng)約束條件變化時(shí)無(wú)需重新建立概念格,僅需在格上重新搜索.
1 基本定義
1.1 關(guān)聯(lián)分類規(guī)則相關(guān)概念
設(shè)數(shù)據(jù)庫(kù)D=(AEC),其中:一個(gè)項(xiàng)目集合由條件屬性A={A1,A2,…,An}構(gòu)成,每一個(gè)條件屬性Ai可以取某一個(gè)特定的值,項(xiàng)目集X={(Ai1,ai1), (Ai2,ai2),…,(Ain,ain)},類屬性C={c1,c2,…,ck}.見表1.

表1 范例數(shù)據(jù)庫(kù)D
定義1關(guān)聯(lián)分類規(guī)則R形如蘊(yùn)含式:X→Cj,其中Cj∈C,X為項(xiàng)目集[5]
例如:a3→Y即為一條關(guān)聯(lián)分類規(guī)則.
定義2在數(shù)據(jù)庫(kù)D中包含項(xiàng)目集X記錄集合 記 為 Oidset(X).發(fā) 生 數(shù) ActOcc(X) 定 義 為
|Oidset(X)|[6].
例如:Oidset (a3)={4,5,6}.ActOcc (a3)= |Oidset (a3)|=|{4,5,6}|=3.
定義3關(guān)聯(lián)分類規(guī)則R的支持?jǐn)?shù)Sup(R)定義為:滿足規(guī)則的條件屬性同時(shí)滿足類屬性記錄數(shù)目[7].
例如:Sup(a3→Y)=|{4,6}|=2.
定義4關(guān)聯(lián)分類規(guī)則R置信度定義為:Conf(R) =Sup(R)/ ActOcc (R)[7].
例如:Conf(a3→Y)= Sup(a3→Y)/ ActOcc (a3) = |{4,6}|/|{4,5,6}|=2/3.
1.2 約束條件
在數(shù)據(jù)挖掘中常使用的約束類型分為:知識(shí)約束、數(shù)據(jù)約束、層次約束、規(guī)則約束、興趣度約束等.本文研究數(shù)據(jù)約束,允許用戶根據(jù)關(guān)注目標(biāo)在規(guī)則挖掘過程中加入項(xiàng)目集約束條件,即僅挖掘包含某些項(xiàng)目的規(guī)則,使得規(guī)則挖掘過程更具效用.
定義5設(shè)β為項(xiàng)目集約束條件集,β={X1,X2, …,Xn},其中每個(gè)Xi形如ii1∧ii2∧ii3∧……∧ii2∧iik∈I,I={i1,i2,…,im}是m個(gè)不同項(xiàng)目的一個(gè)集合.
定義6滿足約束條件集β的關(guān)聯(lián)分類規(guī)則R=X→Cj必須滿足:iff?Xi?β,且Xi?X[8].
例如: 假設(shè)約束集β={<(A,a3),(B,b3)>,
2 擴(kuò)展概念格結(jié)構(gòu)
2.1 結(jié)點(diǎn)結(jié)構(gòu)與格定義
定義7設(shè)T與W為k-項(xiàng)集,它們共同擁有相同 (k-1)-項(xiàng)集作為前綴,由T直接生成其孩子結(jié)點(diǎn)(k+1)-項(xiàng)集記為:childrenEC(T)={TX|TX∈(k+1)-項(xiàng)集,且X屬于W后項(xiàng)}[9].
定義8設(shè)T為k-項(xiàng)集,由T間接生成孩子結(jié)點(diǎn)(k+1)-項(xiàng)集記為:childrenL(T)={Y|Y∈(k+1)-項(xiàng)集,T?Y,Y?childrenEC(T)}[9].
例如:圖1所示,其中由T直接生成的孩子結(jié)點(diǎn)childrenEC(T)均表示為實(shí)線,由T間接生成的孩子結(jié)點(diǎn)childrenL(T)均表示為虛線.假設(shè)T為bc,根據(jù)定義7由T直接生成的(k+1)-項(xiàng)集childrenEC(bc) ={bcd},根據(jù)定義8由T間接
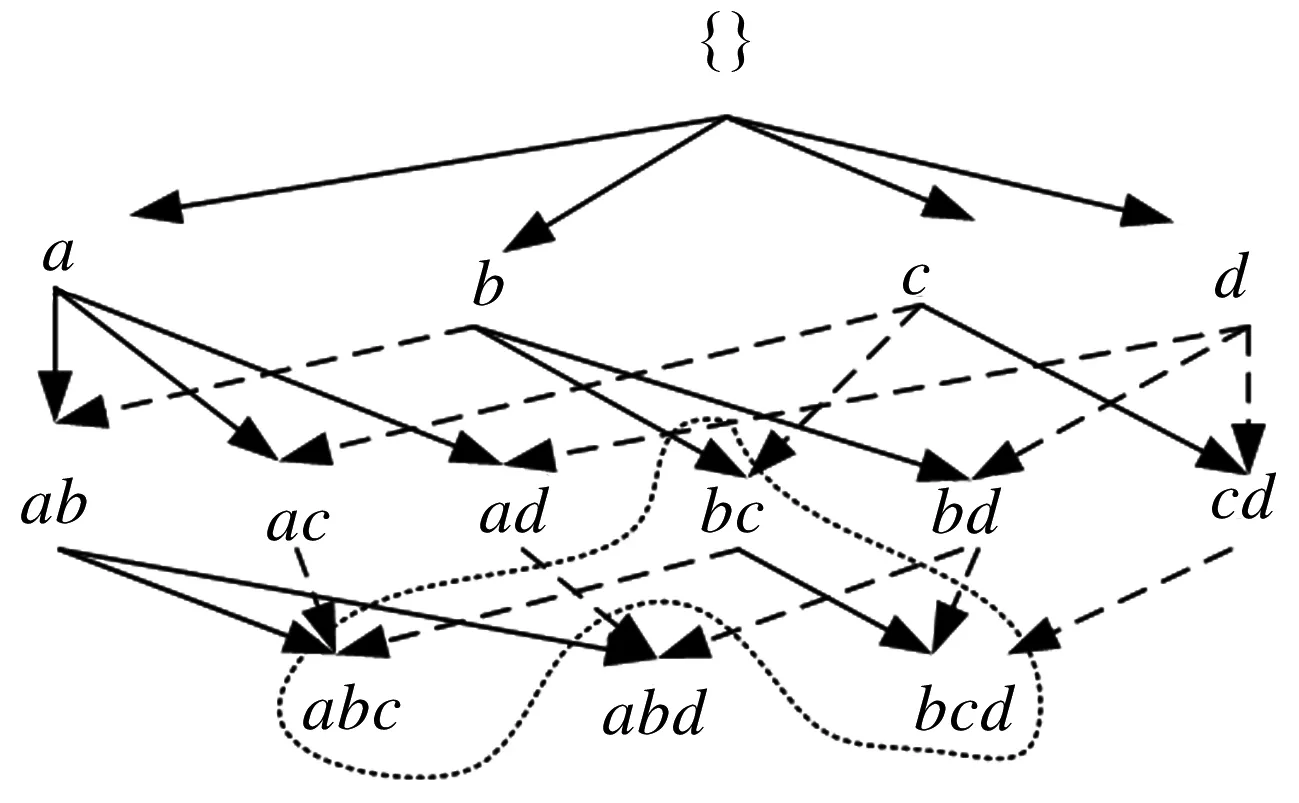
圖1 概念格結(jié)點(diǎn)鏈接過程
生成的孩子結(jié)點(diǎn)childrenL(bc)={abc}.定義9擴(kuò)展概念格第一層結(jié)點(diǎn)定義為五元組Node
(1)id為存儲(chǔ)結(jié)點(diǎn)id,根據(jù)該項(xiàng)目集所包含屬性二進(jìn)制表示.
(2)atts屬性集為頻繁1-項(xiàng)集.
(3)Oidset(o1,o2,…om)記錄集為包含(2)中屬性集atts在每個(gè)類屬性中的集合.
(4)countL(c1,c2,…ck)為統(tǒng)計(jì)(3)中記錄集在每一個(gè)類屬性中的數(shù)目ci=|oi|.
(5)pos為maxi∈[1,j]{Ci},如果每個(gè)分類的統(tǒng)計(jì)值相等,則pos默認(rèn)為C1.
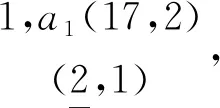
2.2 差集概念diffset
差集概念首先由Zaki等人[10]在2003年提出,本文將差集引入關(guān)聯(lián)分類規(guī)則挖掘,在擴(kuò)展概念格高層的結(jié)點(diǎn)所存儲(chǔ)信息中,使用差集替代定義9中Oidset,可有效減少格中結(jié)點(diǎn)所占用存儲(chǔ)空間,還能利用差集快速計(jì)算類屬性的支持?jǐn)?shù)和置信度.
定義10假設(shè)兩個(gè)項(xiàng)目集PX與PY均以P為前綴的等價(jià)類,d(PXY)= Oidset (PX)- Oidset (PY)[11].
定理1已知兩個(gè)項(xiàng)目集PX、PY與d(PX)、d(PY),可證明d(PXY)=d(PX) -d(PY).
證明:因?yàn)閐(PXY)= Oidset (PX)-Oidset (PY)=Oidset(PX)-Oidset(PY)+Oidset(P)-Oidset(P)=(Oidset (P)-Oidset(PY))- (Oidset(P)- Oidset(PX))=d(PY)-d(PX).差集計(jì)算示意如圖2所示.
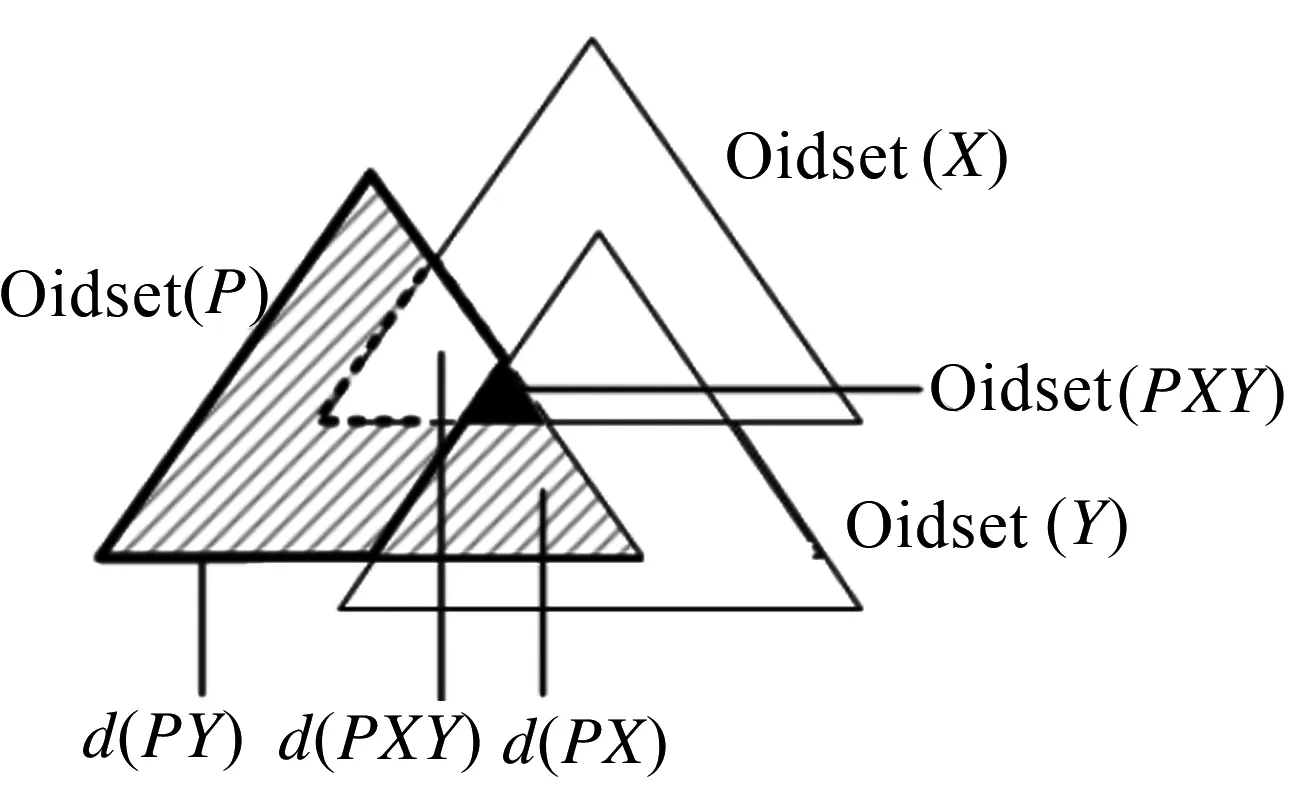
圖2 差集計(jì)算過程
定義11擴(kuò)展概念格高層次的結(jié)點(diǎn)定義為五元組Node(id, atts, diffset(d1,d2,…dk), countL(c1,c2,…ck) ,pos)表示,其中:
(1) diffset(d1,d2,…,dk)為對(duì)應(yīng)記錄集oi的差集.
(2)countL(c1,c2,…,ck)為計(jì)算方法公式ci=X.ci- |diffseti|.
(3) 其他結(jié)點(diǎn)信息與定義9一致.
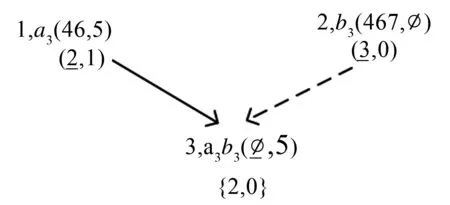
圖3 擴(kuò)展概念格結(jié)點(diǎn)鏈接舉例
3 擴(kuò)展概念格構(gòu)建方法
3.1 相關(guān)定理
定理2已知兩個(gè)概念格中結(jié)點(diǎn)X、Y,如果兩個(gè)結(jié)點(diǎn)具有相同的條件屬性,且屬性值不相等,則Oidset(X)∩Oidset(Y)=?.
定理3已知概念格中兩個(gè)結(jié)點(diǎn)XA、XB,如果?XB∈childrenEC(X),且XA結(jié)點(diǎn)先與XB生成,則?Y∈childrenEC(XB)∪children(XB),使得Y∈children(XA).
定理3說(shuō)明擴(kuò)展概念格中childrenL(XA)間接孩子結(jié)點(diǎn)確定時(shí)僅需搜索滿足如下條件的結(jié)點(diǎn),條件1:Y∈children(X);條件2:YZ∈childrenEC(Y);條件3:判斷如果XA?YZ,那么YZ∈children(XA).運(yùn)用定理3削減了大量候選項(xiàng)目集結(jié)點(diǎn).
3.2 基于差集的擴(kuò)展概念格構(gòu)建算法
本文提供一種基于差集的擴(kuò)展概念格結(jié)構(gòu)LD (Lattice basedDiffset),該結(jié)構(gòu)包含全部的頻繁項(xiàng)目集信息.基于差集的擴(kuò)展概念格LD生成算法Build_LD步驟如下:
步驟1:輸入數(shù)據(jù)庫(kù)D,初始化最小支持度minsup;初始化擴(kuò)展概念格Li←?;
步驟2:搜索數(shù)據(jù)庫(kù)D生成滿足minsup的頻繁1-項(xiàng)集,調(diào)用概念格更新算法構(gòu)建Lr,生成擴(kuò)展概念格第1層結(jié)點(diǎn);
步驟3:進(jìn)行格結(jié)點(diǎn)鏈接操作,根據(jù)定理2,如果lx.id≠ly.id,使用lx.Oidset∪ly.Oidset計(jì)算格中結(jié)點(diǎn)的記錄集;
步驟4:根據(jù)定義9和定理1,如果lx為概念格第2層結(jié)點(diǎn),使用Oidset(lx) -Oidset(ly)計(jì)算格結(jié)點(diǎn)差集,如果lx為高層次結(jié)點(diǎn),使用ly.diffseti-lx.diffseti計(jì)算格結(jié)點(diǎn)差集;
步驟5:統(tǒng)計(jì)步驟3中記錄集在每一個(gè)類屬性中的數(shù)目ci=|oi|.計(jì)算pos并標(biāo)記;
步驟 6:如果pos≥minsup,則調(diào)用概念格更新算法,更新lx.childrenEC和ly.childrenL,轉(zhuǎn)步驟3;
3.3 基于差集的擴(kuò)展概念格構(gòu)建實(shí)例
首先針對(duì)表1所示數(shù)據(jù)庫(kù)D(minsup=25%),利用Build_LD算法產(chǎn)生的擴(kuò)展概念格結(jié)構(gòu)見圖4.擴(kuò)展概念格LD根結(jié)點(diǎn)為空結(jié)點(diǎn),調(diào)用Build_LD算法生成擴(kuò)展概念格第一層結(jié)點(diǎn)為〈{a1},{a2},{a3},{b1}, {b2}, {b3},{c1},{c2}〉,其中{b1}結(jié)點(diǎn)2,b1(1,5)(1,1)不滿足最小支持度minsup要求,故LD中不產(chǎn)生該結(jié)點(diǎn).此后根據(jù)定義11和定理2生成第二層結(jié)點(diǎn),分別為〈{a1b2},{a1b3},{a1c1},{a1c2},{a2b2},{a2b3},{a2c1},{a2c2},{a3b2},{a3b3},{a3c1},{a3c2},{b2c1},{b2c2},{b3c1},{b3c2}〉.其中僅有〈{a2b2}, {a3b3},{a3c1},{b2c1},{b3c1}〉五個(gè)結(jié)點(diǎn)滿足最小支持度minsup要求.如圖5(a)所示,計(jì)算結(jié)點(diǎn)3,a3b2(46,5)(0,0)不滿足minsup要求,不產(chǎn)生該結(jié)點(diǎn).由算法Build_LD可知,生成概念格二層結(jié)點(diǎn)差集計(jì)算公式為O.diffseti= Oidset(lx) -Oidset(ly),而在計(jì)算高層概念格結(jié)點(diǎn)差集計(jì)算公式為O.diffseti=ly.diffseti-lx.diffseti.如圖5(b)所示.
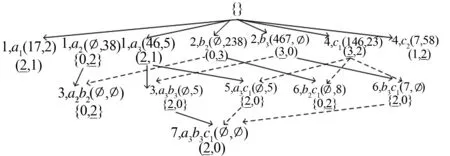
圖4 表1構(gòu)建擴(kuò)展概念格結(jié)構(gòu)

圖5 擴(kuò)展概念格二層結(jié)點(diǎn)與高層結(jié)點(diǎn)計(jì)算過程
圖4展示出算法1的執(zhí)行過程,可以看出根據(jù)算法Build_LD構(gòu)建基于差集的擴(kuò)展概念格有效縮減了結(jié)點(diǎn)數(shù)目,F(xiàn)Is又在不丟失有效信息的前提下降低了建造整個(gè)格的復(fù)雜度.差集的運(yùn)用進(jìn)一步節(jié)省了存儲(chǔ)空間和計(jì)算時(shí)間.
4 帶約束關(guān)聯(lián)分類規(guī)則提取
在約束型關(guān)聯(lián)分類規(guī)則挖掘過程中,約束條件會(huì)隨著實(shí)際應(yīng)用場(chǎng)景中用戶需求而不斷變化,本文提出規(guī)則提取算法是在構(gòu)建的擴(kuò)展概念格結(jié)構(gòu)上進(jìn)行挖掘,LD結(jié)構(gòu)本身包含頻繁項(xiàng)目集完整信息,以便于當(dāng)約束條件改變,僅需按照新約束條件在LD中重新搜索且無(wú)需重復(fù)構(gòu)建格,從而加快挖掘速度.
4.1 帶約束的關(guān)聯(lián)分類規(guī)則提取算法LD-CAR
在帶項(xiàng)目集約束下,本文提供一種基于差集的概念格提取關(guān)聯(lián)分類規(guī)則方法LD-CAR (Diffset and Lattice based algorithm for CAR mining),該算法挖掘步驟如下:首先根據(jù)算法Build_LD建立完成的基于差集的概念格結(jié)構(gòu),遍歷概念格LD,根據(jù)用戶給定約束集生成符合條件的CARs,并為符合約束結(jié)點(diǎn)做flag標(biāo)記;然后算法清空結(jié)點(diǎn)flag標(biāo)記以備下次利用新約束進(jìn)行掃描.帶約束的關(guān)聯(lián)分類規(guī)則提取算法Find_CARs步驟如下:
步驟1:輸入LD,初始化約束條件集β,最小置信度minconf;
步驟2:遍歷LD中結(jié)點(diǎn),對(duì)于每個(gè)itemseti∈β,搜索LD尋找包含itemseti的結(jié)點(diǎn)li;
步驟3:判斷如果ifl.flag=false且conf≥minconf,則將該規(guī)則并入CARs中,CARs←CARs∪{l.itemset→cpos},設(shè)置l.flag=true;
步驟4:遞歸調(diào)用遍歷LD中結(jié)點(diǎn)方法;
步驟5:輸出滿足約束條件集β的關(guān)聯(lián)分類規(guī)則;
步驟6:重置LD結(jié)點(diǎn)的flag=false,以 便給定下一組新的約束條件下繼續(xù)生成CARs.
4.2 帶約束的關(guān)聯(lián)分類規(guī)則提取實(shí)例
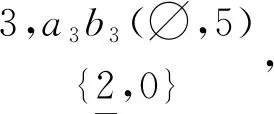
Ruler1:
Ruler2:
Ruler3:
Ruler4:
Ruler5:
Ruler6:
Find_CARs算法挖掘出的關(guān)聯(lián)分類規(guī)則集是滿足約束添加下的不重復(fù)完備規(guī)則集.在Find_CARs算法最后一步將全部結(jié)點(diǎn)flag標(biāo)簽重置以備下一組新約束集的挖掘.
5 實(shí)驗(yàn)結(jié)果
為了進(jìn)一步驗(yàn)證算法的有效性,實(shí)驗(yàn)主要比較本文算法LD-CAR、文獻(xiàn)3所提到的CCAR算法和文獻(xiàn)4提出的MAC算法3者之間的性能差異.測(cè)試的硬件平臺(tái)為:Intel Core i5-6200 CPU 2.4GHz,內(nèi)存8GB,操作系統(tǒng)Windows10,使用C#在Visual studio2013運(yùn)行環(huán)境中實(shí)現(xiàn)三種算法,測(cè)試數(shù)據(jù)集來(lái)自http://fimi. uantwerpen.be/data/.如表2所示選取3個(gè)不同特點(diǎn)的數(shù)據(jù)庫(kù)進(jìn)行關(guān)聯(lián)分類規(guī)則挖掘性能實(shí)驗(yàn).

表2 實(shí)驗(yàn)數(shù)據(jù)庫(kù)特征
5.1 挖掘時(shí)間
實(shí)驗(yàn)對(duì)比了三種算法挖掘帶約束CARs消耗的時(shí)間,實(shí)驗(yàn)中minconf=50%,約束集β根據(jù)屬性值的選擇率s進(jìn)行模擬.例如:Pumsb數(shù)據(jù)庫(kù)擁有2113不同的屬性值,20%選擇率約為423個(gè)屬性值作為數(shù)據(jù)約束.由圖6測(cè)試結(jié)果可知,隨著minsup降低,本文提出算法LD-CAR性能優(yōu)于改進(jìn)的CCAR算法與類Apriori的MAC算法,尤其在隨著minsup不斷變小的過程中,LD-CAR算法時(shí)間消耗增加緩慢,尤其在Pumsb這類數(shù)據(jù)集龐大且稠密的數(shù)據(jù)集上性能優(yōu)勢(shì)更加明顯.經(jīng)試驗(yàn)分析可明顯看出,本文引入基于差集的擴(kuò)展概念格結(jié)構(gòu)后,通過存儲(chǔ)差集信息能夠快速計(jì)算子結(jié)點(diǎn)類別支持度,有效提高結(jié)點(diǎn)生成效率,關(guān)聯(lián)分類規(guī)則提取算法有效壓縮了搜索空間,從而加快了算法的收斂速度.
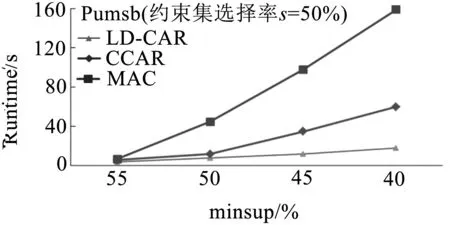
(a) Chess數(shù)據(jù)庫(kù)
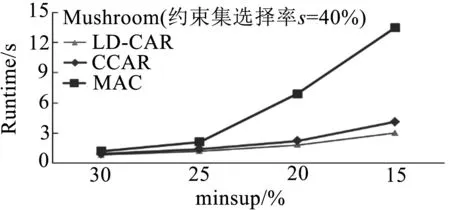
(b) Mushroom數(shù)據(jù)庫(kù)
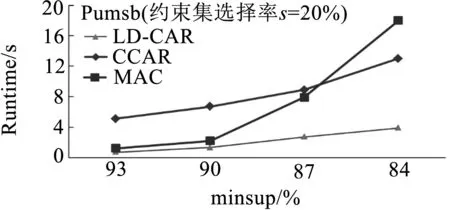
(c)Pumsb數(shù)據(jù)庫(kù)圖6 擴(kuò)展概念格二層結(jié)點(diǎn)與高層結(jié)點(diǎn)計(jì)算過程
5.2 內(nèi)存使用
實(shí)驗(yàn)對(duì)比了CCAR與本文算法LD-CAR的內(nèi)存使用情況,內(nèi)存占用主要取決于算法采用存儲(chǔ)結(jié)構(gòu),CCAR采用樹形結(jié)構(gòu),本文LD-CAR采用基于差集的擴(kuò)展概念格結(jié)構(gòu),對(duì)比結(jié)果如表3所示.可以看出在不同數(shù)據(jù)庫(kù)中LD-CAR算法均占用較少內(nèi)存,尤其在記錄數(shù)龐大的稠密數(shù)據(jù)庫(kù)Chess與Pumsb中,兩個(gè)項(xiàng)目集鏈接后的孩子結(jié)點(diǎn)僅存儲(chǔ)差集信息極大降低了格空間占用.

表3 兩種算法內(nèi)存使用對(duì)比
6 結(jié)論
本文在深入研究關(guān)聯(lián)分類理論的基礎(chǔ)上,提出了一種基于擴(kuò)展概念格的帶約束關(guān)聯(lián)分類挖掘方法. 該方法主要分為兩個(gè)步驟:擴(kuò)展概念格的建立和在其上的帶約束關(guān)聯(lián)規(guī)則提取. 算法設(shè)計(jì)基于差集的擴(kuò)展概念格結(jié)點(diǎn)結(jié)構(gòu),根據(jù)用戶需求引入約束條件控制挖掘方向,并給出了相應(yīng)格構(gòu)建算法和在其上的關(guān)聯(lián)分類規(guī)則提取算法;該方法優(yōu)勢(shì)如下:
(1)設(shè)計(jì)擴(kuò)展概念格結(jié)構(gòu),每個(gè)結(jié)點(diǎn)中包含全部的頻繁項(xiàng)集信息,該結(jié)構(gòu)在不丟失有效信息的前提下降低了建造整個(gè)格的復(fù)雜度,應(yīng)用定理可有效縮減了擴(kuò)展概念格中結(jié)點(diǎn)的數(shù)目,避免了由于候選項(xiàng)目集結(jié)點(diǎn)產(chǎn)生過多導(dǎo)致效率低下問題;
(2)在擴(kuò)展概念格高層結(jié)點(diǎn)結(jié)構(gòu)中引入差集概念,可加快結(jié)點(diǎn)鏈接操作運(yùn)算時(shí)間.高層格結(jié)點(diǎn)中存儲(chǔ)差集信息代替存儲(chǔ)記錄集也可有效減少內(nèi)存占用;
(3)該算法非常適合重用.當(dāng)約束條件集根據(jù)用戶需求發(fā)生改變時(shí),格無(wú)需重新建立,重新挖掘的時(shí)間大大減少了,滿足重用性要求.
進(jìn)一步的工作可以考慮將本文算法推廣到大數(shù)據(jù)環(huán)境中,研究分布式輔助關(guān)聯(lián)分類,還可以對(duì)分類器進(jìn)行動(dòng)態(tài)調(diào)整[12],使算法挖掘的結(jié)果更具參考價(jià)值.

