一類非線性四階偏微分方程的精確解研究

趙欣，李秀梅，汪穎 ，張繼紅，梁波

(大連交通大學 理學院，遼寧 大連 116028) *

非線性偏微分方程的精確解研究在實際中十分重要.研究方法上包括李群對稱分析方法、級數展開法等.文獻[1-2]利用Backlund變換并結合李對稱分析方法和冪級數展開法對一類非線性偏微分方程給出了精確解分析.文獻[3-4]則研究了一類非線性四階偏微分方程的精確解.文獻[5]對一類非線性四階偏微分方程求出數值結果.本文是結合經典方法，對四階非線性偏微分方程進行計算和研究得出求精確解的一種方法.

本文研究一類非線性四階偏微分方程：

(1)

的精確解，其中k,λ,μ,c,f,g,h均為常數.

1 精確解分析

1.1 方程處理

令u(x,t)=φ(x,t)+R,代入到式(1)中有

(2)

對式(2)進行約化有

(3)

令Φ=φ-φx，為了使式(3)中的每一項依賴于Φ或Φ的微分，要求其系數滿足條件：

解得

于是式(3)轉化為

(4)

1.2 求解過程

這里考慮兩種情況：

情況一：當λ≠0時,考慮方程Φ=0，即

φ-φx=0.

基本解組為φ(x,t)=A(t)ex

其中A(t)是任意函數.

情況二：當λ=0,k≠0時，則式(4)化為

-kΦxx-Φtt+kΦxxx=0

(5)

此時介紹三種研究方案：

方案一：若

Φ=φ-φx,φ-φx=cx+dt

其中c,d為任意常數.可求得基本解組為

φ(x,t)=A(t)ex+cx+dt

其中，A(t)是任意函數.

方案二：若

Φ=φ-φx，φ-φx=x2-kt2,

故基本解組為：

φ(x,t)=A(t)ex+x2-kt2,

其中A(t)是任意函數.

方案三：若Φ=φ-φx，

φ-φx=x3-3k(x-1)t2

基本解組為

φ(x,t)=A(t)ex+x3-3k(x-1)t2

其中A(t)是任意函數.

1.3 推廣

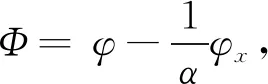
(6)

對式(6)求解得

故式(3)轉化為

(7)

此時考慮兩種情況.

情況一：λ≠0,考慮方程Φ=0.求得基礎解組為

φ(x,t)=A(t)eαx

其中A(t)是任意函數.

情況二：當λ=0,k≠0時，則式(7)轉化為

(8)

此時有如下方案給出精確解.

方案一：若

Φ=φ-φx，φ-φx=cx+dt+e

其中c,d,e為任意常數. 基本解組為

φ(x,t)=A(t)eαx+cx+dt+e

其中A(t)是任意函數.

方案二：若Φ=φ-φx,

其中b,e,c為任意常數. 基本解組為

其中A(t)是任意函數.

由方案一和方案二，可得廣義形式

這里假設函數f(x)和g(t)分別關于x和t足夠光滑，且f?(x)=0.若滿足條件

kfxx+αgtt=0.

此時基本解組為

φ(x,t)=A(t)eαx+f(x)+g(t)

其中A(t)是任意函數.

方案三：若Φ=φ-φx,

其中a,b,c為任意常數.

它的基本解組為

其中A(t)是任意函數.

方案四：若Φ=φ-φx,

其中a,b,c為任意常數.

它的基本解組為

其中A(t)是任意函數.

由方案三和方案四，可得廣義形式：

這里假設函數g(t),f(x)及h(x)足夠光滑.

若g″(t)=0，及

或者，若g″(t)=c(c≠0)，只要滿足下面條件

基本解組為

φ(x,t)=A(t)eαx+f(x)+h(x)g(t)

其中A(t)是任意函數.

2 一類三階方程的算法擴展

考慮三階非線性偏微分方程，形式如下

(9)

其中f關于x至少具有一階導數，μ,a,b,c,k,r,w均為常數.

令u(x,t)=φ(x,t)+R，將其代入式(9)得：

(10)

將式(10)進行約化得：

(11)

令Φ=φxx+αφx+βφ+f，其中β≠0,α為任意常數. 為使式(11)的每一項均包含Φ或者Φ的n階導數，則系數須滿足關系

故將(11)化為

-βΦt+βφxΦ+βφΦx=kΦ

(12)

此時只需求解方程Φ=0，同時注意到Φ=φxx+αφx+βφ+f=0是二階常系數非齊次線性微分方程，易得該方程一般形式的解. 為獲得式(9)一系列精確解，可進行變形，式(11)的每一項都依賴于Φ或者Φ的n階微分，那么當φ(x,t)是方程Φ=0的解時，則φ(x,t)是式(12)的解. 實際上，在式(12)中，當φ(x,t)是方程Φ=0的解時，φ(x,t)也是(9)的解. 通過改變常數的值，推廣了方程Φ=0的基礎解，從而得到了(9)一系列精確解.

3 精確解波形圖分析

根據所求得的精確解，繪圖時都取λ=1,k=-4,α=1；利用Matlab軟件將幾個典型的波形圖繪制如圖1～4所示.

(1)A(t)=sin(t)+cos(t),x∈[-20,20],t∈[-10,10]時，其波形如圖1所示.

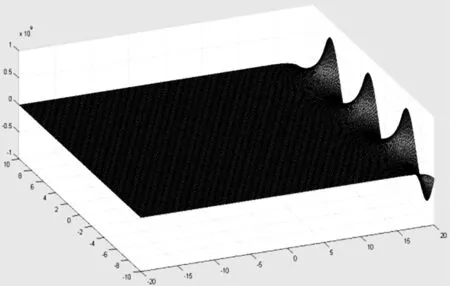
圖1 x∈[-20,20],t∈[-10,10]時波形圖

(2)A(t)=sin(t)+cos(t),x=-2,t∈[-10,10]時， 其波形如圖2所示.

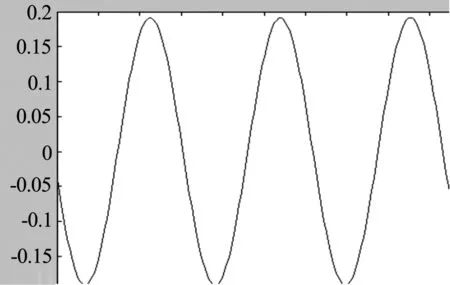
圖2 x=-2,t∈[-10,10] 時波形圖

(3)A(t)=sh(t),x∈[-1,1],t∈[-50,50]時，其波形如圖3所示.

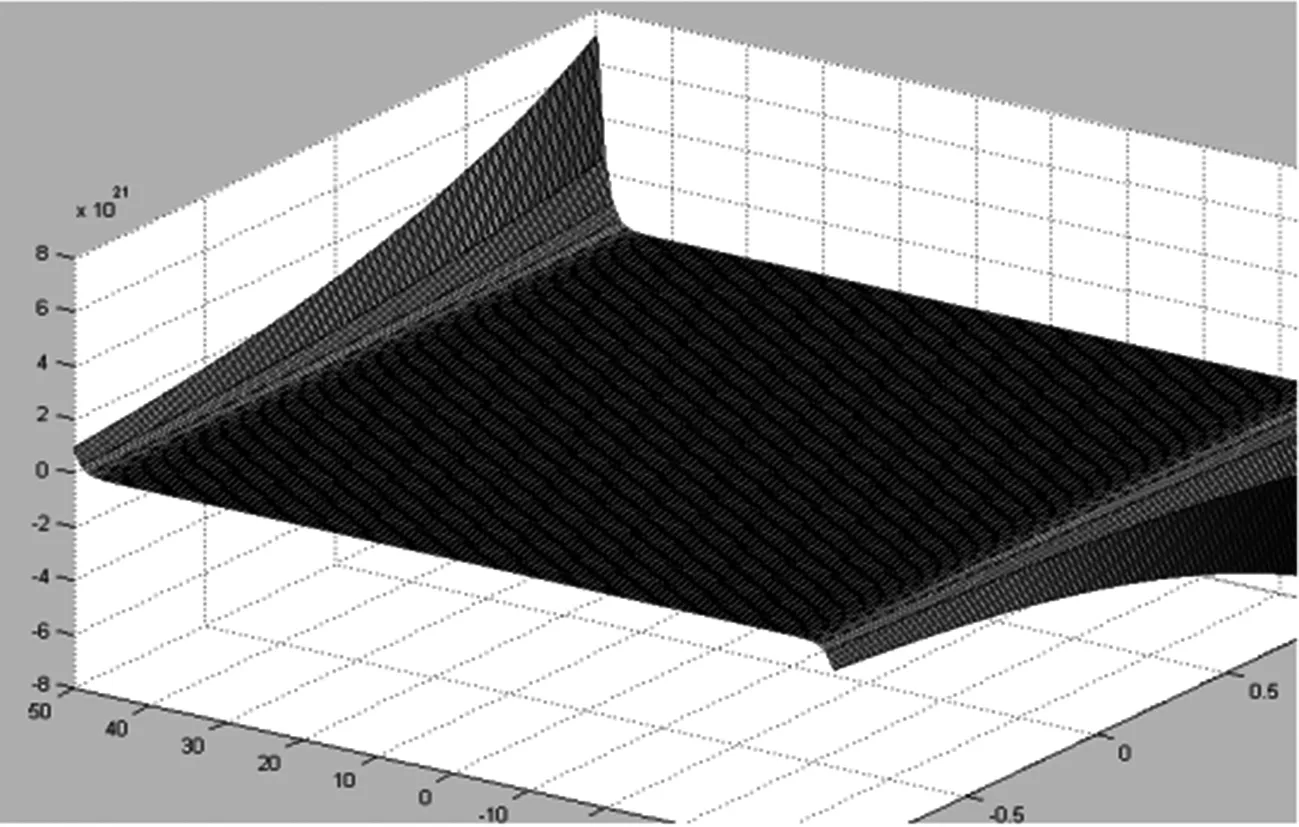
圖3 x∈[-1,1],t∈[-50,50]時波形圖

(4)A(t)=sh(t),x=-1,t∈[-50,50]時，其波形如圖4所示.

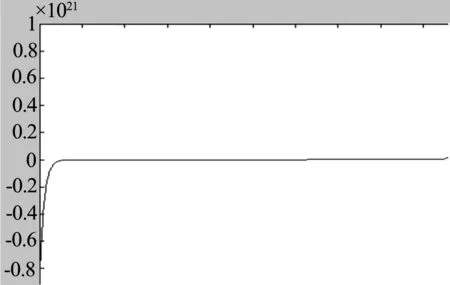
圖4 x∈[-1,1],t=50時波形圖

4 結論

本文通過將非線性四階偏微分方程約化為常微分方程的方法，簡化了方程結構及復雜的計算，從而獲得解的基本形式. 利用參數的變化取得一系列精確解. 遵循四階方程研究的研究思路，將精確解求法推廣到一類三階非線性偏微分方程上. 最后， 利用Matlab軟件繪制出了幾個典型情形下

的波形圖. 本文的方法為簡化求解提供了參考.