高速再入飛行器分數階PIλDμ穩定域分析

秦昌茂 王 興 雷延花

中國運載火箭技術研究院，北京 100076

0 引言

高速飛行器再入過程中，由于馬赫數高達10以上，飛行中氣動參數受到馬赫數及攻角變化的影響，導致高速飛行器是一類參數大范圍快速時變、強非線性的復雜被控對象，傳統PID控制往往難以獲得滿意的控制效果，而目前普遍應用的魯棒控制、自適應控制及滑模控制等[1-5]，雖然控制效果很好，但是增加了控制器設計的復雜程度，并且也沒有對高速飛行器的穩定域進行相應的分析。

分數階PIλDμ[6]將傳統PID的整數階次推廣到分數階次，由于比傳統PID具有更強的魯棒性及更好的控制效果[7-8]及繼承了傳統PID結構簡單等特點，分數階PIλDμ在其他領域已獲得應用。分數階PIλDμ控制器設計過程包括數字實現及參數整定2部分，目前數字實現方法[9-10]中以薛定宇的改進Oustaloup算法獲得較好的近似效果。分數階PIλDμ相較于傳統PID增加了2個階次參數，目前的參數整定主要是通過優化算法來確定，有極點配置法、頻率法及遺傳算法[11]。在分數階PIλDμ的穩定域分析中，主要是使用D-分解法針對分數階系統[12-13]或是參數不確定時滯系統[14]分析控制器參數穩定區域，但并未整定λ和μ兩個參數。

本文基于最優Oustaloup數字實現及高速飛行器非線性俯仰通道模型建立仿真框圖，結合ITAE指標利用遺傳算法尋優整定分數階PIλDμ參數，然后針對選定的分數階PIλDμ控制器，利用D-分解法分析高速飛行器的馬赫數及攻角穩定區域，以確定所設計的控制器穩定控制范圍和控制參數，同時保證控制器具備最優的穩定性。最后結合跟蹤微分器設計了改進的分數階PIλDμ控制器。

1 分數階PIλDμ最優Oustaloup數字實現

基于Oustaloup濾波器在(ωb,ωh)頻率段內實現分數階微分算子sμ的近似，在該濾波器之前增加一個濾波器來提高數字實現近似精度，將分數階微積分sμ近似為：

sμ≈G×Gc

(1)

其中G為濾波器，Gc為Oustaloup濾波器。

濾波器G的形式為：

(2)

其中的參數通過最優算法尋優確定。為了提高頻率段內幅頻及相頻近似精度，將分數階微積分sα近似算法的幅頻及相頻與實際的幅頻及相頻之間的誤差作為尋優性能指標，即：

(3)

其中，M1和P1代表實際的幅頻及相頻，M2和P2代表近似算法的幅頻及相頻，ρ為調整因子，可以調整幅頻及相頻近似的側重。一般取ρ=0.5。通過尋優使得J達到最小來確定濾波器G的參數。

以分數階算子s0.5為例，取頻率段為[0.001，1000]，N=4，以改進算法中的濾波器參數作為優化的初始值，經過尋優之后，得到最優參數為：

分別利用Oustaloup算法及最優Oustaloup算法進行仿真，頻率響應曲線如圖1所示。

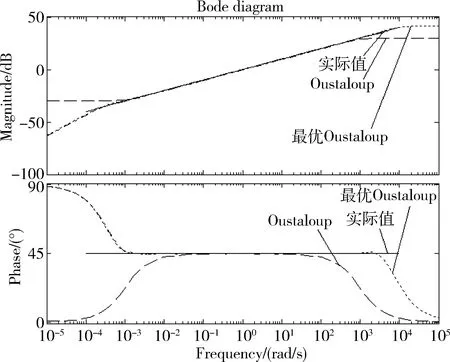
圖1 分數階算子s0.5頻率響應曲線

分數階PIλDμ微積分階次一般取λ,μ∈[0 ∶0.1 ∶1]，最終設計的分數階PIλDμ框圖如圖2所示。

圖2 分數階PIλDμ仿真圖

2 分數階PIλDμ參數整定

以高速飛行器俯仰通道為例，俯仰通道模型如下：

(4)

其中：

r=h+RE

CL=0.6203α

CM(α)=-0.035α2+0.036617α+5.3261×10-6

CM(δe)=ce(δe-α)

式中：V，θ，h，α和ωz分別表示飛行器的速度，彈道傾角，高度，攻角和俯仰角速度；L，Mz分別表示升力和俯仰力矩；m，Iz，μ，S和RE分別表示飛行器的質量、俯仰轉動慣量、重力常數、參考氣動面積和地球半徑。其中飛行器仿真模型的參數見參考文獻[1]。

遺傳算法是一類借鑒生物界自然選擇和生物遺傳機制的隨機化搜索方法，其主要特點是群體搜索策略和群體中個體之間的信息交換，優化搜索不依賴于梯度信息，尤其適合于處理傳統搜索難以解決的復雜性和非線性問題。建立分數階PIλDμ控制器及高速飛行器俯仰通道非線性模型，結合ITAE指標，利用遺傳算法尋優整定分數階PIλDμ參數，積分及微分階次取μ,λ∈[0 ∶0.1 ∶1]，參數Kp,Ki,Kd∈[1,100]，高度h=30km，V=15，期望值α=10°，仿真結果如圖3所示。

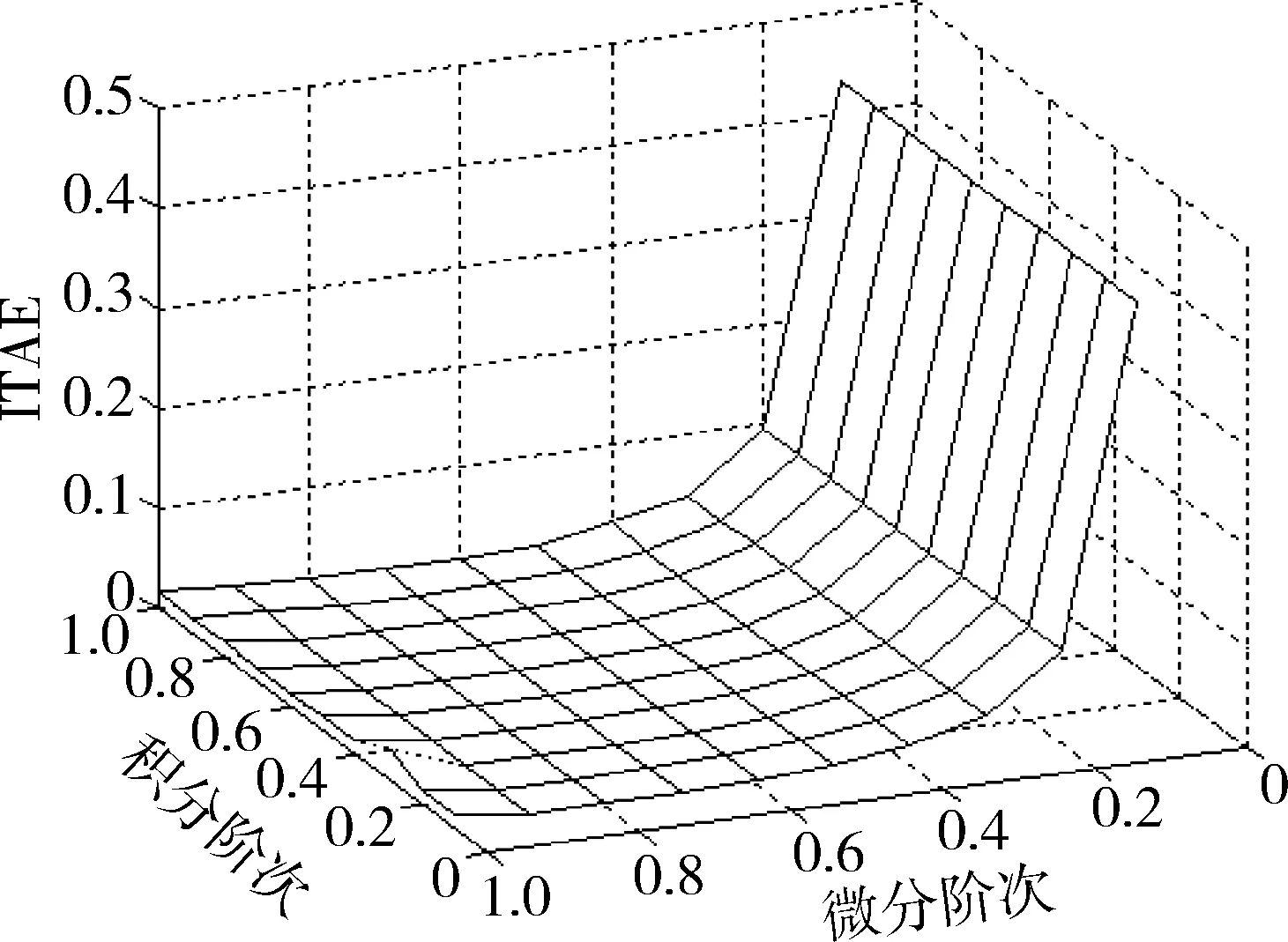
圖3 不同λ和μ的ITAE值

從仿真結果可以看出，分數階PIλDμ比傳統PID可以獲得更好的控制品質。

3 馬赫數及攻角穩定域分析

將高速飛行器俯仰通道模型轉化為非線性傳遞函數，被控系統模型為馬赫數及攻角的函數。

(5)

其中：

A=s2+0.04078Vα2s-

0.001809Vαs+0.0013734Vs

B=-0.0015785V2α2+

0.0003344V2α+2.402×10-7V2

D=0.001317V2

選擇分數階PIλDμ控制器模型為：

C=Kp+Kis-λ+Kdsμ

因此，系統閉環傳遞函數為：

(6)

特征多項式為：

P(s;V,α)=
sλ(Aα+AC-B)+Dα·(Kdsλ+μ+Kpsλ+Ki)

(7)

定義1：設馬赫數和攻角的穩定域為S，當K=(V,α)∈S時，控制系統穩定的條件是特征根均在s平面的左半部。

穩定域S由實部邊界(Real region boundary，RRB)，虛部邊界(Imaginary region boundary，IRB)及復數邊界(Complex region boundary，CRB)確定，3條邊界線由D-分解法計算確定。邊界由以下方程確定：

RRB：P(0;K)=0；IRB：P(∞;K)=0；

CRB：P(±jω;K)=0

將s=0代入到特征多項式中可得RRB邊界線方程為：V=0。

由于高速飛行器俯仰通道傳遞函數分子分母最高階次不相等，因此沒有IRB邊界線。

將s=jω代入特征多項式，可得CRB邊界線方程。

復數的分數次方計算公式為：

其中，σ為實部，ω為虛部，γ為階次。

利用上式可得：

將上式令特征多項式代入特征多項式，令實部及虛部都等于0，可得關于V與α的方程，其中ω∈(0,∞)，所得數值解中取V>0，則穩定域邊界為RRB在α=∞時與CRB相接，穩定區域為CRB邊界曲線上方。

以分數階PIλDμ控制器：

C=100(1+s-0.5+s0.9)

(8)

為例得到的方程如下所示：

0.06585V3α+0.014566V3αω1.4+
0.0011164V3α2ω0.5+0.092889V3αω0.5-
0.7071Vαω2.5+4.1393×10-5Vαω0.5-
0.000031426Vω0.5-1.2438×10-7V3ω0.5+
2.5087×10-5V3α3ω0.5-9.3312×10-4Vα2ω0.5=0
0.028836V2α3ω1.5+0.091979V3αω1.4+
0.0000331V2ω1.5-0.022882ω1.5-0.06585V3α-
0.0012791V2α2ω1.5+0.0015863V2αω1.5=0

(9)

解上述方程，即可得到V與α的穩定域邊界。

3.1 λ對穩定域的影響

取μ=1，λ分別為0、0.2、0.4、0.6、0.8和1，得到高速飛行器V與α的穩定域如圖4所示。

圖4 λ變化時對穩定域的影響

從圖中可知，隨著λ的增大，穩定域不斷減小，在攻角α∈[5°,15°]內變化很明顯。傳統PID的穩定域最小，而分數階PIλDμ擴大了穩定域，說明分數階PIλDμ比傳統PID對系統參數的變化不敏感，且應用的范圍更廣，所以λ應取分數階次并取較小值。

3.2 μ對穩定域的影響

取λ=1，μ分別為0.2、0.4、0.6、0.8、1，得到高速飛行器V與α的穩定域如圖5所示。

圖5 μ變化時對穩定域的影響

從圖中可知，隨著μ的增大，穩定域先減小后增大，μ取較小值時，穩定域范圍比傳統PID小，當μ取0.6～0.8時，穩定域基本不變，比傳統PID穩定域范圍大，所以μ應取較大值。

4 改進的分數階PIλDμ控制器

跟蹤微分器(Tracking differentiator，TD)是自抗擾控制技術的重要組成部分，主要是解決在工程實際問題中，有效的給出不連續或有噪聲的信號的跟蹤信號和信號的微分。即跟蹤微分器給出輸入信號的跟蹤信號以及跟蹤信號的微分，用跟蹤信號的微分來近似輸入信號的微分。對于離散系統，具體算法如下[15]：

(10)

構造最速控制綜合函數fhan(x1,x2,r,h)，算法如下：

(11)

將u=fhan(x1,x2,r,h)帶入系統中，以x1(k)-v(k)代替方程中的x1(k)，就可以得到離散化的跟蹤微分器：

(12)

其中，v(k)為輸入信號，x1(k)為輸入信號的跟蹤信號，x2(k)為x1(k)的微分信號，可近似看為v(k)的微分信號，r為快速因子，r越大x1(k)跟蹤v(k)也越快。h為濾波因子。

利用跟蹤微分器改進分數階PIλDμ控制器，將兩者結合，為便于設計控制器，并結合前文的性能指標分析及分數階次對穩定域的影響分析，選擇分數階次λ=0.2，μ=1。在穩定域滿足實際應用的前提下，μ=1可以直接利用跟蹤微分器輸出的微分信號，如果μ≠1，可以直接加入分數階PIλDμ微分對信號進行分數階微分計算。

建立高速飛行器縱向通道非線性模型，構造如圖6所示的高速飛行器俯仰通道自抗擾分數階PIλDμ控制器：

圖6 高速飛行器縱向通道控制框圖

仿真參數選取如下：r0=300，h0=0.1，r1=300，T=0.001，其中，r0,h0分別為前向通路的快速因子和濾波因子，r1,h1為反饋通路的快速因子和濾波因子和T為采樣時間，當V=15，期望輸入α=10°，在輸入信號中加入高斯白噪聲及第5s時加入幅值10°的脈沖信號，仿真結果如圖7所示。

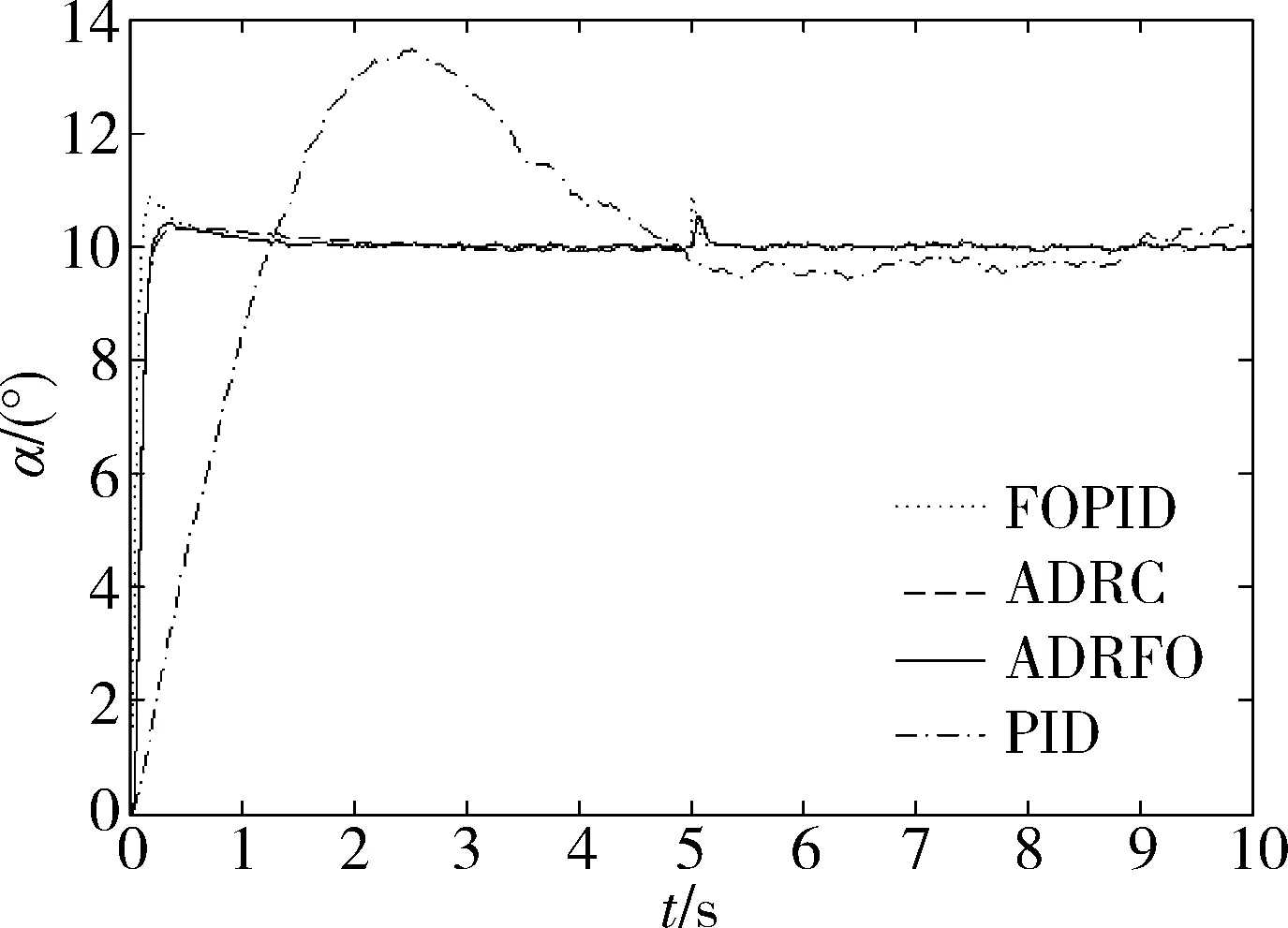
圖7 控制器仿真結果

從圖中可以看出，分數階PIλDμ控制器上升時間短，響應快，能更好的滿足高速飛行器的快速性要求，具有更高的穩定精度，能精確地跟蹤控制指令達到期望值。而傳統PIλDμ上升時間長，響應速度慢。

分數階PIλDμ(FOPID)、自抗擾(Active disturbance rejection controller，ADRC)及自抗擾分數階PIλDμ(Active disturbance rejection and Fractional-order PID，ADRFO)均比傳統PID控制效果好，調節時間及超調量均優于傳統PID，獲得了更好的控制品質。而分數階PIλDμ相比于自抗擾及自抗擾分數階PIλDμ調節時間減少，但是超調量稍大，自抗擾超調最小，但是調節時間稍大，自抗擾分數階PIλDμ介于兩者之間。

從圖7可知，當α=10°，V=2.7時，對于傳統PID及自抗擾控制器而言，該系統是不穩定的。但是對于分數階PIλDμ而言，該系統是穩定的，仿真結果如圖8所示。

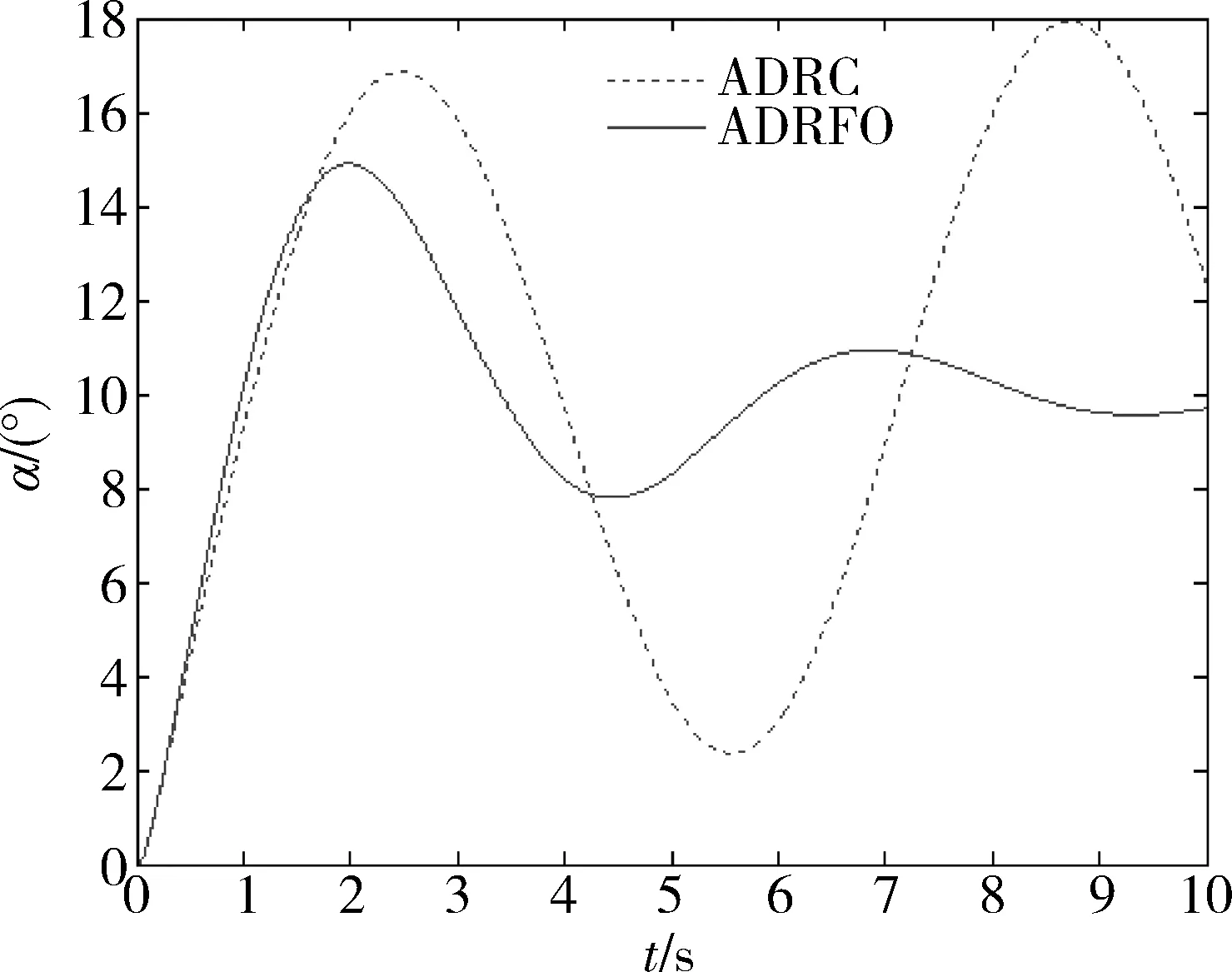
圖8 控制系統穩定性分析

自抗擾控制仿真結果是發散、不穩定的，而自抗擾分數階PIλDμ仿真結果是收斂、穩定的。由此，可以看出，自抗擾控制雖然設定了過渡過程時間，并且在超調量及調節時間方面有了很大改進，但是穩定域還是繼承了傳統PID的特點。而分數階PIλDμ則擴展了傳統PID的穩定域，提高了控制器的魯棒性。因此結合自抗擾控制器及分數階PIλDμ控制器的優點，在提高控制品質的同時，提高了被控系統的穩定域，也提高了控制器的魯棒性。

5 結論

利用最優Oustaloup數字實現算法及遺傳算法設計了高速飛行器的分數階PIλDμ姿態控制器，并結合D-分解法計算出在確定的分數階PIλDμ控制器下馬赫數及攻角的穩定域。自抗擾分數階PIλDμ通過跟蹤微分器改進分數階PIλDμ控制器，結合了自抗擾技術及分數階PID控制器的優點，在噪聲和大幅干擾存在的情況下，控制器仍然有較好的控制品質，且在解決快速性及超調量之間矛盾的同時，獲得了較大的穩定域。仿真結果證明分數階PIλDμ繼承了傳統PID結構簡單等優點，獲得更好的控制品質和更強的魯棒性，滿足高速飛行器快速性的要求，在馬赫數及攻角大范圍內變化的情況下也能保證控制品質及控制系統穩定。對于設計高速飛行器全程姿態控制系統，具有工程應用價值。