一種諧振倍壓電路型串聯超級電容電壓均衡器
楊曉光,劉介桃,齊亞康,陳玫琪
(1.河北工業大學省部共建電工裝備可靠性與智能化國家重點實驗室,天津 300130;2.河北工業大學河北省電磁場與電器可靠性重點實驗室,天津 300130)
超級電容作為一種新興的儲能器件,在儲能系統中得到了廣泛應用。由于超級電容單體額定電壓較低,為了滿足電壓和儲能容量的需求,需要將多個超級電容單體串聯使用[1]。然而,由于單體超級電容在容量、內阻和自放電率等方面存在差異,實際應用中會造成單體超級電容之間的電壓逐漸趨于不平衡。電壓不平衡問題會引起某些超級電容的過充和過放現象[2],使得系統容量不能得到充分利用,影響超級電容使用壽命,甚至造成火災、爆炸等危險事故。
目前已經提出了多種電壓均衡技術來解決電壓不平衡的問題,相比于被動型均衡電路,主動型均衡電路的均衡速度快,均衡效率高,是一種更具有發展前景的解決方法。傳統主動均衡技術主要采用雙向DC/DC 變換器,電感或電容以及變壓器作為能量交換的均衡方案。基于雙向DC/DC 變換器的電壓均衡器[3-4]需要大量的可控開關,也就需要對應數量的驅動電路,系統復雜性較大。基于變壓器的均衡方案[5-6]具有較少的變換器和可以自動直接對單元均衡的優點,但二次繞組間參數匹配要求嚴格,給設計帶來困難,擴展性降低。文獻[7-8]采用開關電容用于單元間均衡,這類均衡器具有良好的擴展性,但所需均衡器的數量與串聯的單元數量成正比,增加了系統的復雜度和成本。由于多倍壓電路僅由二極管和電容組成,因此基于多倍壓電路的均衡器電路簡單,可擴展性好。典型的多倍壓電路為Cockcroft-Walton(CW)電路[9-10],如圖1(a)所示。另外一種改進型倍壓均衡電路如圖1(b)所示,此類均衡電路存在均衡電流疊加現象,因而電流紋波較大,并且均衡速度較慢,均衡器中的開關管采用硬開關方式[11-12]。
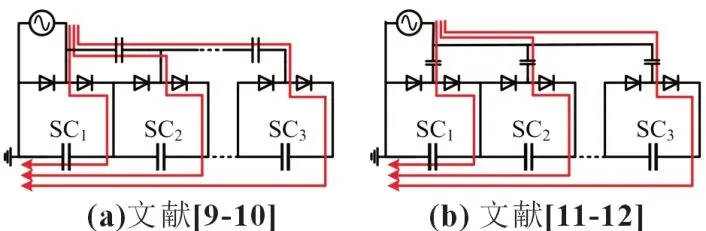
圖1 基于多倍壓電路的均衡器
針對上述問題,本文提出了一種基于諧振倍壓電路的電壓均衡器,此均衡器主要由半橋諧振變換器和對稱式倍壓電路組成。半橋諧振變換器驅動控制簡單并且實現了軟開關;對稱式倍壓電路均衡速度快,無電流疊加問題,二極管實現了軟開關,無反向恢復問題。
1 均衡器的結構
本文所提出的均衡器拓撲如圖2 所示,主要由半橋諧振變換器和對稱式倍壓電路組成。QH和QL組成半橋,Lr為諧振電感,Cr為諧振電容,T 為變壓器,Lr和Cr在QL兩端的方波電壓的驅動下進行諧振。變壓器的副邊接對稱式倍壓電路,C1a-Cna和C1b-Cnb為耦合電容,D1a-D1d…Dna-Dnd為二極管,SC1-SCn為儲能系統的串聯超級電容。串聯超級電容SC1-SCn經半橋諧振變換器與對稱式倍壓電路優先將能量傳遞給SC1-SCn中電壓最低的超級電容,從而實現將SC1-SCn的電壓VSC1-VSCn均衡一致。
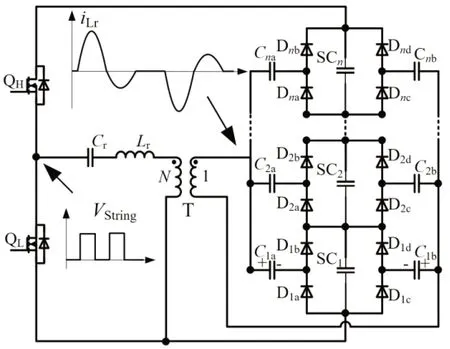
圖2 基于半橋諧振變換器和對稱式倍壓電路的電壓均衡器
2 穩態分析
2.1 工作原理
由于超級電容容量大,并且均衡器工作頻率高,因而在一個開關周期內將超級電容等效成一個恒壓源,假定對稱式倍壓電路中所有的二極管以及耦合電容完全一致。圖3 給出了當SC1電壓最低時,兩種開關狀態分別對應的工作模態圖。電路的關鍵波形如圖4 所示,D為占空比,ts為開關周期。[t0~t3]時段,開關管QH導通,[t3~t6]時段,開關管QH關斷,QL與QH互補導通。
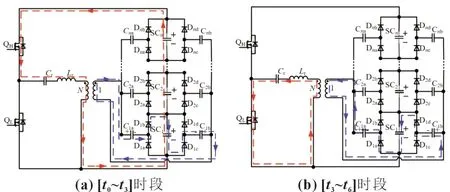
圖3 當SC1電壓最低時對應的工作模態圖
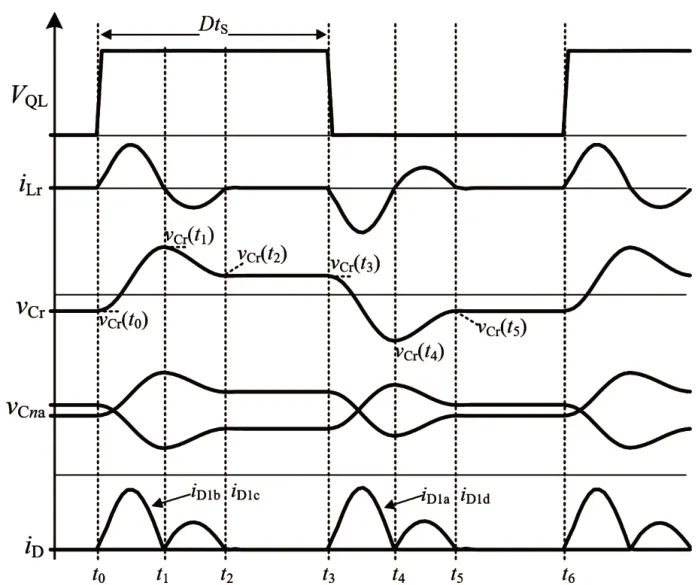
圖4 關鍵波形圖
[t0~t3]時段:QH導通,QL關斷,串聯的超級電容與Lr和Cr諧振腔以及變壓器原邊組成諧振回路,諧振電流經變壓器傳遞至副邊,變壓器副邊、耦合電容、二極管與電壓最低的儲能超級電容形成回路。[t0~t2]時段諧振電流不為零,變壓器給后級傳能。[t2~t3]時段諧振電流為零,Cr兩端電壓維持不變,變壓器不傳遞能量。
在t0時刻,QH導通,串聯的Lr和Cr兩端承受高壓,諧振開始,流過QH的電流從零值開始上升,電流上升速度受到Lr和Cr諧振腔限制,QH實現零電流開通。在t3時刻,QH關斷時,諧振電流已經截止,流過QH的電流為零,因此QH為軟關斷。
[t3~t6]時段:QH關斷,QL導通,Lr和Cr諧振腔以及變壓器原邊組成諧振回路,諧振電流經變壓器映射至副邊,變壓器副邊、耦合電容、二極管與電壓最低的儲能超級電容形成回路。這個時段是Lr和Cr諧振腔釋放能量,[t3~t5]時段諧振電流不為零,變壓器給后級傳能。[t5~t6]時段諧振電流值為零,Cr兩端電壓維持不變,變壓器不傳遞能量。
在t3時刻,QL導通,Cr兩端電壓不再維持不變,Cr中的能量開始釋放,流過QL的電流從零值開始上升,電流上升速度受到Lr和Cr諧振腔限制,QL實現零電流開通。在t6時刻,QH關斷時,諧振電流已經截止,流過QL的電流為零,因此QH為軟關斷。
由以上分析可知:所提出的均衡器工作諧振電流斷續模式(如圖4 中iLr所示)兩個可控開關管都可以實現軟開關,并且如圖4 中iD所示,流過二極管的電流自然諧振到零,實現二極管軟關斷。
2.2 數學模型
為了簡化均衡器的描述,引入諧振電路特性阻抗Z0、特征角頻率ω0和諧振角頻率ωr,定義如下:
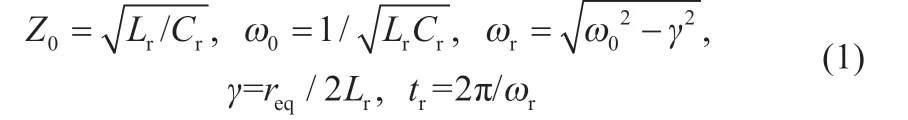
式中:req為諧振回路的等效電阻,等于變壓器一次側電阻與從變壓器二次側映射到一次側的等效電阻之和;tr為與ωr對應的諧振周期。
由于均衡電流和線路電阻都較小,則變壓器原邊電壓Vp表示為:
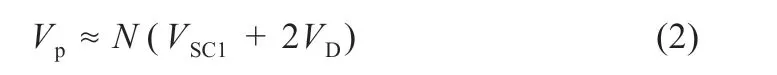
式中:Vp為從變壓器二次側映射到一次側的電壓;N是變壓器變比;VD為二極管壓降。
根據圖3 中的諧振回路可以列寫狀態方程如下:
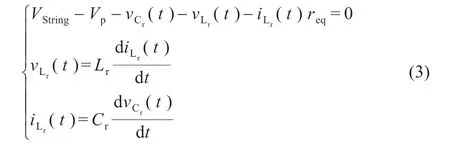
整個開關周期ts分為6 個工作模態,變換器主要工作波形如圖4 所示,各個模態分析如下:
模態1 [t0≤t≤t1]:t0時刻開始,電流iLr開始增加,通過變壓器映射到二次側,并流過電壓最低的超級電容SC1,諧振電流表達式和諧振電容電壓在t1時刻值分別表示為:
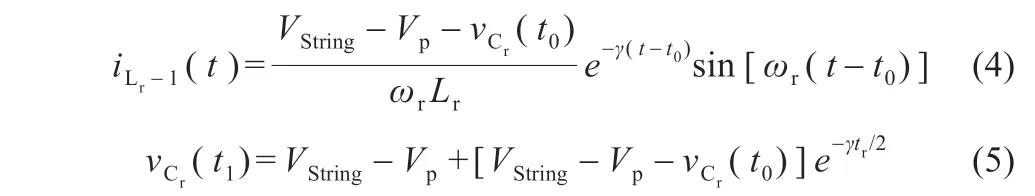
模態2 [t1≤t≤t2]:t1時刻后iLr反相,變壓器一次電壓Vp極性反向。在此模態,諧振電流表達式和諧振電容電壓在t2時刻值分別表示為:
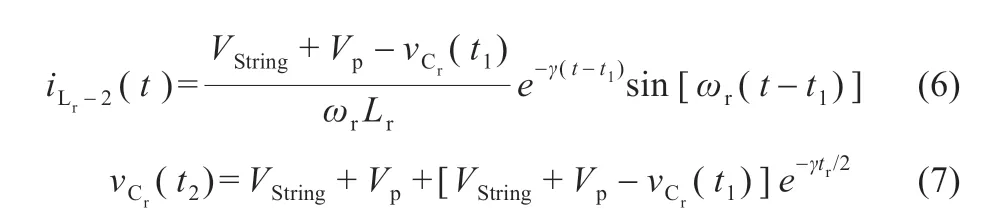
模態3 [t2≤t≤t3]:在t2時刻,iLr達到零值,并在此模態保持為零,且諧振電容的電壓維持不變:

模態4 [t3≤t≤t4]:t3時刻QH關斷,QL導通,此刻開始諧振電容電壓不再維持不變,開始釋放能量進行諧振,同理可以得出此模態諧振電感電流表達式和諧振電容電壓在t4時刻值表達式,分別為:
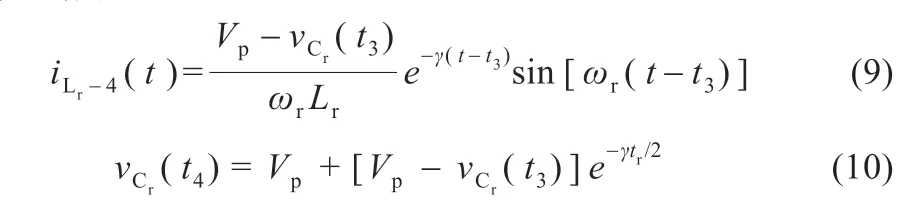
模態5 [t4≤t≤t5]:t4時刻,諧振電流換向,在此模態諧振電流表達式和諧振電容電壓在t5時刻值表達式分別為:
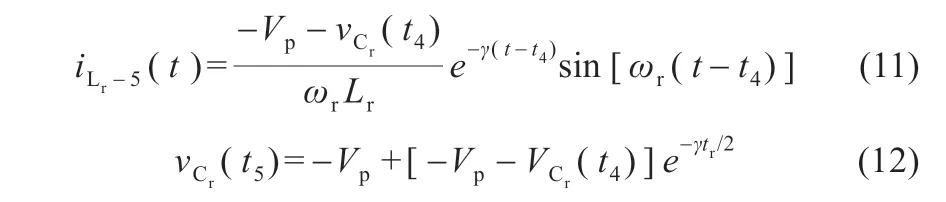
模態6 [t5≤t≤t6]:在t5時刻,iLr達到零,并在此模態保持為零,并且諧振電容的電壓保持恒定,直到下一個周期開始,可得:
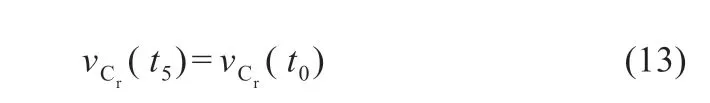
聯立式(5),(7),(8),(10),(12)和(13)可解得諧振電容電壓的各個時刻值如下:
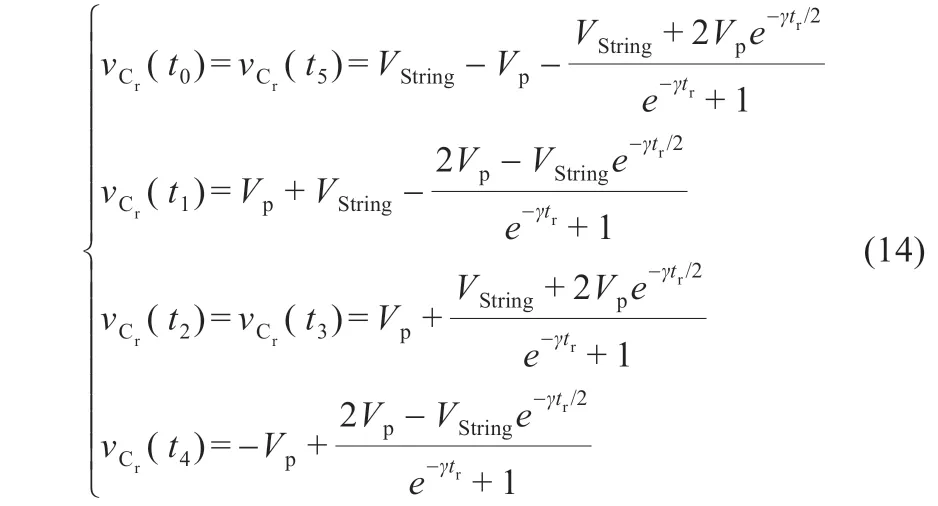
將式(14)分別代入式(4),(6),(9)和(11)可得到各個階段的諧振電流的表達式:
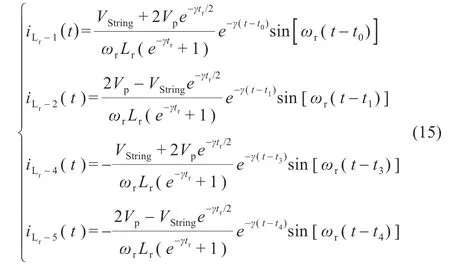
由式(15),將各個階段的諧振電流絕對值積分求和,并在一個開關周期ts時長內取平均,可得均衡電流平均值為:
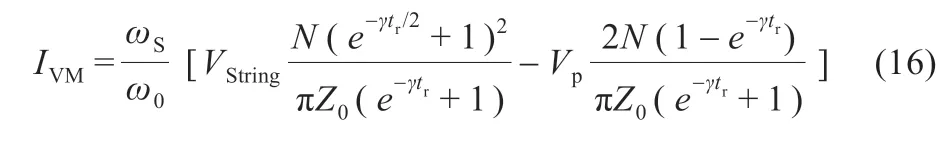
當電路各個器件選定以后,γ,ω0和tr不變,VString和Vp在短時間內不會有明顯變化,req很小可以忽略時,此時可以認為γtr趨近于零,因而式(16)可化簡為:

式中:fSN為開關頻率與諧振頻率的比值,其計算式為:

由式(17)可知,均衡電流IVM與fSN成正比關系,因此fSN可作為均衡電流的控制量,可以根據需要調節開關頻率達到調節均衡電流大小的目的。
2.3 運行條件
本文中,均衡器設計運行于iLr斷續工作模式,此模式下均壓器開關損耗小,還具有均衡電流控制簡單的優點。工作在斷續模式需要模態2 存在反向諧振電流且模態3 不存在諧振電流。
若模態2 存在反向諧振電流,則根據式(15)可知:

若模態3 不存在諧振電流,則:
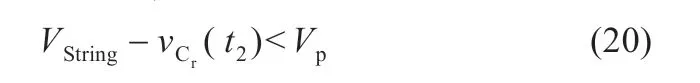
結合式(14),由式(20)可得:
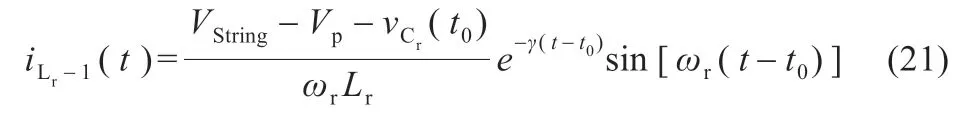
根據式(19)和(21),可得均衡器工作在斷續模式的條件為:
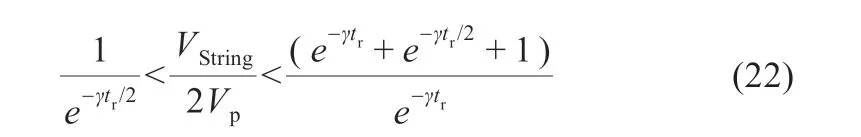
由于req很小,可以忽略,式(22)可化簡為:

因而,VString與Vp需要滿足式(23)的條件限制,均衡器才能工作在斷續工作模式。
3 均衡器參數設計
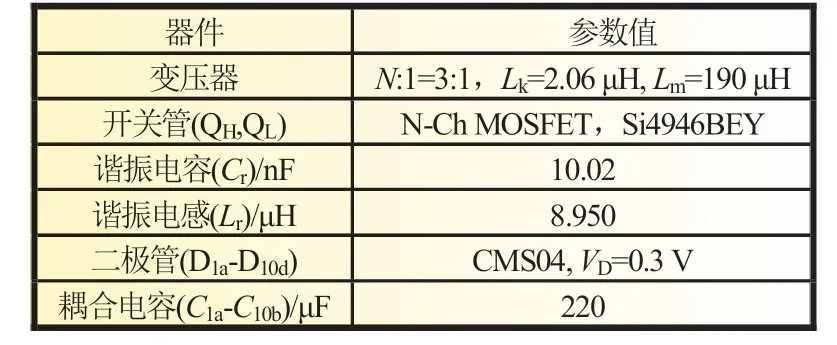
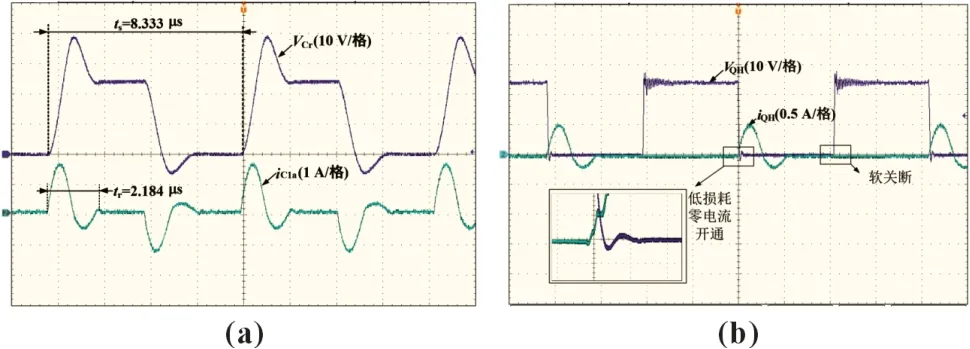
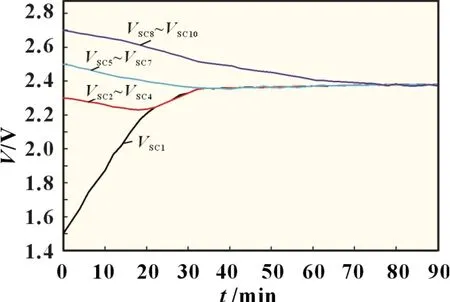
均衡器設計的第一步是選擇變壓器變比N:當串聯超級電容總電壓VString和單個超級電容電壓VSC范圍確定后,由式(2)和(23)可確定變壓器變比的取值范圍。本文中,VString=24 V,1.5 V Lr和Cr的選擇:首先,當開關頻率fS選定后,由于fSN<1/2,可選出諧振頻率f0。根據均衡電流IVM和N的取值,由式(17)可得到Z0。最后將得到的f0和Z0代入式(24)求得Lr和Cr。 本文選擇fS=120 kHz,fSN=1/4,f0=480 kHz,IVM=0.35 A,Z0=32.74 Ω,進而求得Lr=10.85 μH 和Cr=10.13 nF。 為了驗證分析結果和均衡器的特性,制作了樣機并進行了測試。表1 給出了實驗樣機參數。需要說明的是,為了便于檢驗均衡效果以及均衡速度,超級電容初始壓差設置較大并且均衡電流設置較大。 表1 樣機參數 圖5 給出了均衡器關鍵波形的實驗結果。圖5(a)所示的實驗波形與文中工作原理分析吻合(參見圖4),波形中的參數與理論模型計算結果一致。從圖5(b)可以看出,由于電流值從零開始諧振上升,開關管兩端電壓和開關管的電流交疊時間非常短,QH開通損耗非常小,基本上實現了軟開關;開關管QH為完全軟關斷。 圖5 關鍵波形實驗結果 采用10 個額定電壓2.7 V 的500 F 超級電容串聯作為儲能部分,各個超級電容的初始電壓分別為VSC1=1.5 V,VSC2=VSC3=VSC4=2.3 V,VSC5=VSC6=VSC7=2.5 V,VSC8=VSC9=VSC10=2.7 V,均衡電流設定為0.35 A,開關頻率fS=20 kHz,諧振頻率f0=480 kHz。均衡過程如圖6 所示:電壓最低的超級電容優先充電,電壓上升,最終各個超級電容電壓趨于均衡一致。初始各個超級電容電壓的標準差為356 mV,實驗結束時各個超級電容的電壓的標準差小于10 mV。 圖6 均衡測試中超級電容電壓變化曲線 本文提出的電壓均衡器具有可控開關少,控制簡單,擴展性強以及易于實現等優點。采用半橋諧振電流斷續工作模式保證了所有MOSFET 和二極管都能實現軟開關,并且在開環配置的情況下能夠控制均衡電流的大小。實驗結果驗證了數學模型的正確性。所提出的均衡器具有很好的均衡效果:對10 個串聯超級電容進行了均衡實驗,初始各個超級電容電壓的標準差為356 mV,實驗結束時各個超級電容的電壓的標準差小于10 mV。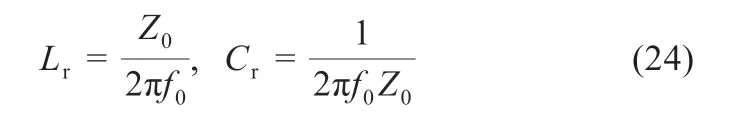
4 實驗驗證
5 結論

