基于機器學習的單站對流層延遲預測建模*
聶帥 葛雅倩 譚福臨 鐘東升
(安徽理工大學,安徽淮南 232001)
0.引言
誤差修正是GNSS測量及應用的關鍵環(huán)節(jié),雖然GNSS量測誤差的誤差來源較為復雜,但不同的衛(wèi)星系統(tǒng)的來源基本一致。與信號傳播有關的誤差對距離測量的影響為1.5m~15m。本文研究對流層延遲模型,屬于與信號傳播有關的誤差。在研究方法方面,本文使用機器學習算法中的偏最小二乘PLS與極限學習機ELM來建立數(shù)學模型,并將輸出結(jié)果與傳統(tǒng)的BP神經(jīng)網(wǎng)絡相對比。
陳陽等[1]利用BP神經(jīng)網(wǎng)絡誤差補償技術(shù),結(jié)合Hopif eld模型建立了適于北半球的融合模型。呂慧珠等[2]對ZTD的頻譜結(jié)構(gòu)進行研究,構(gòu)造預測模型,使用自回歸(AR)方法校正殘差,預測精度達厘米級。李偉捷等[3]為提高無氣象情況下ZTD預測的精準性,采用小波——AR組合模型對IGS中7個測站實現(xiàn)單站ZTD建模,預測精度達3cm。本文采用中國香港HKSL站數(shù)天的天頂對流層延遲數(shù)據(jù),基于PLS和ELM的理論支持,得到了中國香港地區(qū)單站天頂對流層延遲模型。
1.對流層延遲模型的建立
1.1 偏最小二乘
偏最小二乘法是主成分回歸分析(Principal Component Regression,PCR)的改進。PCR未考慮對輸出變量的解釋能力[4],而PLS在PCR的條件上增加了一個新條件:輸入與輸出應具有盡可能大的相關程度。以下為詳細的推導過程。
已知X和Y分別為n×q和n×p數(shù)據(jù)矩陣(n個樣本點)。首先,用主成分分析對數(shù)據(jù)矩陣X和Y提取最大主成分,數(shù)據(jù)矩陣X和Y分解后得:

上式中,T和R分別是數(shù)據(jù)矩陣Y和X的得分矩陣,V和Q分別為相應的載荷矩陣,E和F分別為數(shù)據(jù)矩陣Y和X的殘差矩陣。之后,建立得分矩陣T和R之間的線性回歸模型:R=BT。由最小二乘原理,可以求得系數(shù)矩陣B的估計矩陣=(T'T)-1T'R。最后,進行數(shù)據(jù)重構(gòu),得到因變量數(shù)據(jù)矩陣X和自變量數(shù)據(jù)矩陣Y之間的關系:

對于標準化輸入變量矩陣Y和輸出變量矩陣,X要求構(gòu)造變量t1和u1滿足:

同時,應滿足以下3個條件:
(1)t1應盡可能大的攜帶輸入變量矩陣X的信息,即Var(t1)→ max。
(2)u1應盡可能大的攜帶輸出變量矩陣Y的信息,即 Var(t2)→ max。
(3)t1和u1應具有的可能大的相關程度,即r(t1,u1)→max。
上述問題可以轉(zhuǎn)化為計算t1和u1的協(xié)方差的最大值,即存在Cov(t1,u1)→max,使得||ω1||=||C1||=1。
構(gòu)造拉格朗日函數(shù),列式求解多元方程,可得矩陣X'YY'X的特征向量為ω1,對應的特征值為θ2。同理,C1使矩陣Y'XX'Y的特征向量,對應的特征值為θ2。
若回歸方程的精度已經(jīng)滿足要求,則停止;否則,利用殘差矩陣X*和Y*,計算第二主成分,并重新建立回歸方程,以此類推,直到回歸方程的精度滿足要求為止。
1.2 極限學習機
從本質(zhì)上說,極限學習機(Extreme Learning Machine,ELM)并不新穎,ELM在神經(jīng)網(wǎng)絡結(jié)構(gòu)上[5],是一個前向神經(jīng)網(wǎng)絡。ELM的輸入層和隱含層的連接權(quán)值可隨機設定,隱含層的閾值也可隨機設定,且隱含層及輸出層之間的連接權(quán)值β無需迭代調(diào)整(通過解方程組確定)。對比傳統(tǒng)的BP神經(jīng)網(wǎng)絡,BP需要不斷反向調(diào)整權(quán)值和閾值,耗費了計算量。
對于單隱含層網(wǎng)絡,假設Xi=[xi1,xi2,…,xim]T∈Rn,ti=[ti1,ti2,…,tim]T∈Rm。對于有L個隱層節(jié)點的單隱層神經(jīng)網(wǎng)絡,可寫為其中,g(x)為激活函數(shù),Wi=[ωi1,ωi2,…,ωim]T為輸入權(quán)重,βi為輸出權(quán)重,bi為第i隱層單元的偏置,Wi·Xj表示W(wǎng)i和Xj的內(nèi)積。
單隱含層神經(jīng)網(wǎng)絡學習的目標是使得輸出的誤差最小,可表示為,即存在 βi,Wi和 bi,使得即 :

其中,H是隱含層節(jié)點的輸出,β為輸出權(quán)重,T為期望輸出。
為了訓練單隱層神經(jīng)網(wǎng)絡,解最小損失函數(shù),即:
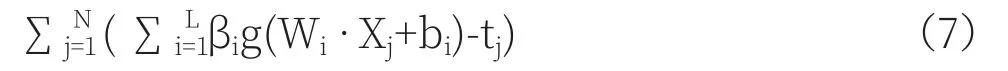
在ELM算法中,一旦輸入權(quán)重Wi和隱層的偏置bi被隨機確定,隱層的輸出矩陣H就被唯一確定。訓練單隱層神經(jīng)網(wǎng)絡可轉(zhuǎn)化為求解一個線性系統(tǒng)Hβ=T的問題。

其中,HT是矩陣H的廣義逆,且可證明求得的解的范數(shù)最小且唯一。
1.3 BP神經(jīng)網(wǎng)絡
BP神經(jīng)網(wǎng)絡又稱為誤差反向傳播神經(jīng)網(wǎng)絡[6],是一種多層前向型神經(jīng)網(wǎng)絡。在BP神經(jīng)網(wǎng)絡中,信號向前傳播,誤差反向傳播。所謂反向傳播是指誤差從最后的輸出層依次向之前各層逐漸進行調(diào)整。由于其在各個領域已得到廣泛應用,且已經(jīng)衍生出了各種基于BP神經(jīng)網(wǎng)絡的改進算法,故原理不再贅述。
1.4 建模思路
在上述的理論基礎上,使用MATLAB R2019a進行算法驗證。對于ZTD文件,輸入為IGS站的位置信息,輸出則為對應時刻的ZTD數(shù)據(jù)。建模時,輸入前一天或者前兩天的位置數(shù)據(jù),輸出為對應ZTD數(shù)據(jù)。測試時,輸入位置信息,輸出預測ZTD數(shù)據(jù)。將預測值與真實值對比,得到精度。最后進行三種方法的精度比較,其中BP神經(jīng)網(wǎng)絡模型為參照組。
2.數(shù)據(jù)來源及分析
本文所用的數(shù)據(jù)來源于中國香港HKSL觀測站,該地區(qū)的經(jīng)度為113.9280°,緯度為22.3720°,高程為95.2757°。本文采用了2019年26日至28日連續(xù)3天的天頂對流層延遲數(shù)據(jù)來進行結(jié)果分析。所使用的HKSL數(shù)據(jù),時間間隔為5min,每天可得到288組數(shù)據(jù)。
3.模型結(jié)果分析
本文以BP神經(jīng)網(wǎng)絡所建立的對流層預測模型為對照組,分析BP對流層預測模型與PLS對流層預測模型和ELM對流層預測模型的精度差異。使用MATLAB完成ZTD文件的數(shù)據(jù)導入,建模,預測,并計算其均方根誤差及平均偏差(本文將IGS所提供的ZTD數(shù)據(jù)作為真值處理)。在建模過程中,考慮了三種不同類型的時間預測(選取三種代表性較強的情況):第1天預測第2天;第1、2天預測第3天:第1天預測第2、3天。得到以下真值偏差圖(綠色為類型1,紅色為類型2,紅色加粉色為類型3)。如圖1所示。

圖1 平均偏差圖
由圖1可知,三種模型的誤差都在20mm以內(nèi)。在精度波動接近時,三種方法的RMSE及Bias有著明顯區(qū)別——BP模型的RMSE最小為8mm,最大為38mm;Bias最小為70mm。而ELM模型及PLS模型的同類指標僅為1mm~2mm,穩(wěn)定性較高。同時有已發(fā)表的論文可知,一般情況下,ELM模型運算速度高于BP模型。
4.結(jié)論
分別使用ELM和PLS建立了對流層延遲預測模型,同時使用BP神經(jīng)網(wǎng)絡預測模型進行對比。結(jié)果表明,ELM模型不僅適于各種時段的對流層延遲預測,而且計算速度快[5],PLS模型則適于短時預報,但精度依舊由于BP神經(jīng)網(wǎng)絡預測模型。一般情況下,ELM模型運算速度高于BP模型。同時ELM模型短時預報及長時預報精度都較高,相比之下,同等精度要求下,PLS模型所需要的建模數(shù)據(jù)更多。

